“數值分析”課程教學中的“分而治之”思想

馬俊杰

貴州大學數學與統計學院 貴州貴陽 550025

一、“數值分析”課程改革的意義與現狀

全國高校思想政治工作會議上強調“要堅持把立德樹人作為中心環節，把思想政治工作貫穿教育教學全過程，實現全程育人、全方位育人，努力開創我國高等教育事業發展新局面”“各門課程都要守好一段渠、種好責任田，使各類課程與思想政治理論課同向同行，形成協調效應”。基于全面育人的課程改革是高等教育面臨的重要問題，也是高等教育發展的必然[1]。“數值分析”作為數學以及理工科專業的重要課程，主要面向高年級本科生以及低年級研究生開設。課程內容一般包含微積分、非線性方程、線性方程組、特征值和特征向量、微分方程初值問題、微分方程邊值問題等，需要高等數學、線性代數、常微分方程等前序課程[2]。因此，“數值分析”的教學內容覆蓋面較大，難度也較高。同時，由于它包含了多門數學類課程，在“數值分析”教學中融入思政教育具有更豐富的內涵，也更有利于學生的全面發展。

“數值分析”課程教學側重數學問題的數值計算方法，是連接計算機與模型問題的重要紐帶，可以培養學生結合抽象思維與實際行動的能力。自上世紀80年代全國高校普遍開設這門課程以來，“數值分析”的課程改革已經取得了許多成績。例如，大量實驗課程的設計以及引入豐富了教學內容，并使得教學過程更加具象，加深了學生對知識點的理解[3]；通過針對專業區分選取教學體系，兼顧了具有不同數學基礎的學生的學習進度[4]；通過引入學科前沿，使得人才培養更加適應社會的發展需求[5]。但是仍需注意的是，“數值分析”教學內容過于煩瑣，在大多數學校這門課程的課時量比較有限，教學過程欠缺“可視化”、課程考核不合理等問題仍是課程教學面臨的重要問題。因此，如何在教學任務緊張、教學內容復雜的情況下融入思想教育實現全面育人是一個重要的課題。

事實上，全面育人與傳統教學內容不是相互排斥的兩個個體，而是相互促進，相輔相成的。以“數值分析”為例，由于課程教學過程中不可避免大量煩瑣的公式推導，學生很容易產生厭學情緒[6]。如果可以合理引入思想教育提高學生的學習積極性，不但有利于課堂教學的開展，而且可以提升教與學的效率。當前“數值分析”課程改革主要關注如何在專業知識的學習過程中融入思政元素，強調學與思的巧妙結合。例如，通過短片向學生介紹使用課程內容解決實際問題的案例，宣傳科技工作者在第一線的感人事跡，增強學生的自豪感；通過結合數學史與數學文化，將我國古代數學的重大成就講授給學生，例如秦九韶算法，進而培養學生的文化自信[7]。但是，“數值分析”課程不僅具有內容豐富的特點，而且包含許多算法構造思想。本文以“分而治之”為落腳點，分析這種思想與辯證唯物主義的關系，培養學生樹立正確的辯證唯物主義和掌握科學的方法論，并總結教學過程中“分而治之”的應用。

二、“分而治之”思想與課程改革思路

“分而治之”思想是算法設計的一種技術，即先將復雜問題分解成數個小問題，針對每個小問題設計算法，進而組裝成原復雜問題的解。這種思想是辯證唯物主義中“具體問題具體分析”這一方法論在算法設計領域的體現。在“數值分析”教學中注重總結算法設計的“分而治之”思想，建立它與辯證唯物主義、建設中國特色社會主義偉大成就的聯系，不僅可以增強學生的愛國熱情，而且可以提高學生對算法設計的認識。在“數值分析”教學中融合算法設計思想需要做到以下幾點。

第一，組建“數值分析”教學團隊，增強教師全面育人意識，提高教師全面育人水平。對于專業課教師，全面育人仍是一個較為陌生的課題。主要原因在于專業課教師在成長過程中將大部分精力都投入科學研究、教材教法等方面，缺乏全面育人教法的培訓。組建教學團隊的優勢是可以通過集體學習的方式使得教師在最短時間成長為全面育人方面的專家。

第二，正確處理課程教學與全面育人的關系。課程教學是教師的主要任務，只有完成大綱要求的教學內容，才能真正實現人才培養的目標。人才的成長應該是全方位的，而不是機械化的，僅僅學習教材中固定知識點的人才不符合當今社會的發展。只有通過全面育人加強學生思維、思想的教育，才能幫助學生成長為社會需要的人才。另外，設計合理的全面育人內容有助于提高學生的學習積極性，提升課程教學效率，進而有效地解決“數值分析”課程內容多、課時少的問題。

第三，創建全面育人平臺，結合線上線下教學夯實全面育人基礎。數學類課程具有教學內容抽象、知識結構嚴謹的特點，對于普通高校的學生，通過自學掌握大綱知識點的難度很大。因此，數學類課程教學改革的重點集中在提高知識傳遞效率、準確性以及借助現代可視化工具將抽象概念具象化。但是，應該注意的是學生通過課下自學的方式達到培養目標仍是十分困難的，而全面育人內容更加貼近生活生產實踐，更加具體，從而更有利于發揮課外學習的優勢。通過建立系統性的線上全面育人材料，結合線下教學內容，可以充分發揮學生的主觀能動性，提高教與學的效率。

第四，發揮先進計算平臺優勢，增強教學內容可視化。建設基于多媒體技術的智慧教室，將Matlab數值實驗案例引入課堂教學，發揮與傳統教學互補的優勢，不僅可以激發學生學習興趣，還可以提升教學效果。例如，在講解最佳多項式逼近問題時，可以借助Matlab中的Chebfun工具箱，實現伯恩斯坦多項式的快速計算。通過講解伯恩斯坦多項式的生成代碼，結合最佳逼近數值結果，可以激發學生的學習興趣，進而為全面育人提供講授空間。

第五，強化數值案例設計，提升學生主觀能動性。“數值分析”作為連接數學模型與實際問題的紐帶，可以提高學生解決實際問題的能力。因此在實驗案例的選取過程中，應該更多地傾向于與實際問題相關的模型，例如德拜溫度模型、棒球運動軌道模型、光學散射積分問題、化學熱反應模型、傳染病模型等。模型的合理選擇可以使學生產生對“數值分析”教學內容的興趣。通過對實驗教學環節的重視，可以加深學生對課堂教學內容的理解，為“數值分析”全面育人提供了肥沃的土壤。

三、“分而治之”思想教學總結

拉格朗日插值既是數值逼近的重要內容，也是數值積分、數值微分、微分方程數值等的基礎[8]。一般地，對于插值節點x0…xn以及函數值y0…yn，可以找到不超過n次的多項式pn(x)使得pn(xi)=yi,j=0…n。在實際應用中，插值節點一般選取為等距節點。對于函數f(x)=sin(x)，分別取n=5和n=50，可以計算如圖1中的插值多項式。從圖中看出當插值節點增加時，拉格朗日插值函數對原函數的逼近效果是變好的。

圖1 拉格朗日插值法的逼近效果，原函數為f(x)=sin(x)

但是，當原函數變為Runge函數時，重復同樣的實驗結果大不相同(見圖2)。通過實驗結果的對比，可以使得學生更加具體地理解拉格朗日插值法的局限性。

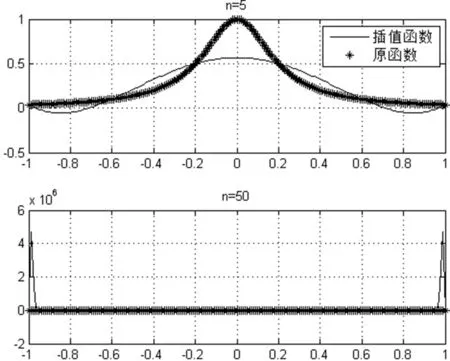
圖2 拉格朗日插值法的逼近效果，原函數為龍格函數

任何算法的設計都是在已有方法的基礎上針對實際計算中遇到的問題不斷完善而得到的。在遇到拉格朗日插值法無法逼近龍格函數這一問題時，可以適時地引入“分而治之”思想，并結合唯物辯證法中的“具體問題具體分析”對學生進行講解。具體到本案例，“分而治之”即將原區間上的插值問題分割成小區間上的插值問題。在小區間上，可以僅僅使用低次插值，例如線性插值，然后將所有低次插值函數連接成大區間上的插值函數，即得到圖3。可以看出，將拉格朗日插值結合“分而治之”思想可以很恰當地解決龍格函數的插值問題。

圖3 拉格朗日插值法結合“分而治之”思想的逼近效果，原函數為龍格函數

在定積分的數值計算中，也常使用“分而治之”思想。牛頓—科特斯公式是計算數值積分的常用工具[9]。考慮使用梯形公式計算定積分:

利用Matlab可得它的近似值為0.099916708323414，它的真實值是0.099944461108277，絕對誤差僅僅為0.000028。所以梯形公式的計算結果是十分精確的。當積分區間延長為[0，1]時，使用梯形公式可得近似值為0.092073549240395，它的真實值是0.946083070367183，絕對誤差為0.85401。所以梯形公式的計算結果是不可靠的。在此可引入“分而治之”思想，先將區間[0，1]劃分為10個小區間[0，0.1]，[0.1，0.2]，[0.2，0.3]，[0.3，0.4]，[0.4，0.5]，[0.5，0.6]，[0.6，0.7]，[0.7，0.8]，[0.8，0.9]，[0.9，1]。對每個小區間使用梯形公式，然后利用積分的可加性將計算結果組合在一起即可得到。相應計算結果為0.945832071866905，絕對誤差為0.00025。計算精度比直接使用梯形公式提高了很多，也體現了“分而治之”思想的優越性。

“分而治之”思想在矩陣特征值計算、稀疏線性系統的快速求解、常微分方程初值問題數值解等方面也有重要應用，在遇到復雜系統或者多尺度問題時，根據問題的不同部分的不同性質設計針對性的算法，是解決實際問題的重要技術。

結語

“分而治之”思想是數值算法設計的重要技術，由這一思想引出大量經典數值方法，例如分段低次多項式插值、三次樣條函數插值、復化牛頓—科特斯公式等[10-12]。在“數值分析”的教學實踐中，注重總結算法設計思想并將其融入課堂教學，不僅可以提高教學效率，而且有助于實現全面育人的目標。