數學建模案例融入線性代數教學的探索
李燕娟 王芬琴
蘭州博文科技學院 甘肅蘭州 730101
1 概述
線性代數課程是理工類專業必修的一門專業基礎課,它在工程技術等領域有著廣泛的應用,并且在培養學生邏輯思維能力方面起著非常重要的作用。但是線性代數教學目前仍然存在以下問題:第一,著重理論教學,晦澀難懂,導致學生學習主動性不強;第二,與實際問題聯系較少,不利于學生數學應用能力的培養。因此,線性代數教學改革迫在眉睫。
數學建模是根據實際問題用數學語言轉換為數學問題,進而分析問題,建立模型,然后運用數學知識對模型求解,最后根據計算結果來解決實際問題的過程[1]。線性代數中有許多概念抽象難懂,學生聽得云里霧中,掌握不牢固,更是覺得學習相關知識沒有什么用。所以,在講解概念的過程中引入數學模型,有助于對概念的深入理解,起到事半功倍的作用[2]。將數學建模思想融入線性代數教學過程中,理論聯系實際,不僅活躍課堂氣氛,調動學生學習積極性,而且利用數學模型,變抽象為具體,有利于培養學生的數學應用能力。下面通過引入數學模型來詮釋線性代數中矩陣的定義、矩陣相乘、矩陣的逆等知識點。
2 數學建模案例研究
例1[3]:某航空公司在A、B、C、D共4個城市之間開通若干條航線,這4個城市間的航班通行情況如下圖所示。若有航班通行用“1”表示,無航班通行用“0”表示,則根據這4個城市之間的通行情況建立如下表1。問題:中轉一次可以使C城市和D城市之間通航嗎?
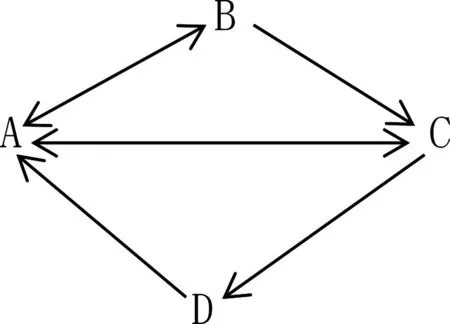

表1
分析:用圖表示通行情況存在一定的弊端,比如當城市無限增多時,圖形看起來很復雜。而換用表格表示,則只需增加相應行和列即可,此時恰好引入矩陣的概念,并利用表格說明矩陣的特點,矩陣是個數表,而且數表里面的元素不能隨意變換位置。例1用矩陣就可以表示為:
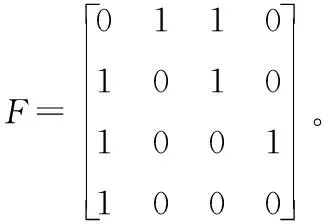
解:城市ABCD用數字1234表示,矩陣F中的元素fij等于1表示兩個城市之間可以通航,等于0表示兩個城市之間不能通航。則圖或者表格可以表示為矩陣F,下面求中轉一次兩個城市之間的通行情況:
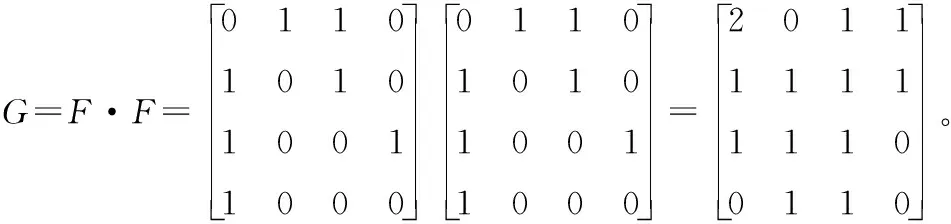
矩陣G中的元素gij表示從城市i到城市j中轉一次的路線條數,b34=0表示從城市C到城市D中轉一次不能通航;b43=1表示從城市D到城市C中轉一次只有1條路線,D→A→C。
例2:線性代數課程的綜合成績是由考勤、提問、作業和末考構成的,分別占比10%、10%、20%和60%。已知甲、乙、丙、丁四名同學考勤、提問、作業、末考成績如下表2所示,問題:四名同學成績從高到低的順序是什么?
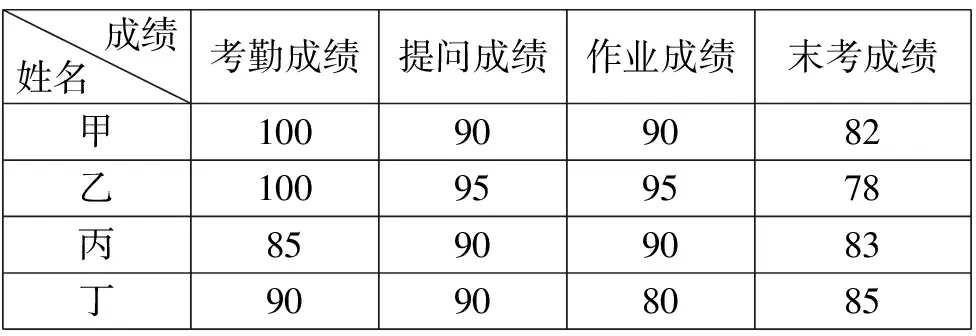
表2
分析:將甲、乙、丙、丁四名同學的每項成績乘以相應比例可得綜合成績,可以寫出兩個矩陣,第一個矩陣行表示四名同學,列表示各項成績,第二個矩陣只有一列表示各項成績占比,最后再相乘。
解:由題意可設以下兩個矩陣:

由矩陣相乘可得:

C即為四名同學的綜合成績,從結果易得:第一名是甲,第二名是乙和丙,第三名是丁。
計算過程可借助Matlab軟件,編寫程序:
A=[100 90 90 82;100 95 95 78;85 90 90 83;90 90 80 85];
B=[0.1;0.1;0.2;0.6];
C=A*B
按Enter鍵,就可得結果為:
C=
86.2000
85.3000
85.3000
85.0000
從這個例題可以看出,末考成績第一名其綜合成績并不是第一名,末考成績最后一名其綜合成績是第二名,此時教育學生不要只為考試而學習,要注重平時學習的重要性,學習是持續性的,不是一蹴而就的。
例3:為確保傳遞信息的保密性,往往會對傳輸信息進行加密再解密,可得知傳遞的原信息。例如,若要傳遞信息stop,我們可采取26個英文字母與數字對應的加密法。假設26個英文字母與數字之間建立一一對應關系
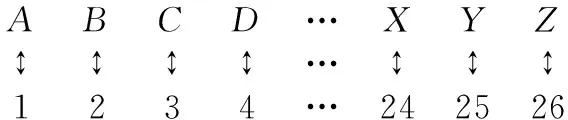

分析:已知C=AB,求B,首先求A-1,再求B=A-1C,根據字母與數字的對應關系,就可以知道原傳輸信息內容。
解:根據伴隨方陣法或者初等變換法求A-1,
方法一:伴隨方陣法
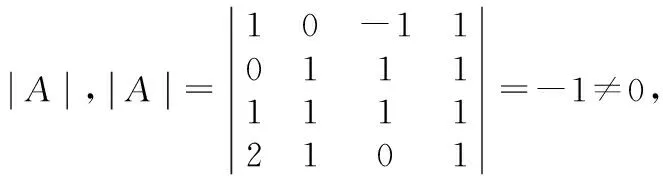
A11=0,A21=1,A31=-1,A41=0,A12=1,A22=-2,A32=3,A42=-2,A13=0,A23=1,A33=-2,A43=1,A14=-1,A24=0,A34=-1,A44=1,
方法二:初等變換法
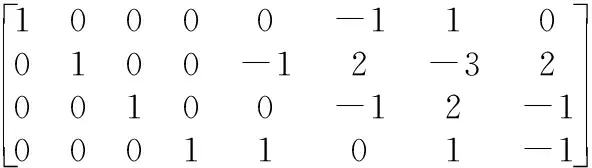
所以:
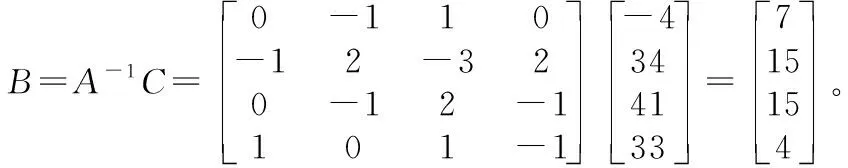
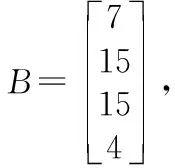
根據字母與數字的對應關系,7,15,15,4對應的字母為g,o,o,d,可得原傳輸信息為good,以上為解密過程。
利用Matlab軟件可求A-1和B,程序為:
A=[1 0 -1 1;0 1 1 1;1 1 1 1;2 1 0 1];
inv(A)
ans=
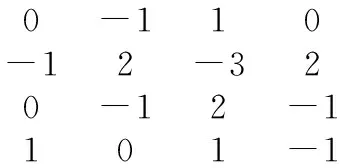
B=[0 -1 1 0;-1 2 -3 2;0 -1 2 -1;1 0 1 -1]*[-4;34;41;33]
B=
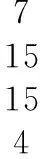
結語
在線性代數教學過程中融入數學建模案例,使知識變得直觀化、具體化,通過實際問題和數學聯系起來,使學生更容易接受新知識,將實際問題轉換為數學問題來解決,從而提高學生分析問題、解決問題的能力。在數學建模案例選取過程中,需要注意以下幾點:(1)根據學生的接受能力選取適當的案例,不易太難。(2)根據學生的專業選取合適的案例,使學生能夠將數學知識融入專業知識中,使后續的專業課學習更加得心應手。那么,如何有效地將數學建模思想融入線性代數課程的教學過程中,這是一個長期的、需要不斷探索的、潛移默化的過程。因此,應逐步將數學建模與線性代數教學有機結合,將學與用有機結合,將專業基礎知識教育與培養學生綜合素質、創新能力、應用能力有機結合[4],這對培養應用型人才具有很大的促進作用。

