不同激素種類?濃度和插穗年限對吳茱萸扦插育苗的影響
毛明輝 黃意成 曾慶錢 杜長江 鄭海


摘要 [目的]研究中藥材吳茱萸扦插生根的最適宜條件。[方法]采用3因素3水平正交試驗設計,用愈傷組織形成率、發芽率、生根率、根數和根長為生根參考指標,探討插穗年份、萘乙酸(NAA)和吲哚丁酸(IBA)對吳茱萸扦插生根效果的影響。[結果]影響吳茱萸扦插生根最主要的因素是植物生長調節劑種類,其次是調節劑濃度,插穗年限的影響最小。極差分析和主成分分析發現,扦插生根綜合效果指標最適合的因素組合是IBA 200 mg/L、扦插年限1年,生根指標最好,即愈傷組織形成率達76.13%,發芽率達75.90%,生根率78.16%,生根數5.09條,平均根長4.75 cm。[結論]在大批量生產中建議采用1年生插條,然后用200 mg/L IBA進行插穗處理,可提高出苗率,并且能夠保證成苗品質穩定。
關鍵詞 吳茱萸;植物生長調節劑;種類;濃度;插穗年限;扦插育苗
中圖分類號 S 567.1+9? 文獻標識碼 A? 文章編號 0517-6611(2022)03-0102-04
doi:10.3969/j.issn.0517-6611.2022.03.026
Effects of Different Hormone Types,Concentrations and Cutting Years on Cutting Seedlings of Evodia rutaecarpa
MAO Ming-hui1, HUANG Yi-cheng1,2,3, ZENG Qing-qian1 et al
(1.Guangdong Institute of Traditional Chinese Medicine, Guangzhou,Guangdong 510520;2.China Academy of Chinese Medical Sciences, Beijing 100700;3.Guangdong Food and Drug Vocational College, Guangzhou,Guangdong 510520)
Abstract [Objective]To study the optimum conditions for cutting rooting of Chinese medicinal material Evodia rutaecarpa.[Method]A three-factor and three-level orthogonal test design was adopted, and callus formation rate, germination rate, rooting rate, root number and root length were used as reference indicators for rooting to explore the effects of cutting years, naphthylacetic acid (NAA) and indolebutyric acid (IBA) on the rooting effect of Evodia rutaecarpa cuttings.[Result]The most important factor that affected the rooting of Evodia rutaecarpa cuttings was the type of plant growth regulator, followed by the regulator concentration, and the cutting years had the least influence.Range analysis and principal component analysis found that the most suitable factor combination for the comprehensive effect index of cutting rooting was IBA 200 mg/L, cutting year was 1 year, and the rooting index was the best, that was, the callus formation rate was 76.13%, the germination rate was 75.90%, the rooting rate was 78.16%, the root number was 5.09, and the average root length was 4.75 cm.[Conclusion]In mass production, it is recommended to use 1-year-old cuttings, and then use 200 mg/L IBA for cuttings treatment, which can increase the emergence rate and ensure the stable quality of seedlings.
Key words Evodia rutaecarpa;Plant growth regulator;Types;Concentration;Cutting years;Cutting seedlings
基金項目 中央本級財政項目“名貴中藥資源可持續利用能力建設”(2060302-1702-15);2020年廣東省科技專項資金項目“粵北山區道地南藥生態種植技術研究與示范”(200831086270718);2018年中醫藥公共衛生服務補助專項“全國中藥資源普查項目”(財社〔2018〕43號);廣東食品藥品職業學院項目“雙高計劃打造技術技能創新服務平臺”(SG03-02.5);2020年省科技專項資金項目“省級農村科技特派員重點派駐任務”。
作者簡介 毛明輝(1972—),女,湖南岳陽人,農藝師,碩士,從事中藥組織培養技術與規范化栽培研究。通信作者,主管中藥師,從事中藥鑒定和中藥材規范化栽培研究。
收稿日期 2021-04-28;修回日期 2021-07-01
吳茱萸別名吳萸、茶辣、漆辣子、臭辣子等,為蕓香科植物吳茱萸[Evodia rutaecarpa(Juss.)Benth.]的干燥近成熟果實,是配方中常使用的中藥材,其性熱味苦辛,具有散寒止痛、降逆止嘔、助陽止瀉等功效,用于治療厥陰頭痛、寒疝腹痛、寒濕腳氣、脘腹脹痛、嘔吐吞酸、五更泄瀉、外治口瘡、高血壓等癥[1]。研究表明吳茱萸主要化學成分包括生物堿、苦味素、黃酮和揮發油等[2]。吳茱萸堿具有抗腫瘤、抗傷害感受、減肥、保護心臟、降血壓等藥理學活性[3]。吳茱萸次堿具有保護心臟、擴血管、降壓、松弛肛門內括約肌、抑制胃腸運動、抑制血小板聚集和動脈血栓形成、抗炎、鎮痛、抗腫瘤等藥理作用[3-4]。吳茱萸分布范圍廣、變種繁多,主要以栽培資源供應市場,重慶、貴州、湖南、江西等地為其主產區[5],石虎品種主要栽培于貴州省銅仁市,湖南省新晃縣、婁底市、瀏陽等地;吳茱萸品種主要栽培于湖南省湘鄉、瀏陽,江西省萬載,浙江省建德、平陽等地;疏毛吳茱萸品種主要栽培于廣西柳城、陽朔,貴州省余慶、松桃,江西省樟樹等地[6]。由于吳茱萸種子萌發率低下,且種子苗生長緩慢,因此扦插苗是批量生產吳茱萸種苗的重要苗源。史艷財等[7-10]采用多種人工合成激素對吳茱萸插條進行處理獲得吳茱萸種苗,并取得階段性效果,但扦插成苗率尚不是很高。該研究采用不同濃度的萘乙酸(NAA)、吲哚丁酸(IBA)、萘乙酸和吲哚丁酸等比例混合使用對吳茱萸進行扦插生根的試驗,提高吳茱萸扦插成苗率,為吳茱萸種苗大規模繁殖提供技術支持。
1 材料與方法
1.1 試驗場地準備與處理
廣東省翁源縣恒之源農林科技有限公司于2018年開始分批次在韶關市翁源縣種植近133.3 hm2吳茱萸,該試驗于2020年12月—2021年4月在該公司溫室小拱棚內進行。選用當地疏松紅壤土作為育苗苗床,清表后起壟使苗床長約20 m、寬1.5 m、高30 cm,并于扦插前1 d對育苗床進行噴灑滅菌消毒,可用高錳酸鉀溶液(質量濃度為0.3%)或多菌靈可濕性粉劑(活性成分50%的1 g多菌靈粉劑用800~1 000 L水配制成溶液)。
1.2 材料的準備與處理
提前于2018年12月、2019年12月、2020年6月對廣東省翁源縣恒之源農林科技有限公司種植多年的吳茱萸母株進行截干以促使新萌芽枝生長。試驗要求使用健康、大小一致、無病蟲害的枝條,用枝剪剪成長約100 cm的枝條后立即帶回陰涼處進行短枝剪枝以減少水分喪失。剪成的插條要求帶2~3個莖節、底部無葉、頂端留約2片葉、上切口為平切口、下切口為斜切口,剪好的插條用橡皮筋綁成50枝一把,并立即用消毒劑浸泡插條穗基部10 min消毒。消毒后再按試驗設計方案用不同的植物生長調節劑浸泡插條基部時間1 h。
1.3 試驗設置與處理
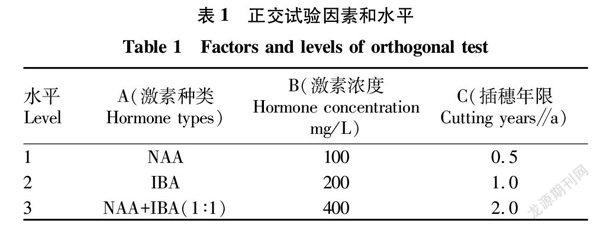
以激素種類、激素濃度和插穗年限為試驗影響因素,以當地紅壤土為扦插育苗基質,以清水處理作為對照,采用3因素3水平正交試驗設計(表1),試驗共設置10個處理,每個處理100根穗條并重復3次,采用隨機區組設計。
1.4 扦插方法
把插條長度50%以上插入苗床中,并能緊密固定插條。全部插條扦插完成后澆一次透水,用塑料薄膜遮蓋小拱棚并用遮陽網控制育苗床80%的遮陽率。
1.5 扦插后管理
扦插后為避免枝條過度蒸發失水死亡,如遇晴朗天氣每天最少澆5次水,每間隔2~3 h澆一次,之后可減少澆水頻率,早晚各澆一次即可,如遇陰雨天可不澆,保持溫室大棚內溫度20~30 ℃,相對空氣濕度90%左右。扦插后每隔7 d左右噴灑一次1 000倍百菌清和多菌靈殺菌劑,2種殺菌劑交替使用,輪流時間為7 d,以避免插條在高溫高濕條件下感染雜菌,提高成苗率。
1.6 煉苗與出圃
由于種苗繁育在小拱棚內進行,整個培育過程的各種環境都是人工調控的,這樣的種苗脆嫩,不利于運輸和移植,如果直接移植到大自然環境中,則會因為種苗對生長環境無法適應而死亡。因此種苗在出圃前必須在降濕、降溫、增光、增加通風量的條件中煉苗7~14 d。
1.7 數據統計分析
扦插90 d后對試驗結果進行統計,20 d后統計植物的發芽率;插后30 d隨機抽取20~30株,查看愈傷組織形成狀況;90 d后取出進行生根效果觀察,統計其平均生根條數、平均根長、生根率等生根技術指標。愈傷組織形成率=(形成愈傷組織的插條數量/插條總數量)×100%;發芽率=(發芽的插條數量/插條總數量)×100%;生根率=(生根插條數量/插條總數)×100%;平均生根數量=20根插條總生根數量/20;每個試驗處理取20根生根插條,計算根長并取平均值。通過Excel和SPSS 13.0軟件對試驗數據進行分析。
2 結果與分析
2.1 扦插生根情況
2.1.1
扦插生根過程。根據對吳茱萸扦插生長的整個過程進行觀察,其生根過程可分為4個階段:①新芽萌發階段(0~20 d),新芽開始萌發(圖1A),愈傷組織尚未形成(圖1B);②愈傷組織形成階段,20 d后切口膨大,誘導愈傷組織的生成(圖1C);③不定根形成階段,超過60 d,扦插基部出現不定根(圖1D);④不定根增加階段,80 d后,不定根大量增多(圖1E)。吳茱萸整體生長情況如圖1F、G、H所示。
2.1.2
不同處理吳茱萸生根效果統計。扦插90 d后對試驗結果進行統計,統計結果如表2所示。試驗結果顯示,處理⑤的各項試驗結果指標均為最高,分別為愈傷組織形成率76.13%、發芽率75.90%、生根率78.16%、生根數5.09條、根長4.75 cm。
2.2 不同處理對吳茱萸扦插生根效果的極差分析
2.2.1
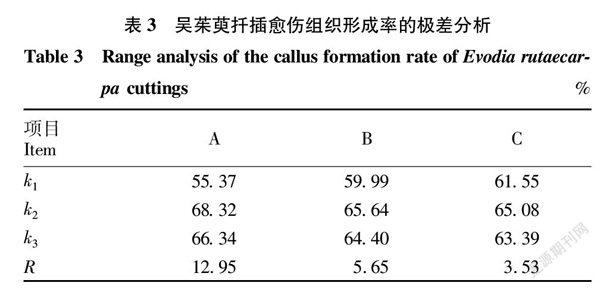
各處理對吳茱萸扦插30 d后愈傷組織形成情況的極差分析。試驗結果表明(表3),不同激素、同一激素不同濃度水平及插穗年限對插穗愈傷組織形成差異明顯。各因素對愈傷組織形成率影響的大小排序為A>B>C,表明激素種類對愈傷組織形成率的影響最大,激素濃度次之,插穗年限影響最小;優化水平組合為A2B2C2,愈傷組織形成率最高為76.13%。
2.2.2
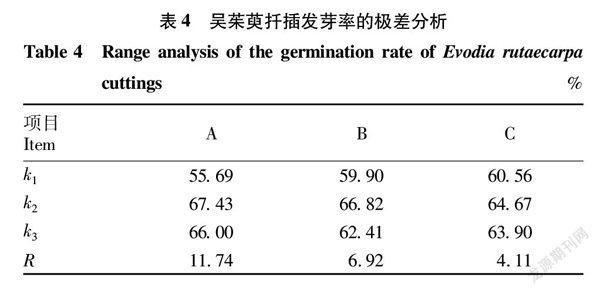
各處理對吳茱萸扦插20 d后發芽率情況的極差分析。試驗結果表明(表4),各因素對發芽率影響的大小排序為A>B>C,表明激素種類對發芽率的影響最大,激素濃度次之,插穗年限影響最小;優化水平組合為A2B2C2,發芽率最高達75.90%。
2.2.3
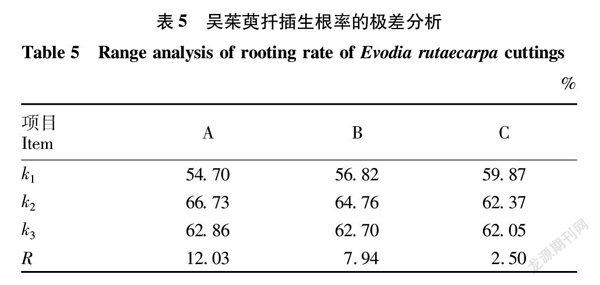
各處理對吳茱萸扦插90 d后生根率的極差分析。由表5可知,各因素對生根率影響的大小排序為A>B>C,表明激素種類對生根率的影響最大,激素濃度次之,插穗年限影響最小;優化水平組合為A2B2C2,最高生根率為78.16%。
2.2.4
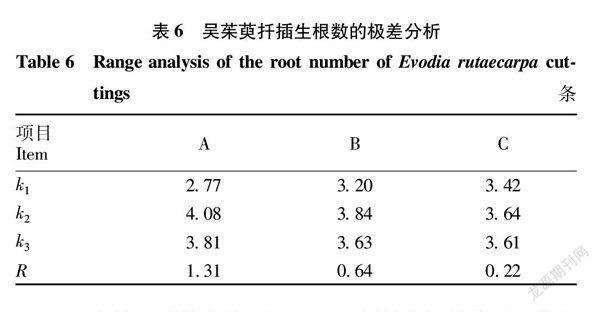
各處理對吳茱萸扦插90 d后生根數的極差分析。由表6可知,3個因素對生根數影響的大小排序為A>B>C,表明激素種類對生根數的影響最大,激素濃度次之,插穗年限影響最小;優化水平組合為A2B2C2,最多生根數達5.09條,最少生根數2.63條,高出2.46條。
2.2.5
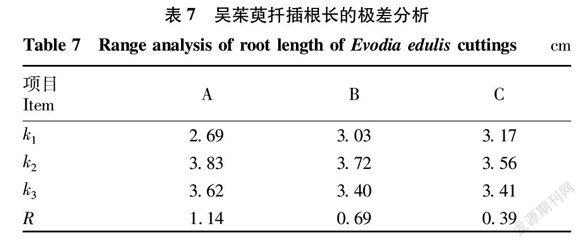
各處理對吳茱萸扦插90 d后根長的極差分析。由表7可知,各因素對根長影響的大小排序為A>B>C,表明激素種類對根長的影響最大,激素濃度次之,插穗年限影響最小;優化水平組合為A2B2C2,最長根長達4.75 cm,最短根長為2.68 cm,相差2.07 cm。
2.3 主成分分析
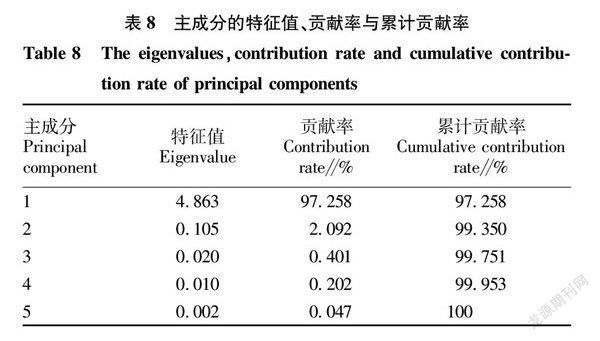
為了從整體上評價吳茱萸扦插生根效果,對愈傷組織形成率(X1)、發芽率(X2)、生根率(X3)、生根數(X4)、根長(X5)5個指標進行主成分分析,結果發現(表8),第1和第2主成分的累計貢獻率為99.350%,其中第1主成分的貢獻率為97.258%,根據累計貢獻率>75%的原則和系統默認方差>1的為主成分提取主成分,可知信息主要集中在第1個主成分中,所以選取第1個主成分來表達吳茱萸扦插生根綜合效果的信息量。
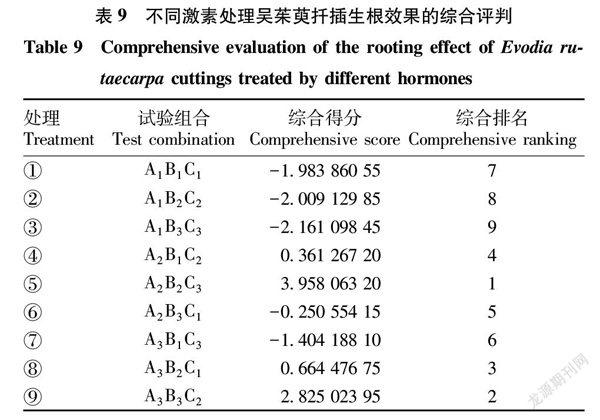
對主成分1進行載荷矩陣計算,最終得出第1主成分的函數表達式為Y1=0.450X1+0.442X2+0.442X3+0.450X4+0.451X5。以Y1主成分與其貢獻率(表8)構建吳茱萸扦插生根效果指標綜合評價模型Z,Z是主成分Y1的線性組合,即為Z=0.972 58Y1,利用該表達式對插穗5個生根指標進行綜合評價,結果見表9。
由表9可知,正交試驗處理⑤排名第一,即A2B2C3組合扦插綜合生根效果指標最好,這與愈傷組織形成、發芽率、生根率、生根數和根長指標極差分析中最佳組合研究結果(A2B2C2)基本一致,即最佳激素種類和濃度一致,插穗年限不一致,分析其主要原因是正交試驗組合表(表2)中無A2B2C2組合。對于扦插生根來說,插穗一般半木質化枝條最為適宜,而吳茱萸根1年生枝條為半木質化,這與極差分析結果相一致,即選擇A2B2C2組合扦插生根綜合指標最為適宜。排名第二為處理⑨即A3B3C2組合,排名靠后的是處理③即A1B3C3和處理②即A1B2C2,說明這2個處理生根綜合效果指標較差。從主成分分析法可以看出,吳茱萸最適合的植物生長調節劑是吲哚丁酸(IBA)。
3 結論與討論
扦插苗育苗成敗的關鍵在于插條能否快速形成愈傷組織并長出根系,只有愈傷組織形成并生根后才能更好吸收水分和養分,促進葉片生長和光合作用,從而形成良性循環。
植物莖枝木質化程度隨著生長年份的延長而增高,抗逆性增加,再生能力減弱,使插條的適應過程和根系的萌發時間延長。在扦插育苗時,特別是對很難生根的藥用植物,一定要采取母樹截干等手段誘導萌芽枝。在該試驗中,母樹截干后萌發的1年生插條生根效果最佳。
研究表明,外源植物生長調節劑能夠促進插條產生不定根,也可使難以扦插生根的植物生根,不同種類的外源生長調節劑對不定根的促進作用不同[11-15],使用合適的植物生長調節劑能通過調節生理機能對多數植物插條顯著提高生根效果[16],包括重新分配插條內部營養物質,增加含糖量和酶活性,刺激細胞分裂和細胞伸長的形成[17],達到使插條快速生根和生長的目的,但種類和濃度要掌握好,種類和濃度不合適都容易抑制插條生根,因此在大批量扦插育苗時,要先進行相關試驗。該試驗結果表明,吳茱萸扦插育苗應使用植物生長調節劑。以吲哚丁酸為植物生長調節劑,使用200 mg/L激素濃度,1年生枝條插條生根效果最好。
參考文獻
[1] 國家藥典委員會.中華人民共和國藥典:2015年版一部[S].北京:中國醫藥科技出版社,2015:171.
[2] 高振雷.吳茱萸化學成分及藥理作用研究概況[J].科學技術創新,2020(13):53-54.
[3] 胡長平,李元建.吳茱萸堿和吳茱萸次堿的藥理學研究進展[J].中國藥理學通報,2003,19(10):1084-1087.
[4] 劉東梅,楊云云,杜俊潮,等.吳茱萸堿的體外抗腫瘤活性研究[J].化學與生物工程,2014,31(7):16-18,26.
[5] 魏寶陽.中藥吳茱萸道地性形成相關因子的研究[D].長沙:湖南農業大學,2012.
[6] 高國賦,魏寶陽,李順祥,等.吳茱萸主栽品種及資源分布現狀[J].湖南中醫雜志,2015,31(7):154-156.
[7] 史艷財,鄒蓉,孔德鑫,等.吳茱萸扦插繁殖技術研究[J].北方園藝,2012(2):181-183.
[8] 楊再學,李大慶,文西明.速效生根靈浸泡時間對吳茱萸扦插出苗的影響[J].山地農業生物學報,2004,23(4):313-314,320.
[9] 萬自成,徐云龍,錢國明.吳茱萸扦插苗繁育技術規程[J].現代園藝,2016(13):78-79.
[10] 吳玉華.吳茱萸扦插育苗技術[J].低碳世界,2019,9(2):323-324.
[11] 楊慶春,李國雷.不同植物生長調節劑對栓皮櫟嫩枝扦插的影響[J].東北林業大學學報,2017,45(6):12-16,46.
[12] 張玉臣,周再知,梁坤南,等.不同植物生長調節劑對白木香扦插生根的影響[J].林業科學研究,2010,23(2):278-282.
[13] 胡勐鴻,歐陽芳群,賈子瑞,等.歐洲云杉扦插生根影響因子研究與生根力優良單株選擇[J].林業科學,2014,50(2):42-49.
[14] 陳慶生,周鵬,張敏,等.激素和插穗處理對烏飯樹扦插生根的影響[J].東北林業大學學報,2016,44(4):41-43,47.
[15] 陳蘭海,唐明亮,孫曉慧,等.基質·激素及其濃度對榛子嫩枝扦插生根的影響[J].安徽農業科學,2021,49(18):129-131,134.
[16] 詹亞光,楊傳平,金貞福,等.白樺插穗生根的內源激素和營養物質[J].東北林業大學學報,2001,29(4):1-4.
[17] 鄭健,鄭勇奇,苑林,等.金露梅扦插繁殖技術研究[J].林業科學研究,2007,20(5):736-738.

