精準設計題目 提升課堂效率
——以數列分奇偶項求和的高三復習課為例
?福建省廈門雙十中學漳州校區
陳 悅
1 引言
數列分奇偶項求和是一個比較難的問題,學生往往不能根據數列通項公式的特點,選擇合適的求和方法來解決問題.高三的復習課是比較緊湊的,帶有明確的目標.本節課主要探討數列分奇偶項求和的四種類型:(1)相隔一項成等差數列(或成等比數列);(2)通項公式中含有(-1)n;(3)數列的通項公式以分段數列給出;(4)數列中連續兩項和的問題.
復習課與習題課是兩種截然不同的的課型,復習課主要是以講解習題為載體,鞏固知識和方法,并發展能力,與新授課不同[1].教學設計主要包括了以下五個環節:回顧知識要點、分析例題、反饋練習、鞏固提高以及歸納總結.
2 確定教學目標
第一,通過知識回顧、例題講解、反饋訓練、鞏固提高等一系列教學活動,讓學生能夠基本掌握常見的數列分奇偶項求和的方法.例如,分組求和法和并項求和法.第二,數列分奇偶項的求和問題也會和其他求和方法相結合,要引導學生根據不同的題目條件,選擇最優解決問題的方法.第三,要引導學生進行數學表達,由特殊到一般,要善于歸納總結,不僅要能想出來、說出來,還要能準確規范地用數學語言表達出來.第四,促進學生思維的發散,比如相隔一項成等差數列可以轉化為分奇偶項求和的問題,那么如果是相隔兩項成等差數列呢?當然,最主要的是在教學各個環節滲透化歸與轉化以及分類討論等數學思想方法,培養學生的探究精神以及分析解決問題的能力,提升學生的數學抽象、數學運算、邏輯推理等核心素養.
3 教學實施過程
第一環節:知識回顧.

設計意圖:復習本節課要用到的知識,以及數列分奇偶的常見類型.
第二環節:例題講解.
例1(2004年北京理第14題)定義“等和數列”:在一個數列中,如果每一項與它的后一項的和都為同一個常數,那么這個數列叫做等和數列,這個常數叫做該數列的公和.已知數列{an}是等和數列,且a1=2,公和為5,那么a18的值為;這個數列的前n項和Sn的計算公式為.
思路分析:根據數列的定義,可以得到an+an+1=5,把a1=2代入,容易發現,奇數項的值都為2,偶數項的值都為3,所以a18=3.第二空要求數列的前n項和,需要對n進行分類討論.
師:好,那數列{an}的通項公式要如何表達?
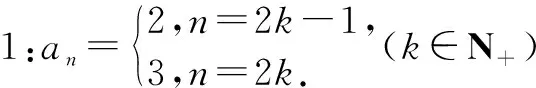
當n為奇數時,
Sn=a1+a2+……+an-1+an
=(a1+a3+……+an)+(a2+a4+……+an-1)
當n為偶數時,
Sn=a1+a2+……+an-1+an
=(a1+a3+……+an-1)+(a2+a4+……+an)

例2(2022年漳州市二質檢第8題)已知Sn是數列{an}的前n項和,a1=1,a2=2,a3=3,記bn=an+an+1+an+2,且bn+1-bn=2,求S31.
解析:由bn+1-bn=2,得an+3-an=2.發現數列{an}相隔兩項依次構成等差數列.
當n=3k-2時,an=a3k-2=1+2×(k-1)=2k-1,k∈N+;
當n=3k-1時,an=a3k-1=2+2×(k-1)=2k,k∈N+;
當n=3k時,an=a3k=3+2×(k-1)=2k+1,k∈N+.
所以,數列{an}的通項公式:
這時候就可以求S31.
設計意圖:例1是相隔一項成等差數列的問題,例2遷移到相隔兩項成等差數列,培養學生的應用意識和發散思維.
例3已知數列{an}的前n項和Sn滿足Sn=2n+1-2(n∈N+).
(1)求數列{an}的通項公式;
(2)已知bn=(-1)nlog2a2n+1,求數列{bn}的前n項和Tn.
思路分析:第(1)問比較容易,可以利用an=Sn-Sn-1(n≥2),解得an=2n.第(2)問,把an=2n代入得到bn=(-1)n(2n+1),再對數列求和.
師:同學們,接下來,怎么處理?
生2:分組求和.對n進行分類討論.
當n為奇數時,

當n為偶數時,


生3:還可以用并項求和法.下面以n為奇數為例.
當n為奇數時,Tn=(b1+b2)+(b3+b4)+……+(bn-2+bn-1)+bn.
師:如果我們留下的是首項,可不可以?
Tn=-3+(5-7)+(9-11)+……+(2n-1-2n-1)
最后的結果也正確,相比較而言,留首項會比留末項好一些,特別是當末項不容易化簡的時候.
設計意圖:復習數列分奇偶項求和的兩種常見方法,即分組求和法與并項求和法.如果運用并項求和法,討論n為奇數時,要考慮剩下的一項,不要遺漏,建議留下首項.如果求和結果是分奇偶的,要記得用分段數列形式表示.
第三環節:反饋訓練.
變式1已知cn=(-1)n·2n,求數列{cn}的前n項和Sn.
師:這個題目,大家可以先對n分奇偶,再分組求和或者并項求和,做法如下:
當n為奇數時,
Sn=-(2+23+……+2n)+(22+24+……+2n-1)
當n為偶數時,

其實,我們也可以把數列{cn}整理成cn=(-2)n,直接代入等比數列的前n項和公式中,得到
Sn=(-2)+(-2)2+(-2)3+……+(-2)n
師:特別注意,如果cn=(-1)n-1·22n+1怎么辦?
學生思考,討論.
師:把{cn}變為cn=8·(-4)n-1(n∈N+)即可.
師:如果把題目變成cn=cosnπ·2n-1(n∈N+),那怎么處理?
生4:cn=cosnπ·2n-1看成cn=(-1)n·2n-1.
師:是的,非常正確.
設計意圖:設置這個題,讓學生感受數列分奇偶項求和與等比數列相結合時,可以選擇分奇偶,用分組求和或者是并項求和,當然也可以轉化為等比數列求和,比較簡潔.注意引導學生將題目條件等價轉化為熟悉的情境進行求解.
第四環節:鞏固提升.
變式2已知cn=(-1)n·n·2n,求數列{cn}的前n項和Sn.
思路分析:設置這個題,讓學生感受數列分奇偶項求和與等差乘以等比數列相結合時,要盡量轉化為等比數列求和,比較簡便.
師:有同學能解決這個問題的嗎?
生6:把(-1)n·2n看成(-2)n,利用錯位相減法.
Sn=1×(-2)1+2×(-2)2+……+n×(-2)n
①
-2Sn=1×(-2)2+2×(-2)3+……+n×(-2)n+1
②
由①-②,可得
3Sn=1×(-2)1+1×(-2)2+1×(-2)3+……+1×(-2)n-n×(-2)n+1.



師:這個題目要求{cn}的前2n項和S2n,就不用對n進行分類討論了.
由題意可得,
S2n=c1+c2+……+c2n-1+c2n
=(2+23+……+22n-1)+(32+34+……+32n)
驗證當n=1時,S2=11=c1+c2,符合題意.

4 結語
“好的例題教學就是照亮學生解題的燈塔.”那么一名好教師,就是自己沉入題海,幫助學生浮出題海的人.一節課45分鐘的時間,應該是教師與學生共同碰撞與促進的過程,好的例題與變式,能夠發展學生思維,促進提升數學素養.

