高考命題有依據 復習備考有目標

?江蘇省南京市大廠高級中學

李素娟

1 引言

“立德樹人”是歷年高考數學命題的指導思想，在這一核心功能指導下，全面貫徹高考評價體系的要求，推動人才培養的改革創新，引領并指導高中數學教育與教學，得以合理選拔高一層次人才.因而，高考數學命題有據可依，試卷必須充分體現數學學科的特點，突出數學必備知識的考查，合理引導教學，倡導育人為本、遵循教育規律、回歸數學教材等的落實，為復習備考提供明確的目標.

2 核心素養引領復習方向

培養數學學科核心素養是為了更好地促進學生形成“三觀正”(正確的人生觀、價值觀、世界觀)、“用數學”的目的.借助數學的眼光觀察世界，發展一般性素養——主要涉及數學抽象、直觀想象；借助數學的思維分析世界，發展嚴謹性素養——主要涉及邏輯推理、數學運算；借助數學的語言表達世界，發展應用性素養——主要涉及數學建模、數據分析.從培養數學學科核心素養角度入手來設置命題，為復習備考指明方向.

A.圓 B.橢圓 C.拋物線 D.直線

分析：根據題目條件，取平面內的兩個定點A，B的極端位置——A，B重合，達到兩點合二為一來分析與處理問題，并把特殊情況下得到的結論反饋到題目中去，選擇與之相符合的結論，從而得以巧妙邏輯推理，合理破解.破解本題的方法很多，不同方法涉及不同的核心素養與數學知識.

復習備考建議：正確把握高中數學課程標準與教學大綱、高中數學教學、高考數學命題以及數學核心素養等之間的關系，有針對性地安排實例與練習，就六個方面的核心素養借助數學的眼光、數學的思維、數學的語言等視角切入，合理強化訓練，落實核心素養的培養.

3 夯實教材為高考筑基

數學教材是歷年高考命題之源，典例之根，母題之庫.而高考試題主要考查主干知識、能力和素養，側重于思維、應用、創新，從“解題”上升到“解決問題”，從“做題”升華到“做人做事”，直到提升綜合素養.在數學學科素養導向新舉措、能力考查新突破的形勢下，相當數量的高考試題都能在數學教材中尋覓其“影蹤”，找到相關的背景、面孔、變形、拓展與提升等，從回歸數學教材角度入手來設置命題，為復習備考提供藍本.

分析：根據題目條件，先確定焦點的坐標，進而確定焦點弦所對應的直線方程，聯立直線與拋物線方程，消元后轉化為相應的二次方程，結合二次方程的實數根，利用弦長公式加以運算即可確定.

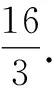
鏈接教材：

普通高中課程標準實驗教科書《數學·選修2-1(A版)》(人民教育出版社，2007年2月第2版)第69頁例4：

斜率為1的直線l經過拋物線y2=4x的焦點F，且與拋物線交于A，B兩點，求線段AB的長.

復習備考建議：高考命題經常是源于教材意料之外，植于教材情理之中，高于教材能力之上.在復習備考時，充分理解與掌握數學的知識體系、框架結構、公式定理、例題習題等，進一步對教材內容進行組合、加工和拓展，挖掘知識本源，“重視很多習題潛在著進一步擴展其教學功能、發展功能和教育功能的可行性”.

4 高考真題延續往年精髓

往屆高考真題已然成為新一屆高考命題的一個極佳的“試題庫”“題源庫”，通過變形、轉化、深入、創新、拓展應用等手段加以合理改編，承載指導數學教學與學習中的示范與引領作用.而深入研究往屆的一些典型高考試題，對把握高考命題規律，感悟高考熱點、重點及其考查方式，探尋培養數學學科素養的途徑，提高應考能力和復習效率等都大有益處.從高考真題角度入手設置命題，為復習備考提前演練.

例3(2020年高考數學全國卷Ⅰ理科第14題)設a，b為單位向量，且|a+b|=1，則|a-b|=______.

分析：對條件中平面向量和的模加以平方處理，通過數量積公式的轉化與應用，確定對應數量積的值，再通過平面向量差的模的平方處理來轉化與運算，進而得以求解.

其實該高考命題來源于2004年高考數學全國卷Ⅱ文科第9題.通過兩向量a，b的模以及對應平面向量的和(或差)的模來求解相應平面向量的差(或和)的模問題.破解時，可以利用平面向量的數量積公式或坐標法來處理，也可以借助“平行四邊形四邊的平方和等于兩條對角線的平方和”的公式來處理.

高考真題(2004年高考數學全國卷Ⅱ文科第9題)已知向量a，b滿足|a|=1，|b|=2，|a-b|=2，則|a+b|=( ).

(答案：D)

復習備考建議：高考復習備考一定要“知己知彼”，才能“百戰百勝”.特別是有針對性做一些歷年高考中的同一知識點的相關典型實例，從數學知識、數學思想方法與數學能力等角度切入，不斷理解并掌握對應的實質，領悟并升華思想方法，挖掘并拓展數學能力，為我所用，融會貫通，真正分享歷年高考真題的智慧，不斷提升數學能力與核心素養.

5 科學育人巧融高考命題

高考命題倡導“五育”(德智體美勞)并舉的根本目標，有效落實“五育”，全面提升人文素養.高考數學試題也經常融入政治經濟、科學文化、藝術哲學、道德修養、價值理念等“五育”元素，交匯數學，特別是合理設置創新情境，結合社會現實，貼近生活實際，關注時代熱點，充分體現數學實際應用價值以及育人價值.從科學育人角度入手設置命題，為復習備考創設情境.

例4(2020年高考數學全國卷Ⅱ理科第3題，文科第4題)在新冠肺炎疫情防控期間，某超市開通網上銷售業務，每天能完成1 200份訂單的配貨，由于訂單量大幅增加，導致訂單積壓.為解決困難，許多志愿者踴躍報名參加配貨工作.已知該超市某日積壓500份訂單未配貨，預計第二天的新訂單超過1 600份的概率為0.05，志愿者每人每天能完成50份訂單的配貨，為使第二天完成積壓訂單及當日訂單的配貨的概率不小于0.95，則至少需要志愿者( ).

A.10名 B.18名 C.24名 D.32名

分析：結合閱讀與理解，通過概率與對應的數據分析，歸納與總結出題目的內涵，合理構建數學模型，合理調配志愿者.

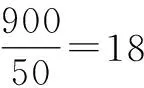
故選：B.

復習備考建議：在復習備考過程中，有針對性結合一些相關“五育”(德智體美勞)實例的問題，通過問題背景的巧妙設置，合理把高考數學與育人根本目標進行有機融合，充分體現高考數學的指導性功能與方向性意義.復習備考關鍵在于引導學生對問題的理解、分析、剖析、建模等，并結合數學相關知識來進一步融合與深入，拓展數學創新與應用，體現數學特色.

6 結束語

合理借助核心素養引領復習方向，落實命題指導思想；夯實教材只為高考筑基，復習應回歸數學教材；高考真題延續往年精髓，要合理應用歷年真題；科學育人巧融高考命題，可創新情境巧妙設置.把握改革精神，創新試題設計，優化試卷結構，明確復習方向，全面對學生的數學語言的閱讀、理解、轉化、表達等能力加以不斷深化，緊緊抓住數學基礎知識和基本技能，從基礎入手，不斷深入，有效復習，全面提升.