基于電磁模態分析的埋地電纜高頻電氣參數計算研究

馬馳， 李江濤， 張伯昱， 嚴澤鑫， 孫子涵

(西安交通大學 電力設備電氣絕緣國家重點實驗室，陜西 西安 710049)

0 引 言

在對電力系統電磁暫態過程(electromagnetic transient process,EMTP)進行分析時，往往會涉及埋地電纜高頻下的串聯阻抗矩陣、并聯導納矩陣計算。現有大部分的電磁暫態分析程序，如電磁暫態程序(electromagnetic transient programs - the alternative transients program, EMTP-ATP)、電力系統計算機輔助設計軟件(power systems computer aided design, PSCAD)等，其對電纜阻抗、導納參數的計算通常使用準靜態電磁場條件[1]。在低頻條件下，土壤中的位移電流遠小于傳導電流，準靜態電磁場條件不會引起較大誤差；但隨著頻率升高到0.1MHz左右，土壤中位移電流大小的數量級與傳導電流可比，此時傳統的解析算法精度開始下降。此外，傳統的解析算法在計算電纜阻抗、導納參數時往往只考慮集膚效應，卻無法將鄰近效應帶來的影響考慮在內[2]。

針對埋地電纜的參數計算，許多學者對此進行了研究。Wedephol等提出了同軸電纜阻抗、導納矩陣參數的解析算法[3]，Ametani在此基礎上將電纜參數的計算擴展到含纜芯、屏蔽、鎧裝三導體模型，并將算法應用于EMTP-ATP的CABLE CONSTANTS子程序中[4]。但是，上述方法都是建立在準靜態電磁場中，忽略了位移電流及鄰近效應，使得高頻下參數的準確性受到影響；Ametani等采用對導體分區的方法計算含鄰近效應的電纜參數矩陣[5-6]，然而導體分區的過程十分繁瑣，且會帶來大量的時間成本，在實際工程中難以應用。文獻[7]利用表面導納算子對埋地電纜的串聯阻抗矩陣進行計算，但是其計算過程工作量大、模型適應性差，難以適用于實際工程計算中。

在對埋地電纜的串聯阻抗及并聯導納矩陣進行計算時，尤其是在高頻條件下，大地返回阻抗的計算至關重要。Pollaczek[8]第一個推導出埋地導線大地返回自、互阻抗的精確公式。Pollaczek公式中的無窮積分項不易計算，Wedephol[3]用截斷無窮級數的方法對Pollaczek公式進行計算。Srivallipuranandan[9]以Romberg外推法為基礎對Pollaczek公式中的無窮積分項直接進行數值積分，但因被積函數的劇烈震蕩特性使得直接數值積分并不容易。Ametani[4]使用Carson公式近似計算大地返回阻抗。上述計算大地返回阻抗的解析公式的問題在于，隨著頻率的增加，積分項需要更長的時間才能收斂，導致截斷誤差；當頻率接近1 MHz時，積分中的某些項會出現劇烈震蕩的現象。Petrache[10]提出了一種簡單的接地阻抗對數近似法，該法未考慮電纜的埋深，這可能會導致結果的誤差。

本文采用有限元方法求解波動方程，對埋在有損土壤中任意截面的多導體電纜進行電磁模態分析。目前，已經有許多學者利用有限元法對電纜的參數進行計算[11-14]，但是這些方法都是建立在準靜態電場條件下，其對位移電流的忽略可能造成高頻下計算結果的誤差。本文將電纜二維截面上電磁場的分布以及各種模式下傳播常數的求解問題轉化為對波動方程特征值的求解。在求得二維截面上電磁場的分布后，對電場及磁場進行積分，即可得到電纜中導體的電壓、電流大小，從而通過進一步計算得到埋地電纜的串聯阻抗及并聯導納矩陣。

1 電磁模態分析理論

對埋地電纜進行電磁模態分析，由于相域中電纜各導體存在電磁耦合，無法直接計算單一的傳播常數，因此需要利用相模變換將電纜導體的電壓、電流關系從相域轉化為模域[15]，從而實現解耦。解耦后的電纜會存在不同的工作模式，對不同工作模式下電纜參數的計算需要至于時變電磁場中，以考慮高頻下土壤中位移電流帶來的影響。

1.1 相模變換理論

對含有n個導體的電纜系統，其存在n個獨立的模式[16]。

首先研究單根電纜，以圖1所示的雙導體同軸電纜(導體為纜芯、護層)為例，假設電纜內的正弦電磁波沿z軸方向傳播，其時域電波方程如下：

(1)

(2)

圖1 雙導體同軸電纜截面圖Fig.1 Cross section of a two-conductor coaxial cable

方程中U=[U1U2]T表示電纜中導體的電壓向量，I=[I1I2]T表示電纜中導體的電流向量，Z表示兩導體的串聯阻抗矩陣，Y表示兩導體的并聯導納矩陣。由式(1)、式(2)可以推導出電纜內電磁波沿z軸方向傳播的二維波動方程：

(3)

因為矩陣Z和矩陣Y都是對稱陣，故式(3)中的矩陣YZ為矩陣ZY的轉置，二者具有相同的特征值。現假設存在可逆矩陣S、Q，將相域中的電壓電流向量U、I轉換為模域中的電壓電流向量Um、Im，即

(4)

若以下關系成立，則矩陣S、Q分別實現了對矩陣ZY、YZ的相似對角化：

(5)

式中：λ為矩陣ZY、YZ的特征值構成的相似對角陣，S、Q為特征值對應特征向量構成的矩陣。

由以上分析可知，通過對矩陣ZY、YZ的相似對角化處理，即可相域中的電壓、電流向量U、I轉換為模域中的電壓電流向量Um、Im，兩個導體組成的電纜系統即對應于模域中的兩個模式。因為矩陣ZY變換為了對角陣，模域中的各模態電壓、電流向量間不存在相互耦合關系，第k(k=1,2)個模式的傳播常數γk即對應于矩陣λ中第k個特征值λk的平方根值

(6)

式中：αk對應于第k個模式的衰減常數；而βk對應于第k個模式的相位常數。

隨著頻率逐漸升高，在高頻下，變換矩陣S中元素的虛部變得很小，通常可以忽略不計。通過分析相域電流I和模域電流Im之間的關系，可以得到第k個模式下對應的相域電流的分布。以雙導體電纜為例，其變換矩陣Q為2階方陣，將矩陣Q進行列分塊，則式(4)中的第二個公式可以變形為

(7)

令Im1=1，Im2=0，可以得到第1個模式下電纜中導體的相域電流分布；同理令Im1=0，Im2=1，可以得到第2個模式下電纜中導體的相域電流分布。通過上述分析可知，變換矩陣Q的每一列都對應于相應模式下的相域電流分布。

對于雙導體同軸電纜而言，其在高頻下一般存在兩種工作模式：接地模式和同軸模式。接地模式表示電流不經過纜芯，直接由護層和大地構成回路;同軸模式表示電流從纜芯流入，從護層返回，從而構成通路。兩種模式對應的相域電流分布如圖2所示。

圖2 雙導體同軸電纜不同模式下相域電流分布Fig.2 Phase domain current distribution of a two-conductor coaxial cable under different modes

相模變換理論可以推廣至多根埋地電纜的模型中。假設現有三根雙導體同軸電纜呈水平排布，則整個電纜系統中的導體總數為6，在高頻下存在6個不同的模式：3種同軸模式、兩種內護層模式和一種接地模式。記三根導體分別為A、B、C，則這6種模式對應的相域電流分布如圖3所示。

圖3 3根雙導體同軸電纜不同模式下相域電流分布Fig.3 Phase domain current distribution of three two-conductor coaxial cables under different modes

1.2 不同模式電磁場的計算

在時變電磁場中，通常使用麥克斯韋方程組對電磁波的傳播特性進行研究。假設所要分析的空間中無自由電荷，則麥克斯韋方程組可以表示如下：

(8)

麥克斯韋方程組中的第一個方程為全定律電流，全電流可以變形為

(9)

故只要導體滿足似穩條件ωε/σ<<1，即可忽略位移電流。一般金屬導體的電導率σ≥107S·m，故在電磁暫態計算關注的頻率范圍內，金屬內的位移電流均可忽略。對于土壤，其電導率很低，在高頻下土壤中位移電流的大小往往不可忽略。對于某些導電性很差的土壤，從50 kHz開始位移電流的大小就不能忽略，屬于電磁暫態模擬關注的范圍。

因此，在利用電磁模態分析對電纜參數進行計算時，可以對電纜中纜芯、護套等導體層中的位移電流進行忽略，僅僅計及土壤中的位移電流分布即可。

在三維坐標空間中，假設電纜中的電磁波沿著z軸方向傳播，由全電流定律和電磁感應定律，可以得到如下方程：

(10)

(11)

γ=αz+jβ。

(12)

式中：kz表示面外波數；k0表示真空中的波數；α表示電磁波沿z軸方向傳播時的衰減常數；β表示電磁波沿z軸方向傳播時的相位常數。利用有限元法，即可將二維截面上電場、磁場的求解轉化為對方程特征值問題的求解。圖4給出了雙導體同軸電纜在接地模式和同軸模式下的電場強度分布云圖。

圖4 雙導體同軸電纜不同模式電場強度云圖Fig.4 Cloud diagram of electric field intensity of two-conductor coaxial cable under different modes

在利用有限元法對電纜中的電磁場進行模擬時，需要設置一個范圍很大的截斷空間，在截斷空間的邊界上設置表面電流密度為0。截斷空間半徑的確定方法如下：

對于滲透進土壤的交流電流，其在土壤中的散流程度可以用大地滲透深度進行表示，即為

(13)

式中：μ0表示真空中的磁導率；σ表示土壤的電導率；ρearth表示土壤的電阻率。

在設置截斷空間來模擬空氣及大地時，至少應將截斷半徑設置為3～5倍的大地滲透深度。對電阻率為50 Ω·m的土壤來說，其在工頻下的透入深度約為0.5 km，意味著在使用有限元法建立工頻下的土壤模型時，其截斷半徑至少為1.5 km，形成的巨大網格將極大的增加計算時間。因此，雖然使用電磁模態分析可以計算低頻下的電纜參數，但卻會帶來巨大的時間成本，且低頻下已有解析公式的計算精度已經足夠。

2 高頻下電纜電氣參數的計算

在高頻下，利用有限元法對地下電纜進行電磁模態分析，可以得到各種模式下電纜的傳播常數、電磁場分布。根據求得的傳播常數，可以計算各模式下電磁波的衰減常數和波速；根據各模式下電磁場的分布，經過一系列變換，可以計算埋地電纜的串聯阻抗矩陣及并聯導納矩陣。

2.1 各模式衰減常數、波速及相對波速的計算

建立埋地電纜模型后，可以根據有效折射率對想要求得的模式進行搜索，并在此過程中求得各模式下電磁波的傳播常數。由式(12)可知，求解器求得的復傳播常數的實部αz，即是電磁波在該模式下的衰減常數，表征電磁波在傳播方向上每單位長度的振幅和能量衰減程度。根據電磁波理論，波速可以由下述公式求得：

(14)

式中：ω表示角頻率；β表示相位常數(對應于傳播常數的虛部)。

在電磁暫態分析和有關電纜的故障診斷、定位中，經常實際波速相對于真空波速的比值，即相對波速，可以表示為

(15)

式中：c表示真空中的光速；β表示真空中波的相位常數(也可理解為真空波數k0)，可以用關系式β=k0=ω/c進行求解。

2.2 電纜串聯阻抗、并聯導納矩陣的計算

假設電纜中電磁波沿z軸方向傳播，電纜中導體的電壓向量U和電流向量I可以作如下改寫：

(16)

(17)

將式(16)、式(17)代入時域電報方程(1)、方程(2)，可以得到以下關系：

(18)

(19)

對于不同的模式，電磁波具有不同的傳播常數γ，可以列寫不同模式下的式(18)、式(19)。對于雙導體同軸電纜，兩個模式下的傳播常數已經求出，只要知道對應模式下導體的電壓、電流值，即可以通過下述關系求出電纜的串聯阻抗和并聯導納矩陣：

(20)

(21)

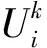
上文通過有限元法求解了不同模式下電纜內的電場分布和磁場分布。電纜的埋設圖如圖5所示。圖中O點為電壓參考點，不同參考點的選取可能對結果產生輕微影響。在高頻條件下，導體的表面可以看做等位面，因此沿線l1和l2作電場強度的線積分，即可得到兩個導體的電壓值；沿面S1、S2作電流密度的面積分，即可得到兩個導體的電流值：

(22)

(23)

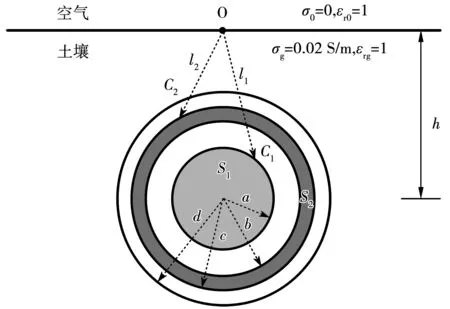
圖5 地下雙導體同軸電纜截面圖Fig.5 Cross section of an underground two-conductor coaxial cable

3 案例分析

以單根雙導體同軸電纜為例進行分析：首先，在電磁暫態仿真軟件EMTP-ATP中計算其利用傳統解析法得出的串聯阻抗和并聯導納矩陣；其次，利用電磁模態法計算頻率f≥0.5 MHz時的串聯阻抗和并聯導納矩陣，并將上述兩者的計算結果進行對比；最后，在EMTP-ATP中建立JMarti模型進行時域仿真，并利用電磁模態法的計算結果替換f≥0.5 MHz時的輸入參數文件，將傳統解析法和電磁模態法得到的時域波形進行對比。

3.1 單根雙導體同軸電纜

假設有一雙導體同軸電纜，其結構如圖5所示。電纜的幾何半徑設為：a=2 cm，b=3.75 cm，c=4 cm，d=5 cm；纜芯的電導率σc=9×107S/m，護層的電導率σS=4×107S/m；模型中導體、絕緣、空氣以及土壤的相對磁導率全部設置為1；內絕緣的相對介電常數εr1=3，外絕緣的相對介電常數εr2=3，導體、空氣及土壤的相對介電常數全部設置為1。如圖5所示，空氣的電導率σ0=0，土壤的電導率σg=0.02 S/m。電纜的埋深h分別設置為0.1、0.25和1 m，以便對比不同埋深下電纜的高頻參數特性。

圖6、圖7分別給出了不同埋深下，衰減常數以及相對波速隨頻率變化的關系圖。圖中，模式1表示單根雙導體同軸電纜的接地模式，模式2表示單根雙導體同軸電纜的同軸模式。

圖6 單根埋地電纜衰減常數隨頻率變化關系圖Fig.6 Variation of the attenuation constant with frequency of a two-conductor coaxial cable

由圖6、圖7可以發現，對于單根雙導體同軸電纜而言，相較于同軸模式，接地模式擁有更高的衰減程度，其相對波速卻更低。Ametani[15]分析了不同模式下電磁波傳播路徑的阻抗和電容的影響，對其進行了解釋：對接地模式而言，電流從護層進入，流經大地后返回護層，回路中包含數值較大的大地返回阻抗，且外絕緣與大地間的電容較大，使得電磁波傳播過程中有較多電流泄入大地，導致電磁波以很快的速度衰減且波速較慢；對同軸模式而言，其與大地間的電磁聯系不強，故其具有更低的衰減常數和更高的波速。

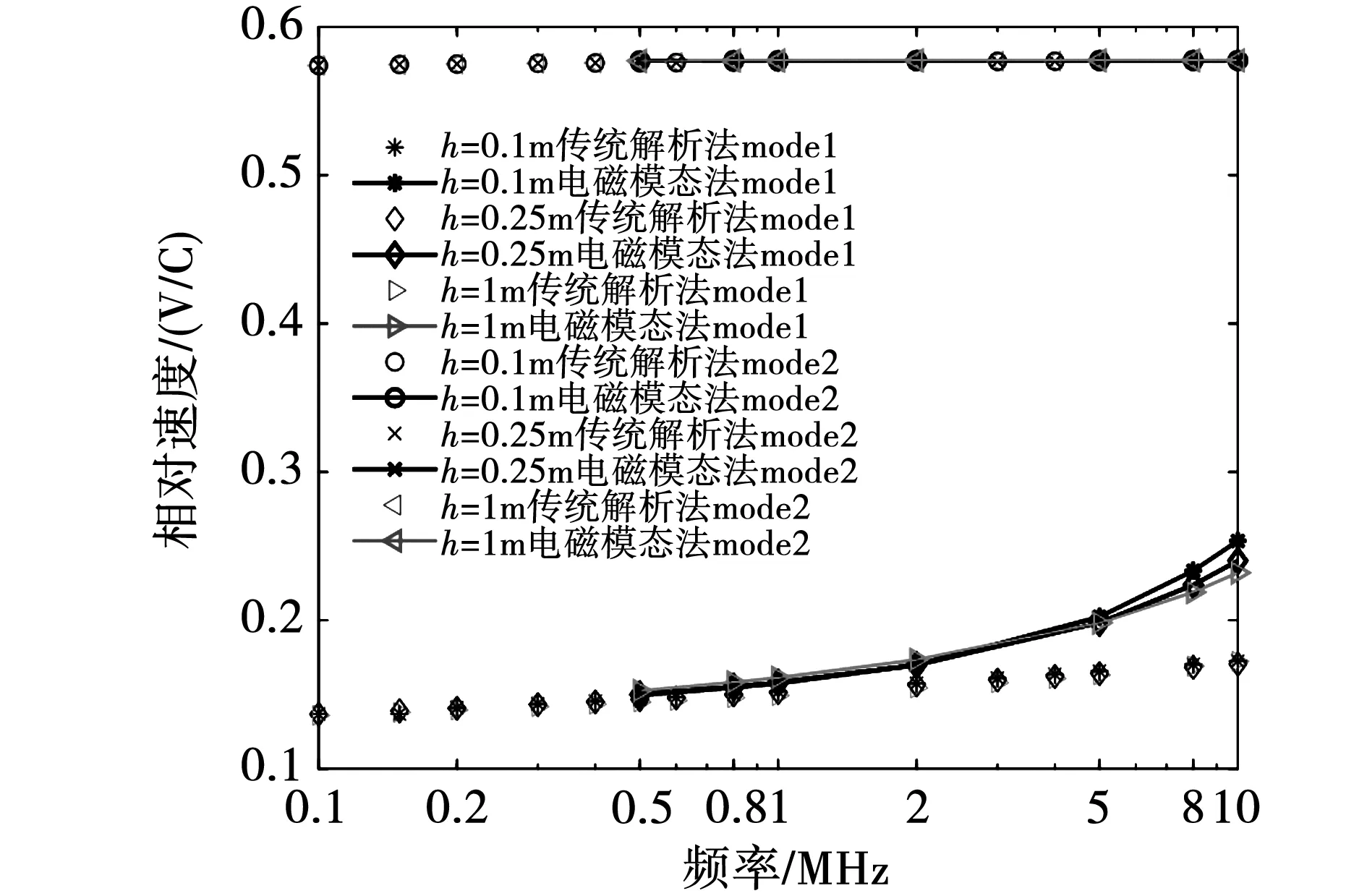
圖7 單根埋地電纜相對波速隨頻率變化關系圖Fig.7 Variation of the relative velocity with frequency of a two-conductor coaxial cable

圖8給出了不同埋深下，電纜的串聯阻抗中的元素隨頻率變化的關系圖。由于纜芯與護層的互阻抗、護層的自阻抗與纜芯的自阻抗值十分相似，故圖8中只給出了元素R11、L11隨頻率變化的關系圖。

圖8 單根埋地電纜串聯阻抗矩陣隨頻率變化關系圖Fig.8 Variation of the series impedance matrix with frequency of a two-conductor coaxial cable

由圖8可以看出，當頻率升至0.5 MHz時，傳統解析法與電磁模態法的計算結果開始呈現明顯差異。相較于傳統的解析算法，利用電磁模態法計算得到的串聯阻抗矩陣元素的電阻更大，電感更小；電纜的埋深越大，自電阻及互電阻越大，自電感和互電感越小。

圖9給出了不同埋深下，電纜的并聯導納中的元素隨頻率變化的關系圖。本文建立的電纜中不考慮半導體層的影響，故并聯導納矩陣中的并聯電導部分可以忽略；對于考慮半導體層影響的電纜，則需考慮并聯電導的影響。

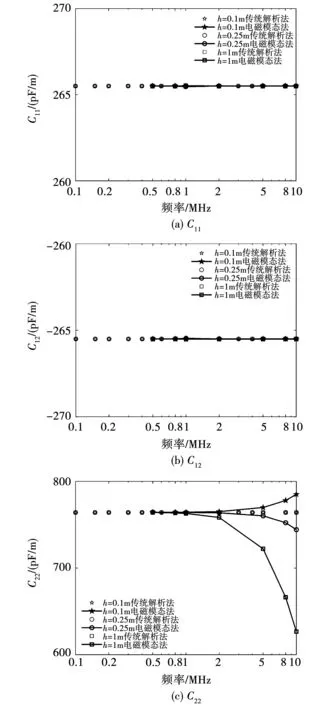
圖9 單根埋地電纜并聯導納矩陣隨頻率變化關系圖Fig.9 Variation of the shunt admittance with frequency of a two-conductor coaxial cable

由圖9可以看出，對于纜芯和護層間的電容，兩種方法的計算結果完全相同；對于護層的自電容，由于其包含護層對地的電容，由于電磁模態法考慮了高頻下的位移電流的影響，故當頻率升至0.5 MHz時兩種計算方法的結果開始呈現明顯差異。

3.2 時域仿真

為了進一步說明電磁模態法與傳統解析法對電磁暫態計算造成的影響，故需在時域中探究兩種方法計算得到暫態波形的差異。相較于同軸模式，接地模式的電磁暫態過程與大地間的聯系更為緊密，故選取接地模式作為時域暫態仿真的電路，如圖10所示。

圖10 接地模式的電路模型Fig.10 Circuit model of grounding mode

圖中，電纜的截面形狀如圖5所示，電纜的電氣參數設置與3.1中的雙導體同軸電纜的設置相同。電纜長度為1 km，埋深為0.25 m。

首先在EMTP-ATP中采用頻率相關的JMarti模型，對線路分別施加1.2/50微秒的雷電波、1.2/5微秒的雷電波以0.1/1微秒的VFTO，得到輸出波形；接著用電磁模態法計算得到的串聯阻抗和并聯導納矩陣替換原EMTP-ATP輸入文件中頻率大于等于500 kHz的部分，得到輸出波形，并將結果與EMTP-ATP中直接使用解析法得到的結果進行對比。圖11給出了不同激勵下使用傳統解析法和電磁模態法輸出的暫態過電壓波形。

由圖11可知，在接地模式下，當主頻率較高、波前較陡的過電壓波侵入電纜時，相較于傳統的解析算法，將電磁模態法得到的串聯阻抗和并聯導納矩陣應用于暫態計算時，其波形的傳播速度更快，二者在極短的暫態時間內存在一些差異。當土壤電阻率越高、大地的相對介電常數越大時，大地中位移電流的影響越大，兩種方法得到的暫態波形的差異越明顯。

4 結 論

在高頻條件下(f≥0.5 MHz)，大地中的位移電流會對埋地電纜串聯阻抗及并聯導納矩陣的計算產生較大影響，原有準靜態電磁場下的解析算法對位移電流的忽略可能會使結果產生較大偏差，具體的偏差與電纜的結構、埋深、土壤電阻率等因素有關；在時域下的仿真說明了高頻下串聯阻抗及并聯導納矩陣的差異可能會導致電磁暫態計算結果的差異。位移電流的影響直接決定了時域中輸出波形的差異大小，若大地電阻率越高、介電常數越大，則位移電流的影響越大，傳統解析法和電磁模態法的時域仿真結果的差異越大。