軸壓比對不同類型ECC框架節點抗震性能影響
李曉琴,丁 捷,張 田,2,張田慶
(1.昆明理工大學建筑工程學院土木工程系,云南昆明 650500;2.北京邁達斯技術有限公司,云南昆明 650501;3.中國建筑第二工程局有限公司,云南昆明 650500)
引 言
鋼筋混凝土框架結構是最常見的一種建筑結構形式。在地震作用下,鋼筋混凝土框架結構主要有填充墻破壞、樓梯破壞和梁柱節點破壞[1]等破壞形式。多數情況下,鋼筋混凝土框架的倒塌,是由節點破壞引起的[2]。例如,2008年汶川地震震后調查[3]表明,大部分框架結構的倒塌是因節點在地震作用下發生嚴重脆性破壞導致;1995年日本Kobe 地震,大量鋼筋混凝土建筑中框架節點核心處發生脆性剪切破壞,導致結構倒塌[4]。框架節點是結構在地震作用下保持抗倒塌能力的重要構件,保證框架節點在地震作用下的延性破壞是確保結構抗震性能的重要因素。
傳統鋼筋混凝土框架節點由于普通混凝土韌性差、易出現裂縫等缺點,導致框架節點易產生脆性破壞。Khaled 等[5]使用外貼FRP 復合材料增強十字型框架節點,結果表明該加固方法可以提高框架節點在地震作用下的抗剪能力及延性,但承載力下降較快。Prota 等[6]使用外貼碳纖維布和碳纖維筋替換鋼筋的加固方法加固RC 框架節點,結果表明該加固方法可以顯著提高節點柱抗震承載力,但節點仍表現出脆性破壞的特征。可見,僅靠外貼碳纖維布提高節點抗震強度加固效率不高,可考慮采用強度較高、韌性較好的材料替代混凝土進行框架節點設計或加固。
鞠彥忠等[7]采用活性粉末混凝土(Reactive Powder Concrete,簡稱RPC)作為節點的填充材料,進行了不同軸壓比下配箍率對節點抗震性能影響的數值分析。結果表明,增加節點核心區的配箍率,可以提升構件在高軸壓比下的塑性變形能力以及延性,防止RPC 因強度過高而導致構件發生脆性破壞。素RPC 材料的極限拉伸應變一般可達1%,根據試驗結果可知,在框架節點區域采用強度過高的材料替換普通混凝土,對增加節點的抗震性能,特別是延性作用不大。高韌性纖維增強水泥基復合材料(Engineering Cementitious Composites,簡稱ECC)[8]強度等級可保持與普通混凝土相同或略強,而其極限拉伸應變是普通混凝土的300~500 倍[9],具有多縫開裂以及應變硬化的特征,表現出高韌性、高耗能等特征,解決了普通混凝土自身脆性的缺點[8?9]。并且ECC 中纖維起到橋接作用,構件破壞模式由單一裂縫轉變到多條小裂縫穩態發展,與鋼筋間不易產生滑移。ECC 替代普通混凝土可以提高地震作用下節點的損傷容限和能量吸收能力。
盡管已有研究提出軸壓比對混凝土框架節點抗震性能的重要性,也已有規范[10?11]規定混凝土框架節點軸壓比的限值,但目前為止,尚未有研究系統地提出軸壓比對不同ECC 框架節點類型抗震性能的影響以及軸壓比的限值。采用試驗方法費工費時,為了給后續試驗研究做出充分、精準的預判,本文采用數值模擬方法對框架節點進行分析。以Yuan等[12]和梁興文等[13]的ECC 框架節點試驗數據為基礎,采用有限元軟件ABAQUS 中的混凝土塑性損傷(Concrete Damaged Plasticity,CDP)[14]模型模擬混凝土。同時采用QU[15]改進Clough 提出的考慮鋼筋?混凝土界面黏結滑移作用的滯回鋼筋模型模擬鋼筋,對比試驗結果與計算結果,驗證有限元模型的可靠性。建立不同軸壓比下十字型及T 型ECC 框架節點計算模型。ECC 框架節點的抗震性能通過位移延性系數μ、等效黏滯阻尼系數ξ和割線剛度Ki來評價。最后根據軸壓比與評價指標,給出不同類型ECC 框架節點設計軸壓比的下限值。
1 低周循環荷載下框架節點位移延性系數μ 影響因素分析
通常來說,框架節點在地震作用下會出現不同的破壞形態,如梁、柱端彎曲破壞、節點核心區彎曲破壞、節點區剪切破壞和剪切黏結破壞等。其中,節點核心區彎曲破壞分為大偏心受壓破壞和小偏心受壓破壞。延性系數是評價結構延性的首要指標,也是區分框架結構延性破壞與脆性破壞的重要指標。延性系數一般分為曲率延性系數μφ[16]和位移延性系數μ[17]。由于曲率延性系數μφ只單方面評價截面的延性性能,并不能體現出框架節點整體的延性,所以本文采用反映構件整體宏觀延性性能的位移延性系數μ來評價框架的延性性能。
分析已有試驗[18?20]中軸壓比、剪壓比、剪跨比及配箍率4 個因素對框架節點位移延性系數μ的影響,可明確影響框架節點延性破壞的主控因素,如圖1所示。從圖1可知,當軸壓比、剪壓比、配筋率和剪跨比每變化30%時,對應的位移延性系數μ分別變化40.85%,1.02%,2.09% 和13.40%。因此,當軸壓比、剪壓比、剪跨比及配箍率等因素在規范[10]的可控范圍之內,軸壓比對位移延性系數μ的影響較明顯,可作為評價框架節點是否發生延性破壞的主控因素之一。

圖1 軸壓比、剪壓比、配箍率及剪跨比對位移延性系數的影響Fig.1 Influence of axial compression ratio,shear compres?sion ratio,stirrup ratio and shear span ratio on dis?placement ductility coefficient
已有研究[12,21?23]基于不同軸壓比(0.12,0.15,0.4及0.68~0.712)對RC 及R?ECC 框架節點進行了抗震性能分析,如表1所示。通過對比節點的位移延性系數和耗能能力,可以看出R?ECC 節點要比RC節點延性及耗能能力更好。其中,梁興文等[13]采用的節點類型為ECC 填充核心區十字型節點,體積配箍率為0.152~0.380;Yuan 等[22]采用的節點類型為ECC 填充核心區T 型節點,體積配箍率為0~0.690;通常來說,不同類型及配筋的框架節點發生延性破壞的位移延性系數μ不同,所以僅基于以上試驗數據無法得出ECC 框架節點的軸壓比限值。因此,本文按照常見的T 型及十字型框架節點,基于相同的加載制度及尺寸配筋條件下擬采用0.3,0.5,0.7 及0.9 設計軸壓比,按照不同節點類型研究ECC 框架節點的軸壓比限值。

表1 R-ECC 與RC 框架節點在不同軸壓比下的表現Tab.1 Performance of R-ECC and RC frame joints under different axial compression ratios
2 循環荷載下ECC 框架節點數值模型
2.1 試驗原型
唐九如[24]按節點位置不同,將框架節點分為4種類型。中層中節點(十字型)、頂層中節點(T 型)、中部邊節點(T 型)和角節點。其中中層中節點的柱和梁都處于框架中間,易發生變形和節點區剪切破壞。中部邊節點雖達到了“強柱弱梁”的設計原則,但由于梁端易出現黏結滑移等現象,會出現剪切黏結破壞,也是損傷較為嚴重的節點類型。而頂層中節點柱端易產生塑性鉸,一般發生柱端彎曲破壞。角節點由于在框架結構中數量較少,一般情況下發生核心區彎曲破壞。因此本文主要針對中層中節點和中部邊節點2 種易損節點類型建立計算模型,進行抗震性能分析。為確保計算模型的可靠性,本文采用Yuan 等[12]及梁興文等[13]的試驗原型進行計算模型驗證。具體試件配筋尺寸如圖2,3 所示,試驗結果如表2所示。

圖2 S5 試件尺寸及配筋(單位:mm)Fig.2 Specimen size and reinforcements of S5(Unit:mm)
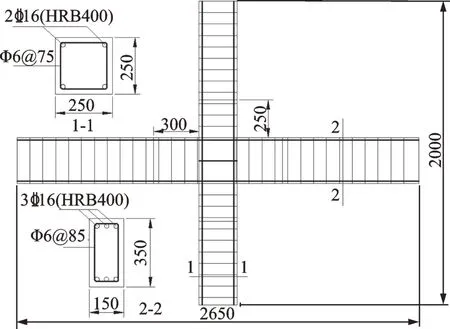
圖3 試件FRCJ4 尺寸及配筋(單位:mm)Fig.3 Specimen size and reinforcement of FRCJ4(Unit:mm)

表2 試驗信息Tab.2 Test details
2.2 ECC 框架節點計算模型
2.2.1 ECC 材料模型
ECC 是一種高韌性、高拉伸應變的新型水泥基復合材料,極限拉伸應變是普通混凝土的300 倍以上。Meng 等[25]經過大量ECC 拉伸試驗,將ECC 的受拉階段分為彈性階段、多縫開裂階段和應變硬化階段。Feenstra 等[26]將ECC 的受壓過程用斷裂能表示,并用拋物線的形式表示受拉受壓曲線。ECC 材料的拉壓斷裂能均應為不變量,但由于在受拉模式下ECC 呈現出應變硬化,在達到峰值應力后迅速失去承載能力,軟化不明顯,因此ECC 受拉模式采用應力應變關系定義;而受壓模式下ECC 在達到峰值應力后軟化明顯,在不同單元特征長度下應采用不同的應力應變關系曲線以保證受壓模式斷裂能Gc為常數。
ECC 的受拉應力?應變曲線和受壓應力?應變曲線如圖4(a),(b)所示。

圖4 ECC 應力-應變曲線[25?26]Fig.4 ECC stress-strain curve[25?26]
ECC 受拉本構計算方程為[25]:
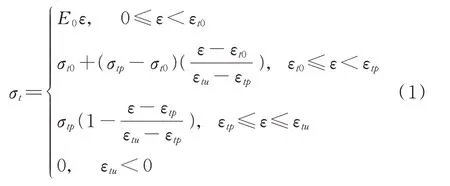
式中E0為材料初始彈性模型;σt為ECC 的受拉應力;σt0為初裂拉應力;ε為ECC 在受拉應力狀態下的應變;εt0為初裂拉應力相對的應變;σtp為極限拉應力;εtp為極限拉應力相對的拉應變;εtu為極限拉應變。
ECC 受壓本構計算方程為[26]:
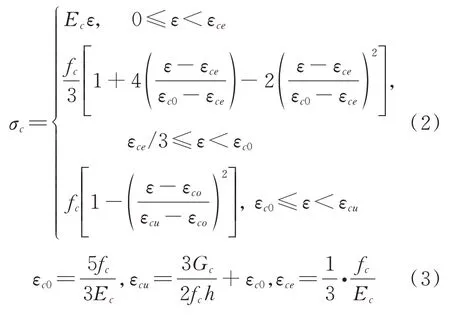
式中σc為ECC 的受壓應力;Ec為ECC 的彈性模量;ε為ECC 在受壓應力狀態下的應變;fc為ECC 的峰值抗壓強度;εc0為fc對應的應變;εce為對應的應變,εcu為極限壓應變;h為有限元模型單元特征長度,,A為單元體積;Gc為受壓斷裂能。
本文根據Amrane 等[27]提出的能量等價原理[28]提出了適用于有限元軟件ABAQUS 中CDP 模型的ECC 損傷因子的計算方法。根據損傷理論,將ECC的本構關系和能量等價原理[27]結合推導ECC 損傷因子,得出損傷因子dc,dt的計算方法,并將該計算方法引入到有限元軟件ABAQUS 的CDP 模型中,如下式所示:

式中σk為混凝土抗壓或拉伸應力,單位為MPa;ε為總應變;d為損傷因子。
將帶有損傷的應力?應變關系代入上述ECC 本構模型中,可得出受拉損傷因子dt和受壓損傷因子dc的方程:

在單軸循環荷載下,Lee 等[14]提出使用拉伸等效塑性應變和壓縮等效塑性應變兩個變量控制拉伸和壓縮時混凝土的破壞變化。
拉伸等效塑性應變定義為:
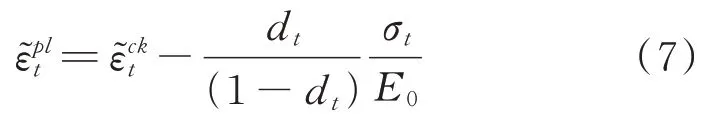
壓縮等效塑性應變定義為:

式中和分別為開裂應變和非彈性應變,=
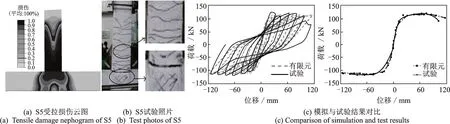
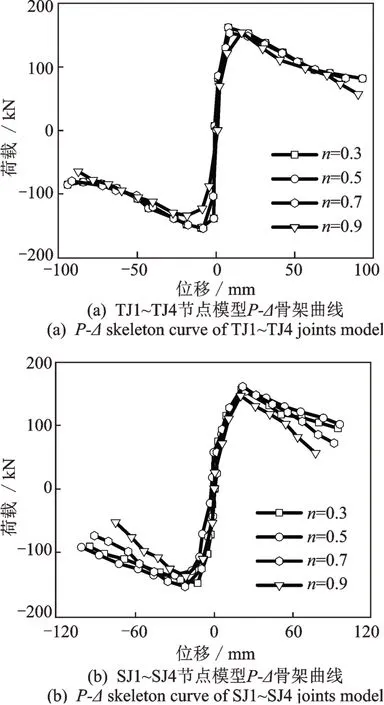
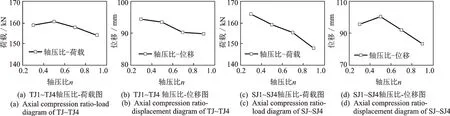
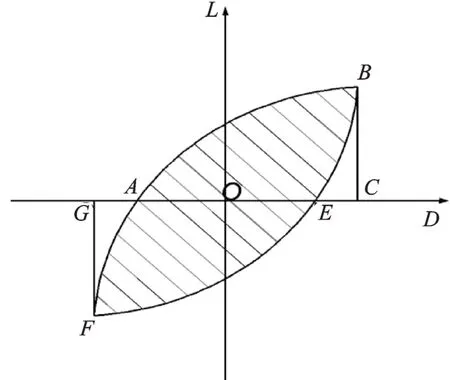
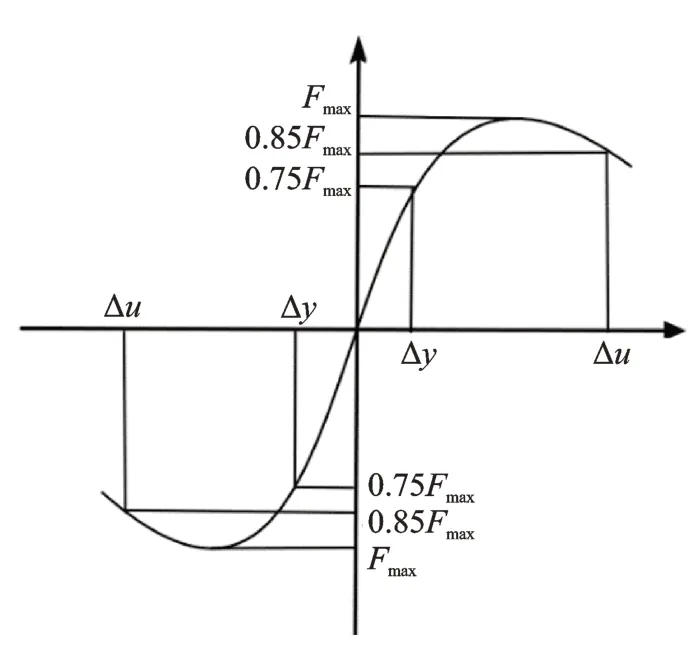
CDP 模型中塑性參數膨脹角ψ是影響混凝土約束效應的重要參數,文獻[14,29]認為纖維混凝土中膨脹角一般取值為30°~40°。偏心率e根據有限元軟件ABAQUS 中規定取默認值0.1 即可。CDP 模型中通過引入黏性參數υ來修正本構模型,黏性參數υ定義了材料的黏塑性規則,一般對于非動力分析,纖維混凝土可取υ=0.0005 以提高數值計算的收斂性[29]。手冊中規定初始等軸壓縮屈服應力與初始單軸壓縮屈服應力之比fb0/fc0取默認值1.16;拉伸子午面上與壓縮子午面上的第二應力之比K手冊中規定為0.5 表3 CDP 模型中的黏塑性參數取值Tab.3 Visco-plastic parameters values in CDP model 2.2.2 鋼筋模型 循環荷載下的節點模型中水泥基材料和鋼筋之間的黏結滑移對計算結果影響較大。引入界面單元和黏結滑移模型需將鋼筋與混凝土之間接觸的部分全部用非線性彈簧連接,而鋼筋與混凝土之間有很多節點,處理不方便、添加起來非常復雜。而QU[15]改進的滯回模型是一種考慮了鋼筋和水泥基材料之間黏結滑移的鋼筋模型,通過減弱鋼筋的卸載剛度來代替鋼筋與混凝土之間因黏結滑移效應而導致的剛度退化,不需引入界面單元。材料模型如圖5所示。 圖5 QU[15]滯回鋼筋模型Fig.5 QU[15]hysteretic reinforcement model 材料模型通過鋼筋的初始彈性模量E0、屈服強度fy、硬化剛度與初始彈性模量的比值α來定義,本研究α取值0.001。由于本研究暫不關注鋼筋與水泥基材料界面間應力發展的情況,所以在保證計算精度一致的情況下,選擇QU[15]滯回鋼筋模型計算效率更高。在有限元軟件ABAQUS 中使用Embed?ded 約束命令將鋼筋內置于混凝土單元內,且模型計算之前調用修正的鋼筋本構模型。 2.2.3 邊界條件及加載制度 實際框架節點中有2 種邊界加載方案[28,30]:(a)在柱端施加循環和軸向荷載,梁端垂直方向固定,符合實際結構中的受力狀態;(b)在柱端施加軸向荷載,梁端施加循環荷載。該加載方案忽略了柱端產生位移時的P?Δ效應。由于本文以節點核心區為研究對象,并且桿端彎矩比、軸壓比及長細比滿足規范規定[10],因此不須考慮P?Δ效應。 在T 型節點中將梁底部設為固定端,在柱頂部施加恒定軸向力以控制軸壓比,并在頂部施加橫向循環荷載。十字型節點通過柱施加循環荷載以及恒定軸向力,柱底部采用不動鉸支座,梁端反彎點提供豎向約束,柱頂采用滾軸支座。 本次采用荷載?位移控制加載方法,首先通過荷載控制,每級循環一次,按照10 kN 遞增。當節點達到屈服荷載時采用位移控制,每級循環2 次,按照10 mm 遞增,一直到試件承載力下降到峰值的85%停止加載。加載制度如圖6所示。 圖6 加載制度Fig.6 Rule of loading 為了驗證有限元模型的可靠性,本文以Yuan等[12]研究的ECC 框架節點(T 型)和梁興文等[13]研究的ECC 框架節點(十字型)試驗數據為基礎,驗證有限元模型的可靠性。 在CDP 模型中引入剛度恢復因子(wt,wc)來描述水泥基材料在循環荷載作用下的剛度恢復和裂縫開閉現象。文獻[31]表明,當混凝土處于壓縮狀態至受拉狀態時,如果在受拉前已形成壓縮微裂縫,混凝土的抗拉剛度恢復很小或不恢復。但當拉伸狀態進入壓縮狀態時,壓縮剛度可以隨著裂紋的閉合而恢復。因此,本文不考慮混凝土抗拉剛度(wt=0 默認值)恢復,而考慮混凝土受壓剛度恢復。李曉琴等[31]提出了一種wc算法,該算法中wc等于單位體積混凝土剩余斷裂能gFR與斷裂能gf之比的θ次方(θ≥1)。 模擬結果(見表4)表明,T 型節點滯回曲線由于考慮了ECC 與鋼筋之間的黏結滑移作用,與試驗結果基本吻合,模擬峰值荷載為128.4 kN,試驗為130.8 kN;模擬屈服位移為10.88 mm,試驗為11.45 mm。十字型滯回曲線模擬峰值荷載為84.65 kN,試驗為80.57 kN;模擬屈服位移為70.81 mm,試驗為73.41 mm,均控制在誤差5%以內。 表4 試驗值與模擬值對比Tab.4 Comparison between test and simulation values 試件S5 與FRCJ4 破壞形態分別如圖7(a),(b)和8(a),(b)所示。S5 裂縫主要分布在框架柱端及節點核心區域。可以看出有限元模型計算結果較好地模擬出試件裂縫分布情況,破壞區域集中在柱端,與試驗結果基本相同。FRCJ4 裂縫主要分布在節點核心區域,核心區域已完全破壞,從有限元模型計算結果中可以看出破壞主要在框架節點核心區,與試驗結果基本一致。圖中當框架節點受拉損傷dt達到0.9 及以上時框架節點核心區域完全破壞。 圖7 S5 框架節點驗證Fig.7 Verification of S5 frame joint 圖8 FRCJ4 框架節點驗證Fig.8 Verification of FRCJ4 frame joint 計算與試驗的滯回曲線與骨架曲線分別如圖7(c)和8(c)所示。計算所得的滯回曲線有明顯的下降段,相對于試驗結果較飽滿,滯回環面積較大。試驗中對梁端反彎點處提供豎向約束,水平方向會產生微小位移;有限元模型中梁端的約束較為理想,邊界剛度較大,對試件的水平運動起到限制作用,使得初始剛度過大。雖然固定約束加強了試件梁端約束作用,但這種影響很小,不會對試驗與模擬結果的位移、承載力及延性等性能產生太大影響,其誤差均控制在5%以內,可以較好地與試驗結果吻合。 綜上,本研究采用的計算模型得到的結果與試驗結果接近,說明該模型具有可靠性,能反映ECC框架節點在低周循環荷載下的受力行為。 以常見的混凝土框架節點為原型進行設計,所有節點均遵循“強柱弱梁”原則,并具體根據規范[10]進行設計,擬采用ECC 替換節點整體區域混凝土做節點模型。本文研究2 種框架節點模型,分別為T型節點及十字型節點。配筋及尺寸均根據規范[10]中的二級抗震等級框架節點的限值進行設計。 T 型節點設計軸壓比為nd=0.3,0.5,0.7,0.9,編號分別為TJ1,TJ2,TJ3,TJ4。在核心處采用箍筋加密處理。十字型節點設計軸壓比同樣為nd=0.3,0.5,0.7,0.9,編號分別為SJ1,SJ2,SJ3,SJ4。具體細節如圖9所示。采用荷載?位移低周循環加載方式進行加載,加載制度同圖6。 圖9 模型尺寸配筋圖Fig.9 Dimension and reinforcement diagram of model 根據混凝土結構設計規范[10],本文基于設計軸力值N設計了4 種軸壓比(對應設計軸壓比nd)的T型和十字型框架節點試件,采用標準軸力值Nk(對應試驗軸壓比nt)進行框架節點受力分析,即采用試驗軸壓比進行有限元計算。其中,設計和試驗軸壓比可根據下式[13]進行換算,試件TJ1~TJ4 和SJ1~SJ4 的參數如表5所示。 表5 試件TJ 和SJ 的參數Tab.5 Design parameters of TJ and SJ 式中nd為設計軸壓比;nt為試驗軸壓比;δc為混凝土強度變異系數,取0.144。 本文采用Li 等[9]通過目標優化得到的ECC 配合比,通過拉伸試驗得到的試驗數據。選用其中X3組,具體參數如表6所示。其ECC 極限拉伸應變達到5.6%,抗拉強度達到3.5 MPa,受拉斷裂能Gf達到5980.43 N/m。 表6 ECC 材料參數[9]Tab.6 Material parameters of ECC[9] 3.2.1 滯回曲線 通過計算得出了T 型節點以及十字型節點模型的破壞形態。其中0.7 軸壓比下2 種節點受拉損傷云圖如圖10 所示。從圖10 中可以看出,十字型節點破壞主要集中在節點核心區和梁柱交界處;T 型節點破壞主要集中在梁端及節點核心區與梁端交界處,其破壞形態均為延性破壞。 圖10 0.7 軸壓比下受拉損傷云圖Fig.10 Tensile damage nephogram under axial compression ratio of 0.7 計算得到的滯回曲線如圖11 所示。在試件加載初期,節點模型處于彈性階段,未達到屈服狀態,卸載之后殘余變形很小,滯回曲線基本為直線狀態。當試件到達塑性階段,開始產生殘余應變,內部損傷開始累積,滯回曲線面積開始增大,耗能能力開始提升。隨著軸壓比的增加,兩種框架節點的耗能能力開始下降,導致滯回環面積變小、不飽滿,出現捏縮現象。低軸壓比下滯回環飽滿,耗能能力強,同一位移處循環曲線接近,剛度和強度退化較小。高軸壓比下滯回環出現捏攏現象,是由于框架節點的抗剪變形產生的斜裂縫張合造成的,滯回環面積小,耗能較差。試件TJ1~TJ4 的滯回環面積與軸壓比呈負相關,并在0.7 軸壓比下梁端發生了嚴重的塑性變形,滯回環開始捏縮。隨著軸壓比的增大,試件SJ1~SJ4 的框架梁端由于承受縱向循環荷載,梁端破壞較為嚴重,滯回環面積與軸壓比呈負相關。同時SJ1~SJ4 的滯回環在同一軸壓比下沒有TJ1~TJ4 的滯回環面積大,說明T 型節點的耗能能力要比十字型節點較好。 3.2.2 骨架曲線 TJ1~TJ4,SJ1~SJ4 的骨架曲線如圖12 所示,T 型邊節點循環荷載施加在框架柱端,更大的軸壓比會施加給框架柱更大的軸向力,限制了柱端的部分位移,所以模型TJ1~TJ4 到達峰值承載力較快,下降趨勢比較平緩,強化階段剛度變化不是很明顯。只是不同軸壓比下承載力和位移變化較顯著。十字型節點循環荷載施加在柱端,框架柱端會產生較大位移,所以模型SJ1~SJ4 相比于TJ1~TJ4 到達峰值承載力的速度有所下降,到達峰值承載力之前會產生較大位移。由于框架節點在高軸壓比下產生了較大的塑性變形,所以軸壓比越大框架節點承載力下降越快,在軸壓比較小時框架節點在強化階段的剛度有較大提升。 圖12 節點模型骨架曲線Fig.12 Skeleton curve of joints model 3.3.1 軸壓比對ECC 節點承載力和位移的影響 軸壓比對T 型及十字型ECC 節點的承載力及位移的影響如圖13 所示。 模型TJ1~TJ4 配筋和尺寸都相同,從圖13(a),(b)可以看出,在軸壓比為變量的情況下,軸壓比在0.3~0.5 之間峰值承載力隨著軸壓比的增大而增大,從154.6 kN 提升到161.1 kN,提升1.45%。軸壓比在0.5~0.9 之間峰值承載力隨著軸壓比增大而減小,從161.1 kN 下降到154.4 kN,降低4.16%。而極限位移一直隨著軸壓比增大而減小,在軸壓比為0.3~0.9 之間時,極限位移從92.9 mm 下降到了89.8 mm,降低3.34%。說明軸壓比在0.5 左右時,試件的承載力較好,軸壓比在0.3 左右時,試件變形能力較好。綜合承載力與極限位移表現情況,在0.5軸壓比下T 型邊節點的抗震能力較好。 同樣,從圖13(c),(d)可以看出,模型SJ1~SJ4在軸壓比0.5 時承載力及極限位移最大;在軸壓比為0.3~0.5 時承載力從158.8 kN 上升到163.69 kN,提高3.08%。極限位移在0.3~0.5 軸壓比之間為遞增狀態,位移從97.6 mm 上升到102.4 mm,提升4.92%。而軸壓比在0.5~0.9 之間極限位移為遞減狀態,從102.4 mm 下降到83.4 mm,降低18.56%。綜合說明在0.5 軸壓比下十字型節點的抗震能力較好。十字型節點發生柱端彎曲破壞,從計算結果中可以看出位移和承載力在0.5 軸壓比附近出現峰值。其主要原因就是2 種框架節點在框架中所處的位置不同,隨著軸壓比變化在循環荷載下節點核心區域傳力機理產生變化,導致承載力與位移變化規律略有不同,抗震性能存在差異。 圖13 節點模型軸壓比-位移/荷載圖Fig.13 Diagram of axial compression ratio,displacement or load of joints model 3.3.2 耗能能力分析 構件的耗能能力是評價抗震性能的一個重要指標,本次使用等效黏滯阻尼系數與累計耗能評價8個模型的耗能能力。其等效黏滯阻尼系數計算公式可以表示為[23]: 等效黏滯阻尼系數計算示意圖如圖14 所示;模型TJ1~TJ4,SJ1~SJ4 的等效黏滯阻尼系數與累計耗能變化如圖15 所示。從圖15 中可以看出,所有試件的位移和等效黏滯阻尼系數成正比,模型通過塑性變形而耗散的能量呈正相關,滯回環面積不斷增大、飽滿。所有模型的等效黏滯阻尼系數與累計耗能隨著軸壓比的增大而降低,但在0.5 軸壓比下兩種節點的耗能能力比其他軸壓比下高。且在同一軸壓比下T 型節點相比于十字型節點耗能能力要高。在0.3~0.9 軸壓比下T 型節點相比于十字型節點的等效黏滯阻尼系數ξ分別增長了25.7%,35.6%,15.4% 和6.3%;累計耗能分別增長了27.2%,33.6%,14.6%和5.3%。可以看出,兩種方法的計算結果大致相同,并且T 型節點的耗能能力在0.5軸壓比下與十字型節點相差最大。 圖14 等效黏滯阻尼系數ξ 計算示意圖Fig.14 Calculation diagram of the equivalent viscous damp?ing coefficient ξ 圖15 等效黏滯阻尼系數與累計耗能Fig.15 Equivalent viscous damping coefficient and total en?ergy consumption 3.3.3 剛度退化分析 構件的塑性變形、裂縫情況等可以用剛度退化來表示。模型中引入損傷因子,可以較好地模擬出模型的剛度退化情況。本次采用割線剛度Ki表示ECC 框架節點的剛度退化,計算公式為[23]: 式中Ki表示第i次循環荷載下的割線剛度;±Pi表示第i次循環荷載下的正、負方向下的峰值荷載;±Δi表示第i次循環荷載下的正、負方向下的峰值位移。 T 型和十字型節點的剛度退化曲線如圖16 所示。由圖16(a)可知,T 型框架節點初始剛度較大,達到了6.84~8.34 kN/mm。ECC 產生細微裂縫并與鋼筋之間產生滑移現象,使得剛度退化較為明顯,框架節點屈服以后剛度退化逐步減小,并無剛度突變出現。隨著軸壓比增大,T 型框架節點延性和承載力降低,導致模型TJ1~TJ2 相比于TJ3~TJ4 初始剛度小。 由圖16(b)可知,十字型框架節點初始剛度相對于T 型節點較小,最大只達到了0.3 軸壓比下的5.87 kN/mm,比T 型節點降低29.6%,并且剛度退化較為平緩。在隨著軸壓比的增大,初始剛度開始降低,但變化趨勢并無明顯差異。由于十字型節點柱端壓彎破壞較T 型節點梁端彎曲破壞嚴重,所以T 型節點的整體剛度退化情況相比于十字型節點好。 圖16 節點模型剛度退化曲線Fig.16 Stiffness degradation curve of joints model 3.3.4 位移延性系數μ的分析 常用位移延性系數μ評價構件延性性能。本文采取國內外常用位移延性系數的計算方法[23],用極限位移Δu和屈服位移Δy的比值進行計算。計算示意圖如圖17 所示,計算公式可表示為: 圖17 位移延性系數μ 計算示意圖Fig.17 Calculation diagram of displacement ductility coeffi?cient μ 式中 Δu為極限位移,取正負方向極限荷載下降到85%時對應的位移;Δy為屈服位移,取正負方向極限荷載的75%時對應的位移。 由于施加了很大的軸向力,框架柱產生的位移很小,導致T 型邊節點試件TJ4 位移延性系數最小,從表7中可以看出,TJ1,TJ2,TJ3 相比于TJ4 位移延性系數分別增長了69.1%,98.9%,45.4%。十字型節點中SJ4 位移延性系數最小,SJ1,SJ2,SJ3 相比于SJ4 位移延性系數分別增長了51.8%,20.3%,14.2%。由于ECC 的高延性的特點,8 個框架節點μ全部大于2.9。但由于在高軸壓比下T 型框架節點發生了嚴重的梁端彎曲破壞,導致框架節點梁端產生了嚴重的塑性變形,所以在三級抗震等級下軸壓比要嚴格小于0.9。十字型節點在0.7~0.9 軸壓比下框架柱端發生了嚴重的柱端壓彎破壞,由于框架柱端既承受水平循環荷載,又承受軸向荷載,導致框架節點承載力大幅度下降,在地震作用下會使框架結構抗坍塌能力下降,建議設計軸壓比對2 種類型ECC 框架節點均應控制在0.3~0.7 之間。 表7 各模型位移延性系數Tab.7 Displacement ductility coefficient of each model (1)兩種常見的T 型和十字型ECC 框架節點在設計軸壓比(0.3~0.9)之間位移延性系數μ隨著軸壓比提升而下降。 (2)T 型ECC 節點在軸壓比為0.5 時出現了峰值承載力與位移延性系數的極值點,但極限位移始終與軸壓比呈負相關。且當軸壓比達到0.9 時,構件延性已經不能滿足節點抗震的基本要求。 (3)十字型ECC 節點的峰值承載力、位移延性系數以及極限位移均在軸壓比為0.5 時出現了極值點。在一定范圍內增大軸壓比(0.3~0.5)可以使得十字型框架節點承載力提升,但過大的軸壓比會降低構件延性。 (4)T 型與十字型框架節點的耗能能力特征值,即等效黏滯阻尼系數ξ,隨著軸壓比(0.3~0.9)增大而下降,T 型節點ξ比十字型節點增長約6.3%~35.6%,T 型節點的耗能能力要優于十字型節點。軸壓比對2 種框架節點的剛度退化影響較小,T 型節點的初始剛度為6.84~8.34 kN/mm,十字型的初始剛度為5.87~6.56 kN/mm,T 型節點在屈服前的剛度退化較十字型節點嚴重,耐損傷能力相比十字型節點較差。 (5)兩種節點均在設計軸壓比為0.7 時發生了界限破壞,為保證構件具有一定的抗倒塌能力以及在地震作用下發生延性破壞,超出彈性極限仍具有足夠變形能力,本文建議2 種二級抗震等級下的ECC 框架節點設計軸壓比均應控制在0.3~0.7 之間,且不應超出0.9。并且2 種ECC 框架節點的延性、耗能及剛度退化在0.5 軸壓比下出現最優值(軸壓比為0.3~0.9 時)。因此,本文建議在不影響結構設計的情況下將ECC 框架節點的設計軸壓比控制在0.5 時抗震性能可處于較優狀態。


2.3 試驗/模擬結果比較


3 不同軸壓比下ECC 框架節點抗震性能分析
3.1 ECC 框架節點模型設計及抗震模擬分析


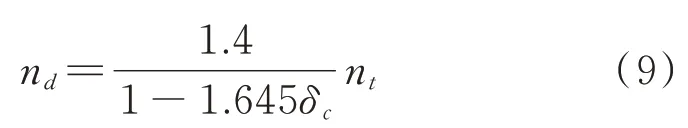

3.2 不同軸壓比下ECC 節點抗震模擬結果

3.3 ECC 框架節點抗震性能分析






4 結 論

