回歸分析在順逆流糧食干燥機干燥過程建模中的應用

◎ 王 赫

（遼寧省糧食科學研究所，遼寧 沈陽 110032）

糧食干燥是糧食儲藏的第一道關鍵性作業程序，干燥技術工藝形式較多。由于糧食干燥系統是大時滯、多干擾強的非線性系統，長期以來自動化程度低，干燥作業過程中控制的嚴重時滯和干燥結果的不可調整性沒有解決[1]。糧食干燥機是一個開放式熱力學系統，干燥機內溫度變化規律將是內部狀態變化可觀測的指標。通過研究干燥過程糧食通過各溫度段的變化規律，對實現干燥過程工藝參數的實時控制，及時調節干燥工藝參數具有重要意義[2]。

20世紀90年代以來，隨著我國科技能力的大大提高，農業現代化的全面展開，糧食干燥機行業也初具規模，我國生產的糧食干燥機從技術、性能、品牌等方面均已得到相當大的提升。就順逆流連續式烘干機而言，各項技術工藝日漸成熟完善[3]。因此本文通過采集順逆流糧食干燥機干燥過程試驗數據，分析干燥過程參數，解決糧食干燥過程參數控制，建立順逆流糧食干燥機玉米干燥過程回歸預測模型，為糧食干燥過程提供指導。

1 材料與方法

1.1 試驗材料

玉米：遼寧省建平市當地、當年產玉米。

1.2 試驗設備

順逆流糧食干燥機由鐵嶺凱瑞烘干設備有限公司生產，型號為HGT-300，日處理量300 t·d-1。本設備主要由干燥塔體、供熱、輸送、電控等配套設備組成。通過在入糧口、熱風管道處、冷風管道處、排糧口及干燥機內部安裝溫度傳感器，建立糧食干燥智能溫度監測及數據采集系統，圖1為順逆流糧食干燥機裝置圖。

圖1 順逆流糧食干燥機裝置圖

1.3 試驗方法

本試驗研究順逆流糧食干燥機玉米干燥過程，通過糧食干燥智能溫度監測及數據采集系統連續檢測并每隔10 min記錄一次干燥過程中熱風溫度、干燥機內玉米緩蘇溫度及冷卻溫度，每隔1 h通過人工化驗記錄玉米入機糧及出機糧含水率，除檢測溫度外，通過干燥機上部原有安裝的料位計檢測并計算實際的糧食排放速度，記錄排糧頻率。

2 建立糧溫回歸分析模型

回歸分析是研究現象之間存在的相互關系的方法，通過確定兩種或兩種以上變量間的因果關系，建立回歸模型。根據實測數據求解模型的各個參數，評價回歸模型是否能夠很好地擬合實測數據，如果能夠很好地擬合，則可以根據自變量作進一步預測。回歸分析可以通過一個數學模型來表現現象之間相關的具體形式[4]。如果回歸分析中包括兩個或兩個以上的自變量，且因變量和自變量之間是線性關系，則通過多重線性回歸分析來處理一個因變量與多個自變量之間的線性關系，建立變量之間的線性模型并根據模型進行評價和預測[5]。

2.1 多重線性回歸分析模型的一般形式

多重線性回歸是指包含兩個或兩個以上因變量的線性回歸模型。所以，多重線性回歸模型為

式中：Y為因變量；Xn為第n個自變量；a為常數 項，是回歸直線在縱坐標軸上的截距；bn為第n個偏回歸系數；ε為隨機誤差，即隨機因素對因變量所產生的影響。

偏回歸系數bn表示在其他自變量保持不變時，自變量Xi每變動一個單位所引起的因變量Y的平均變動的單位數[6]。

2.2 排糧頻率與糧溫的回歸分析

在很多回歸分析問題中，上述多項式模型被廣泛應用。本文取式（2）作為排糧頻率與糧溫的回歸模型：

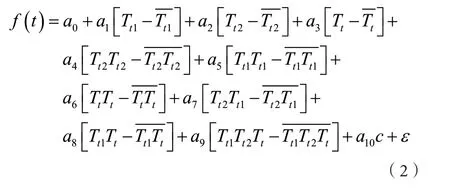
式中：f為排糧頻率；t為時間；Tt為當前時刻糧溫；Tt1為提前2 h的糧溫；Tt2為提前4 h的糧溫；a0…a10為未知常量參數；等類似的變量表示取該變量所有試驗樣本數據的平均值，ε服從正態分布N(0,σ2)。

公式（2）是一個多元多項式，可以通過變量代換線性化。

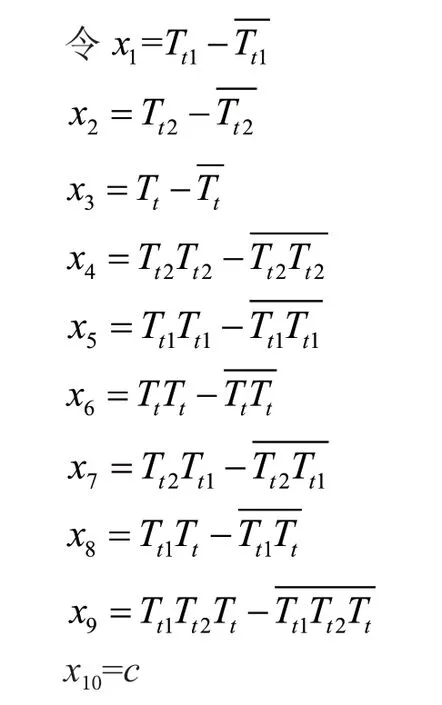
則該多元多項式回歸模型就轉換為多元線性回歸模型：

本文使用最小二乘法估算相應的偏回歸系數。

通過整理玉米原始干燥記錄，選取連續120 h的玉米干燥數據作為樣本，取得120組觀測值(xi1,xi2,xi3,xi4,xi5,xi6,xi7,xi8,xi9,xi10;yi)，其中i=1,2,…,120。本文通過MATLAB軟件編程進行數據的分析與擬合，得到了排糧頻率與糧溫非線性回歸模型中的各個回歸系數的值。a0=y-，表示以上樣本排糧頻率的平均值，公式（2）即為當前樣本排糧頻率的值等于a0的基礎上，根據各回歸系數調整糧食溫度偏差值所得到的。排糧頻率與糧溫的回歸模型為

根據該模型，圖2給出了排糧頻率與糧溫的關系曲線。從圖中可以看出，隨著玉米溫度的升高，排糧頻率升高。這與工人現場根據糧溫調整排糧頻率的經驗符合。

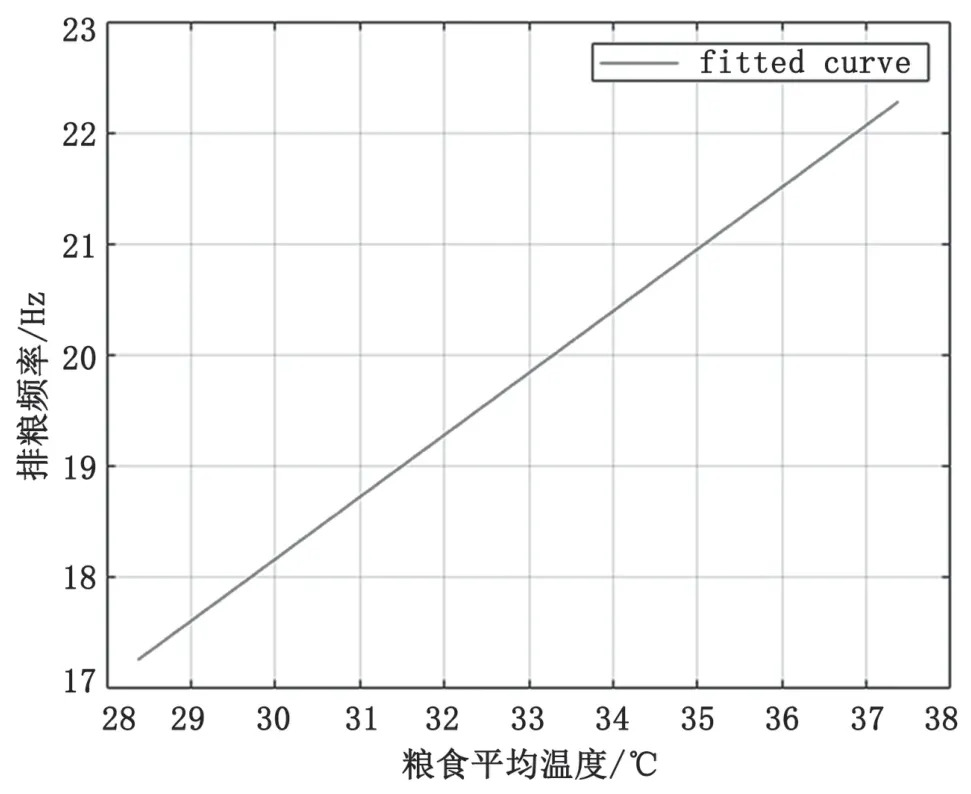
圖2 排糧頻率與糧溫關系曲線圖

根據回歸模型可提前4 h預測排糧頻率，圖3為樣本排糧頻率預測值與實測值比較曲線。可以看出，預測的結果與實際的結果十分相近，說明該模型有較好的回歸效果。

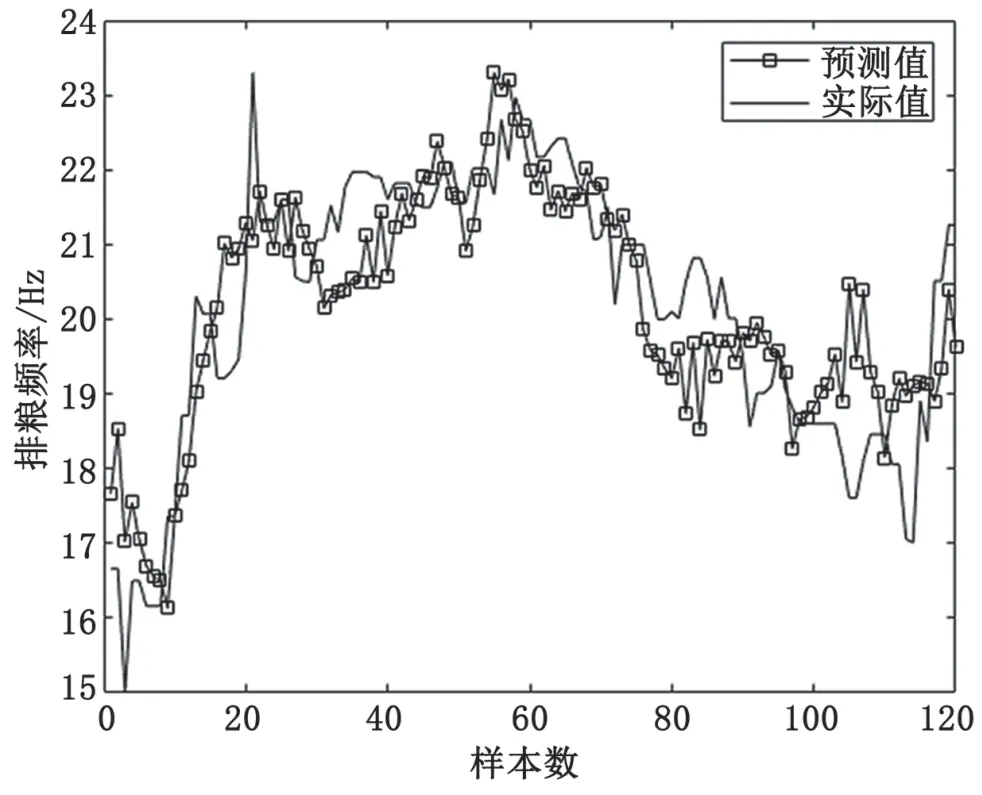
圖3 排糧頻率實際值與預測值對比圖

2.3 樣本出機含水率與糧溫的回歸分析

公式（5）作為樣本出機含水率與糧食高低溫度的回歸模型[7]：

式中：W為出機樣本含水率；b0,…,b28為未知常量系數；Tt1為前i×2 h的糧食樣本高溫溫度；Tt2為前i×2 h的糧食樣本低溫溫度；ε為隨機誤差；表示取該變量所有試驗樣本數據的平均值，ε服從正態分布N(0,σ2)。

公式（4）是一個多元多項式，同上可以通過變量代換線性化。

則該回歸模型就轉換為多元線性回歸模型：

同上使用MATLAB軟件編程進行數據的分析與擬合，得到了樣本出機含水率與糧溫回歸模型中的各個回歸系數的值，其中，，由于b0表示樣本出機含水率的平均值，因此公式（5）即為當前樣本出機含水率的值等于b0的基礎上，根據各回歸系數調整糧食溫度偏差值所得到的。表1為求得的b0,…,b28的值。

表1 樣本含水率與糧溫回歸模型系數表

通過以上計算，將表1所得的回歸系數代入公 式（5），即可求得糧食高低溫度與樣本出機含水率的非線性回歸模型。根據該模型，繪制樣本出機糧含水率與標準值之差與糧食高低溫度的三維關系圖，見圖4。 在高溫干燥段，出機糧含水率隨著溫度升高而降低，在低溫干燥段，出機糧含水率隨著溫度升高而升高。

圖4 糧食高低溫度與樣本出機含水率的關系圖

利用該回歸模型，可以提前預測出機糧含水率。圖5為樣本出機含水率預測值與實測值比較曲線。可以看出，預測的結果與實際的結果十分相近，可以指導糧食干燥過程。

圖5 出機糧含水率預測值與實測值比較曲線圖

3 結論

本文通過采集玉米干燥過程實際生產數據作為研究樣本，分析干燥參數，建立樣本排糧頻率及出機含水率與糧食溫度的在線回歸預測模型。經驗證該模型可有效預測糧食樣本出機糧含水率，為工人調整生產過程中的排糧頻率提供指導意見。