基于預測校正的落角約束計算制導方法

劉子超，王江，何紹溟,*，李宇飛

1. 北京理工大學 宇航學院，北京 100081 2. 北京理工大學 無人機自主控制技術北京市重點實驗室，北京 100081 3. 北京理工大學 信息與電子學院，北京 100081

隨著現代防御技術的發展，裝甲車輛、艦船、防御工事等目標的防御能力顯著提升。當導彈以一定的角度命中這類目標時，能夠得到更好的打擊效果，因此一些制導律的設計中引入了落角約束。Ryoo等基于能量最優性能指標，選取剩余飛行時間的函數為性能指標的權函數，推導了最優落角約束制導律。張友安等應用Schwarz不等式求解了有無控制系統動力學情況下最優制導律的一般表達式。Erer等在比例導引律的基礎上附加角度約束偏置項，通過偏置項縮小落角誤差，實現落角控制。Liu等針對使用脈沖發動機控制的飛行器，提出了帶角度約束的最優脈沖制導律。Park等選取剩余飛行距離的函數為性能指標的權函數，推導了帶視場角約束的落角約束制導律。郭建國等將終端攻擊角度約束轉化為終端視線角約束，利用螺旋控制算法設計了一種二階滑模變結構制導律。He等建立了時變加權視線角誤差動力學，基于李雅普諾夫穩定性理論設計了滑模制導律。Kim等則在落角約束問題的基礎上引入了視場角約束，提出了不依賴相對距離與視線角變化率的滑模制導律。在具有落角約束的制導律設計中，應用最多的是最優控制和滑模變結構控制思想。但是最優制導律對假設條件依賴性強，魯棒性較差，滑模制導律又容易發生抖振，如何提高落角約束制導律的魯棒性和穩定性仍然是飛行器制導系統設計的關鍵問題。

隨著計算機技術的快速發展，幾乎所有學科都走向定量化和精確化，從而產生了一系列計算性的學科分支。在飛行器制導控制領域，計算制導也獲得了越來越多的關注。傳統制導研究一般需要引入一些假設條件來推導解析制導律，例如常值速度假設，并且無法處理復雜的制導問題；而計算制導一般不依賴假設條件簡化制導問題，而是使用數值計算方法生成制導指令，偽譜法制導以及深度學習制導都屬于計算制導。

根據系統模型在計算制導中的應用，可以將計算制導算法分為兩類：① 基于模型的計算制導算法；② 基于數據的計算制導算法。基于模型的計算制導采用參數化方法將連續空間的最優控制問題求解轉化為非線性規劃問題，通過數值計算求解規劃問題獲得最優解；基于數據的計算制導方法則是以深度學習為主要工具，從飛行數據中學習制導指令或系數與飛行狀態之間的映射關系，根據飛行器的飛行狀態動態調節制導指令，從而使飛行器狀態收斂至期望的約束。

隨著人工智能技術的發展，深度學習在制導控制領域的應用備受關注。深度學習計算量相對更少，能夠提高計算制導的實時性，并且對非線性函數具有良好的擬合能力，因此近幾年學者們對深度學習在制導控制領域的應用開展了大量研究。方科等使用深度監督學習根據當前飛行狀態預估到達時間，然后根據時間誤差對視線角走廊進行動態調整，該方法調整形式較為簡單，但是沒有考慮最優性指標。Shalumov使用深度強化學習設計了突防制導律，結合滑模制導的思想，學習制導律的切換策略。余躍和王宏倫使用深度監督學習處理傳統預測校正制導算法的實時性問題，使用深度神經網絡代替傳統算法對導彈運動微分方程組的積分，提高了算法的實時性。Furfaro等使用深度強化學習訓練制導律的系數，實現再入飛行器軟著陸，但是整條彈道的獎勵值需要在得到終端狀態之后才能進行計算，存在稀疏獎勵問題，初期收斂速度較慢，訓練效率較低。

本文基于預測校正制導思想，結合監督學習和深度學習，提出了一種基于學習的計算制導方法(Learning-based Computational Guidance, LCG)。該方法首先訓練深度監督學習預測落角，然后以偏置比例導引法為基礎，使用深度強化學習輸出偏置項，使預測落角向期望落角收斂。本文的主要貢獻如下：① 提出了一種新的計算制導框架，該框架除了解決落角約束以外，能夠推廣應用于其它約束條件，如飛行時間約束，落速約束等；② 使用深度監督學習實時預測終端狀態后引入深度強化學習模型中，解決了深度強化學習模型的稀疏獎勵問題，提高了訓練效率；③ 針對落角控制問題設計了考慮最優性指標的強化學習獎勵函數，降低了能量消耗。

1 問題描述

針對二維平面下導彈攻擊固定目標的落角約束問題建立彈目相對運動的數學模型，如圖1所示。圖中：為導彈飛行速度，為彈道傾角，、、分別表示升力、阻力、重力；為彈目視線角；為彈目相對距離；表示彈道軌跡。

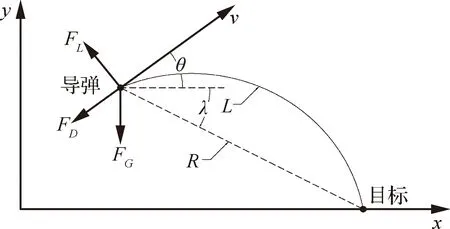
圖1 彈目相對運動模型Fig.1 Relative motion model of missile and target

導彈的運動學微分方程如下

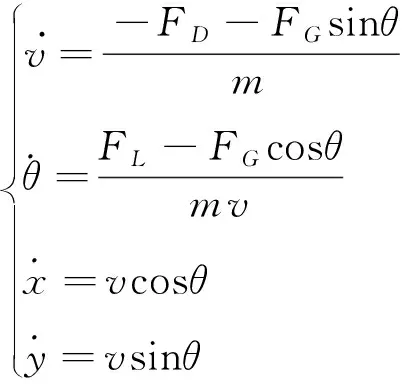
(1)

式中：(,)表示導彈在平面中的位置；為導彈質量。各氣動力為

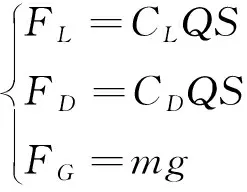
(2)

式中：為升力系數；為阻力系數；為導彈的參考面積；為重力加速度；表示動壓:

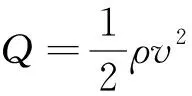
(3)

其中：為空氣密度。

在導彈飛行過程中，攻角一般較小，氣動系數可近似表示為

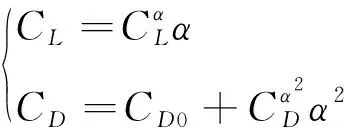
(4)

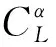
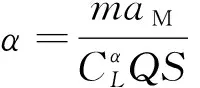
(5)

為了滿足落角約束，導彈的終端位置與彈道傾角應當滿足如下關系

=,=,=

(6)

式中：下標f表示終端狀態；下標d表示期望狀態。

雖然本文仿真模型以及方法設計基于二維縱向平面開展，但是本文提出的方法可以應用于三維場景。在三維場景中，滾轉穩定導彈的制導問題可以分解至水平通道和垂直通道，解耦為兩個獨立的問題并分別進行分析。將本文的訓練結果應用于二維縱向平面，然后將訓練場景更換為水平通道，使用本文設計的算法訓練適用于水平通道的模型，即可在三維場景的兩個通道分別使用兩個計算制導模型，實現三維場景制導。

2 帶落角約束的計算制導框架

本文設計的LCG框架以偏置比例導引律為基礎，偏置比例導引律一般具有如下形式

=+

(7)

式中：為比例導引制導律(Proportional Navigation Guidance, PNG)，負責縮小導彈的零控脫靶量(Zero Effort Miss, ZEM)；為偏置項，負責使預測落角收斂至期望落角。為了抵消重力的影響，中引入了重力補償，表示為

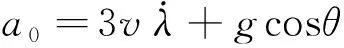
(8)

引入落角約束后，LCG框架如圖2所示。該框架由兩部分組成：深度監督學習預測模塊(Deep Supervised Learning Module, DSLM)與深度強化學習校正模塊(Deep Reinforcement Learning Module, DRLM)。在學習階段，首先通過離線采集的標注數據訓練DSLM，令DSLM學習飛行狀態與落角之間的映射關系；當DSLM訓練完成后，即可實時預測落角誤差，令DRLM通過仿真飛行實驗與導彈試錯交互，使用交互生成的數據訓練DRLM，改進偏置項的生成策略。當DRLM訓練完成后，即可結合DSLM預測的落角誤差實時動態地調節偏置項，使落角誤差收斂。

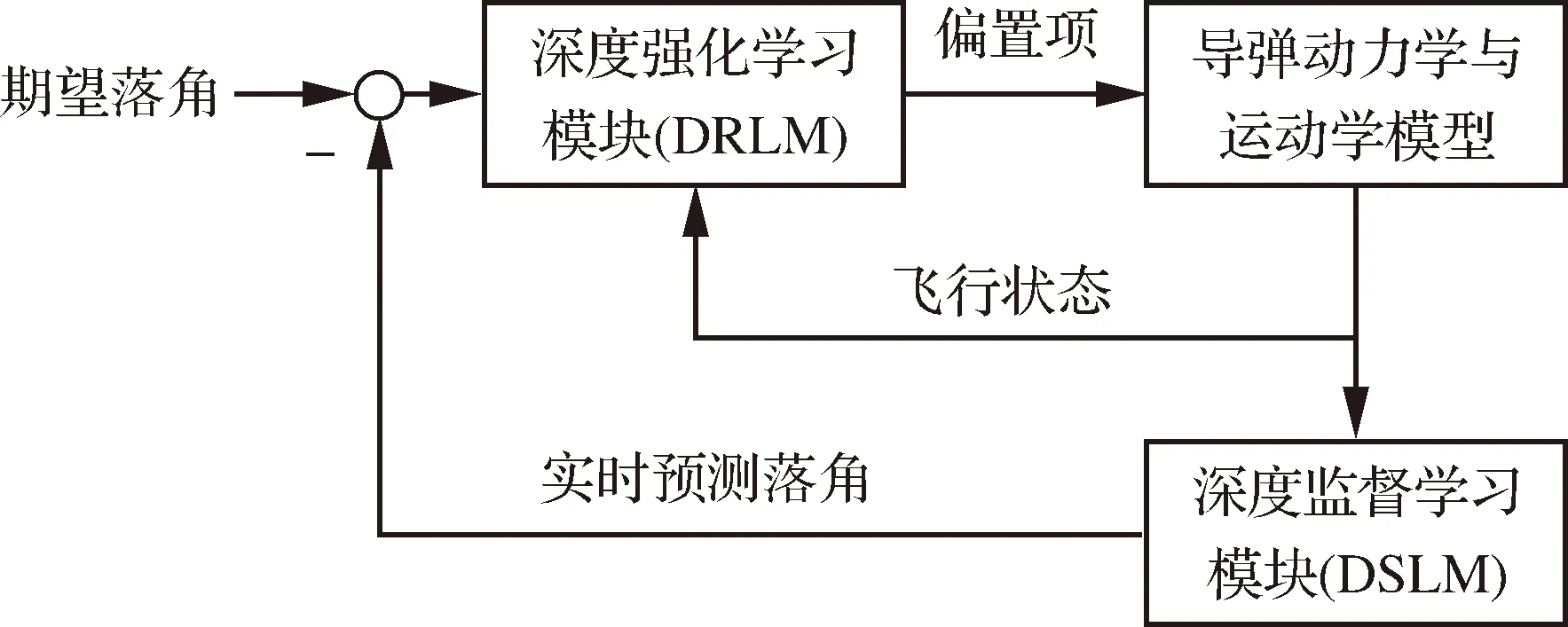
圖2 帶落角約束的計算制導框架Fig.2 Framework of learning-based computational guidance with impact angle constraint

在傳統的預測校正制導中，預測模塊使用彈道積分，根據導彈的當前狀態預測終端狀態，然后校正模塊根據預測值與期望值的偏差調整控制指令，使偏差逐漸收斂。本文所提出的算法基于預測校正思想設計，其中DSLM根據飛行過程中實時變化的狀態在每個周期預測終端落角，計算落角誤差；DRLM根據落角誤差生成制導指令并執行后，DSLM再基于新的狀態預測落角。

訓練DSLM使用的離線標注數據按照如下方式采集。首先令式(7)中的=0，制導律即退化為PNG。如果目標靜止或機動形式已知，不考慮環境帶來的擾動，一組發射狀態生成的彈道具有唯一性，彈道上任意一點的飛行狀態已知時，這條彈道對應的落角即可唯一確定；如果目標機動形式未知，隨著導彈剩余飛行時間縮短，目標的機動范圍逐漸縮小，落角預測誤差隨之收斂；由于DSLM使用飛行過程中的狀態預測落角，不存在誤差累積問題，當環境存在偏差或模型不準確時，落角預測誤差也會隨著導彈剩余飛行時間的縮短而收斂。在DSLM的訓練數據采集階段，以PNG為制導律，引入氣動系數攝動，通過蒙特卡洛實驗獲取大量彈道數據，然后將飛行狀態標注為輸入數據，將終端狀態標注為輸出數據。

DRLM將制導模塊視為智能體，將智能體以外的其它部件統一視為環境。智能體以導彈的飛行狀態為輸入，以偏置項為輸出，以獲得最大的總環境獎勵值為目標，在與環境的試錯交互中不斷改進制導策略；環境獎勵根據預測誤差及其它約束項計算得出。相比傳統方法，DRLM不需要求解制導指令與約束項之間的解析關系，因此不依賴假設條件來簡化模型，也可以將一些過程約束引入制導律設計中。

與其它計算制導算法相比，基于預測校正制導思想的計算制導方法能夠更好的適應訓練模型偏差。這是因為預測校正制導對初始誤差不敏感，同時校正模塊中實時生成的校正指令也能對模型偏差引起的預測角落誤差進行校正。因此本文設計的LCG框架具有較好的抗擾性、魯棒性和自適應能力。

3 深度監督學習預測模塊

傳統的預測校正制導中，預測模塊對運動學方程進行大量的數值積分，實際應用時存在實時性問題。深度監督學習的計算速度更快，輸入當前狀態即可實時預測落角，能夠顯著提高算法的實時性。

3.1 DSLM結構設計

DSLM使用具有多個隱層的神經網絡，基于標注數據通過一定的訓練方法擬合輸入數據與輸出數據之間的映射關系。典型的多隱層神經網絡由輸入層、輸出層、以及多個隱層構成，每個隱層中包含了大量的神經元。DSLM使用的神經網絡的結構如圖3所示。

假設第層具有個神經元，+1層具有個神經元，則每個層的神經元執行的計算如式(9) 所示:

=()∈{1,2,…,}

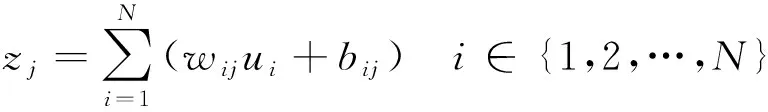
(9)

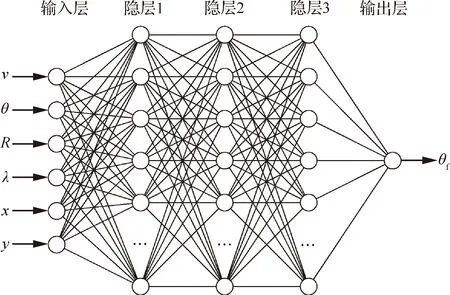
圖3 DSLM的網絡結構Fig.3 Network structure of DSLM

式中：為單個神經元的輸入；為單個神經元的輸出；為中間變量；為神經元的權重；為神經元的偏移量；{,,…,}構成了第+1層的輸入；{,,…,}為第+1層的輸出；下標表示數據來源于第層的第個神經元，下標表示數據在第+1層的第個神經元中計算；(·)是激活函數。

當前神經網絡的輸出層設計為落角，輸入層設計為飛行狀態向量(,,,,,)。其中：和表示導彈在平面中的絕對位置，與、一同表征導彈自身的當前飛行狀態；、表示當前彈目相對狀態。在飛行過程中，這些飛行狀態一般可通過彈載傳感器或導引頭獲得。

本文設計的神經網絡使用3個全連接層作為隱層，每層有100個神經元。使用線性整流單元(Rectified Linear Unit, ReLU)作為輸入層和隱層的激活函數，輸出層不設置激活函數。ReLU的形式為

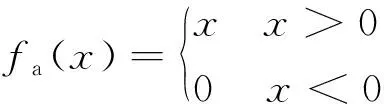
(10)

3.2 DSLM學習過程

DSLM的訓練一般需要大量的標注數據樣本。以PNG為制導律，對式(1)進行數值積分，通過蒙特卡洛仿真生成足夠多的彈道數據，在仿真過程中引入氣動系數隨機攝動，使訓練樣本覆蓋更大范圍的樣本空間。在本文設定的場景中，使用PNG攻擊固定目標時不會發生脫靶現象。當導彈滿足≤時，即為完成一次仿真飛行實驗，為最大脫靶量。

第次仿真飛行實驗完成時，彈道對應的落角隨即獲得，以彈道上的所有飛行狀態向量為輸入，對應的輸出標注為，作為一系列標注數據樣本。

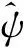
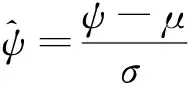
(11)

當樣本采集完成后，將樣本中2%的數據劃分為測試集，2%的數據劃分為驗證集，剩余96%的數據作為訓練集。令=[,]，定義損失函數為網絡參數的函數

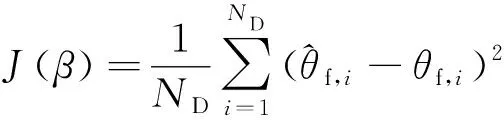
(12)

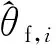
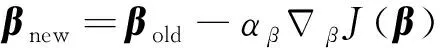
(13)

式中：為學習率，在訓練前人為設定初值，訓練過程中，ADAM優化器會自適應地動態調節學習率。

4 深度強化學習校正模塊

本文設計的DRLM使用近端策略優化算法(Proximal Policy Optimization, PPO)。PPO具有兩個神經網絡，分別為策略網絡和評價網絡。策略網絡表示當前狀態與指令之間的映射關系；評價網絡估算當前狀態的潛在價值，然后結合已實施的指令獲得的獎勵值序列，計算這些指令的獎勵相對于潛在價值的優勢函數。當優勢函數為正，則增大已實施指令在策略中的概率；當優勢函數為負，則減小這些指令的概率。為了減小訓練過程的波動，更新策略時還需要確保新舊策略之間的差異較小。

4.1 落角約束問題的強化學習模型

在強化學習模型中，智能體以試錯的方式進行學習，與環境交互后獲得獎勵，以最大化總環境獎勵值為目標，學習當前狀態下的最優控制指令。強化學習過程可用時間序列={,,,…}表示，={,,}。其中：為環境在時刻的狀態；為智能體在時刻所采取的行為；為在時刻環境給出的獎勵。在下一時刻，智能體將作用于環境，環境隨即給出獎勵+1，并從狀態變為+1。在應用強化學習算法前，首先需要針對落角約束問題定義智能體與環境交互的接口，即狀態、行為、獎勵。

將DRLM的行為定義為式(7)中的偏置項。在試錯訓練初期可能會產生過大的偏置項，致使導彈脫靶，因此需要對偏置項進行限幅為

=||≤

(14)

式中：為偏置項的限幅。

策略網絡以為輸入，為輸出。為了設計狀態，首先分析與存在相關關系的變量。彈道可以表示為導彈運動方程組的積分，積分時間即為導彈的剩余飛行時間。當導彈與目標之間距離較遠時，積分時間較長，導彈能夠以較小的實現落角控制；當縮短，導彈需要使用更大的才能糾正同等的落角誤差。因此，與存在負相關關系；預測誤差與顯然是正相關的，越大，需要的也越大。因此將狀態設計為

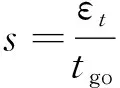
(15)

對獎勵的設計是最重要的，因為合理能夠確保學習過程收斂，并且能夠提高學習效率。除了落角約束，導彈還需滿足一些額外的約束來滿足最優性指標。不同約束可能具有不同的非線性形式，首先使用指數函數將不同約束的尺度統一，然后賦予不同的權重來調節各約束的對智能體的影響。獎勵的形式為

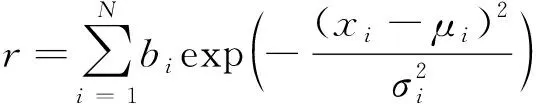
(16)

式中：為權重系數；為約束項；為偏移系數；為縮放系數；下標表示第項約束。其中滿足

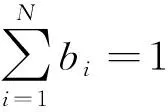
(17)

訓練好的DSLM給出了預測落角，結合期望落角即可計算預測的落角誤差。文獻[25]提出了預測校正制導中誤差動力學的最優收斂形式。最優誤差動力學定義為

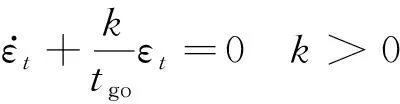
(18)

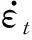
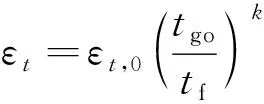
(19)

式中：,0表示誤差的初值。當=0時，=0。誤差動力學式(18)能夠最小化一些性能指標，為了模擬最優誤差動力學，針對落角約束的獎勵項設計為式(20)的形式。

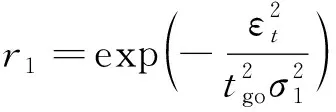
(20)

其中：為落角約束的縮放系數。

根據能量守恒定律，在飛行期間執行機動消耗的能量越少，擊中目標時的動能越大，攻擊效果越好，因此需要對機動的能量消耗進行約束。在最優控制中，能量消耗的目標函數一般設計為

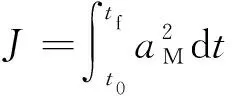
(21)

計算狀態的潛在價值時隱含了對獎勵的積分，因此可以將該約束項設計為

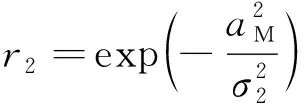
(22)

式中：為能量消耗約束的縮放系數。

結合式(20)和式(22)，引入各約束項的權重，獎勵值即為

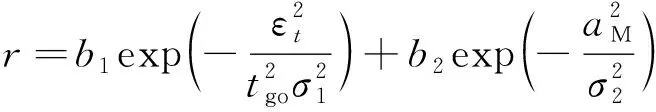
(23)

將落角約束問題抽象為強化學習問題后，行為、狀態、獎勵如式(14)、式(15)和式(23)所示。為了加強終端落角與脫靶量在訓練過程中的影響，在仿真飛行實驗完成時，調節最后一個周期的獎勵值

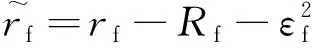
(24)

式中:為脫靶量；為終端落角誤差。

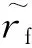
4.2 近端策略優化算法

PPO是一種基于策略的深度強化學習算法。策略可定義為智能體在不同狀態下的各種行為的概率分布，用(|)表示。PPO將行為視為隨機變量，該隨機變量服從一定的概率分布，概率分布的參數由PPO中的策略網絡輸出，行為從這一概率分布中隨機選取。PPO的網絡結構如圖4所示。

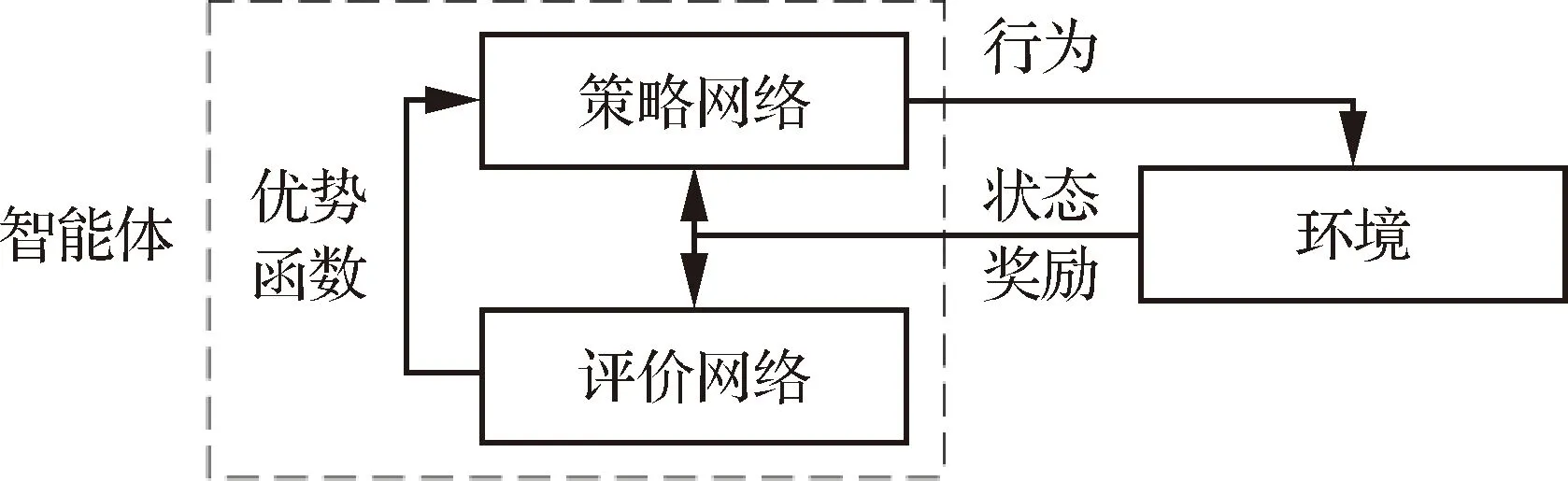
圖4 PPO的網絡結構Fig.4 Network structure of PPO

1) 評價網絡

PPO的目標是尋找一個策略，使智能體在未知環境中獲得最大的總環境獎勵值，但是總環境獎勵值一般無法直接計算。在離散系統中，總環境獎勵值具有如下形式

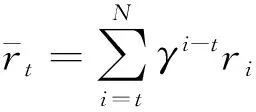
(25)

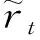
為了表示不同狀態下的總環境獎勵，用數學期望的形式定義的狀態值函數()，表示狀態的潛在價值:

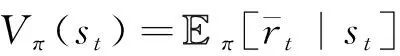
(26)

為了評估行為的優劣，一些強化學習算法定義了在狀態下行為的行為值函數(,)，表示行為的潛在價值:

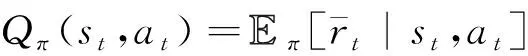
(27)

()可用(,)表示為

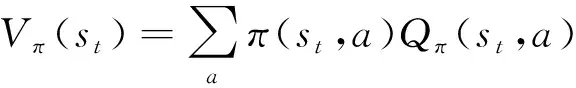
(28)

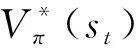
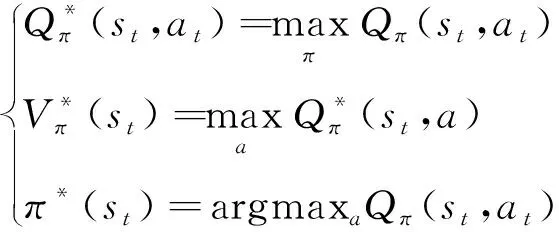
(29)

(,)=(,)-()

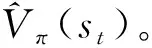
(30)

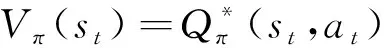
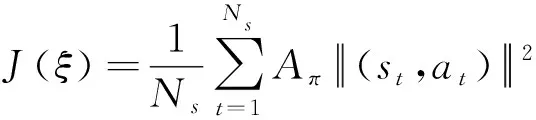
(31)

式中：為評價網絡的參數。

參數更新如式(32)所示:

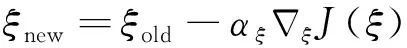
(32)

式中：為評價網絡的學習率。

但是優勢函數中的兩個值函數仍然是無法直接計算的，使用多步估計法估算優勢函數，表示為

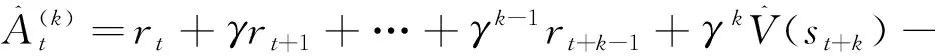
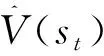
(33)

式中：為估算步長，與交互樣本量相關。

2) 策略網絡

策略網絡以狀態為輸入，以策略的參數為輸出。一般使用高斯分布作為策略的概率分布，策略網絡的輸出即為高斯分布的均值和標準差。PPO是基于置信域策略優化算法(Trust Region Policy Optimization, TRPO)改進設計的，在TRPO中，策略網絡的目標函數為

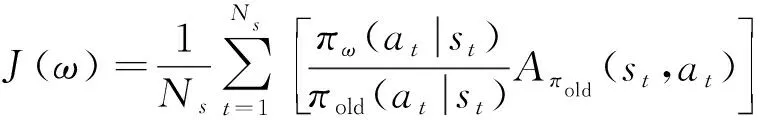
(34)

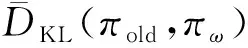
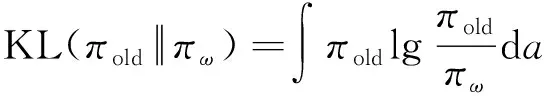
(35)

根據式(30)，優勢函數(,)表示當前行為值函數相對于當前狀態值函數的優勢，若優勢函數為正，則應當提高當前行為在策略中的概率；反之，若優勢函數為負，則需要降低當前行為在策略中的概率。TRPO通過最大化目標函數實現了這一過程，并且使用限制了策略更新幅度的上界，提升了策略更新過程的穩定性。但是KL散度的計算量仍然較大，而且TRPO在更新策略時還使用了共軛梯度法等方法，工程實現較為不便。

PPO簡化了TRPO的計算，使用剪切函數約束策略的更新幅度。PPO的目標函數為

() =

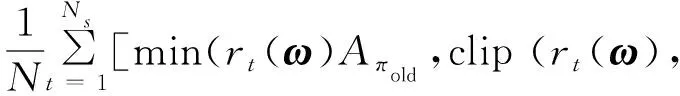
(36)

式中：()表示比率函數，

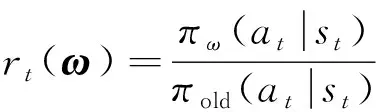
(37)

clip((),?)表示剪切函數，為

clip ((),?)=

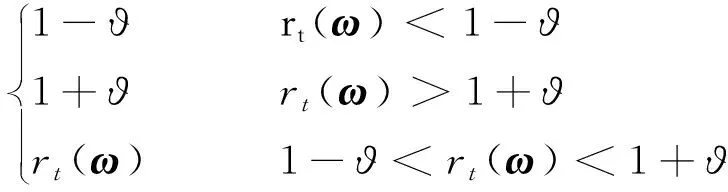
(38)

式中：?為約束策略更新幅度的剪切參數。

由式(38)可見，剪切函數將新舊策略的比率約束在(1-?,1+?)內，隨即約束了新策略的更新幅度。策略網絡參數的更新公式為

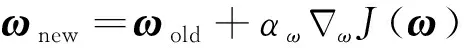
(39)

式中：為策略網絡的學習率。

4.3 網絡結構與學習過程

本文使用的PPO中，策略網絡和評價網絡均均由4個全連接層組成，使用了2個隱層，各層維度如表1所示。除了輸出層，其它各層均使用ReLU作為激活函數。策略網絡的輸出層使用兩種不同的激活函數，均值輸出使用的激活函數tanh為

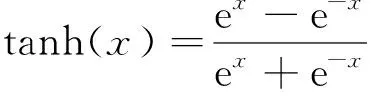
(40)

tanh函數能夠將網絡的輸出限幅至[-1,1]。將輸出層的輸出乘以式(14)中的，即可將策略網絡輸出的均值限制在[-,]之間。

標準差輸出使用的激活函數為softplus，形如式(41)。Softplus函數的輸出恒大于0，滿足標準差的物理意義。

()=ln(1+e)

(41)

本節的強化學習與3.2節的監督學習獲取樣本的方式有一定區別。監督學習的樣本采集是非交互的，可以在采集完成后開始學習，而強化學習的樣本是交互式的，需要在學習的同時生成新的樣本，邊采樣邊學習。在學習過程中，PPO設計了一個長度為的緩沖區，智能體與環境使用舊策略交互次，將交互過程生成的交互時間序列={,,,…，}存儲于緩沖區中。更新策略網絡時，首先使用式(33)估算(,)，然后根據高斯分布的概率密度函數計算中已執行行為的(|)。策略網絡生成新的策略后計算(|)，然后代入式(36)計算目標函數，使用ADAM優化器求得目標函數對的梯度并更新策略網絡，使目標函數最大化。

表1 策略網絡與評價網絡各層維度Table 1 Layer size of actor network and critic network

更新評價網絡時，目標函數中的優勢函數(,)在更新策略網絡階段已經獲得，可直接代入式(31)。使用ADAM優化器優化評價網絡的損失函數，更新評價網絡的參數，使損失函數最小化。兩個網絡更新完成后，清空緩沖區，然后使用學習后的新策略交互次，重復這一學習過程，直至導彈落地或擊中目標。

5 仿真實驗

為了測試LCG的性能，本節給出了三維空間的數值仿真實驗。首先建立了三維空間的導彈運動模型，然后使用DSLM分別學習了水平通道與垂直通道的飛行狀態與落角之間的關系，使用DRLM實現了兩個通道的落角控制，最后使用蒙特卡洛仿真驗證了LCG的有效性。

5.1 三維空間導彈運動模型

三維空間的導彈運動微分方程為

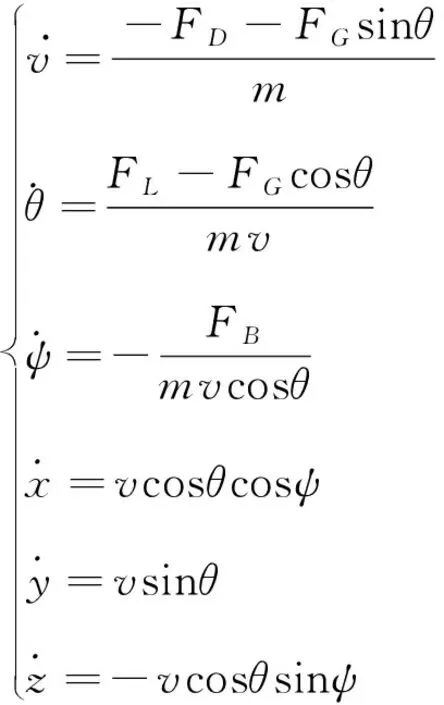
(42)

式中：為飛行速度；為彈道傾角；為彈道偏角；、、為導彈在空間中的位置；為導彈質量；表示升力；表示側向力；表示阻力；表示重力。各氣動力形式為

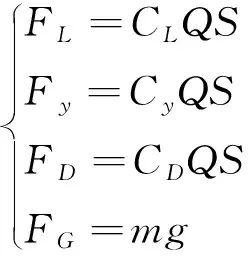
(43)

式中：為升力系數；為側向力系數；為阻力系數；為動壓；為參考面積。攻角和側滑角一般較小，氣動系數可近似表示為

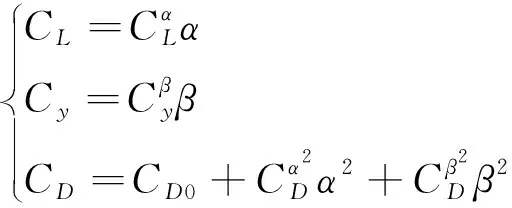
(44)

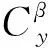
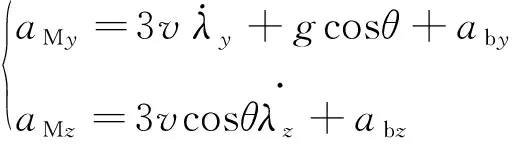
(45)

攻角、側滑角與制導指令之間M、M的關系如下

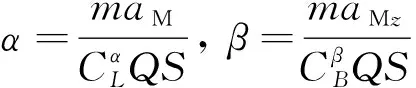
(46)

5.2 DSLM仿真實驗

在訓練DSLM之前，需要設計仿真飛行實驗，以PNG為制導律采集彈道樣本。本文設計的DSLM可以在水平通道和垂直通道獨立訓練，然后分別部署于兩個通道，因此分別了開展縱向平面和和側向平面的仿真實驗，并且訓練了兩個通道DSLM模塊。

導彈的初始飛行狀態以均勻分布的方式從一定范圍內隨機選取。各初始飛行狀態的取值范圍如表2所示，表3給出了導彈關于馬赫數的氣動系數，由于本文使用軸對稱彈體模型，導彈水平通道的氣動參數與垂直通道的氣動參數相等。導彈的參考面積=0057 m，質量=200 kg，重力加速度=981 m/s。攻角與側滑角均限制于區間[-20°,20°]內。其中縱向平面重復了兩組蒙特卡洛實驗，第1組實驗不考慮氣動系數攝動，通過1 000次仿真實驗獲得9 191 009組樣本；第2組實驗設定攝動參數，在每次實驗的初始化階段隨機縮放氣動系數，的取值范圍為(0.8,1.2)，運行1 000次仿真實驗共獲得10 207 724組樣本，首先使用無氣動系數攝動的樣本訓練DSLM，訓練結束后使用有氣動系數攝動的樣本繼續訓練DSLM；側向平面運行了一組蒙特卡洛實驗，使用攝動參數隨機縮放氣動參數，的取值范圍為(0.8,1.2), 運行1 000次仿真實驗共獲得21 339 882組樣本，使用該樣本訓練另一個DSLM，用于水平通道的落角預測。

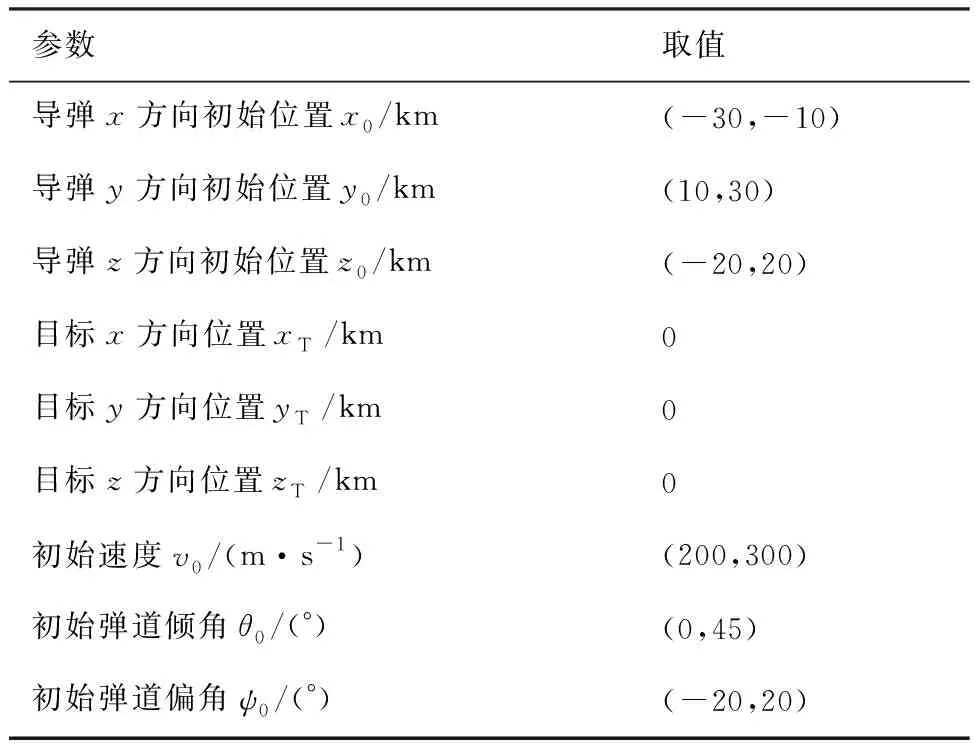
表2 導彈初始飛行狀態Table 2 Initial flight conditions of missile

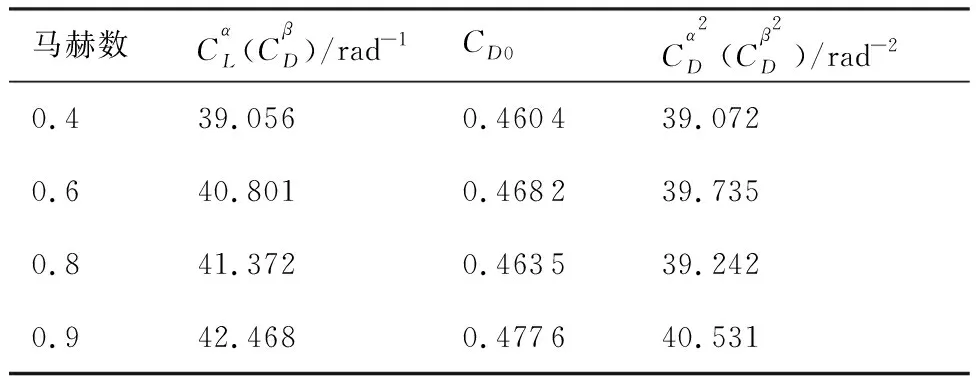
表3 氣動系數及導數Table 3 Aerodynamic coefficients and derivatives

使用測試樣本測試訓練好的兩個DSLM，測試結果如圖5所示，測試集的預測誤差統計特征如表4所示。由圖5可見DSLM對落角具有良好的預測效果，預測值與實際值幾乎完全重合，由表4可見預測誤差的均方根誤差較小，最大值雖然較大，但較大的誤差一般出現在彈道初段，預測誤差隨著導彈接近目標逐漸收斂。實驗結果證明了DSLM的輸入輸出選取合理，學習效果良好。

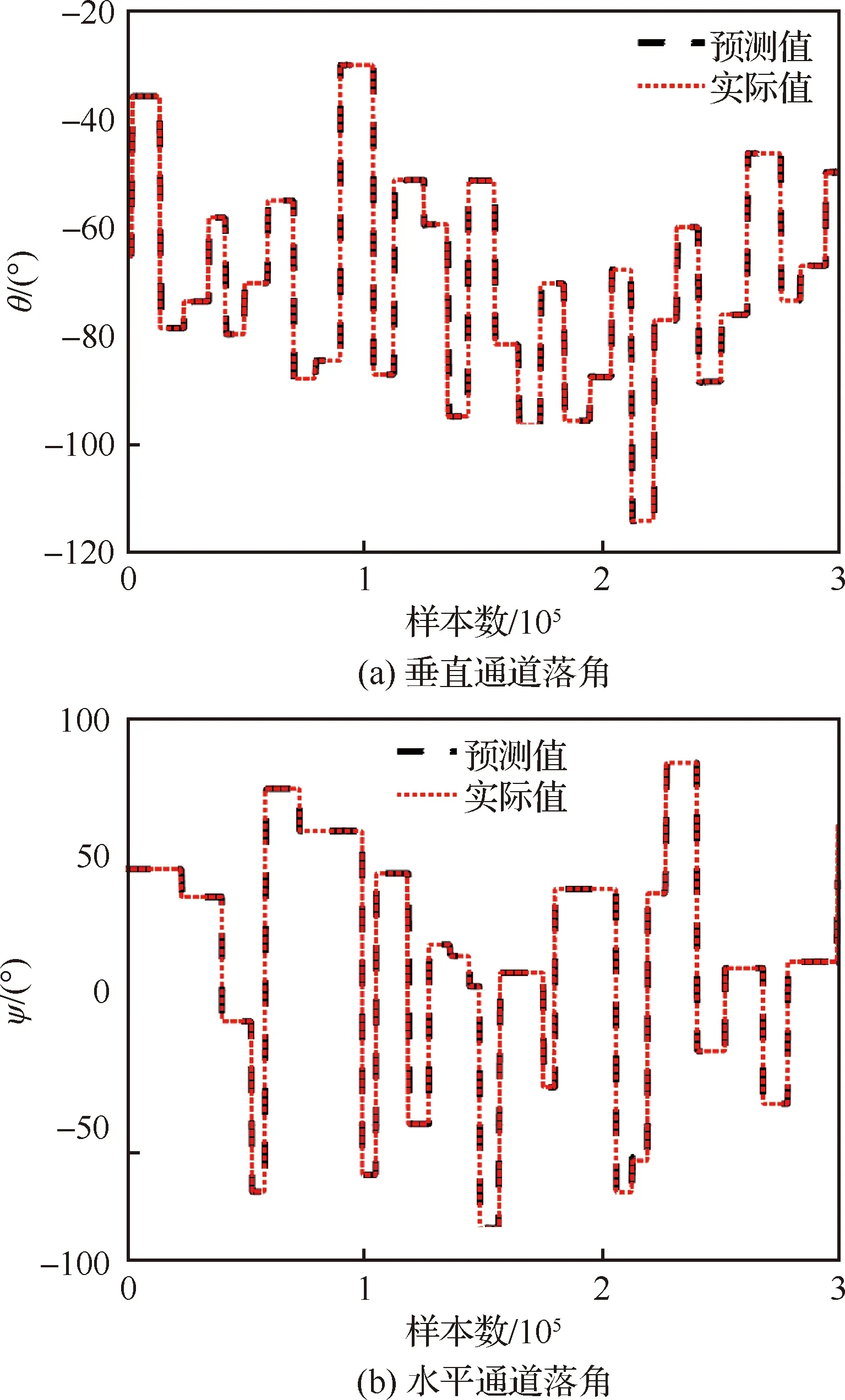
圖5 DSLM測試結果Fig.5 Test results of proposed DSLM predictor

表4 DSLM預測誤差的統計特征Table 4 Statistical characteristics of DSLM prediction error

5.3 DRLM仿真實驗

1) DRLM的學習過程

由于DRLM的輸出僅依賴落角預測誤差，而水平通道和垂直通道的氣動系數相近，可以使用相同的DRLM模型，因此僅在二維縱向平面訓練DRLM，然后將訓練好的DRLM部署于兩個通道。DRLM的樣本獲取方式與DSLM不同，采用了邊采樣邊學習的方式。根據4.1節設計的強化學習模型在導彈仿真飛行實驗中部署PPO算法，按照表2中給出的取值范圍隨機選取導彈的初始飛行狀態，在學習階段期望落角從[-30°,-150°]中隨機選取。PPO學習時使用的超參數如表5所示。式(15)和式(20)中的可以通過式(47)近似計算得出:

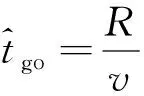
(47)

運行仿真程序500次，記錄每一次仿真飛行實試驗獎勵值，然后除以該次飛行時間，記為單次仿真飛行實驗的獎勵。使用滑窗平均計算多次飛行實驗的平均獎勵，獎勵隨學習過程收斂的曲線如圖6所示。從圖中可見，經歷了100個周期的波動后，獎勵值開始單調上升，并在第200次試驗后趨于穩定。

2) DRLM性能分析

設定一系列的場景對訓練后的LCG進行仿真測試，導彈以=200 m/s，=0°，=0°，=-20 km，=10 km，=5 km的初始狀態發射，期望彈道傾角和期望彈道偏角(,)分別設定為(-20°,20°)，(-40°,0°)，(-60°,-20°)，各飛行試驗對應的彈道曲線、制導指令、飛行速度、速度方向角如圖7所示。

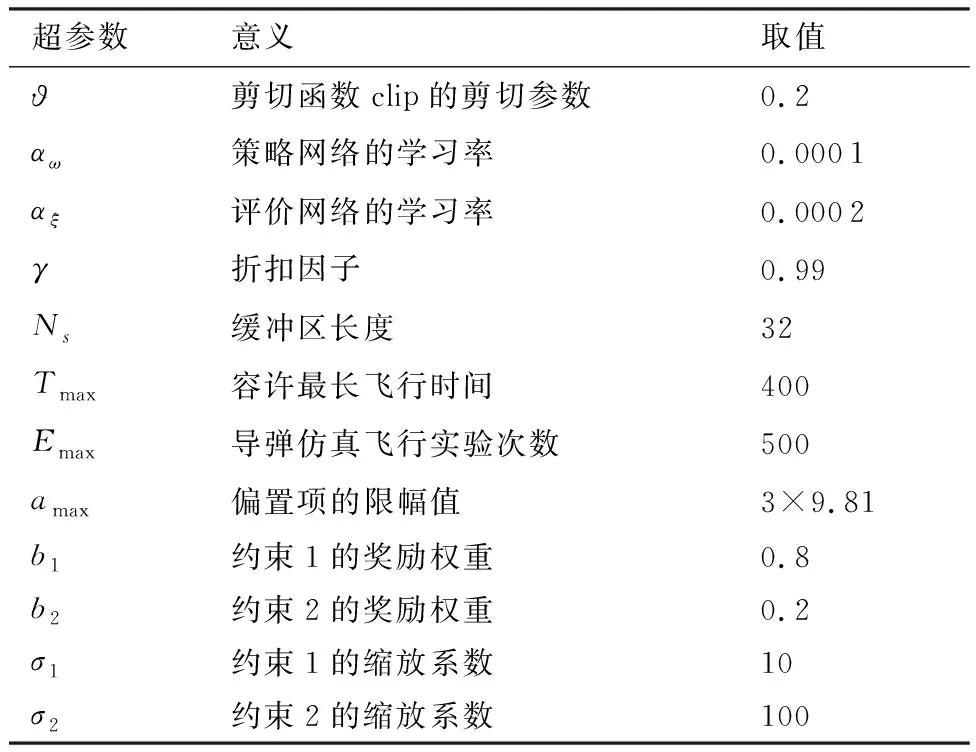
表5 DRLM的超參數Table 5 Hyper parameter setting in training DRLM

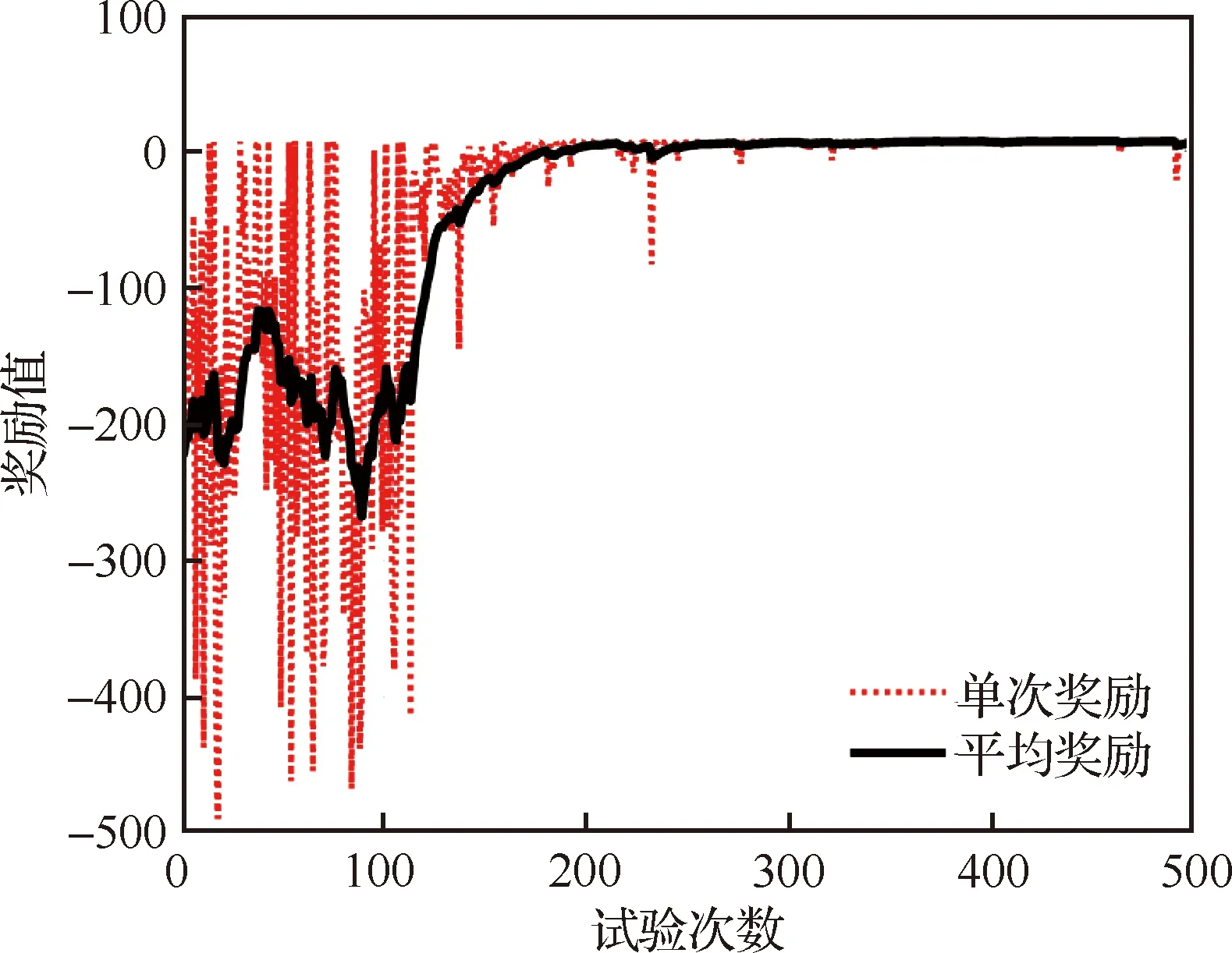
圖6 DRLM學習過程獎勵曲線Fig.6 Learning curves of the DRLM

從圖7中可見，導彈以期望的落角命中目標，制導指令有界。阻力與重力的聯合作用致使飛行速度變化，當-sin>時，飛行速度增大；反之，當-sin<時，飛行速度減小。導彈的和在仿真終端時刻為(-19.79°,19.86°)，(-40.09°, -0.39°)，(-59.92°,-19.99°)，驗證了LCG能夠以較高的精度實現三維落角約束。

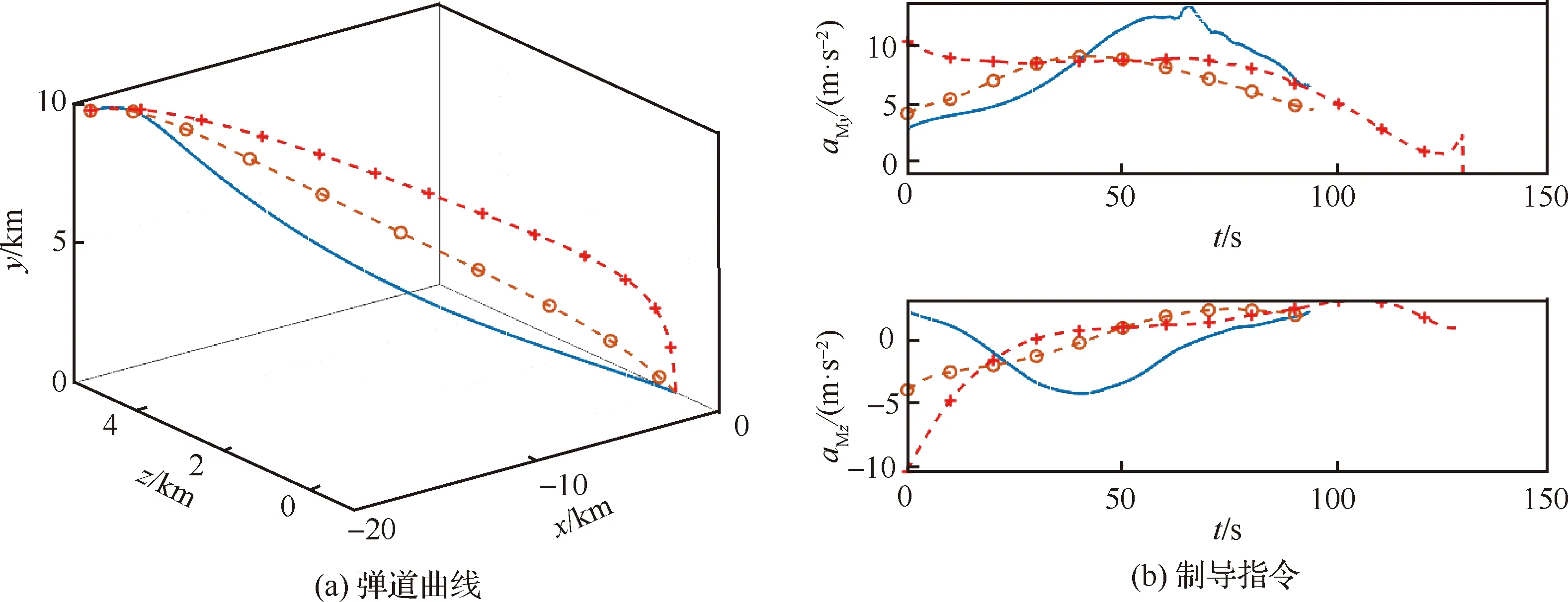
圖7 LCG制導性能曲線Fig.7 Performance curves of LCG

實際場景中一般存在模型偏差與環境擾動，導致氣動系數攝動。為了驗證LCG的魯棒性，在期望落角[,]為[-20°,20°]時，分別將表3的氣動系數放大1.2倍、縮小0.8倍，實驗結果如圖8所示。從圖8可見，在不同的氣動系數下導彈的飛行軌跡基本重合，并且均以期望的落角到達目標位置，且在到達目標時，落角誤差收斂至0附近。導彈的和在仿真終止時刻分別為(-19.28°,19.79°)，(-19.79°, 19.86°)，(-19.94°,19.91°)，驗證了基于預測校正制導思想設計的LCG能夠適應氣動系數攝動，具有較強的魯棒性。

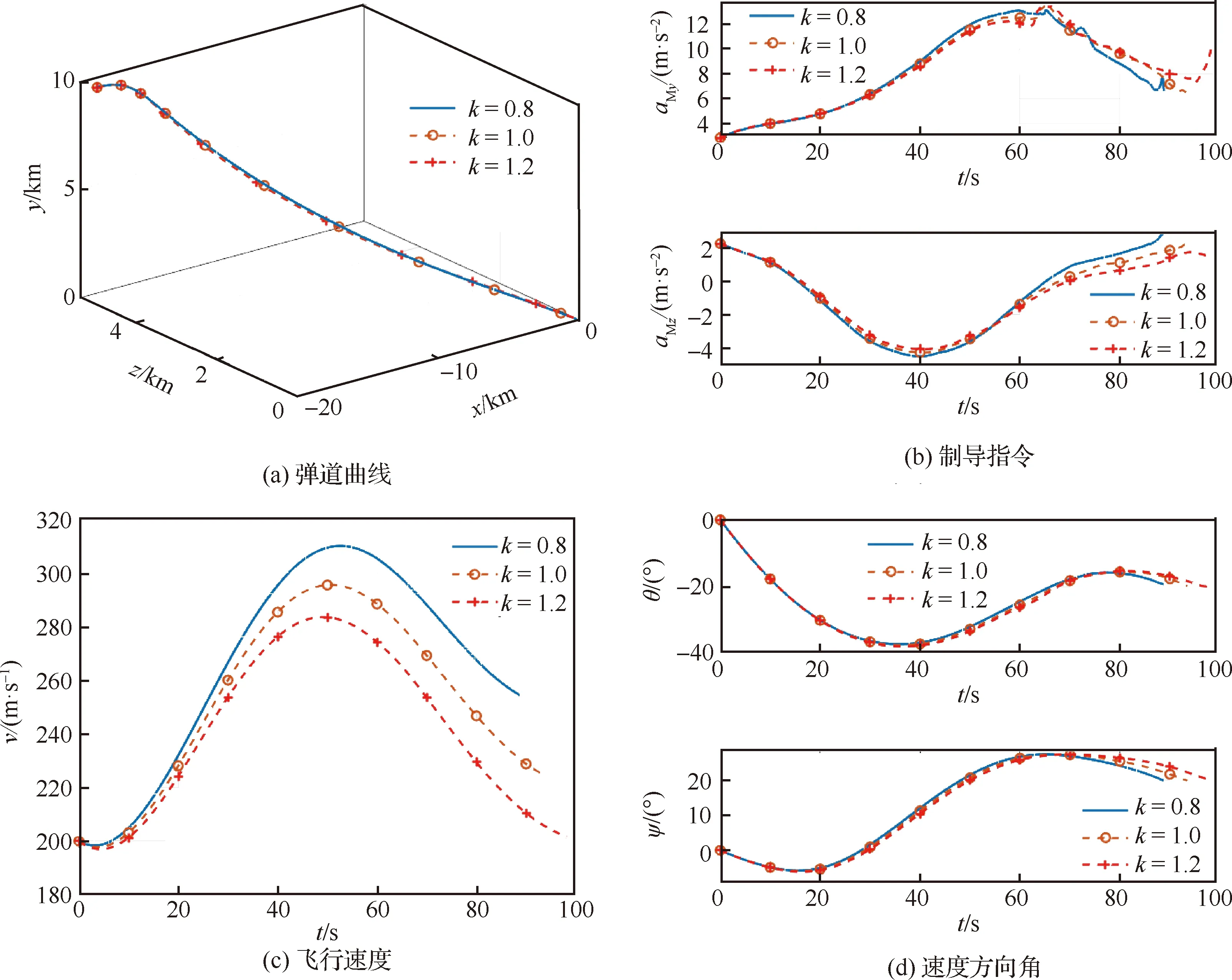
圖8 不同氣動系數下的LCG制導性能曲線Fig.8 Performance curves of LCG with different aerodynamic coefficients

3) LCG與彈道成型的對比分析

廣義最優彈道成型制導律(Trajectory Shaping Guidance, TSG)是一種帶落角約束的最優制導律，其推導過程引入了常值速度假設，沒有考慮氣動力的影響，在上述假設條件下TSG滿足能量最優的性能指標。三維場景中TSG的公式為

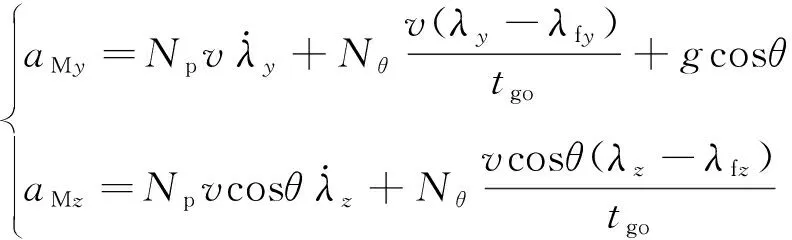
(48)

式中：、為導航系數；f、f為終端彈目視線角；對固定目標有f=f、f=f。各導航系數形式為

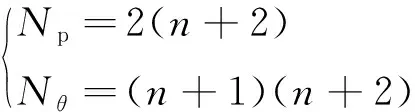
(49)

式中：為可調參數，≥0。

取與2)相同的初始發射條件，設期望落角(,)為(-40°,0°)，分別設定=0,1,2，運行仿真實驗對比3組不同參數的TSG與LCG的制導效果，實驗結果如圖9所示。兩種制導律均使導彈以期望的落角到達目標位置，雖然在=0時TSG為能量最優的落角約束制導律，但是TSG的推導過程沒有考慮氣動力的影響，使用了常值速度假設，在實際環境中無法滿足能量最優。而LCG在訓練階段考慮了氣動力的影響，DRLM通過試錯交互學習得到了滿足落角約束的制導策略，并且能量消耗優于TSG，說明本文的DRLM的獎勵設計合理，在實際環境中LCG的制導性能優于TSG。

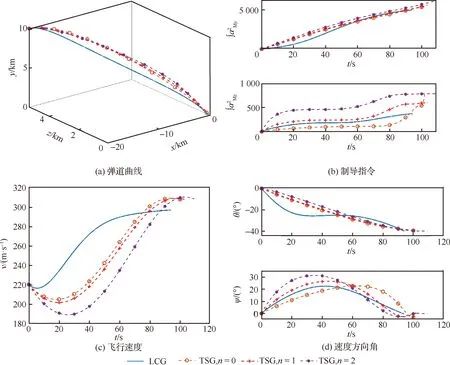
圖9 LCG與TSG性能對比Fig.9 Performance comparison of LCG with TSG

5.4 蒙特卡洛實驗

為了測試LCG在不同狀況下的制導性能，使用蒙特卡洛仿真實驗，發射條件從表2給出的范圍中隨機選取，期望落角(,)分別從(-60°,-20°)、(20°,20°)中隨機選取。分別以LCG與=0的TSG為制導律重復100次蒙特卡洛實驗，統計LCG與TSG的落角誤差，統計特征與箱線圖如表6、表7和圖10所示，圖中、分別表示垂直通道和水平通道的落角誤差。從箱線圖可知，LCG落角誤差的方差、異常值均小于TSG，驗證了該方法對環境變化不敏感，具有較強的抗擾性、魯棒性；LCG脫靶量的上限、上四分位數、中位數均小于TSG，驗證了LCG能夠按照要求完成制導任務，制導性能優于TSG。

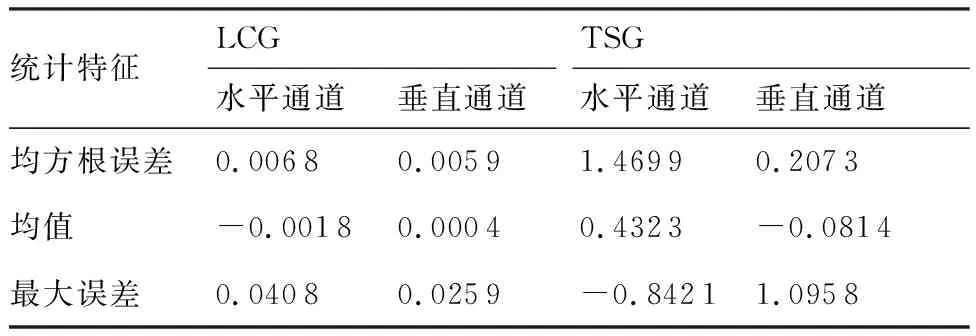
表6 落角誤差的統計特征Table 6 Statistical characteristics of impact angle error

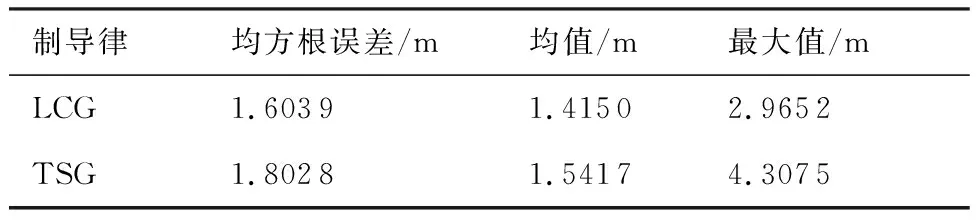
表7 脫靶量的統計特征Table 7 Statistical characteristics of miss distance

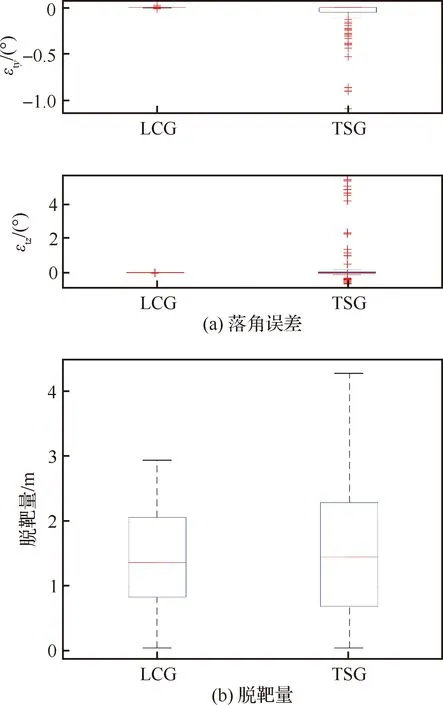
圖10 蒙特卡洛仿真實驗結果對比箱線圖Fig.10 Box plot of Monte Carlo experiment

5.5 計算性能實驗

與傳統的制導律相比，計算制導方法需要消耗更多的計算資源。為了驗證本文提出的LCG在嵌入式系統的工程實用性，依次使用TensorFlow 1.13.1、X-CUBE-AI 6.0.0、STM32CubeMX 6.2.1分別將LCG中的預測網絡、策略網絡部署于STM32F405測試平臺，其中X-CUBE-AI是ST公司開發的AI工具箱，可以優化神經網絡在STM32上的運算速度。分別部署DSLM的預測網絡和DRLM中的策略網絡，實驗流程如圖11所示。

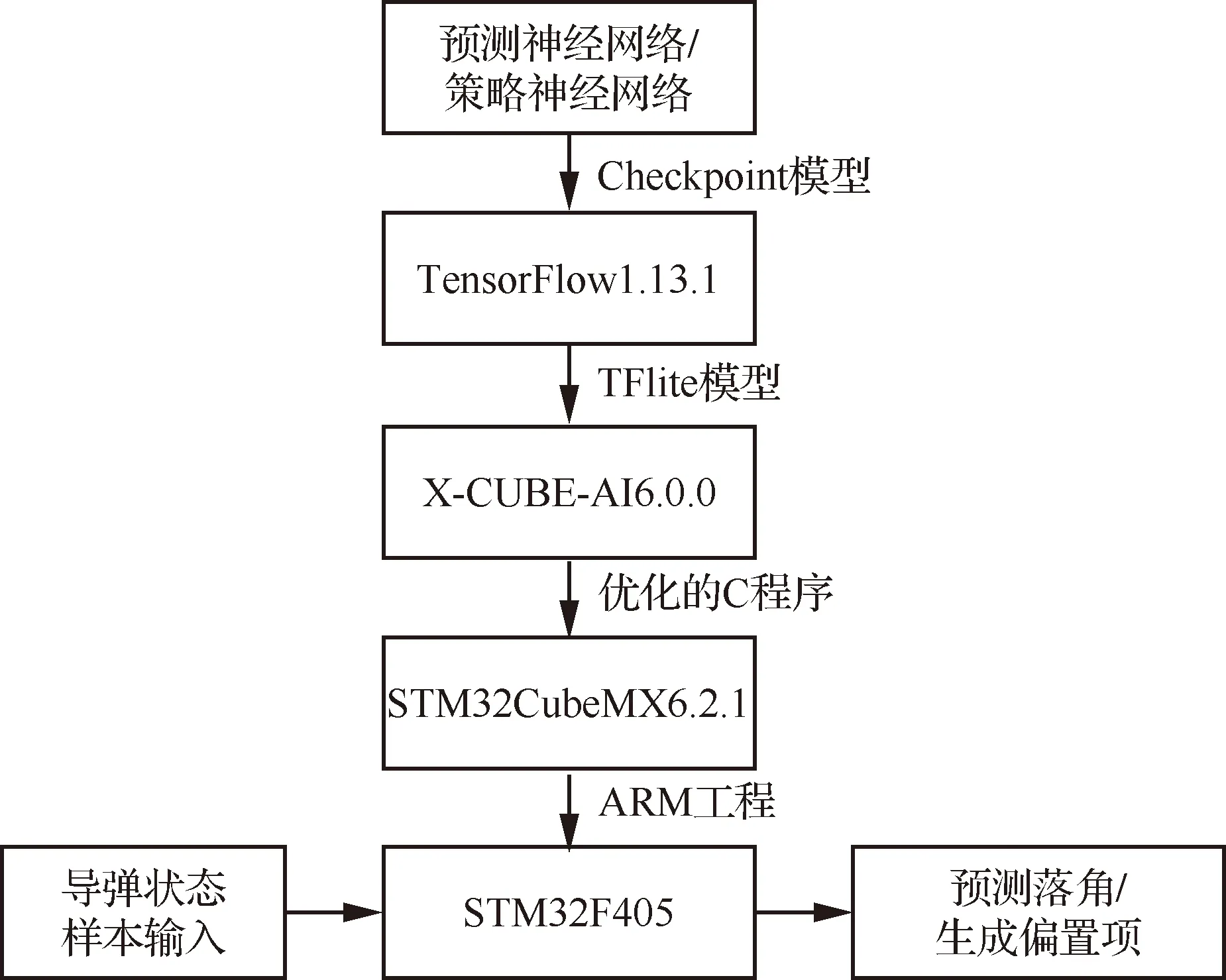
圖11 STM32F405實驗流程示意圖Fig.11 Experimental flow diagram of STM32F405

PC通過串口下發數據，使兩組神經網絡各運行10次，然后通過串口采集神經網絡的輸出值，并統計神經網絡運行耗時。將STM32F405的輸出值與PC平臺的神經網絡輸出值進行對比，測試X-CUBE-AI優化神經網絡造成的精度損失，并計算平均耗時，結果如表8所示。

表8 STM32F405運算精度與耗時Table 8 Precision and time consumption of STM32F405

從表8可見，兩組網絡在STM32F405單次運行的平均耗時分別為1.145 ms和0.272 ms，計算精度高，實時性好，說明LCG具備工程實用價值。

6 結 論

1) 提出了一種基于預測校正的落角約束計算制導方法，該方法由深度監督學習模塊與深度強化學習模塊組成，深度監督學習模塊在飛行過程中實時預測落角，深度強化學習模塊對落角誤差進行校正。引入深度監督學習網絡解決了傳統強化學習方法中的稀疏獎勵問題。

2) 設計了計算制導方法中的各輸入輸出變量，經訓練后實現了落角約束制導，并以仿真實驗的形式測試了計算制導的性能，該算法訓練過程的收斂速度較快，訓練后的制導效果較好，能量消耗與控制誤差均小于彈道成型制導律。然而，由于該類算法較依賴訓練時所使用仿真模型的準確度，當訓練模型存在較大偏差時，將影響本文所提出方法的制導性能，后續將開展基于數據的計算制導方法的魯棒性研究，探索弱監督學習、遷移學習在當前計算制導框架的應用。

3) 經STM32F405測試，該框架計算精度與效率高，實時性好，具有良好的工程應用價值。該框架對預測校正制導思想的使用除落角約束以外，也可以應用于其它不同約束，如飛行時間約束、末速約束等。