數理統計課程中Cranmer-Rao不等式的教學案例設計

陶 紅，徐耀坤，何章鳴，侯臣平

（國防科技大學 a.文理學院；b.電子科學學院，湖南 長沙 410073）

引言

數理統計是統計學的一個重要分支，在自然科學、工程技術、管理科學和人文社會科學等領域得到了越來越廣泛的應用。很多高校的本科和研究生數學類與統計類專業均開設數理統計類課程。傳統的數理統計教學著重于定義與公式的講解與證明，這種講授方法雖然能夠準確傳達課程知識，但在激發學生學習興趣、培養數理統計思想、提升科研創新能力這些方面存在明顯的不足。為了提升學生的學習興趣，很多高校都在嘗試采用案例教學法來提升數理統計課程的教學質量。已有的教學實踐表明，在數理統計課程中引入案例教學模式，能夠有效幫助學生加深對理論知識的理解和提升解決實際問題的能力。案例教學法的推廣需要豐富的案例資源作為支撐。然而，目前我國高校數理統計課程的案例教學中，案例資源還比較匱乏。大多數案例內容陳舊，與當前社會的發展態勢聯系不夠緊密，從而限制了案例教學法的作用。由此可見，數理統計教學案例建設的必要性與緊迫性。本文針對數理統計課程中Cramer-Rao不等式的教學目標和教學重點，結合相關領域前沿研究成果，從單分子定位超分辨成像和鋰電池荷電狀態估計兩個實際應用中，凝練了兩個Cramer-Rao不等式的教學案例，加強課程內容與實際問題的有效結合。

一、Cramer-Rao不等式的基本理論

在案例教學開始，首先對案例涉及的基本概念進行詳細剖析。Cramer-Rao不等式的內涵是：對于Cramer-Rao正則族的可估參數，其無偏估計的協方差陣存在下界。這個下界被稱為Cramer-Rao下界，由樣本容量、Fisher信息和可估參數的導數確定。Cramer-Rao不等式的應用十分廣泛，可應用于雷達運動目標檢測、衛星定位系統、超精密測量和量子成像等科學研究和工程實踐中的參數估計精度分析，對于提升實際應用中的參數估計性能具有重要作用。由于Cramer-Rao不等式在理論研究和工程實踐中的重要地位，Cramer-Rao不等式一直是數理統計課程中的教學重點。

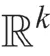
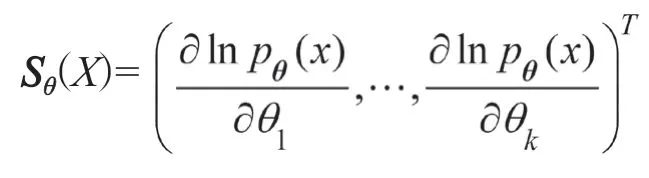
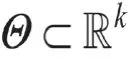
現有教材通常直接給出Fisher信息的定義與存在條件，然后再給出Cramer-Rao不等式的具體內容與證明。教師在教學的時候如果僅僅局限于教材，不結合實際應用進行適當延伸與拓展，那么學生對此部分內容的學習將停留于“背公式”的層面，不能深入理解Cramer-Rao不等式的應用途徑。因此，需要發揮數理統計作為一門應用性極強的學科的特點，積極進行案例建設，擴大案例式教學法在數理統計教學中的應用范圍，從而提升教學質量。事實上，Cramer-Rao不等式作為參數估計中誤差分析的有力工具，已經在相關學科中得到廣泛應用，結合基本理論，讓我們分析以下案例。

二、Cramer-Rao不等式的案例設計

實際的教學案例設計中，要考慮學生對案例背后知識背景的掌握程度。筆者結合學生的已學課程，通過查閱相關學科的前沿研究成果，分別從單分子定位超分辨成像和鋰電池荷電狀態估計兩個實際應用中凝練了兩個Cramer-Rao不等式的教學案例，學習過“大學物理”基本課程的學生均可理解案例中的基本背景。兩個不同的案例中，既有諾貝爾獎工作中的科學問題，又有貼近實際生活的工程問題，現予以分享。

案例1 基于單分子定位的顯微成像技術（Single-Molecule Localization Microscopy,SMLM）獲得2014年獲得諾貝爾化學獎。SMLM的工作原理可以概括為“閃爍”“定位”與“重建”，即多次循環采集被稀疏激活的熒光分子，再利用單分子定位算法給出熒光分子精準的空間定位信息，最后將每一幀的定位點合成為一張超分辨圖像。單分子定位算法的精度分析是成像分辨率分析中的一個基本且重要的問題。事實上，單分子定位就是對單分子的坐標進行估計。若獲得了單分子坐標的無偏估計量，則此估計量的定位精度定義為其標準差。

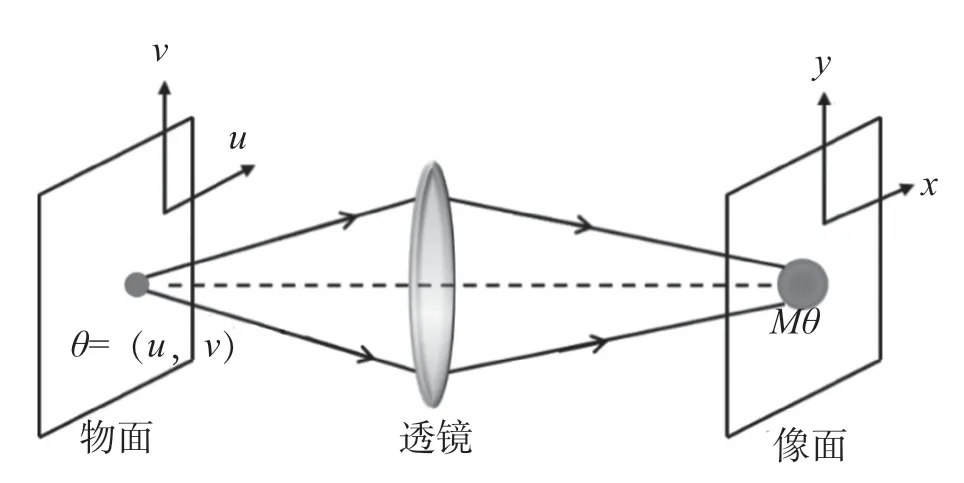
圖1 單分子成像系統

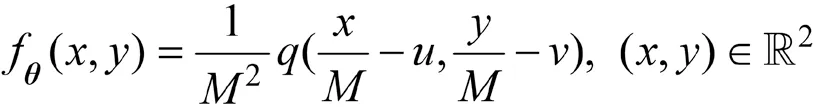
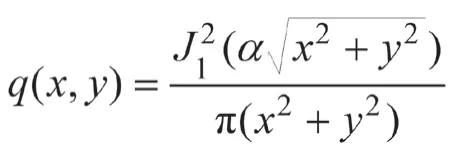
若采集到個光子，由此個光子的坐標構造出的的模平方可積的無偏估計為，且已知

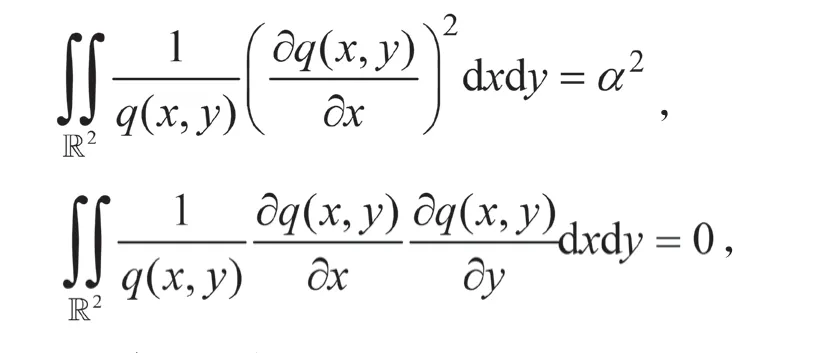
試求的方差下界。

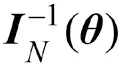
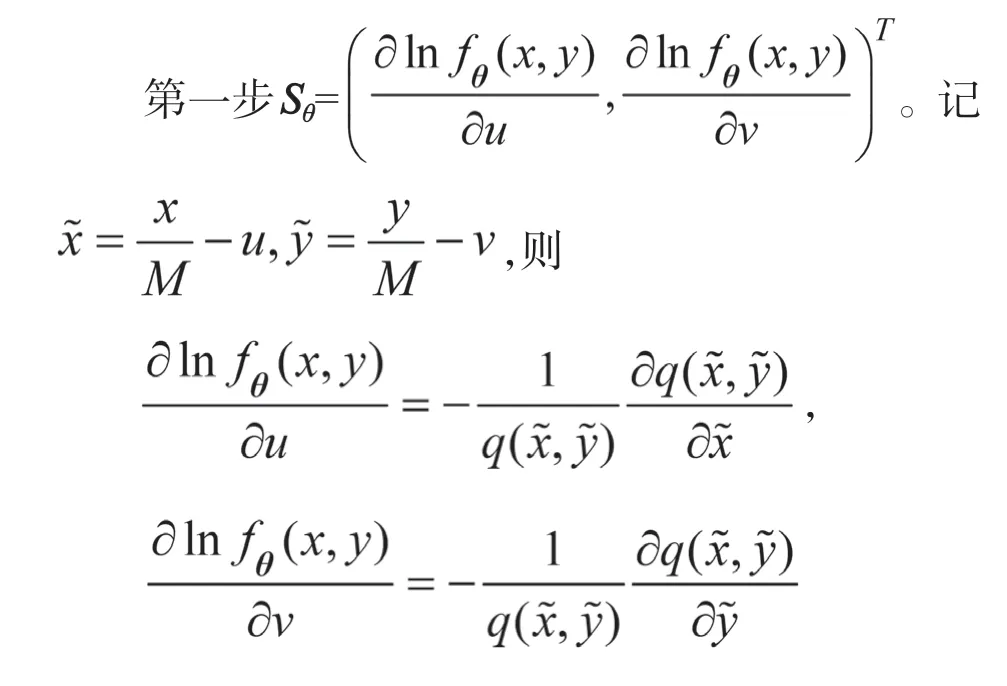
第二步，計算（）。

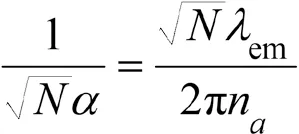
案例2 鋰電池因其能量密度高、循環壽命長等優點迅速發展為新一代儲能電源。準確估計電池當前工作狀態，對于提高儲能系統的安全性、可靠性和可用性具有重要作用。假設鋰電池內部具有圖2所示的RC等效電路模型。

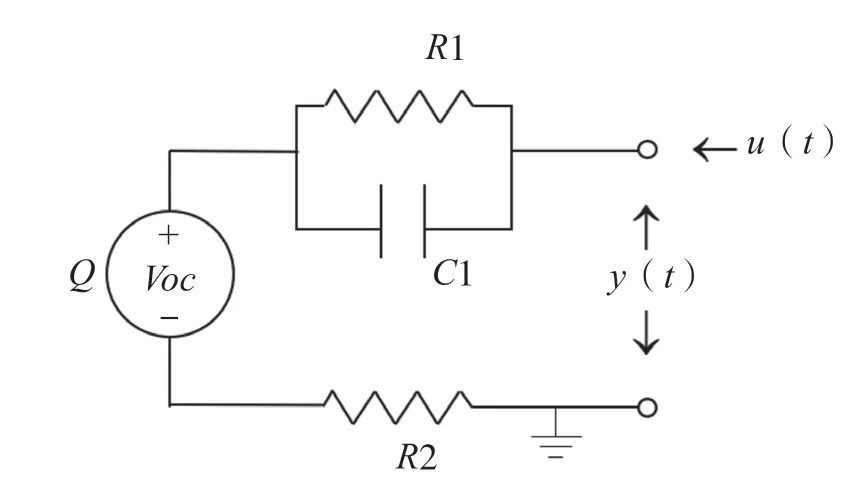
圖2 鋰電池內部RC等效電路圖

此等效電路的工作原理為

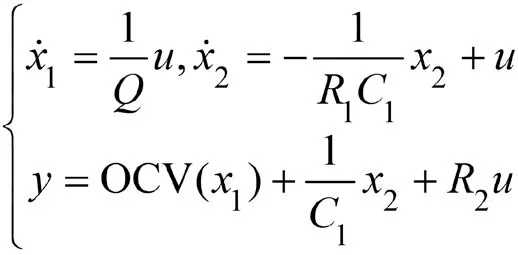
其中表示電池的荷電狀態（SOC），和分別表示電池的極化內阻和極化電容，表示平行電容器的電荷量，表示電池電量，表示電池歐姆內阻，表示輸入電流，表示可直接測量的電池端口電壓，OCV（）表示開路電壓與SOC間的非線性關系并且可以通過實驗測量得到。

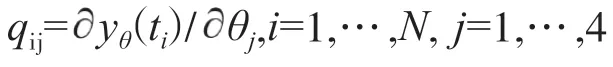
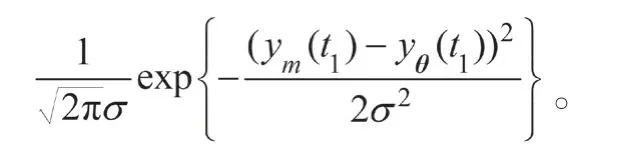
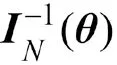
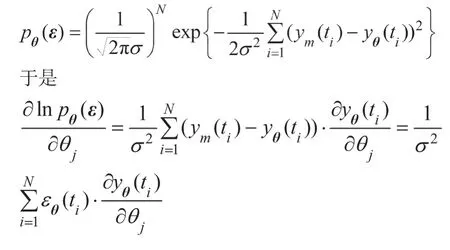
則根據Fisher信息的定義知

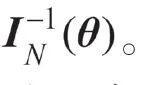
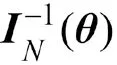
在此次教學案例設計中，我們選取了兩個不同領域的例子，用來幫助學生理解不等式的深刻含義。通過以上兩個案例的分析，讓學生對枯燥的理論公式有了直觀的理解和認識，讓他們感受到Cramer-Rao不等式在科學研究和工程實踐中的應用。上述兩個案例雖然看上去計算量比較大，但是根據Cramer-Rao不等式的內容及Fisher信息的定義，均能很快得到無偏估計的Cramer-Rao下界。上述案例雖然來自不同的研究領域，但是其中涉及的參數估計的精度分析屬于同一類型的統計問題。在案例運用時，一方面結合背景開闊學生視野，另一方面重點讓學生領會統計原理、掌握統計方法，對于計算量可以根據情況進一步簡化。案例2相比于案例1，拓展了試驗設計的相關內容，能夠讓學生更加直觀地感受Cramer-Rao不等式在實踐中的重要作用，并在此過程中學會運用Cramer-Rao不等式。結合以上兩個案例，可以在教學過程中通過討論互動的方法，讓學生總結利用Cramer-Rao不等式解決具體問題的方法和步驟，更加深入地理Cramer-Rao不等式的基本理論，從而更好地發揮案例教學法的作用。

三、結語

Cramer-Rao不等式在數理統計中具有重要地位。雖然Cramer-Rao不等式的教學內容便于理解，但是學生對于Cramer-Rao不等式在實際應用中能夠解決什么問題、怎樣解決問題缺乏直觀認識。本文針對Cramer-Rao不等式案例資料有限的情況，查閱相關領域的前沿研究成果整理出兩個案例，希望通過案例展示幫助學生將Cramer-Rao不等式的理論與實踐緊密結合起來，鍛煉學生發現問題、分析問題和解決問題的能力。