結構化教學讓復習課增效

◇汪靜靜（江蘇：淮安市淮海小學）

復習是小學教學的重要環節，具有鞏固知識、查漏補缺、形成技能、發展思維、診斷教學等功能，在學生的數學學習中有著至關重要的作用。反觀日常的教學實踐發現，部分教師對復習課的重要性認識不足，復習教學中存在形式固化、重復低效、題海戰術、教師主導等問題，缺少趣味性、挑戰性、綜合性和整體性，學生則是索然無味、機械刷題、缺乏主動性，復習效果欠佳。2022 版新課標指出：在教學中要重視對教學內容的整體分析，幫助學生建立能夠體現數學本質、對未來學習具有支撐意義的結構化的數學知識體系。教師要有“整體意識”，基于結構化視角設計復習課，關注知識之間的邏輯性、系統性和關聯性，引導學生自主整理所學知識，使之形成結構化的知識網絡，有效提升復習效能，促進學生全面發展。下面以蘇教版六下“平面圖形的周長與面積總復習”為例，談談自己的探索與思考。

一、重建師生關系，凸顯育人價值

鐘啟泉教授認為：“課堂教學應以學生的自主活動為中心展開。所有的構成要素都應當為形成學生的自主活動而加以統整，都必須服從于學生自主活動的組織。”復習課上，要改變“重知識傳授，輕能力培養”“重碎片學習，輕整體架構”“重教師主導，輕學生自主”等現狀，注重學生的學力培養和知識結構的建構。要建立和諧的師生關系，尊重學生的個體差異，營造輕松、融洽、包容性強的學習氛圍，允許學生犯錯、重講、補充或求助，使學生在課堂上不拘謹、不害怕，能夠大膽地展示自己，主動投入學習中。

（一）重心下移，以生為本

例如本課教學中，教師多次組織學生獨立思考、同伴互助、小組交流，讓學生走上講臺當小教師，介紹長度單位、面積單位的相關知識；充分利用EN5 的互動操作功能，在白板上邊操作邊講解各平面圖形面積公式的推導過程。學生在選擇、復制、旋轉、移動、講解等操作活動中興趣盎然、積極主動，他們動了起來、活了起來，獲得滿滿的成就感，鍛煉了膽量，培養了數學思維和語言表達能力。

（二）找準站位，適時引導

課堂上，教師要“心中有人”“目中有生”，學會找準站位、適時引導、及時退位，基于學生視角開展教學。如本課教學中，無論是課前自主整理形成各具特色的知識圖、課上學生走上講臺展示交流，還是課末欣賞學生用平面圖形設計出的創意畫、對學生收集的錯題進行分析分享……都能使學生的思維過程可視化，促進了學生數學思維的深度發展，凸顯了數學學科的育人價值。

二、經歷梳理過程，建立知識體系

結構化教學更關注“授人以漁”，方法比結果更重要。對某一階段或某一領域所學的知識進行歸納整理，是復習課順利進行的前提。教師應有“學生本位”意識，放手讓學生經歷知識的梳理、整合、分析、積累的過程，構建科學的知識體系，使之條理化、系統化、網絡化。

（一）整體把握，自主整理

小學中高年級學生已經具備相應的整理知識、回顧反思的意識與能力。因此，復習設計時教師可將整理“平面圖形周長與面積的相關知識”這一學習任務調整至課前，放手讓學生對這部分內容進行自主性的歸納整理。學生調用已有的學習經驗，呈現出了不同層次的梳理形式，如文字表述式、圖文并茂式、條目式、思維導圖式……

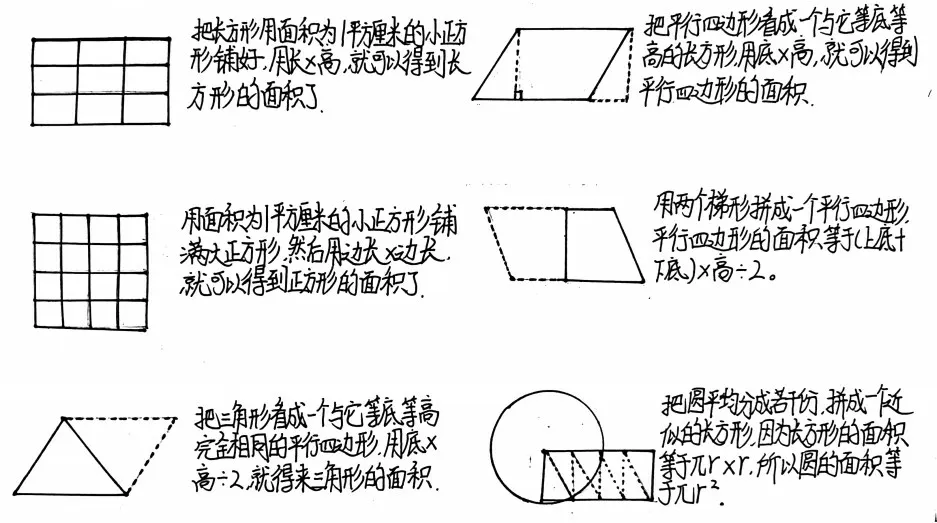
應將更多的課堂時間與空間留給學生，讓他們交流、互學、啟迪、完善、提升。通過教師的引導，學生掌握了一些基本的整理方法，養成回顧、整理、反思的好習慣，會對他們的繼續學習終身有益。

（二）串珠成鏈，織網成面

數學學科知識不是各個知識點的簡單累積和堆砌，而是一個有機整體。因此，教師在教學中要幫助學生尋找零散、細碎的知識之間的內在聯系，并將其串聯起來，“豎成線、橫成片”，形成由點、線、面架構起的“立體式”的整體知識網絡。

復習本課時，通過回顧所學知識，可以發現與平面圖形的周長與面積相關的知識點多而碎，如：什么是平面圖形的周長？什么是平面圖形的面積？如何求平面圖形的周長與面積？周長與面積的計算公式是怎么推導出來的？……這些知識點猶如一顆顆晶瑩的珍珠散落在各個年級、各個角落。如果帶領學生按部就班地一問一答，采取扁平化、條目式的復習方式，課堂復習時間肯定不足，學生也將興味索然，復習效果可想而知。

復習中，教師改變“乒乓球式”的問答方式，拋出一個大問題：“關于平面圖形的周長與面積，你是怎么理解的？”學生通過畫一畫、指一指、描一描、摸一摸、說一說等活動認識到：雖然長方形、正方形、三角形、平行四邊形、梯形、圓形、不規則圖形的周長與面積在外表形態上各不相同，但其本質是一致的，即“封閉圖形的周長是它所有邊的長度之和，封閉圖形的面積是指它的面的大小”。在大問題的引領下，學生有效地將一些零散的知識點串編成一條美麗的“項鏈”，有利于幫助其形成一個具有生命力的思維網絡，從而使他們深刻體會到概念的本質屬性，掌握蘊含在概念關系中的各種思維模式。

（三）多維勾連，融會貫通

俄國教育家烏申斯基說過，智慧是一種組織得很好的知識體系。碎片化的、孤立的知識是沒有價值的，而知識的整體化就是針對知識的碎片化而言的，強調知識的結構化、整合化，防止知識的孤立化、片面化，是將知識轉化為核心素養的基本要求。

本課教學中，在師生討論交流、互助互學、完善提升的基礎上形成了較為完整的知識結構圖。但教師這時并沒有就此結束復習，而是引導學生從不同角度進行分析與觀察，促使學生進行深度學習與思考：

這些公式的推導過程之間有什么聯系嗎？你能用箭頭連一連嗎？

你是怎么理解平面圖形面積公式推導過程之間的聯系的呢？

從左往右，你發現了什么？從右往左看呢？

旋轉知識結構圖，引導學生換個角度觀察：你發現了什么？學生驚喜地發現這幅圖像一棵知識“樹”，能夠很好地體現圖形與圖形之間的內在聯系，而且長方形的面積計算公式還是其他平面圖形面積公式推導的基礎，是“樹根”。

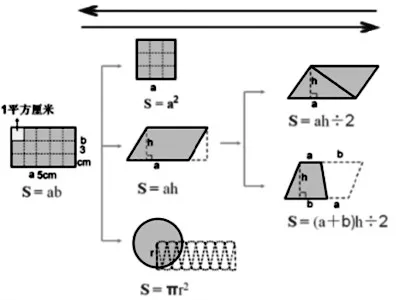
此環節的設計不僅注重了知識體系的建構、數學思維的提升，還關注了數學思想、數學文化的滲透。比如在整理出平面圖形面積推導過程的知識圖后，分別引導學生“從左往右”和“從右往左”進行觀察與思考，說說自己的發現：由已學的圖形面積計算公式可以推導出新圖形的面積計算公式，在推導一種新圖形面積計算公式時可以把它轉化成已學過的圖形來解決。“轉化思想”的滲透使本節課的復習有了一個“由薄到厚”和“由厚到薄”的過程。在此過程中學生的語言表達、數學思考、觀察分析、歸納總結等能力得到了切實的培養與提升。

三、創編多元練習，構建數學模型

數學模型是建立在數學基礎知識與數學實踐應用之間的紐帶，通過不同形式的鞏固練習可以促進學生有效建模，而建模更為重要的是用現實的情境表述數學問題，幫助學生在解決實際問題的過程中內化知識、加深理解。實際教學中可以設計形式多樣的習題，如知識類習題、趣味性習題、實踐類習題、整合類習題、跨學科融合習題等。本課教學中，習題選擇具有基礎性、實踐性、融合性和綜合性，做到了少、精、活。例如觀察學校操場平面圖，根據相關信息提出數學問題并解答：自主編題并判斷是解決什么問題的？如給汽車車窗裝上玻璃，需要多大的玻璃？給玻璃的四周安上封條，需要多長的封條？給一張圓形飯桌配上桌布，至少需要多大的桌布？繞著湖邊跑步一圈，跑了多少米？通過錯題分享、優題推薦、難題探討，挑戰自我。

學生在題組練習、對比練習、辨析交流、錯題分享中深化理解這部分知識，不僅明確周長與面積是兩個不同的概念，即兩個圖形周長相等，但面積不一定相等；面積相等，周長卻不一定相等，而且深刻感悟“轉化”這一數學思想的應用價值，主動構建模型。

四、延展學習時空，提升綜合素養

拓展延伸是一節課的延續與補充，是對本節課所學內容的延展，是培養學生思維能力、創新能力、實踐能力的關鍵環節。內容上，可以從書本延伸到課外；空間上，可以從課堂延伸到生活；學科上，可以從數學這一單科學習延伸到與其他學科的相互融合等。本節課引導學生進行全課總結時，并不僅僅停留在知識層面上，而是通過平面圖形的運動與變化所形成的各種立體圖形刺激學生的多方面感官，調動了學生進一步研究立體圖形相關知識的內驅力，使之很好地將學習熱情延伸到課外，延伸到更廣闊的領域中。

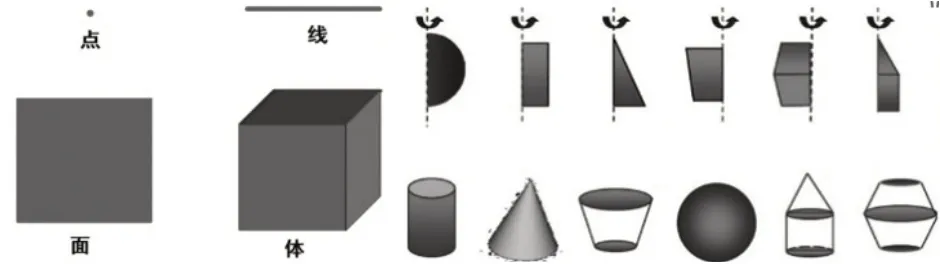
總之，教師要通過結構化的復習課教學，幫助學生對已學知識進行系統建構，形成條理化、網絡化的知識體系，實現1+1>2的效果。還要對學生的思維發展、能力提升起到一定的助推作用，有效提高數學復習課的“效能”；幫助學生建立起完整的知識結構和認知結構，使學生的學習更主動、更深入、更有效，促進學生綜合素養的全面提升，從而實現與學生共生長。