借助韋恩圖直觀理解事件的獨立性

程明春

重慶市江津中學校 402260

在概率的學習中，如何判斷和理解事件的獨立性是一個難點.部分情況可以憑直覺去判斷［1］，大多數(shù)時候則需要用概率關系去判斷.但因為概率關系較抽象，使得學生對事件獨立性的理解不夠深刻，甚至出現(xiàn)了錯誤.本文借助韋恩圖，讓事件獨立性直觀地呈現(xiàn)出來，并借此去分析互斥事件與對立事件的關系，以及相互獨立與兩兩獨立的區(qū)別.

相互獨立事件

定義［2］：對任意兩個事件A與B，如果P（AB）=P（A）P（B）成立，則稱事件A與事件B相互獨立，簡稱為獨立.

反之，若事件A與B獨立，即事件A發(fā)生與否不影響事件B發(fā)生的概率，我們將事件A發(fā)生的情況下事件B發(fā)生的概率記為，且設P（A）＞0，則P（B）=，即P（AB）=P（A）P（B）.

所以事件A與B相互獨立?P（AB）=P（A）P（B）.

相互獨立事件與互斥事件的關系

命題1：對于事件A與B，若P（A）＞0，P（B）＞0，則有：（1）若A與B獨立，則A與B不互斥；（2）若A與B互斥，則A與B不獨立.

證明：（1）若事件A 與B 獨立，則P（AB）=P（A）P（B）＞0，故AB≠，所以A與B不互斥；（2）若A與B互斥，則AB=，所以P（AB）=0，又P（A）P（B）＞0，所以P（AB）≠P（A）P（B），即A與B不獨立.

下面我們思考：如果事件A與B不互斥，那么A與B獨立嗎?

如圖1所示，在韋恩圖中，用SΩ，SA，SB，SAB分別表示事件Ω，A，B，AB的面積，于是可以用面積比來表示對應事件的概率.若Ω滿足古典概型，則可以用樣本點數(shù)量nΩ，nA，nB，nAB代替對應的面積.

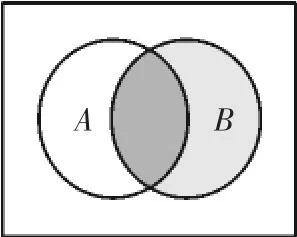
圖1

命題2：當P（A）＞0且P（B）＞0時，A與B獨立，等價于A與B不互斥，且在樣本空間Ω中事件A發(fā)生的概率與樣本空間B中事件AB發(fā)生的概率相等，即

對立事件的兩個易錯點

1.將互斥事件理解為獨立事件

例1一個袋子中有標號為1，2，3，4的四個球，除標號外沒有其他差異.從中摸取一個球，設事件A=“摸到1號球”，B=“摸到2號球”.試分析A與B是否獨立.

解析：容易錯誤地認為，在韋恩圖（圖2）中，表示事件A與事件B的區(qū)域不相交，故覺得它們是獨立的.錯因在于：A與B在韋恩圖中不相交，描述的是在一次試驗中A與B不能同時發(fā)生，即A與B是互斥關系；而A與B獨立，描述的是A的發(fā)生與否不影響B(tài)發(fā)生的概率.在該例中，若A發(fā)生，則B必然不發(fā)生，即A的發(fā)生會影響B(tài)發(fā)生的概率，所以A與B不獨立.

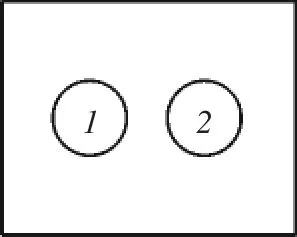
圖2

2.將兩個事件看成兩個試驗

例2一個袋子中有標號為1，2，3，4的四個球，除標號外沒有其他差異.從中有放回地摸球兩次，設事件A=“第一次摸到1號球”，B=“第二次摸到2號球”，試分析事件A與B的關系.

解析：有學生錯誤地將韋恩圖繪制成圖2的形式，發(fā)現(xiàn)事件A與B不相交，根據(jù)命題1，認為A與B不獨立.錯誤的原因是事件A和事件B不是兩個試驗，而是一個試驗的兩個組成部分.即不能將事件A與B看成集合｛1，2，3，4｝的子集，而應該看成樣本空間Ω=｛（x，y）x，y∈｛1，2，3，4｝｝的子集，其中（x，y）表示“第一次抽到x號球，第二次抽到y(tǒng)號球”.故其正確的韋恩圖應畫成圖3的形式.從中可看出，事件A與B不互斥，且P（A）=，即事件A與B獨立.

圖3

事件A，B，C兩兩獨立與P（ABC）=P（A）P（B）P（C）的關系

教材中提到：當三個事件A，B，C兩兩獨立時，等式P（ABC）=P（A）P（B）P（C）一般不成立.用以下兩個例子來說明該結論.

通過上面兩個例子，可以看出事件A，B，C兩兩獨立與P（ABC）=P（A）P（B）P（C）沒有蘊含關系.下面結合韋恩圖給予一種直觀解釋.

命題3：當P（A）＞0，P（B）＞0，P（C）＞0時，若事件A，B，C兩兩獨立，則P（ABC）=P（A）P（B）P（C）等價于P（C）=P（CAB），等價于事件C與AB獨立，等價于事件C在樣本空間Ω中的概率與事件ABC在樣本空間AB中的概率相等.

例3中，如圖4所示，因為AB=｛（正，正）｝，ABC=｛（正，正）｝，所以P（CAB）=，即事件C與AB不獨立，所以P（ABC）≠P（A）P（B）P（C）.

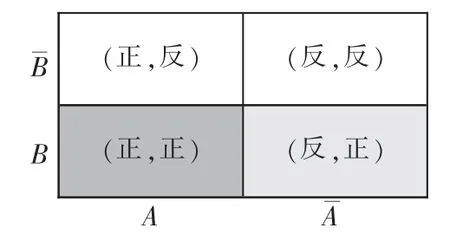
圖4

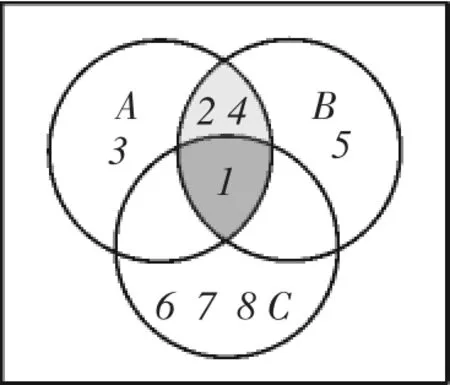
圖5

一般地，事件A，B，C兩兩獨立是指P（AB）=P（A）P（B），P（BC）=P（B）P（C），P（AC）=P（A）P（C）；事件A，B，C相互獨立是指A，B，C兩兩獨立，且P（ABC）=P（A）P（B）P（C）.從上面的例子可以看出，三個事件兩兩獨立不能推出它們是相互獨立的.

數(shù)學上有很多較為抽象的概念，通過某種工具或者某種方法讓其更直觀地表達出來，有利于降低初學者學習概念的難度，有利于初學者理解概念的含義和本質(zhì)，提高其學習數(shù)學的興趣.