關于新課標下復數教學的幾點建議
單如恒
江蘇省連云港高級中學 222000
高考對復數的考查要求并不高,往往是一個送分的選擇題,主要考查復數的概念、復數的運算和復數的幾何意義.基于此,教學中教師往往只對復數做應試層面的教學,而對復數的發展史、復數的內涵以及復數的應用涉及較少,這顯然不符合當前提高學生數學核心素養的教學目標的要求[1].那么,教師應如何教才能體現出新課標理念,才能為學生的終身發展服務呢?對此,筆者提出幾點復數教學建議,與同人共探.
回顧復數歷史,滲透數學文化
教數學,并非僅是教學生如何解題,還要讓學生了解數學知識的發展歷史.尤其是在“文化自信,以德樹人”的背景下,教師應積極把“數學教學”轉型為“數學教育”.基于此,復數教學,教師不能僅圍繞高考去教,而應把復數當成真正的數學知識去教.
任何一個數學知識的形成都經歷了歷史的洗禮,復數也不例外.教學中教師應該讓學生了解復數的發展歷史,培養學生對數學的情感.什么是復數?復數是實數與虛數的統稱.對于實數,學生在初中階段已經學過,因此這里的焦點是虛數.虛數真的是虛無縹緲的數嗎?教師可以帶領學生回顧虛數形成的這段歷史.在數學知識的發展史中,對虛數的假設是需要勇氣的,因為當時人們都無法接受,認為虛數是想象出來的一種數,是不存在的,但數學家們還是對虛數進行了長期的研究.首次認真研究虛數的是意大利數學家卡丹(Cardano,1501—1576),他生活在文藝復興時期,堪稱數學“怪杰”,他從1545年開始研究虛數,當時他把虛數叫做“詭辯量”.大約過了100年,著名數學家笛卡爾將這種數命名為虛數.后來又過了140多年,大數學家歐拉還是認為它是虛幻之數,于是用英文單詞imaginary(虛幻)的第一個字母i來表示它的單位,直到1831年大數學家高斯才對復平面作出了詳細說明,讓復數a+bi有了立足之地和用武之地,人們也才認識到復數.時至今日,復數在現代數學科技中有著廣泛的應用,無論是流體力學、熱力學、機翼理論,還是代數學、數論、微分方程,甚至是理論物理、彈性力學、天體力學,都能找到“復數”的身影.
數學課上講復數的發展史,是對歷史的尊重,也是提高學生數學素養的重要途徑.也許有人認為,只需簡單地討論方程x2+1=0在實數范圍內無解就可以輕松引入復數,但學生卻不能了解“真實的復數”,往往會認為復數只是一個符號.由此可見,教學中數學文化的滲透是何等重要,它有利于學生樹立正確的數學觀,學會用發展的眼光看待數學.
厘清復數概念,提高探究能力
數學概念的學習過程,一般分為六個階段——感知階段、想象階段、概括階段、形成階段、應用階段和結構階段,這六個階段體現了人們對事物的認知規律,也是學生學習復數概念的基本過程.復數對于學生來說是一個全新的概念,引入這個概念,教師可以引導學生在某些數學神奇的現象中發現和總結規律.
比如在復數概念教學中,筆者提出以下問題:
若x1,x2是方程x2+x+1=0的兩個根,則兩根之和是多少?兩根之積又是多少?
對于這個問題,部分學生往往不假思索,依據韋達定理馬上得出了答案:x1+x2=-1,x1·x2=1.而一些善于思考的學生則質疑:這個方程連實數根都不存在,哪兒來的兩根之和與兩根之積?韋達定理成立的前提條件是什么呢?是方程一定要存在實數根嗎?如果方程沒有實數根,它依然成立嗎?于是,筆者向學生提議:假如存在另外一種根(先不妨叫它為虛根),我們來驗證韋達定理是否成立.學生根據一元二次方程的求根公式得x1=,x2=,經檢驗,依然滿足韋達定理.但學生又產生了新的問題:如何求-3的算術平方根呢?筆者提示,假設i2=-1(i為虛數單位),問題即可迎刃而解.于是學生求得x1=,同時發現,方程x2+x+1=0雖然不存在實數根,但它存在虛根,這兩個虛根同樣滿足韋達定理.筆者提示,這兩個虛根其實就是兩個虛數.于是,趁勢引出復數a+bi(a,b∈R)的有關概念——什么是復數的實部和虛部,什么是實數,什么是虛數,什么是純虛數,什么是復數,并分別探討當a+bi(a,b∈R)為實數或純虛數時實部與虛部滿足的條件.
在探討的過程中,學生提出了疑問:虛數到底存在不存在?如果存在,它表示什么呢?可見學生很想知道復數的幾何意義.于是,筆者引出了復平面概念,指出a+bi(a,b∈R)表示的是復平面上的點(a,b),學生很快發現,實數表示的點在x軸上,純虛數表示的點在y軸上,虛數表示的點在四個象限內.接著,筆者引導學生回頭看的幾何意義,學生發現這兩個根表示的點都在以原點為圓心的單位圓上,可見“虛根不虛”.再接著,筆者要求學生在復數范圍內解方程x3-1=0.由于上述問題的鋪墊,學生很快解得方程的三個根,分別是1,和,并驚奇地發現這三個根表示的點剛好把以原點為圓心的單位圓三等分,于是又得到了兩個非常有用的結論:若ω=-則有①ω2+ω+1=0;②ω3=1.
概念是數學學習的基礎,概念的產生都有著豐富的背景.筆者認為,從具體的背景中引導學生探究數學概念,比教師和盤托出數學概念更有利于學生對數學概念的建構.對于復數的概念課,或許有些教師認為不要提及復數的幾何意義,但筆者認為復數的幾何意義與復數的概念密不可分,結合復數的幾何意義看復數的概念比單純研究復數的概念更有利于學生理解.
強化復數應用,提升數學素養
新課標對復數教學的要求雖然不高,考試也只是要求學生掌握復數的概念以及基本運算和幾何意義的簡單應用,一般不會涉及難題,但從培養學生的核心素養的角度來看,筆者認為復數教學不能僅以考試要求為原則,還應通過強化復數應用,提高學生的數學素養.尤其是教材的選學內容——復數的三角表示,為復數教學指明了方向[2].雖然是選學內容,但它能溝通復數的幾何意義與三角函數之間的聯系,筆者認為不妨將它當成必學內容.
繼平面向量后,復數幫我們建立了一座聯系代數與幾何的“橋梁”,教師可以通過這座“橋梁”,幫助學生溝通數學知識間的聯系,引導學生建構獨特的復數法.下面舉例說明:

對于第(1)問,可以引導學生把每一個根號都看成復數的模,通過構造復數,利用復數的幾何意義解決問題:

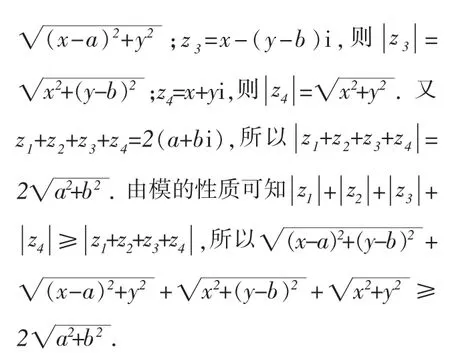
對于第(2)問,同樣可以通過構造復數,利用復數的三角表示來解決數列問題:

由此可見,巧妙利用復數,可以創造性地解決一些比較復雜的問題,這些源于課本又高于課本的數學方法,也應該成為教學重點.雖然從應試角度來看,對復數方法拓展性的應用似乎沒有必要,但從學生的終身發展來看,在復數教學中,這種數學思維的培養十分重要,也十分必要.因為無論學習什么,只有站得高才能看得遠,“會當凌絕頂”,方可“一覽眾山小”.
以上三點建議,是基于學生的數學核心素養提出的,筆者認為,真正的數學教育應擺脫應試教育的束縛,走出“考什么,教什么”的誤區.應忠于教材,又不囿于教材,以培養學生的關鍵能力,促進學生終身發展.

