二維圓柱對旋轉單極子點源的聲散射

薛絲丹，錢振昊，何嘉華，劉秋洪

（1.西北工業大學翼型葉柵空氣動力學重點實驗室，西安 710072；2.中國空氣動力研究與發展中心氣動噪聲控制重點實驗室，四川綿陽 621000）

在過去幾十年中，旋轉葉片產生的氣動噪聲問題一直是航空聲學的研究熱點，目前已經在理論分析和數值計算方面取得一些重要的成果。早期理論研究，包括Ffowcs Williams 等[1]、Lowson[2]以及Morfey 等[3]的工作，都傾向于將旋轉葉片噪聲源簡化為理想的旋轉點源，以點源模型預測旋轉葉片噪聲。另一方面，越來越多的研究者從計算流體動力學（CFD）和聲比擬理論出發，將旋轉葉片噪聲源視為一系列旋轉運動點源分布，采用時域[4-5]或頻域[6-7]數值方法預測噪聲。

研究旋轉點源的聲場精確解有助于發展高精度的噪聲數值預測方法。吳九匯等[8]最早應用球諧級數展開方法建立了旋轉點聲源在自由空間中的理論解析解。Poletti[9-10]提出了旋轉二維和三維單極子點源聲輻射精確時域球諧解。Carley[11]提出了一種用級數展開法預測旋轉單極子點源輻射噪聲的理論模型。Mao等[12]利用球坐標系和柱坐標系級數展開法，推導了旋轉單極子和偶極子輻射聲場的精確解。進一步地，Mao 等[13]推導了旋轉四極子點源聲輻射精確解。這些理論模型都假設點源在自由場中旋轉。

實際應用中，旋轉點源輻射的聲波會因周圍聲學邊界條件的存在而發生散射效應，比如機翼和機身等結構對螺旋槳噪聲的散射，使得實際聲場與自由空間輻射聲場存在明顯差異。在已發表的學術文獻中，使用理論解析方法對結構的聲散射進行了有限的關注。Glegg[14]將螺旋槳聲源建模為旋轉偶極子點聲源、中心體簡化為無限長的剛性圓柱體，得到一個預測螺旋槳遠場聲壓的公式，其中包含了輪轂的散射。Kingan 等[15]擴展了Glegg 的工作以評估中心體散射對開式轉子噪聲的影響。Hanson等[16]提出了一種計算飛行器機身散射開式轉子噪聲的方法，機身被簡化為無限長聲學剛性圓柱體。McAlpine等[17]應用Hanson 等的分析進一步評估機身散射對旋轉單極子或偶極子點源以及開式轉子噪聲的影響。Kingan等[18]也進行了類似的研究。毛義軍等[19]對旋轉聲源輻射噪聲和邊界散射噪聲的預測方法進行了綜述。

理論模型對實際物理問題進行了太多簡化，需要發展可靠的數值方法以提高旋轉點源的聲場預測精度。本文基于點源模型，利用邊界積分方法研究二維聲學邊界對旋轉點源的聲散射效應。為驗證數值方法的可靠性，對二維圓柱的聲散射進行了理論建模分析。

1 聲散射計算的邊界積分方法

觀察點與源點的位置和時間分別用x和y以及t和τ表示。如圖1所示，剛性固體邊界S附近有一簡諧振動角頻率為ωs的單極子點源q（y,τ），以角頻率ωr繞o點逆時針旋轉，其初始相位和振幅分別為0和1，即點源可表示為：

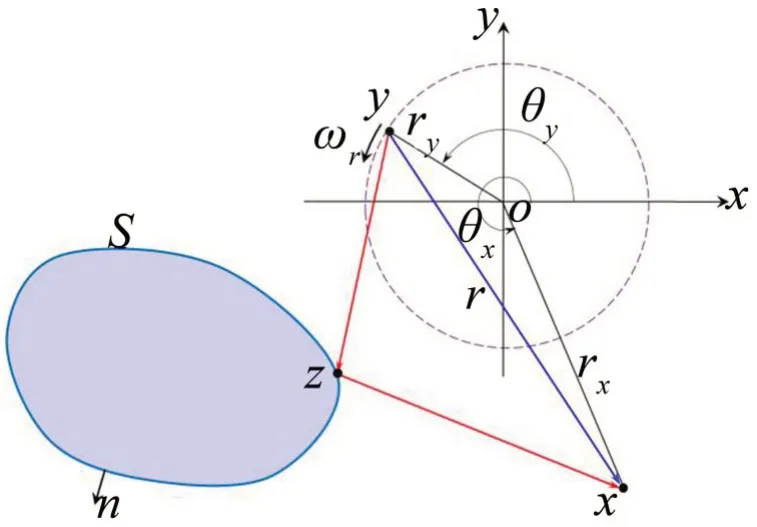
圖1 旋轉點源聲傳播示意圖

那么，時域下的聲學控制方程為：

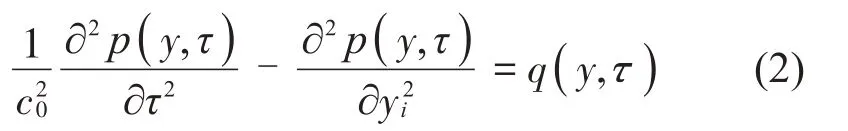
式中：c0為聲傳播速度。在剛性固體邊界上，聲場應滿足聲學硬邊界條件：

方程式（2）的基本解為自由空間格林函數G0（x,y,t-τ ），滿足方程（4）：

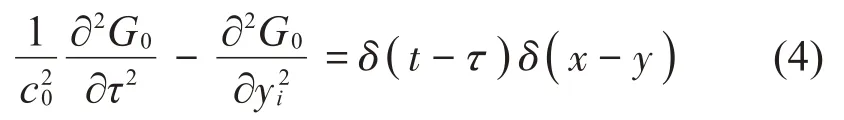
利用方程式（2）～方程式（4）可得到：

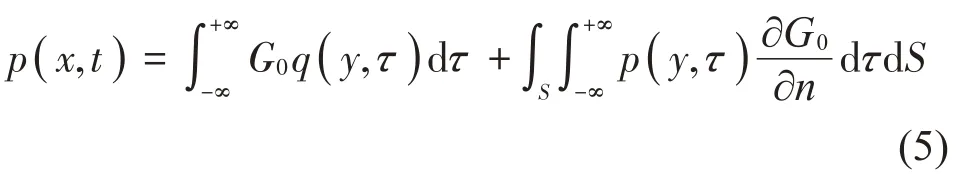
根據Fourier變換定義：

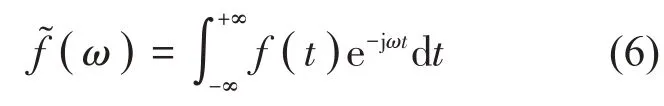
頻域自由空間格林函數為：

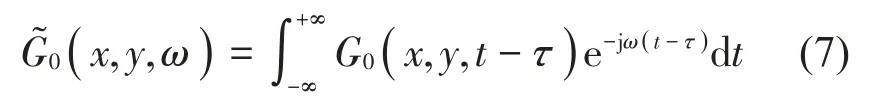
因此方程式（5）可在頻域下寫成：

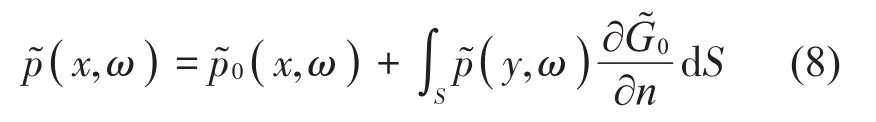
式中右端兩項分別為入射聲和散射聲。

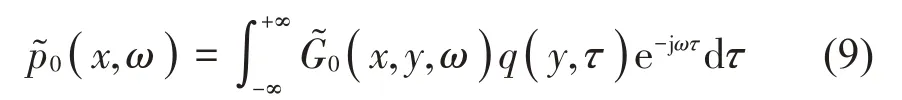
以點源旋轉中心為坐標原點建立極坐標系，觀察點x和源點y的位置分別為（rx,θx）和（ry,θy），假設點源的初始位置為θ0，則有：

假設聲傳播介質靜止、均勻，對二維聲傳播問題，頻域自由空間格林函數為：

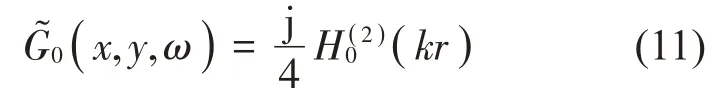
其級數展開形式為：

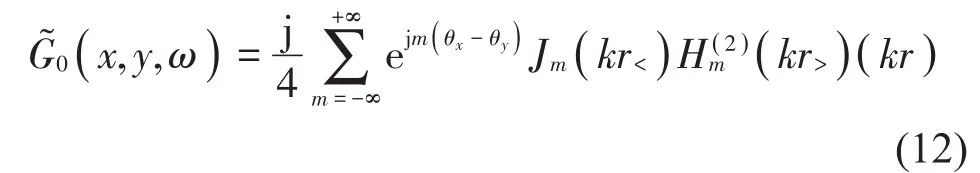
其中：Jm（ · ）表示m階Bessel 函數，Hm（2）（ · ）表示m階第二類Hankel函數，r＜=min（rx,ry），r＞=max（rx,ry），k=ω c0為聲學波數。將式（1）、式（10）和式（12）代入方程式（9）得到：

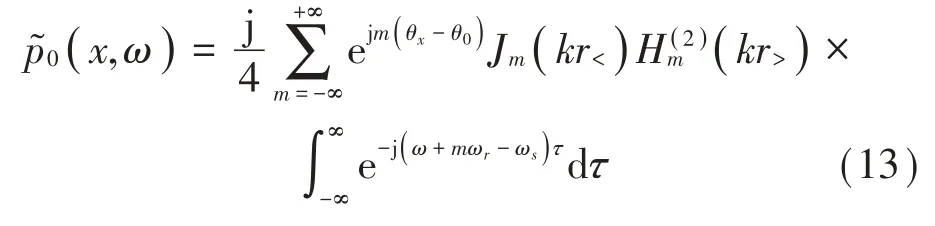
利用Dirac函數性質：

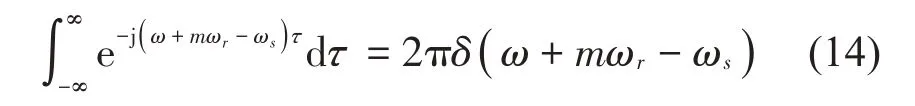
得到聲入射的表達式為：

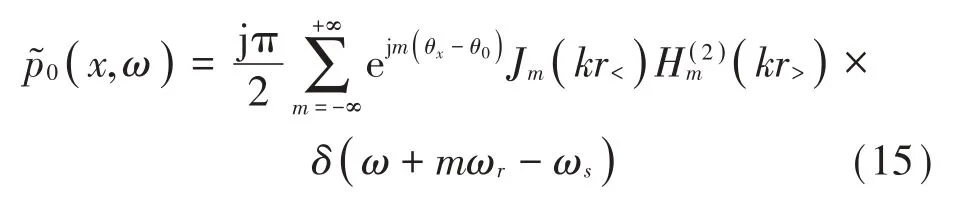
將散射邊界離散為N個網格單元，采用等參邊界元方法求解方程（8）以獲得散射邊界上的聲場。當觀察點置于散射邊界時，積分方程式（8）可離散為一系列線性方程組：

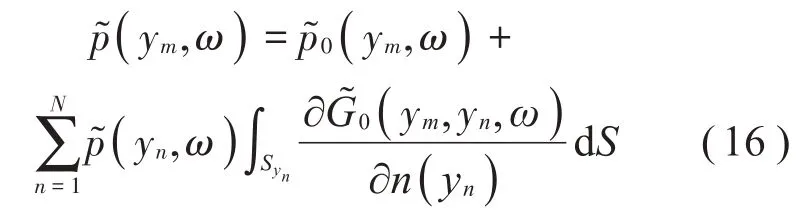
寫成矩陣形式為：

其中：

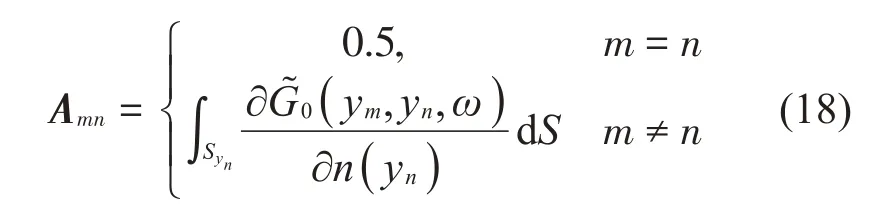
2 圓柱聲散射理論解析解

二維圓柱幾何形狀簡單，易獲取散射場的理論解析表達式。將觀察點的聲學壓力場分解為自由入射聲場和圓柱散射聲場兩部分，前者可由式（15）決定，還需得到后者的解析表達。類似于式（9），假設圓柱聲散射的表達為：

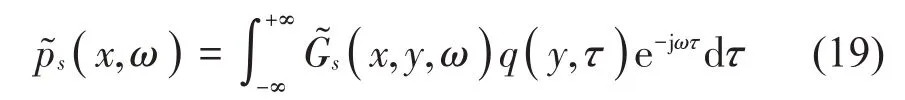
2.1 點源與圓柱同軸旋轉

點源q（y,τ）繞圓柱同軸旋轉如圖2 所示，假設散射格林函數可表示為：

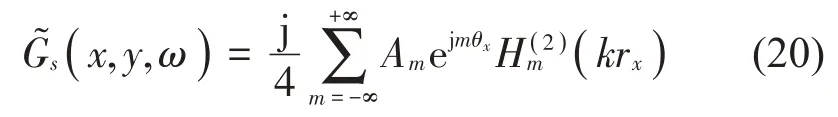
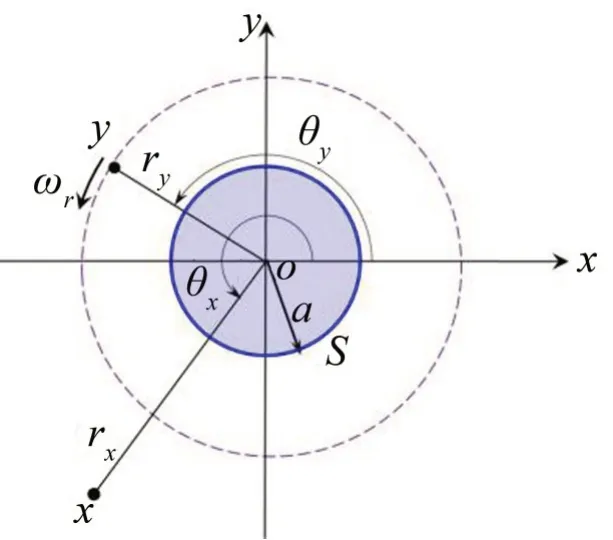
圖2 點源繞圓柱同軸旋轉示意圖

當觀察點位于圓柱表面時，將式（12）和式（20）代入聲學邊界條件（3），可解得：

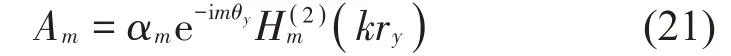
式中：

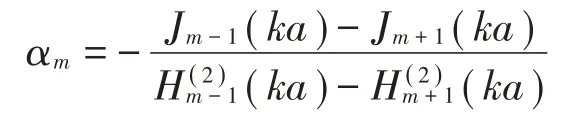
即有：

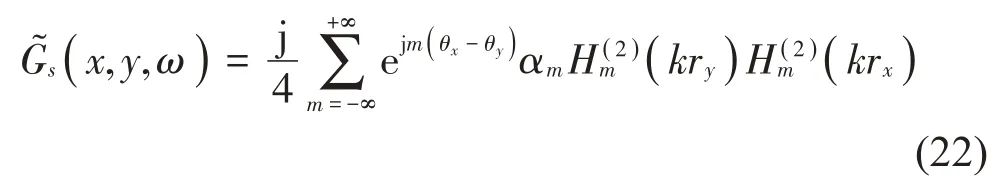
將式（1）、式（10）和式（22）代入式（19），利用式（14）得到：

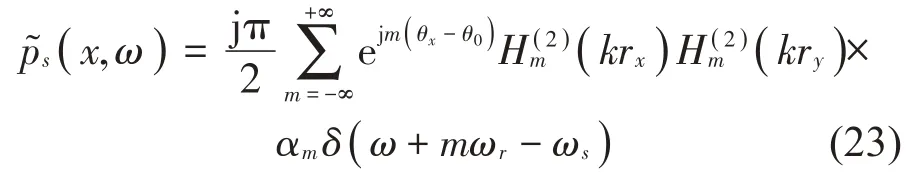
2.2 點源與圓柱異軸旋轉

如圖3 所示，二維圓柱附近有一旋轉單極子點源q（y,τ），其旋轉中心與圓柱中心的距離為d，以點源旋轉中心點為坐標原點建立極坐標系，對應的觀察點x和源點y的位置分別為（rx,θx）和（ry,θy）；同時以圓柱中心點為原點建立另一極坐標系，對應觀察點x位置為當觀察點位于圓柱表面時，顯然有rx＞ry和＜d。根據Graf加法定理，

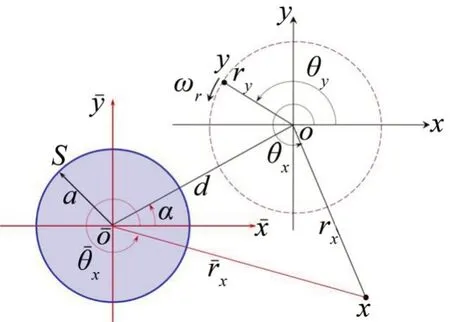
圖3 點源與圓柱異軸旋轉示意圖

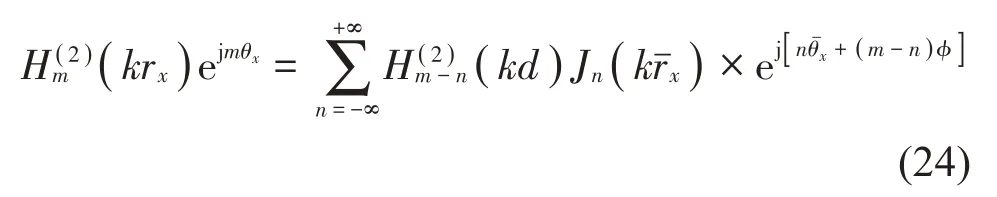
可將自由空間格林函數改寫為：

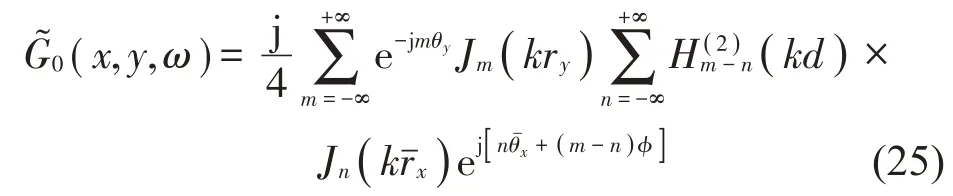
其中：?=π+α。

進一步令：

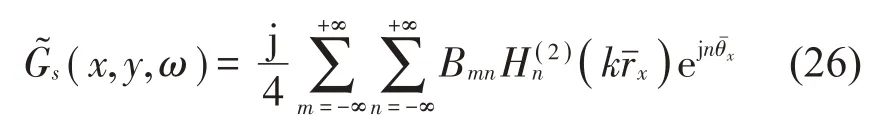
利用式（1）和式（10），分別將式（25）代入式（9）、式（26）代入式（19），根據邊界條件式（3）和關系式（14），可解得：

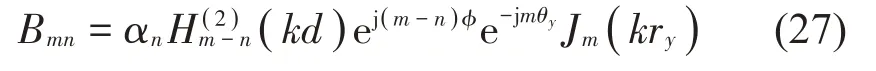
式中：

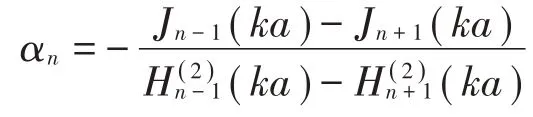
從而散射格林函數可寫為：

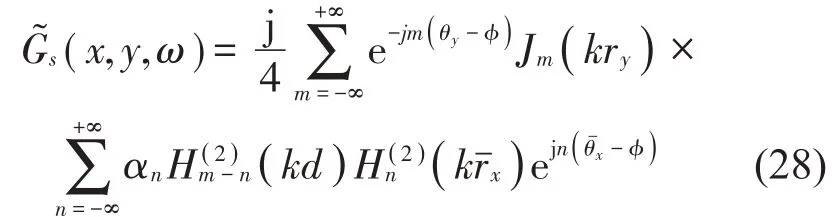
將式（28）代入式（19），積分可得：

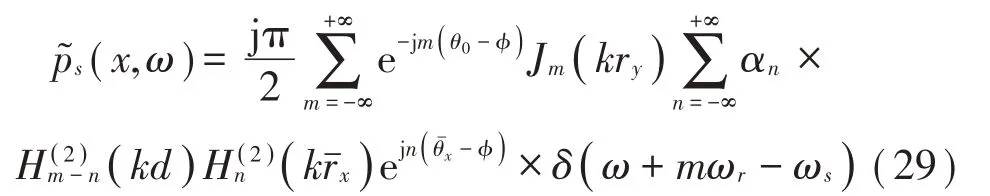
旋轉單極子源的解對m具有無限項，在實際應用過程中應以截斷方式采用有限項計算，截斷項數M與觀察點感興趣的聲波頻率ω有關，當ω小于源諧振頻率ωs時,截斷項數應保證ω＜Mωr-ωs，也就是；當ω大于源諧振頻率ωs時，應滿足。除此之外，根據Bessel 函數的指數衰減性質，M不小于，[ · ]表示向上取整數。基于上述的分析，截斷數M應該滿足：

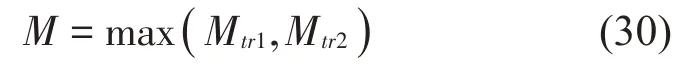
3 二維圓柱算例驗證

采用等參邊界元方法計算單極子點源與圓柱同軸和異軸旋轉的聲輻射特性，將結果與理論解析解對比，驗證數值方法的正確性。取圓柱半徑a=1.0 m，單極子點源的初始位置θ0=0°，其諧振頻率和旋轉頻率分別為

3.1 點源與圓柱同軸旋轉算例驗證

如圖2 所示，取ry=1.5 m。采用邊界元方法進行聲傳播計算時，需要足夠的網格數量以保證數值結果與網格無關。在圓柱表面均勻分布180個網格單元，對500 Hz 以下的聲波，一個波長范圍內不少于20個網格單元，可以滿足網格無關性要求。數值積分采用四點高斯積分方法，線性方程組的求解采用全選主元高斯消去法。

圖4為觀察點（rx=10 m,θx=0°）的聲壓幅值譜，邊界元數值解與理論解吻合一致。與固定點源產生的單頻聲場不同，旋轉點源因存在多普勒效應，產生的噪聲分布在一系列離散頻率上，離散頻率滿足關系式ω=ωs-mωr，其中m為諧波階次；最高峰值頻率為f=160 Hz，對應的諧波階次為m=4。在低頻（小于100 Hz）和高頻（大于400 Hz）處，聲壓幾乎為0。

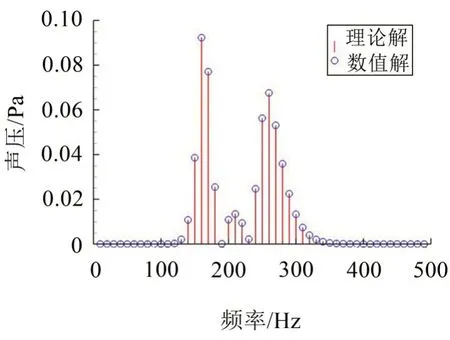
圖4 點源繞圓柱同軸旋轉時觀察點聲壓幅值譜（rx =10 m,θx =0°）

圖5為圓柱表面上160 Hz聲壓幅值指向性分布的邊界元數值結果與理論解析結果的對比圖。對不同的網格單元，數值解與理論解的一致性非常好。對相同極半徑的觀察點，聲壓的幅值是相同的，呈現出典型的單極子聲場特性。

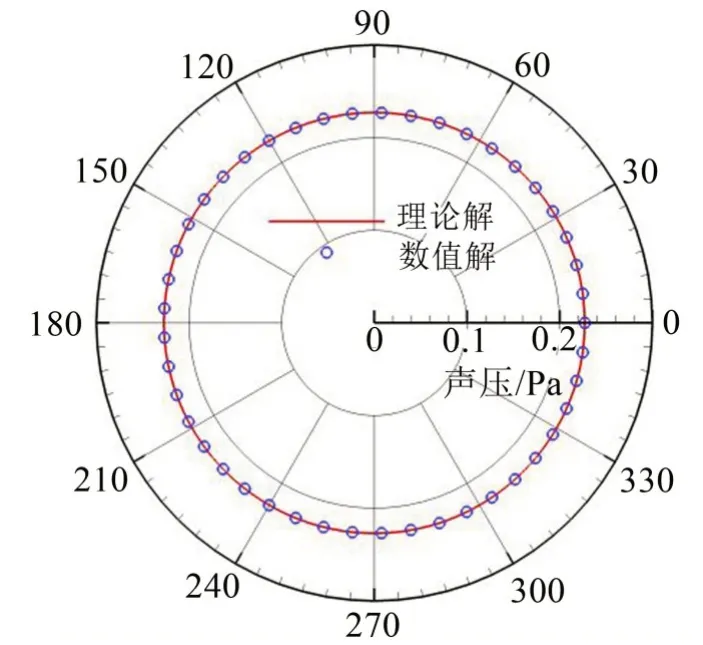
圖5 點源繞圓柱同軸旋轉圓柱表面160 Hz聲場指向性分布

圖6 為邊界元方法計算得到的140 Hz、200 Hz和260 Hz總聲壓實部的空間分布云圖，對應的諧波階次分別為m=6、m=0 和m=-6。從圖中可以看到，m=0的聲波呈同心圓狀向外輻射；而m≠0的聲波則以螺旋狀向外輻射，螺旋瓣的數量與 |m|相同，且m＞0 時螺旋瓣的方向與點源旋轉方向相反，而m＜0 時則相同。

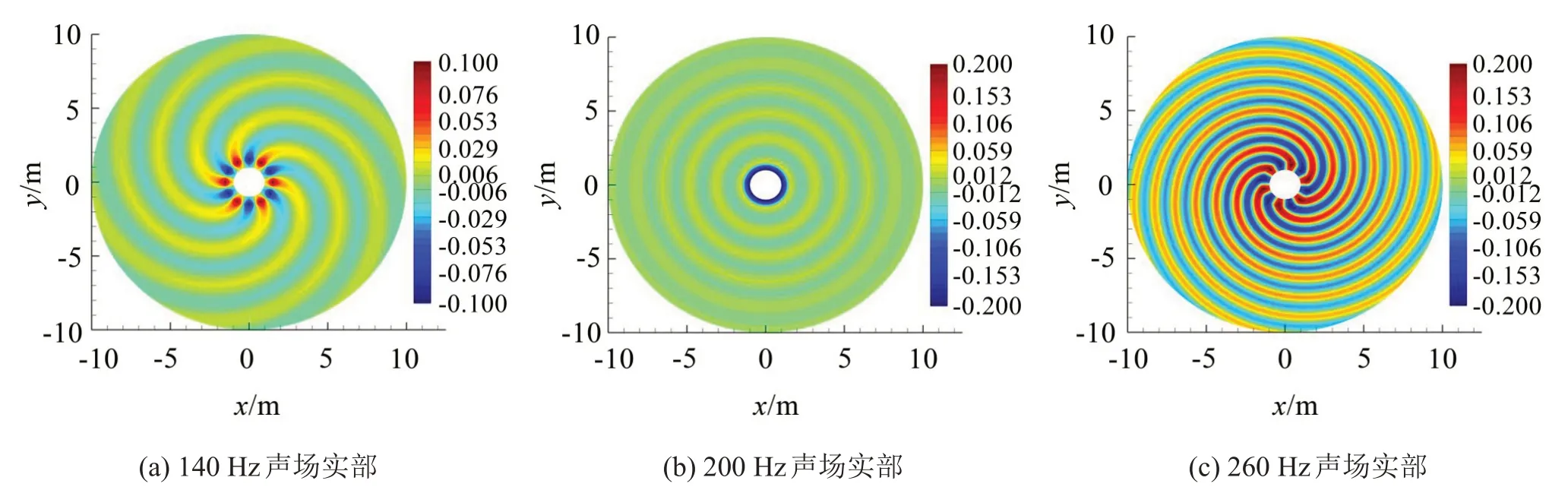
圖6 點源繞圓柱同軸旋轉時聲場分布云圖

3.2 點源與圓柱異軸旋轉算例驗證

對如圖3 所示的點源與圓柱異軸旋轉算例，選取ry=0.5 m、0°和d=2.0 m。邊界元方法的數值計算采用與同軸旋轉算例一致的網格，以及相同的數值積分和線性方程組求解方法。

圖7 為觀察點（=10 m，=0°）的聲壓幅值譜，邊界元數值解與理論解再次吻合一致。異軸旋轉點源產生的噪聲分布在一系列離散頻率上，這與同軸旋轉的頻譜特性相似，最高峰值頻率為f=210 Hz，對應的諧波階次為m=-1。

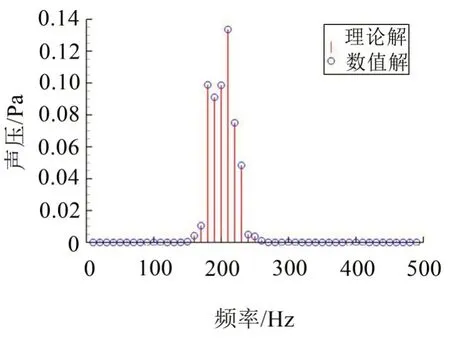
圖7 點源繞圓柱異軸旋轉時觀察點聲壓幅值譜（=10 m, =0°）

在=10 m 的圓周上取不同的觀察點，將數值計算的聲壓幅值與理論解析結果進行對比。圖8為210 Hz聲場的聲壓幅值指向性分布，對不同的觀察點，數值解與理論解是一致的。由于圓柱對聲波的散射作用，聲場的空間分布趨于復雜化，不像同軸旋轉那樣具有顯著的規律特征。

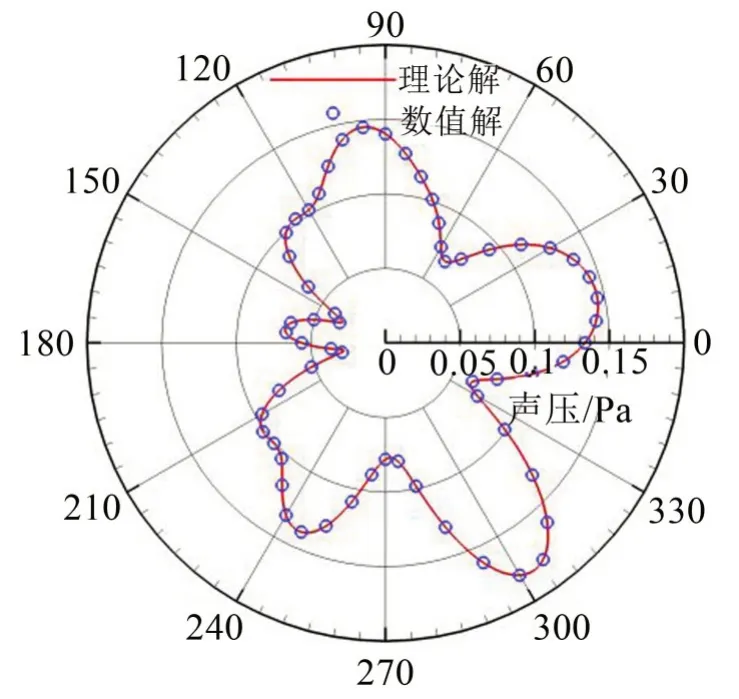
圖8 點源繞圓柱同軸旋轉時聲場指向性圖（ =10 m, f =210 Hz）

圖9為邊界元方法計算得到的210 Hz聲場的自由入射聲壓、圓柱散射聲壓和總聲壓實部的空間分布云圖。入射聲波以明顯的螺旋狀向外輻射，這是由點源的旋轉運動特性決定的。與同軸旋轉算例不同的是，圓柱對異軸旋轉點源入射聲波的散射不再具有單極子的螺旋狀特性，而呈現顯著的偶極子特征，使得總聲場在多個方向存在強傳播。

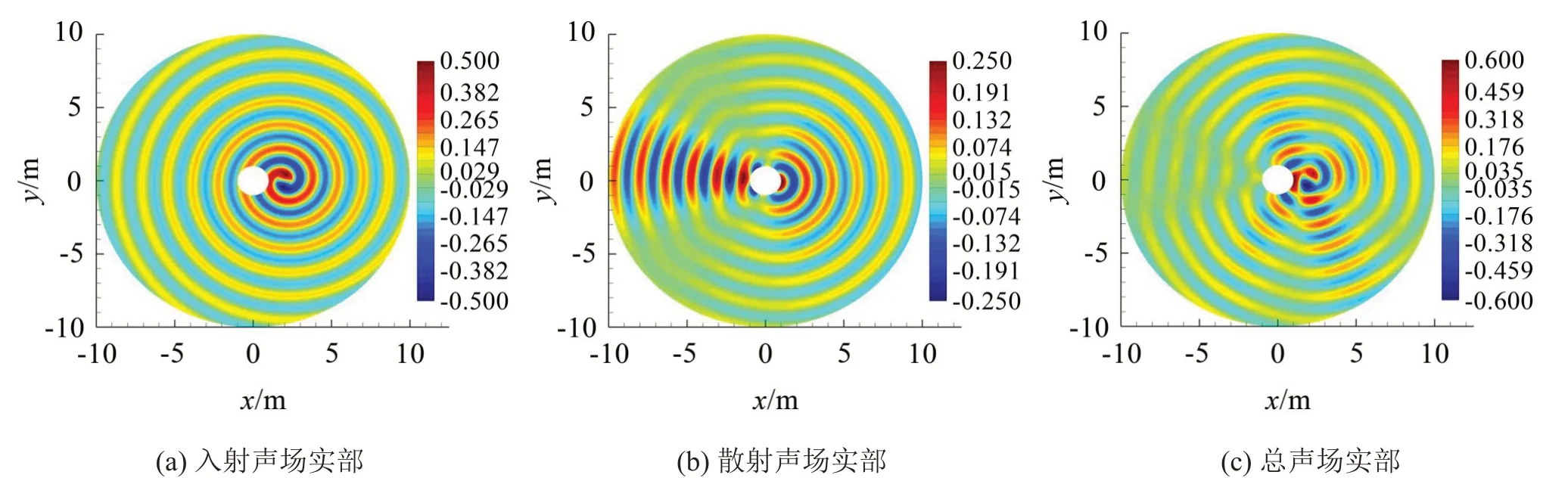
圖9 點源繞圓柱異軸旋轉時210 Hz聲場分布云圖

4 結語

對任意形狀的剛性散射邊界，利用自由空間格林函數的級數展開式求解線性聲學波動方程，建立了旋轉單極子點源聲輻射的頻域邊界元數值計算方法。同時，根據貝塞爾函數的加法定理，推導了點源與二維剛性圓柱同軸、異軸旋轉狀態下的聲場理論解析表達式。

對點源與圓柱同軸、異軸旋轉兩個算例，邊界元方法的數值解均與理論解析解吻合一致。點源向外輻射聲波的頻率由點源諧振頻率、旋轉頻率和諧波階次共同決定。對同軸旋轉算例，諧波階次為0 的聲波以同心圓狀向外輻射，不為0 的聲波則以螺旋狀向外輻射，螺旋瓣的數量與諧波階次的絕對值相同。對異軸旋轉算例，圓柱的聲散射呈現顯著的偶極子特征，聲場的指向性復雜，不像同軸旋轉算例具有顯著的螺旋輻射特征。

在后續的研究中，將進一步考慮旋轉偶極子、四極子點源的聲輻射特性和運動介質的影響，以及將二維聲傳播的研究結果推廣到三維聲學問題的研究。