正負(fù)剛度并聯(lián)隔振系統(tǒng)建模與性能分析

朱 亮，周 濤，吳乙萬，白鴻柏，湯 宇

（1.福州大學(xué)機(jī)械工程及自動化學(xué)院金屬橡膠工程研究中心，福州 350116；2.中國人民解放軍92578部隊，北京 100161）

振動是自然界最普遍的現(xiàn)象之一，在許多工程技術(shù)領(lǐng)域中，振動是有害的，為了減小工程中的有害振動，需要對減隔振方法進(jìn)行相關(guān)研究[1-3]，常用的方式是在振源和基礎(chǔ)之間安裝隔振器。隔振器一般分為被動隔振器和主動控制隔振器，被動隔振器由于其結(jié)構(gòu)簡單、經(jīng)濟(jì)性好而被廣泛運用。然而傳統(tǒng)的被動線性隔振系統(tǒng)僅對中-高頻帶的振動具有較好的隔振效果，對低頻振動卻難以有效控制[4-6]。由傳統(tǒng)被動線性隔振理論可知，只有當(dāng)外界干擾的頻率大于隔振系統(tǒng)固有頻率的 2 倍時[7]，隔振器才會起到隔振作用。雖然通過降低隔振系統(tǒng)的剛度能夠降低其固有頻率，拓寬隔振頻帶，但這會導(dǎo)致隔振系統(tǒng)的剛度降低，使隔振系統(tǒng)的承載力和穩(wěn)定性變差。從而導(dǎo)致傳統(tǒng)的被動隔振器在解決重型裝備的低頻減振問題時無法得到有效的應(yīng)用。

正負(fù)剛度并聯(lián)隔振系統(tǒng)是在線性隔振系統(tǒng)的基礎(chǔ)上并聯(lián)一個負(fù)剛度元件，負(fù)剛度元件可以降低隔振系統(tǒng)的剛度，由正剛度彈簧提供承載力。這種隔振系統(tǒng)不僅具有較低的固有頻率，同時還具有較高的承載能力，在重載低頻工況下具有良好的減振能力，彌補了傳統(tǒng)被動隔振系統(tǒng)的不足。

近年來，許多學(xué)者對正負(fù)剛度并聯(lián)機(jī)構(gòu)進(jìn)行了理論與試驗研究，并研制出了多型實用的隔振器。Meng等[8-9]將單片碟形彈簧與線性彈簧并聯(lián)，設(shè)計了一種準(zhǔn)零剛度（Quasi-Zero Stiffness，QZS）隔振器，并研究了QZS 隔離器的特性以及過載或欠載對其隔離性能的影響；Liu等[10]設(shè)計了一種壓縮桿式準(zhǔn)零剛度隔振單元，建立了6自由度準(zhǔn)零剛度隔振平臺；Wu 等[11]利用三塊方形永磁鐵的相互作用力得到非線性的負(fù)剛度結(jié)構(gòu)，并對其負(fù)剛度特性進(jìn)行了分析；王迎春等[12]研制了雙環(huán)永磁體型和三磁體型高靜低動隔振器，分析諧波位移激勵下隔振器的隔振性能，并與等效線性隔振系統(tǒng)的傳遞特性進(jìn)行對比，驗證了隔振系統(tǒng)低頻隔振性能的優(yōu)越性；汪宏斌等[13]介紹了兩種典型的正負(fù)剛度并聯(lián)超低頻非線性隔振器，研究了兩種隔振器的非線性剛度參數(shù)對隔振器準(zhǔn)零剛度特性的影響；時培成等[14]利用連桿彈簧負(fù)剛度機(jī)構(gòu)與正剛度彈性元件并聯(lián)，設(shè)計了一種具有準(zhǔn)零剛度的座椅懸架系統(tǒng)，基于NSGA-Ⅱ算法對懸架系統(tǒng)進(jìn)行結(jié)構(gòu)參數(shù)優(yōu)化，有效減小了振動響應(yīng)的幅值；鄧澤華等[15]在線性隔振系統(tǒng)中并聯(lián)負(fù)剛度雙穩(wěn)定復(fù)合材料層合板，使系統(tǒng)在靜平衡位置附近處的剛度降低。文獻(xiàn)調(diào)研結(jié)果表明，已有隔振系統(tǒng)僅在平衡位置有較低的固有頻率，無法承受重載、大幅度變形，且需與額外的阻尼器配合使用。現(xiàn)有方案無法兼顧大載荷、大變形、低頻、阻尼耗能等性能，因此需要對正負(fù)剛度并聯(lián)機(jī)構(gòu)進(jìn)行進(jìn)一步研究。

本文針對重型裝備的低頻減振問題，考慮到隔振系統(tǒng)的小空間、大行程要求，選用對合碟形彈簧作為負(fù)剛度元件，選用伸長比較大的矩形彈簧作為正剛度彈性元件，設(shè)計了一種具有低剛度特性的重載低頻隔振器，建立正負(fù)剛度并聯(lián)隔振系統(tǒng)簡化模型及其動力學(xué)微分方程，通過數(shù)值計算和仿真分析驗證隔振系統(tǒng)的動態(tài)性能，搭建力傳遞率測試平臺，驗證所建動力學(xué)模型的正確性與合理性。

1 正負(fù)剛度并聯(lián)機(jī)構(gòu)剛度匹配

1.1 碟形彈簧靜力學(xué)特性

圖1為碟形彈簧的結(jié)構(gòu)示意圖，h為碟簧的自由高度，H為碟簧的總高，t為碟簧的厚度，d、D分別為碟簧的內(nèi)徑和外徑。碟簧具有理想的非線性特性，其計算方法一般采用美國學(xué)者Almen 和Laszlo于1936年提出的近似解法（簡稱A-L 解）[16]，本文選用的為無支撐面的碟簧，則其載荷位移關(guān)系式為：

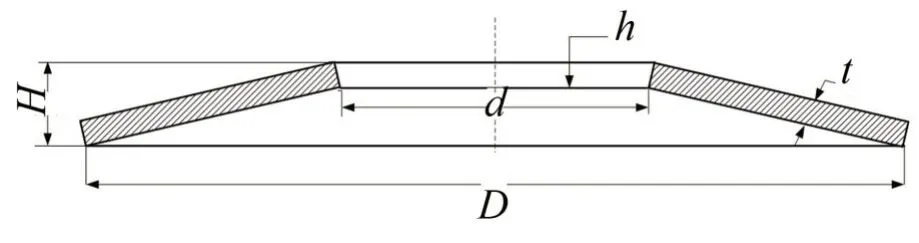
圖1 碟形彈簧示意圖

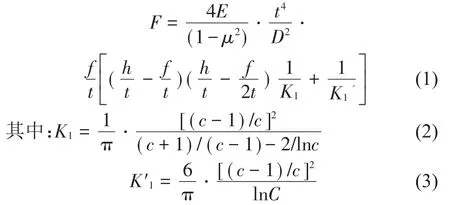
F為碟簧所承受的載荷，E為彈性模量，μ為泊松比，f表示碟簧的變形大小，通常不超過0.75h～0.8h，C為碟簧外徑與內(nèi)徑之比，C=D/d，K1與K′1表示兩個系數(shù)，通常對于C=1～4，有K1=K′1，因此式（1）可以簡化為：

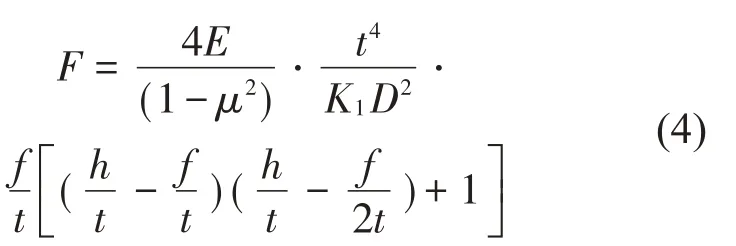
載荷F對變形f進(jìn)行求導(dǎo)，求得單片碟簧的剛度為：

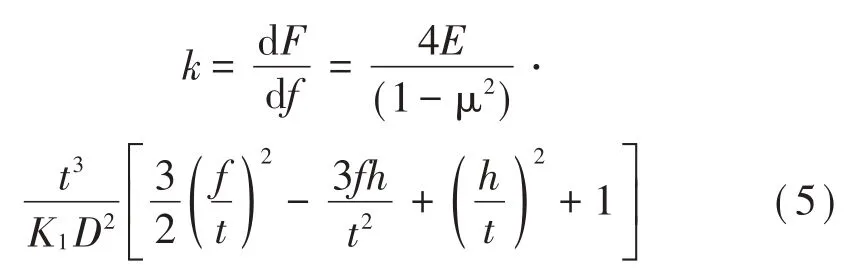
令f/t=η，高厚比h/t=?給定系數(shù)：，則碟簧的剛度計算公式為：

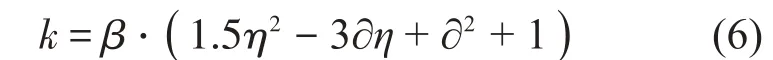
由式（6）可得，碟簧的載荷變形特性曲線受高厚比?的影響最大，如圖2所示。具體為：

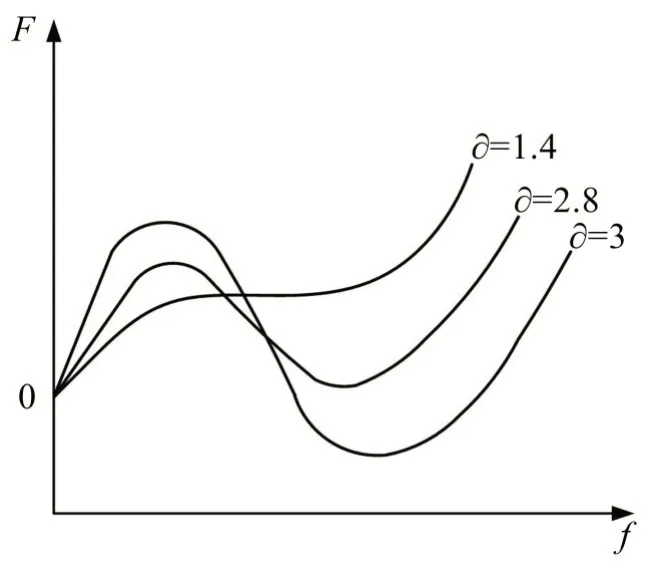
圖2 碟簧特性曲線與高厚比的關(guān)系

（1）當(dāng)?≈時，特性曲線將會出現(xiàn)一段接近水平的區(qū)域，在此區(qū)域內(nèi)碟簧的剛度接近于零；

（2）當(dāng)?＞時，會逐漸出現(xiàn)負(fù)剛度區(qū)域；

（3）當(dāng)?＞時，負(fù)剛度區(qū)域?qū)兊酶蟆?/p>

1.2 正負(fù)剛度并聯(lián)機(jī)構(gòu)

如圖3 所示，將對合碟形彈簧與正剛度矩形彈簧并聯(lián)，由對合碟簧組和矩形彈簧共同承載。

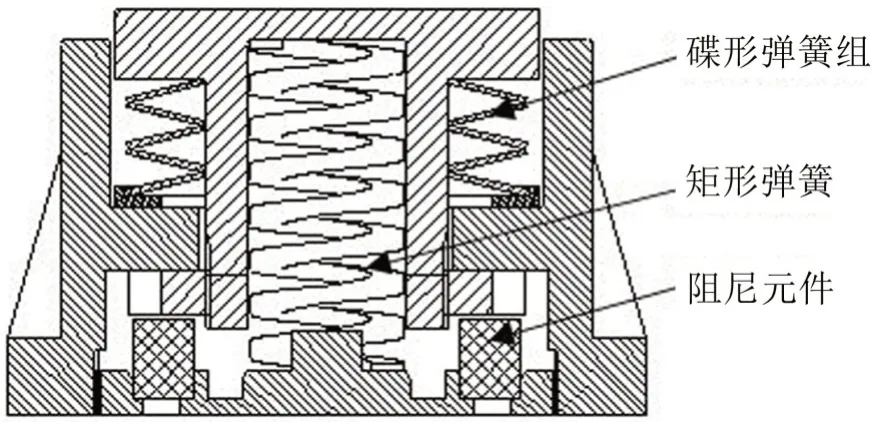
圖3 正負(fù)剛度并聯(lián)隔振系統(tǒng)

對合碟簧組各碟簧之間相互串聯(lián)，忽略各碟簧之間的摩擦力，故對合碟形彈簧組所承受的載荷Fp,總變形量fp和剛度Kp分別為：

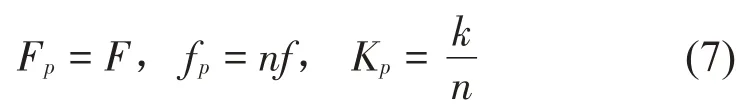
其中：n表示對合碟簧的個數(shù)。正負(fù)剛度并聯(lián)隔振系統(tǒng)的載荷位移關(guān)系式為：

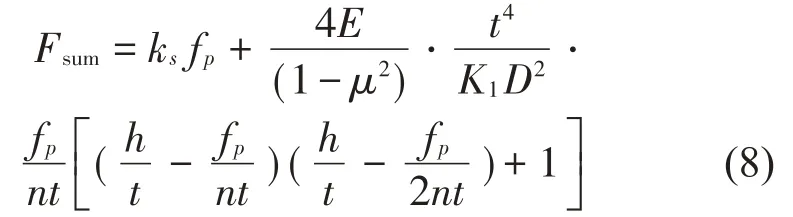
正負(fù)剛度并聯(lián)隔振系統(tǒng)的剛度ksum為：

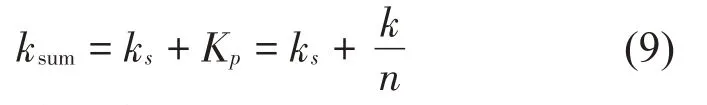
將式（6）代入式（9）得：

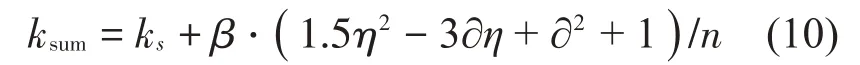
2 隔振系統(tǒng)動力學(xué)分析

2.1 等效彈簧力

本文選定碟簧的參數(shù)：外徑D=100 mm，內(nèi)徑d=50 mm，厚度t=1.75 mm，內(nèi)錐高度：h=3.4 mm，采用A型無支承面彈簧，并且采用5 片碟簧對合串聯(lián)，與矩形彈簧并聯(lián)。材料彈性模量E=2.06×105，泊松比μ=0.3，根據(jù)其內(nèi)外徑之比C=D/d=2 可以查表得到[16]系數(shù)K1=0.694。矩形彈簧的剛度ks=157 N/mm。

將上述選定參數(shù)帶入式（8），可以得到正負(fù)剛度并聯(lián)機(jī)構(gòu)的載荷-位移曲線，為便于對隔振系統(tǒng)進(jìn)行動力學(xué)分析，利用MATLAB擬合工具箱對其進(jìn)行擬合，可以得到隔振系統(tǒng)的等效彈簧力，設(shè)等效彈簧力為Fk，擬合的等效彈簧力參數(shù)如表1所示。

表1 等效彈簧力參數(shù)

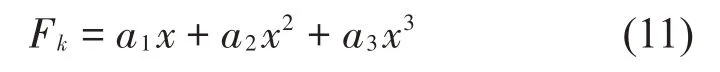
如圖4 所示，參數(shù)擬合的等效彈簧力與目標(biāo)載荷位移曲線具有較好的重合度，可用于正負(fù)剛度并聯(lián)結(jié)構(gòu)的動力學(xué)分析。

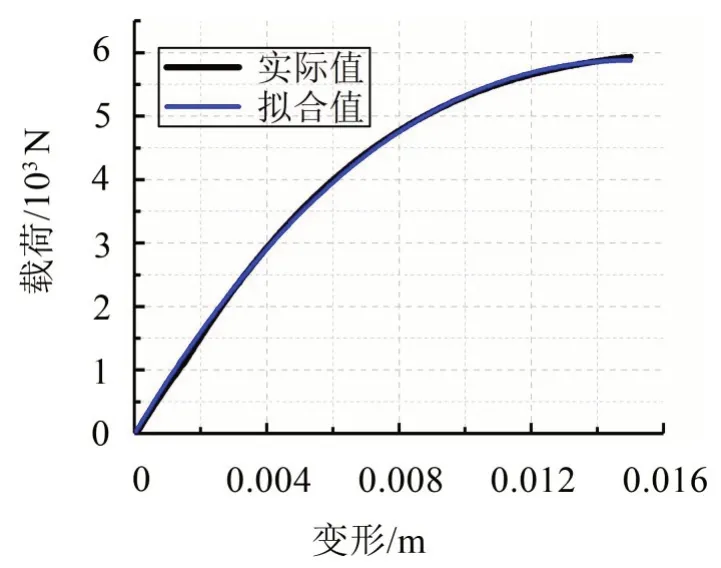
圖4 MATLAB擬合工具箱擬合結(jié)果

2.2 隔振系統(tǒng)數(shù)學(xué)模型

正負(fù)剛度并聯(lián)隔振系統(tǒng)的簡化模型如圖5 所示。質(zhì)量M表示需要進(jìn)行隔振的各種振源（如設(shè)備、工作機(jī)械等），正剛度矩形彈簧k+和負(fù)剛度碟形彈簧k-相互并聯(lián)，在靜平衡位置處同時起到支撐作用，使得整個系統(tǒng)具有較高的承載力。P（t）表示設(shè)備產(chǎn)生的激振力，c為隔振系統(tǒng)的阻尼系數(shù)。

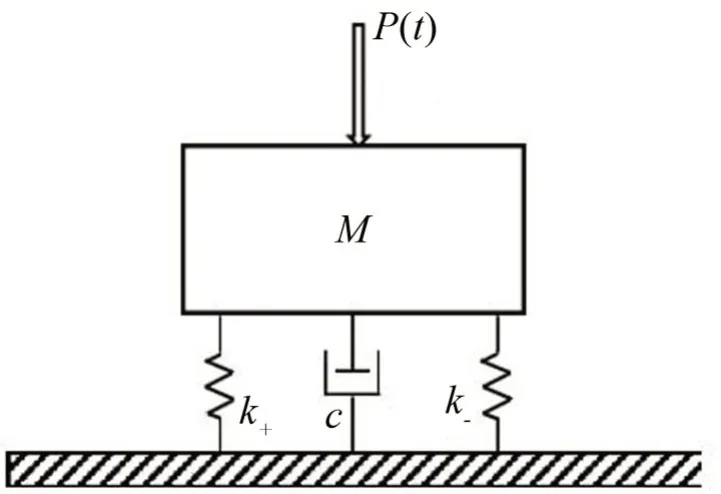
圖5 正負(fù)剛度并聯(lián)隔振系統(tǒng)簡化模型

設(shè)正負(fù)剛度并聯(lián)隔振系統(tǒng)在靜載下的變形為xst，由于隔振系統(tǒng)由碟形彈簧和矩形彈簧共同承載，則靜力平衡方程為：

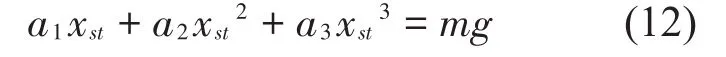
如圖5 所示，對正負(fù)剛度并聯(lián)隔振系統(tǒng)進(jìn)行受力分析，建立隔振系統(tǒng)的運動微分方程：

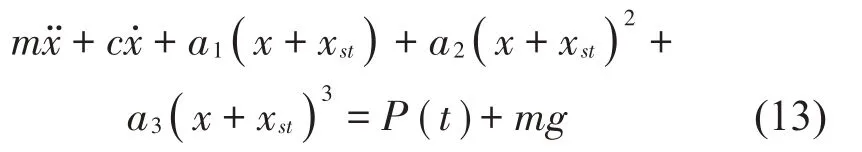
其中：P（t）為隔振系統(tǒng)受到的簡諧激勵力：

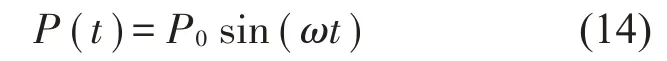
對微分方程式（14）進(jìn)行簡化計算得：

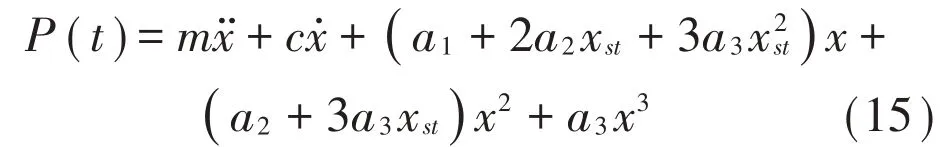
正負(fù)剛度并聯(lián)隔振系統(tǒng)在簡諧激振力P（t）的作用下，其響應(yīng)頻譜中高次諧波位移與基頻諧波位移之比一般小于1%，故設(shè)隔振系統(tǒng)的變形為：

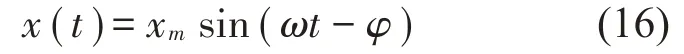
由式（16）可以得到變形速度（t）、加速度（t）：

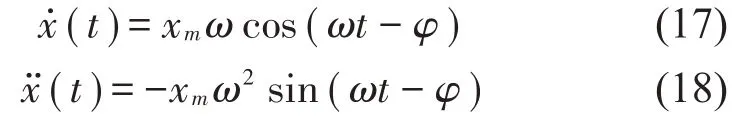
將變形速度（t）、加速度（t）的具體表達(dá)式式（17）、式（18）代入系統(tǒng)運動微分方程式（15）。根據(jù)諧波平衡法，sin（ωt-φ）、cos（ωt-φ）項前的系數(shù)相等（一次諧波平衡，忽略直流項及高次諧波），可得到以下非線性方程組：

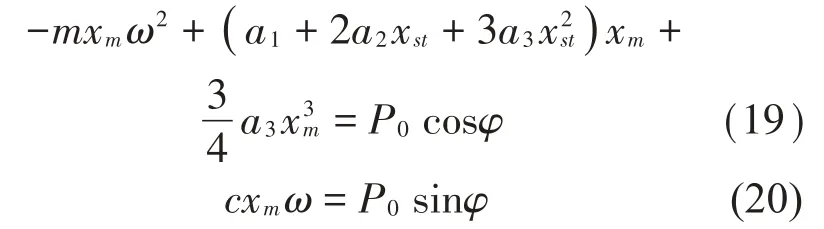
根據(jù)三角關(guān)系式：

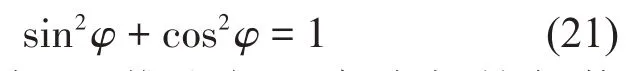
可由式（19）、式（20）推出如下高次超越代數(shù)方程：

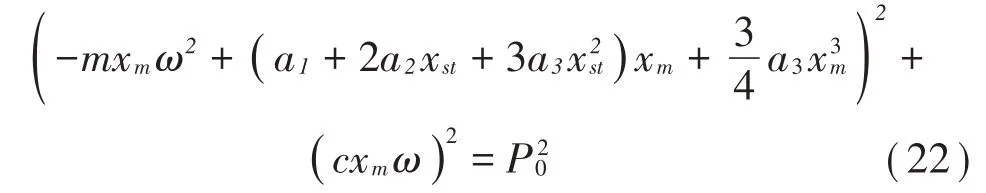
滯后相角φ的表達(dá)式為：

用Newton迭代法求解式（22）可得xm，然后根據(jù)式（23）計算滯后相角，即可得系統(tǒng)在簡諧力激勵下的穩(wěn)態(tài)周期響應(yīng)。

2.3 隔振系統(tǒng)力傳遞率

令Pf(x,,t)表示傳遞到基礎(chǔ)的力，其為彈簧力和阻尼力之和：

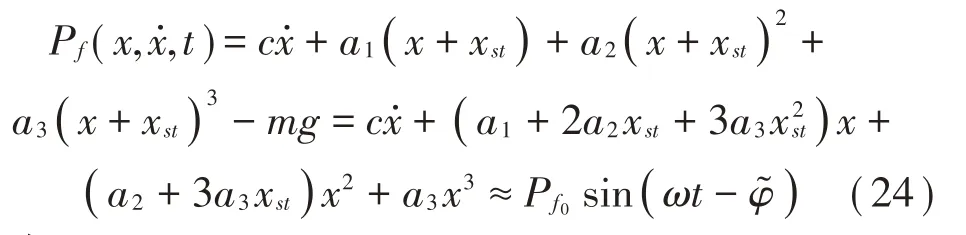
其中：

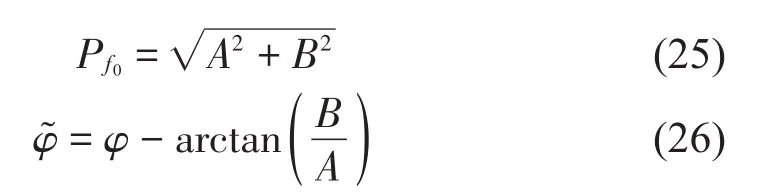
式中：

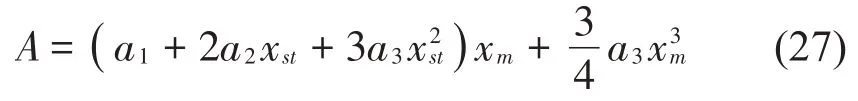
則正負(fù)剛度并聯(lián)隔振系統(tǒng)簡諧力激勵時對基礎(chǔ)的力傳遞率：

3 模型求解與分析

3.1 數(shù)值求解

隔振系統(tǒng)的載荷質(zhì)量為m=400 kg，正負(fù)剛度并聯(lián)機(jī)構(gòu)的等效彈簧力參數(shù)如表1 所示，臨界阻尼系數(shù)：

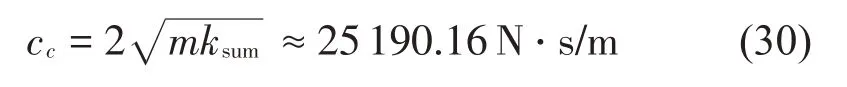
式中：ksum為并聯(lián)機(jī)構(gòu)的剛度（由圖4 可知，在額定載荷時為396 590 N/m）。阻尼比計算公式為：

本文選取低剛度金屬橡膠作為阻尼元件，其阻尼比常介于0.05～0.15 之間，選取阻尼比為0.15，由式（31）可得阻尼系數(shù)為c=3778 N·s/m，選取外部掃頻激勵P=100 sin（ ωt）作為外界激勵（0.1 Hz～200 Hz），通過式（29）可求得外部掃頻激勵下力傳遞率的頻響曲線。

如圖6所示，由數(shù)值求解的結(jié)果可知，該正負(fù)剛度并聯(lián)隔振系統(tǒng)在5.3 Hz 時產(chǎn)生共振，隔振起始頻率為7.5 Hz，表明該隔振系統(tǒng)具有較優(yōu)的低頻隔振性能。

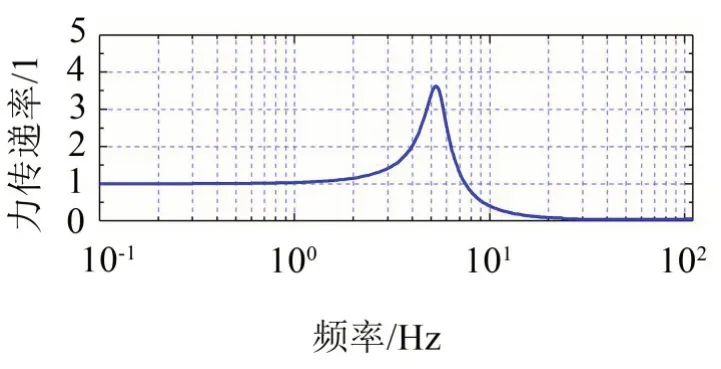
圖6 外部正弦掃頻激勵時隔振系統(tǒng)的力傳遞率頻響曲線

3.2 仿真求解

為了驗證正負(fù)剛度并聯(lián)機(jī)構(gòu)的隔振效果，建立正負(fù)剛度并聯(lián)結(jié)構(gòu)的動力學(xué)仿真模型，對該系統(tǒng)分別采用正弦掃頻信號和隨機(jī)信號進(jìn)行激勵。仿真條件為：正弦掃頻激勵信號，掃頻幅值為100 N，掃頻范圍0.1 Hz～200 Hz，仿真結(jié)果如圖7所示；

圖7（a）為外部掃頻激勵的時域信號P0，圖7（b）為外部掃頻激勵傳遞至基礎(chǔ)的載荷的時域信號Pf0，圖7（c）為外部掃頻激勵時力傳遞率的頻域信號。由仿真結(jié)果可知，在正弦掃頻激勵輸入下，所設(shè)計的正負(fù)剛度并聯(lián)機(jī)構(gòu)的最大共振峰出現(xiàn)在5.3 Hz 左右，隔振起始頻率小于8 Hz。該仿真結(jié)果與理論分析的結(jié)果具有較高的重合度，驗證了理論分析的正確性。

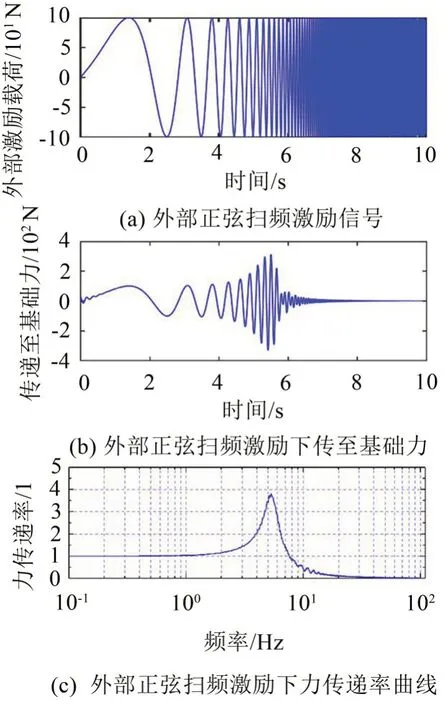
圖7 隔振系統(tǒng)正弦掃頻激勵下的時域響應(yīng)及頻域響應(yīng)

圖8（a）為外部隨機(jī)激勵的時域信號P0，圖8（b）為外部隨機(jī)激勵時傳遞至基礎(chǔ)的載荷的時域信號Pf0，圖8（c）為外部隨機(jī)激勵時力傳遞率的頻響曲線。由仿真實驗可知，正負(fù)剛度并聯(lián)機(jī)構(gòu)的固有頻率較低（5 Hz～6 Hz），隔振起始頻率約為7.2 Hz，因而對于外界的寬頻帶的振動具有良好的隔振效果。隨機(jī)激勵下系統(tǒng)的共振點、隔振起始頻率與數(shù)值計算和正弦掃頻的結(jié)果均具有較高的重合度，進(jìn)一步證明了該剛度并聯(lián)機(jī)構(gòu)具有良好的低頻隔振效果。

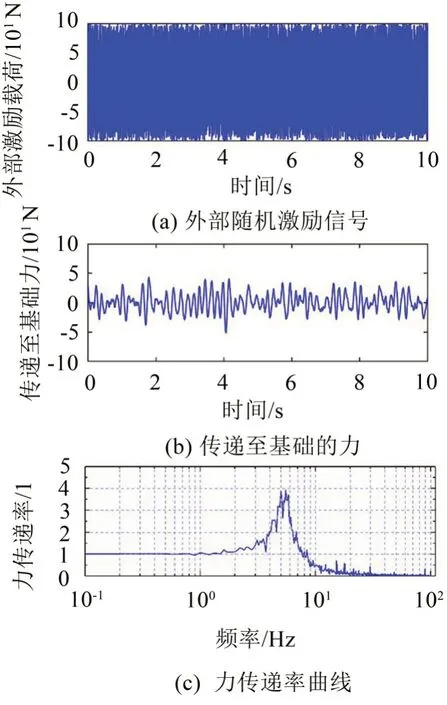
圖8 隔振系統(tǒng)隨機(jī)激勵下的時域響應(yīng)及頻域響應(yīng)

4 力傳遞率性能試驗

為驗證所設(shè)計的隔振系統(tǒng)的實際隔振效果，對隔振系統(tǒng)進(jìn)行力傳遞率試驗。力傳遞率試驗臺架如圖9 所示，本次試驗選用杭州億恒科技有限公司生產(chǎn)的EJZK-50型電磁激振器作為振源，激振器通過激振桿與配重塊剛性連接，激振器與激振桿之間安裝有動態(tài)力傳感器測量輸入的外部擾動力，在隔振器與基礎(chǔ)之間安裝一個動態(tài)力傳感器測量傳遞至基礎(chǔ)的振動水平。

圖9 隔振系統(tǒng)試驗臺架

本文所設(shè)計的隔振系統(tǒng)的額定承載質(zhì)量為400 kg，試驗條件為：由激振器輸出正弦激勵，幅值范圍為70 N～110 N，掃頻范圍5 Hz～200 Hz，掃頻速率1oct/min。

圖10 所示為隔振系統(tǒng)在不同激勵幅值下的力傳遞率曲線，由力傳遞率曲線可知該隔振系統(tǒng)在100 N 的正弦激勵下其1 階共振頻率約為5.4 Hz，這與前文數(shù)值解和仿真解的5.3 Hz 基本吻合；出現(xiàn)的誤差是由試驗儀器的誤差以及阻尼元件的實際阻尼系數(shù)跟理論給定的阻尼系數(shù)有所差異引起的。

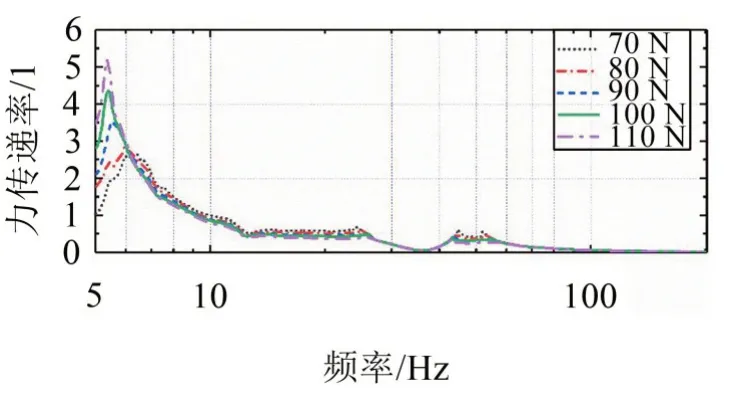
圖10 隔振系統(tǒng)力傳遞率響應(yīng)曲線

由試驗結(jié)果可知，隨著外界激勵幅值逐漸增大，隔振系統(tǒng)的1 階共振頻率逐漸降低，峰值力傳遞率逐漸增大，說明該隔振系統(tǒng)在重載工況下（400 kg）具有較好的低頻隔振能力。

5 結(jié)語

本文將正剛度矩形彈簧和負(fù)剛度碟簧相互并聯(lián)，研制了一種重載低頻被動隔振系統(tǒng)，并構(gòu)建了隔振系統(tǒng)的動力學(xué)模型，得到其數(shù)值解和仿真解，并搭建其力傳遞率試驗臺架，通過掃頻試驗驗證隔振系統(tǒng)的隔振性能。主要結(jié)論如下：

（1）對建立的動力學(xué)模型進(jìn)行簡化數(shù)值求解得到隔振系統(tǒng)的力傳遞率曲線，隔振系統(tǒng)的共振頻率約為5.3 Hz，說明該隔振系統(tǒng)具有較低的固有頻率。

（2）對低頻被動隔振系統(tǒng)進(jìn)行仿真分析，得到其在掃頻激勵和隨機(jī)激勵下的力傳遞率曲線，兩種激勵下隔振系統(tǒng)的共振頻率都在5 Hz～6 Hz 之間，跟數(shù)值計算結(jié)果重合度較高，表明該分析方法的有效性。

（3）不同激勵幅值的掃頻試驗所得到低頻被動隔振系統(tǒng)的1 階共振頻率為5 Hz～6 Hz，在不同激勵幅值下隔振系統(tǒng)均具有較低的固有頻率和較寬的隔振頻帶，進(jìn)一步驗證了所設(shè)計的隔振系統(tǒng)的低頻隔振性能。