考慮軸承故障高速列車齒輪傳動系統振動響應分析

張阿中，劉建新，蔡久鳳

（1.西南交通大學牽引動力國家重點實驗室，成都 610031；2.西南交通大學機械工程學院，成都 610031）

齒輪傳動系統作為鐵路車輛轉向架上的核心傳動部件，其可靠性對列車運行平穩性和安全性有著直接的影響。目前，國內外學者對齒輪傳動系統做了各方面的研究。Fernández 等[1]建立了球軸承支撐的考慮齒廓偏差的齒輪傳動系統動力學模型，并通過實例驗證了該動力學模型的有效性；Gu 等[2]建立了行星齒輪傳動系統的動力學模型，模擬了齒輪出現偏心的故障情況，研究了齒輪偏心對行星齒輪傳動系統動力學行為的影響；陳裴等[3]對行星齒輪傳動系統進行動力學仿真，考慮太陽輪的斷齒故障，研究了齒輪故障后系統的動力學響應。上述文獻在建立齒輪傳動系統動力學模型過程中，均沒有考慮對齒輪傳動系統中的軸承進行精細化建模，同樣也缺少對軸承常見故障的模擬。

近年來，對故障軸承的仿真分析日益增多，劉永強等[4]建立了外圈故障的高速列車軸箱軸承動力學模型，對比分析了正常軸承和故障軸承的動力學行為；吳冬等[5]提出滾動軸承仿真建模方法，建立了鐵路貨車軸承的動力學模型，并驗證了故障軸承模型的合理性；李長健等[6]建立了高速機車雙列圓錐滾子軸承動力學模型，研究了內圈故障狀態下軸承的動力學行為。這些文獻模擬了軌道車輛軸承的常見故障，但只對軸承這一部件單獨進行研究，并沒有考慮軸承和其他部件的相互作用。

對于高速列車的齒輪傳動系統，其輸入軸上的軸承長期處于高速運行的狀況，一旦出現故障，就可能會對整個傳動系統甚至整輛車的穩定運行產生影響。因此，有必要考慮傳動系統中軸承的常見故障，并對其產生的影響進行研究分析。本文在前人研究的基礎上，對高速列車齒輪傳動系統進行精細化建模，同時模擬軸承故障，建立考慮軸承故障的高速列車齒輪傳動系統動力學模型，考慮故障軸承和其他部件的相互作用，研究輸入軸上右側圓柱滾子軸承出現剝離故障時系統的振動響應。

1 齒輪傳動系統動力學模型

本文以國內某高速列車齒輪傳動系統為研究對象，該系統由一對嚙合的斜齒輪、兩個圓柱滾子軸承NU-215、一個深溝球軸承QJ-214、兩個圓錐滾子軸承EC-32994 組成，如圖1 所示。主動齒輪和從動齒輪的齒數分別為35、85。各軸承的結構參數可根據其型號獲得，如表1所示。

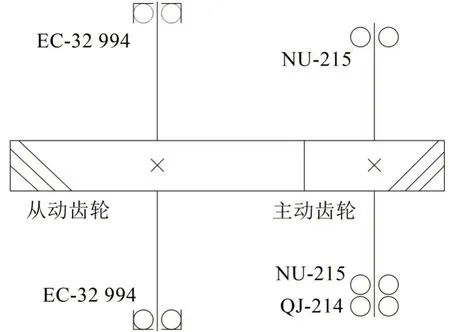
圖1 高速列車齒輪傳動系統簡圖

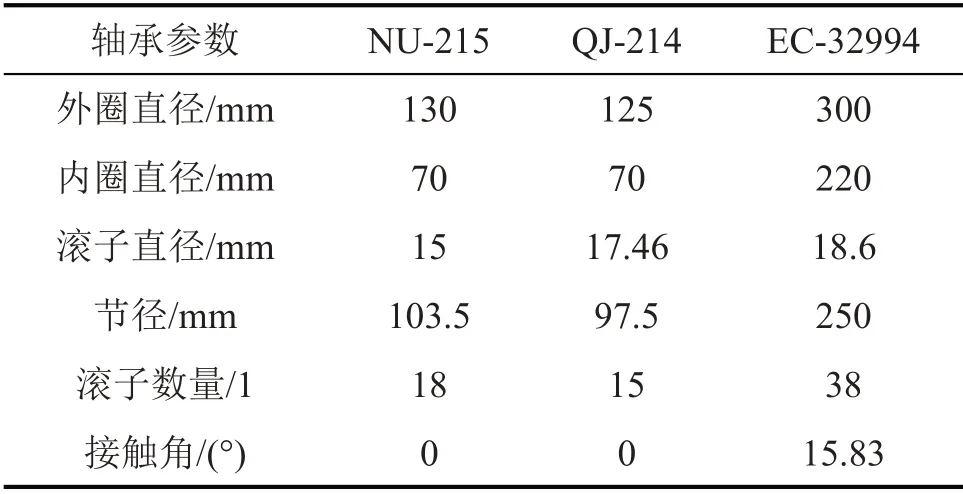
表1 高速列車齒輪傳動系統中個軸承的結構參數

故障工況下，輸入軸上右側圓柱滾子軸承的內圈滾道上出現剝離故障，故障內圈是在正常內圈的基礎上，切除截面為6 mm×1.5 mm的矩形凹槽來模擬，故障內圈的幾何模型如圖2（a）所示。

在SolidWorks 中創建好各零部件的幾何模型后，導入到RecurDyn中進行傳動系統動力學模型的創建，建模過程中，不考慮各部件的彈性變形。

1.1 接觸關系設置

齒輪傳動系統中需要設置接觸的元件較多，滾動軸承需要設置滾子與內外圈、保持架之間的接觸；主動齒輪和從動齒輪需在齒面上設置接觸。Recur-Dyn 中計算法向接觸力的方法為罰函數法，它將接觸非線性問題轉化為材料非線性問題。基于Hertz接觸理論，接觸過程中，法向接觸力fn的計算公式為[7-8]：

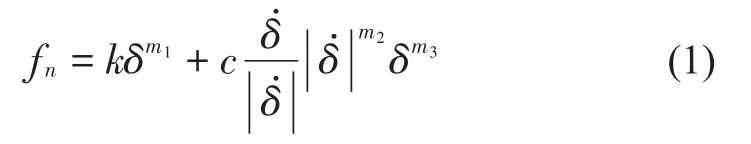
式中：k為接觸剛度系數；c為阻尼系數；δ為接觸穿透深度；為接觸點的相對速度；m1、m2、m3分別為剛度指數、阻尼指數、凹痕指數。

1.2 約束設置

為模擬高速列車齒輪傳動系統的實際運行狀況，將所有軸承的外圈與大地固定，輸入軸上軸承的內圈、主動齒輪與輸入軸固定，輸出軸上軸承的內圈、從動齒輪與輸出軸固定，并在輸入軸上添加驅動，角速度函數設置為STEP（TⅠME，0，0，0.2，440）。高速列車齒輪傳動系統的動力學模型如圖2（b）所示。

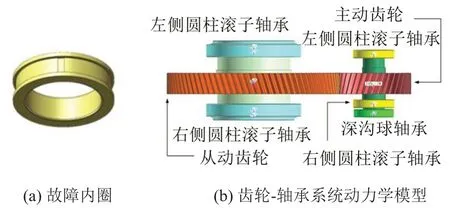
圖2 齒輪傳動系統動力學模型

2 模型驗證

2.1 理論基礎

滾動軸承正常運行時，假設滾子在內外圈滾道上的滾動為純滾動，且軸承內外圈角速度保持不變，則保持架以及滾子的角速度[9]分別為：

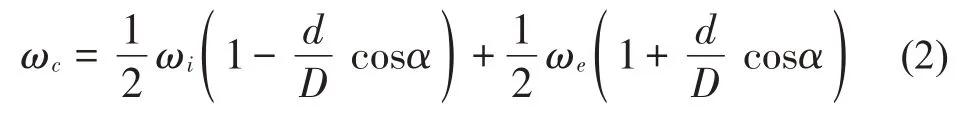
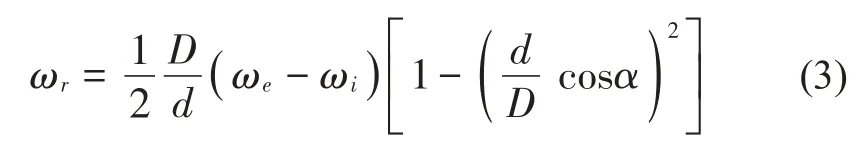
式中：ωc為保持架角速度，rad/s；ωr為滾子自轉角速度，rad/s；ωi為內圈角速度，rad/s；ωe為外圈角速度，rad/s；d為滾子直徑，mm；D為軸承節徑，mm；α為接觸角。

當滾動軸承中的零部件出現故障時，在軸承轉動過程中，故障部位會與其他零件碰撞，從而產生一定頻率的周期性激勵，引起整個滾動軸承的振動。

滾動軸承內圈故障特征頻率[10]計算公式為：

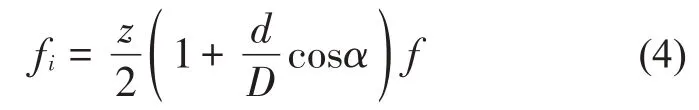
式中：fi為內圈故障特征頻率，Hz；z為滾子個數；f為軸承內圈的轉動頻率，Hz。

齒輪的嚙合頻率的計算公式為：

式中：fm為齒輪嚙合頻率，Hz；fs為主動齒輪轉頻，Hz；zs為主動齒輪齒數。

2.2 模型驗證

通過仿真可得到齒輪傳動系統中各零部件的轉速，將RecurDyn中得到的軸承保持架和滾子角速度仿真值與公式（2）～公式（3）計算出的理論值比較，如表2所示。

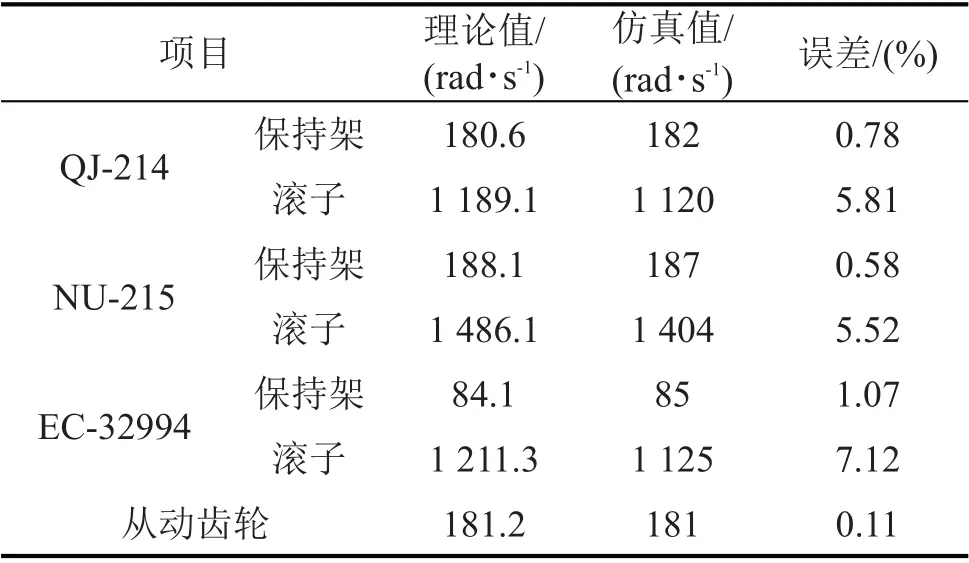
表2 理論結果與仿真結果比較

從表2中可以看出，輸出軸上圓錐滾子軸承EC-32994的滾子角速度誤差最大，考慮到軸承運轉過程中滾子不可能一直做純滾動，以及建模時對模型的簡化，同時軟件自身也存在一定的求解誤差，且上述誤差值均小于10%，處在合理范圍內，可以驗證齒輪傳動系統動力學模型在運動學方面的合理性。

3 仿真計算

通過仿真分析，比較正常工況與故障工況下，齒輪傳動系統中各零部件的振動響應，討論軸承故障對系統的影響。

3.1 齒輪傳動系統轉速分析

在驗證模型合理性的基礎上，比較正常工況與故障工況下齒輪傳動系統各零部件的角速度。從動齒輪的角速度如圖3所示，從圖中可以看出：正常工況下從動齒輪的角速度約為181 rad/s，與理論計算的結果很接近，且幾乎沒有波動；故障工況下從動齒輪的角速度有較大的波動，齒輪傳動的穩定性降低。

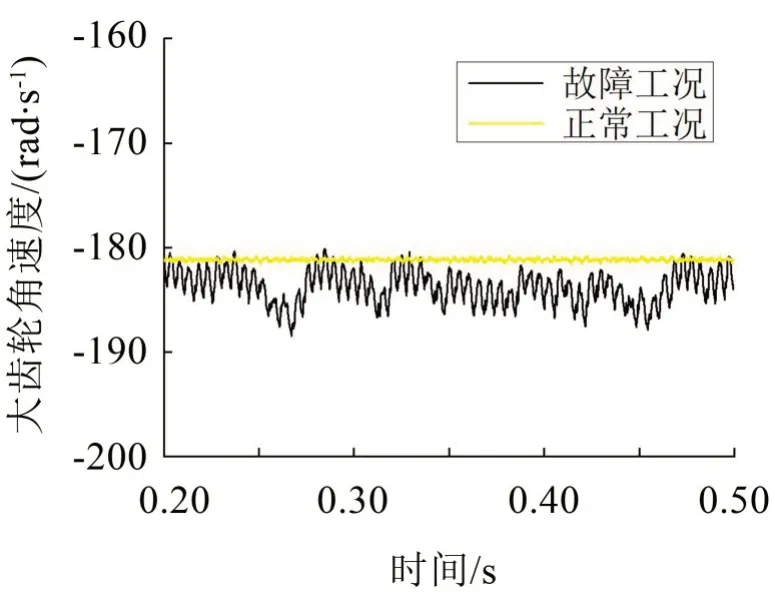
圖3 從動齒輪角速度

輸出軸上圓錐滾子軸承滾子的角速度如圖4所示，從圖中可以看出：故障工況下滾子的角速度比正常工況下有所增大，但并不明顯，說明輸入軸上的軸承出現故障對輸出軸上的軸承影響較小。

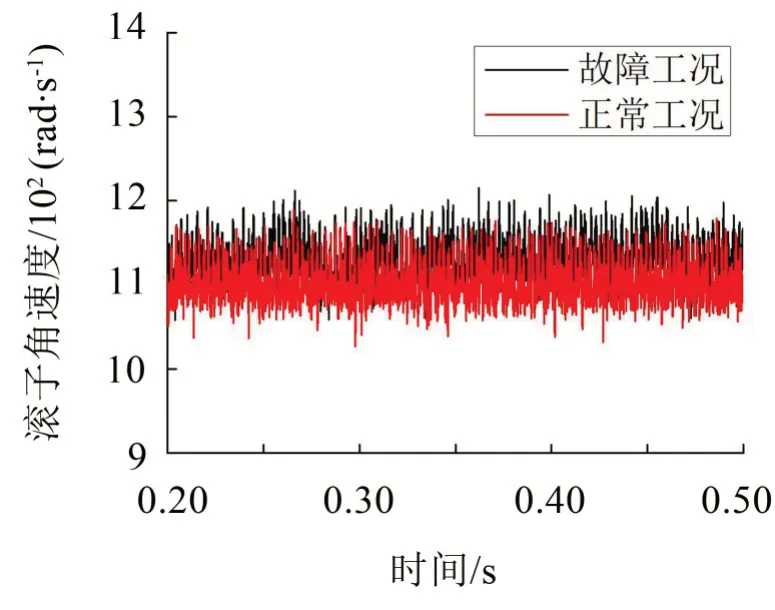
圖4 圓錐滾子軸承滾子角速度

輸入軸上右側圓柱滾子軸承角速度如圖5（a）所示，從圖中可以看出：故障工況與正常工況下滾子角速度均值相差不大，但故障工況下滾子的角速度發生周期性突變，突變出現的時間間隔約為0.025 s，頻率為40 Hz，為內圈轉動頻率70.03 Hz與保持架轉動頻率29.76 Hz（即滾子公轉頻率）之差，這是因為滾子公轉方向與內圈轉動方向相同，滾子無需公轉一圈就會與內圈的故障部位發生碰撞，導致角速度突變。

輸入軸上左側圓柱滾子軸承滾子的角速度如圖5（b）所示，從圖中可以看出：故障工況與正常工況下滾子角速度的均值相差較小，但故障工況下，滾子角速度發生突變，且呈現一定的周期性。由此可見，輸入軸上右側圓柱滾子軸承故障不僅會使自身滾子的角速度突變，還會影響到同一軸上的其他軸承，使其角速度也發生突變。

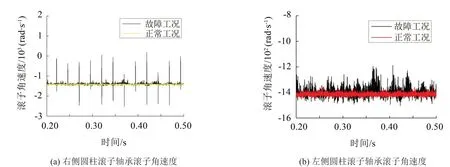
圖5 圓柱滾子軸承滾子角速度

3.2 齒輪傳動系統振動分析

由于主動齒輪、圓柱滾子軸承和深溝球軸承的內圈均固定在輸入軸上，從動齒輪與圓錐滾子軸承內圈固定在輸出軸上，對于多剛體系統而言，同一軸上各零件的振動加速度相同，因此只討論主動齒輪和從動齒輪振動加速度的變化情況。

主動齒輪的振動加速度如圖6（a）所示，經計算，正常工況下主動齒輪加速度的均方根值為873.03 m/s2，故障工況下為1 587.02 m/s2，由此可見，輸入軸上的軸承出現故障后，會使主動齒輪的加速度明顯增大。主動齒輪的振動加速度如圖6（b）所示，經計算正常工況下主動齒輪加速度的均方根值為63.69 m/s2，故障工況下為232.29 m/s2，由此可見，輸入軸上的軸承出現故障后，同樣也會使從動齒輪的加速度增大。

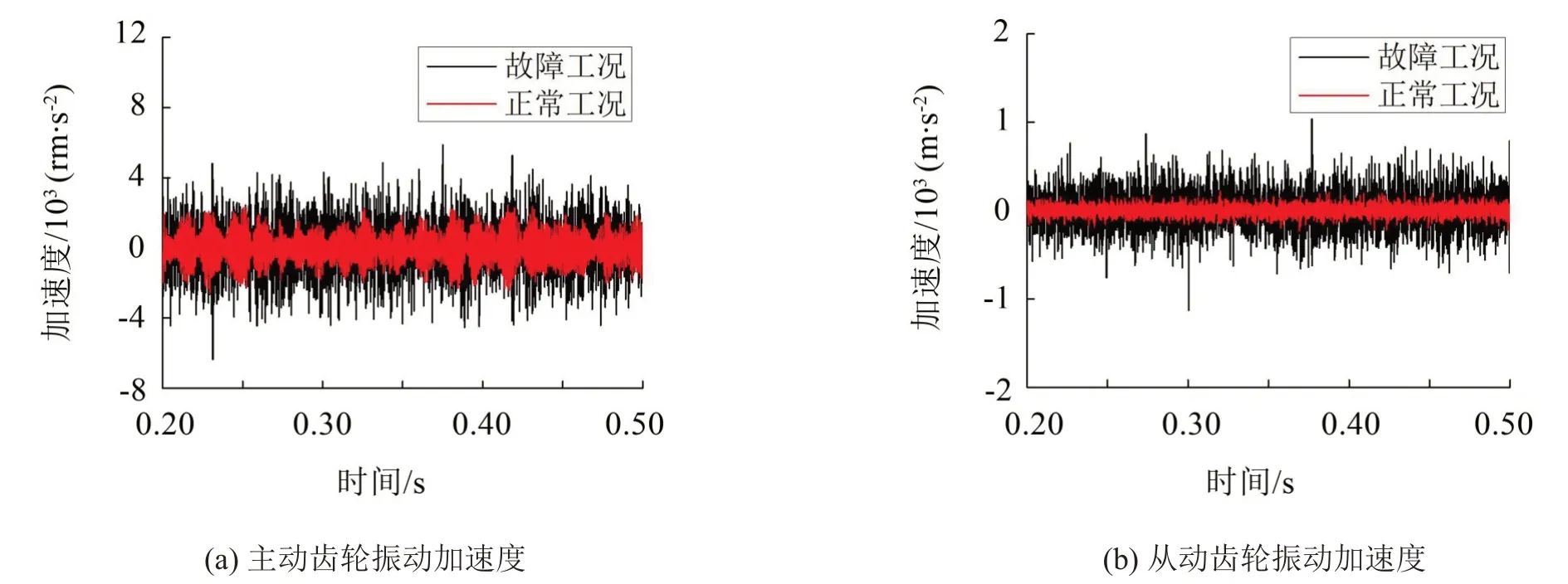
圖6 齒輪振動加速度

根據公式（4）～公式（5），可求得圓柱滾子軸承內圈故障特征頻率721 Hz，齒輪的嚙合頻率為2 451 Hz。

對故障工況下主動齒輪和從動齒輪的振動加速度進行譜分析，得到的加速度頻譜圖如圖7（a）～圖7（b）所示。可以發現：故障工況下，在圖7（a）中，主動齒輪加速度頻譜圖在723.82 Hz處出現峰值，與理論計算的圓柱滾子軸承NU-215 內圈故障特征頻率非常接近，在1 449.65 Hz 處也出現峰值，為內圈故障頻率的2倍頻，同時，在圖中還可發現內圈故障頻率的2 倍頻與主動齒輪轉頻70.03 Hz 的調制頻率1 519.63 Hz 和1 377.66 Hz；頻譜圖中1 421.65 Hz 處出現峰值，為內圈故障頻率的2 倍頻與圓柱滾子軸承保持架轉頻29.76 Hz 的調制頻率；頻譜圖中2 451.40 Hz 處出現峰值，與理論計算得到的齒輪嚙合頻率很接近，在圖中還可發現齒輪嚙合頻率與主動齒輪轉頻3倍頻的調制頻率2 241.45 Hz。

如圖7（b）所示，故障工況下，從動齒輪的加速度頻譜圖中也出現圓柱滾子軸承內圈故障頻率723.83Hz 及其2 倍頻1 449.65 Hz，頻譜圖中還可發現齒輪嚙合頻率2 451.40 Hz。

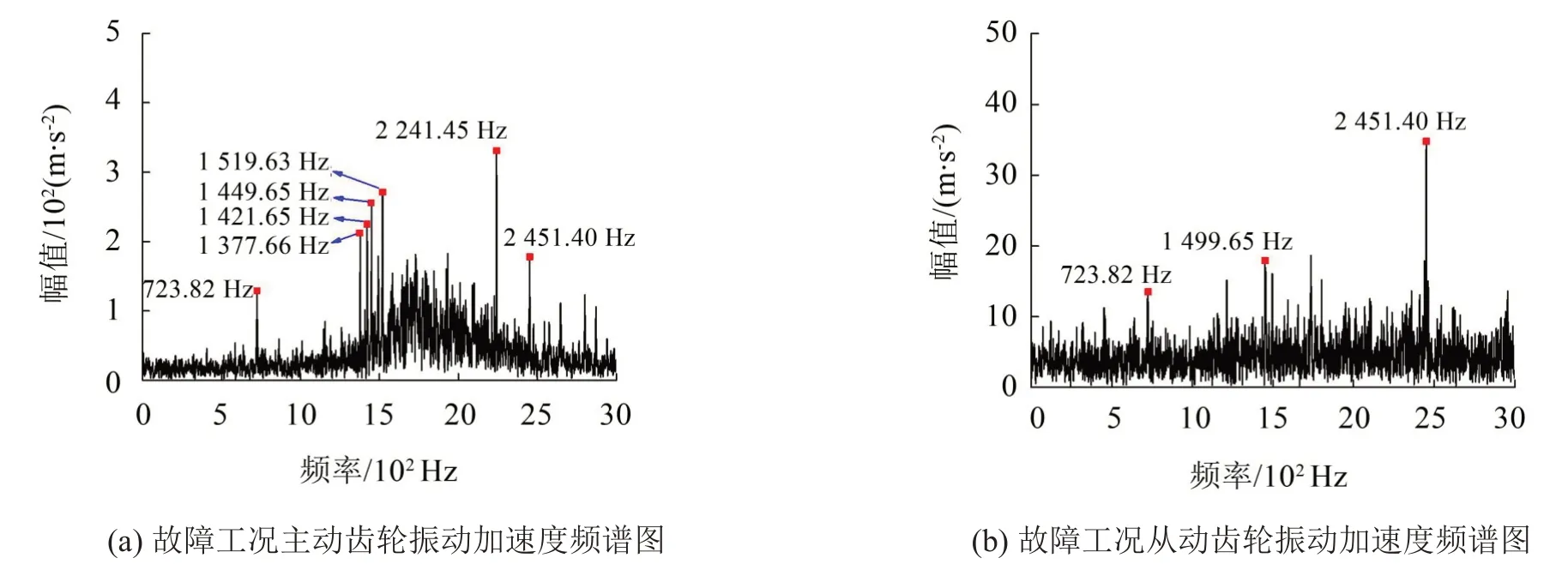
圖7 齒輪加速度頻譜圖

通過上述分析，可以驗證故障工況下齒輪傳動系統動力學模型的合理性。

3.3 齒輪傳動系統接觸力分析

通過仿真分析得到主動齒輪和從動齒輪的接觸力如圖8所示。

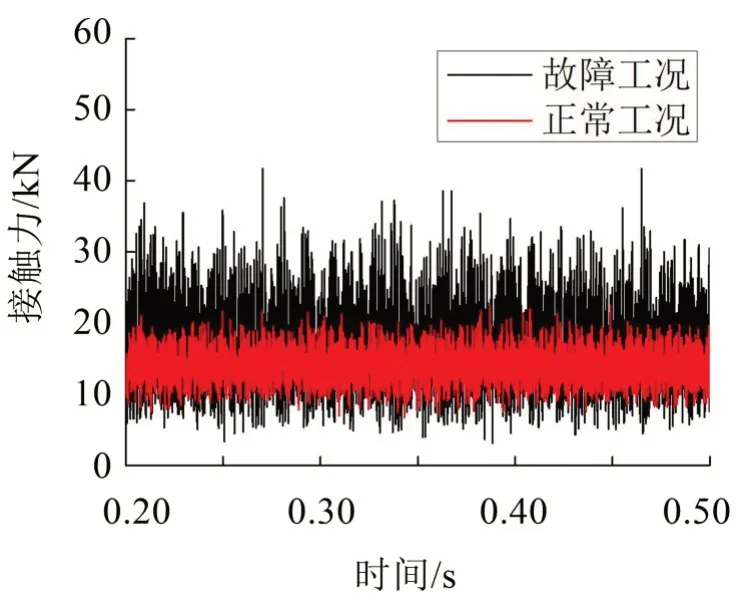
圖8 齒輪齒面接觸力

從圖中可以看出，正常工況下，齒輪的接觸力約為1 500 N，波動較小；故障工況下，齒輪的接觸力急劇增大，由此可見，輸入軸上右側圓柱滾子軸承故障會導致齒輪齒面間的接觸情況變得惡劣，進而可能縮短齒輪的使用壽命。

深溝球軸承滾子與內圈的接觸力如圖9 所示，從圖中可以看出，故障工況下，接觸力出現較大的波動，在某些時刻增大，在某些時刻又會減小到0，這是因為受到右側圓柱滾子軸承剝離故障的影響，同一輸入軸上深溝球軸承的滾子與內圈之間碰撞加劇，在某些時刻，接觸力增大，同時由于軸承游隙的存在，滾子與內圈在某些時刻不產生接觸，導致接觸力為0，滾子與內圈瞬時脫離。

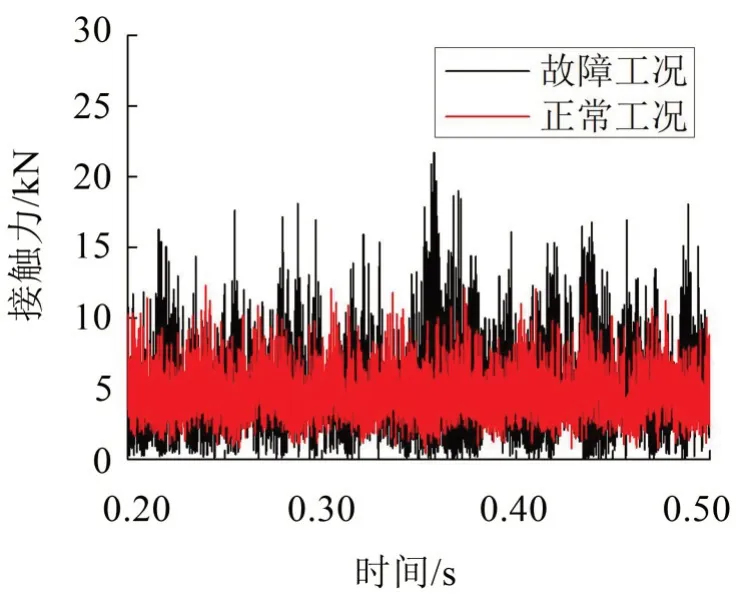
圖9 深溝球軸承滾子與內圈接觸力

右側圓柱滾子軸承滾子與內圈接觸力如圖10（a）所示，從圖中可以看出，與正常工況相比，故障工況下，滾子與內圈之間的接觸力出現較大波動，在某些時刻增加，在某些時刻又會減小到0，說明滾子在經過內圈滾道上的剝離故障時，由于受到沖擊，接觸力會增大，但也因為剝離故障的存在，滾子與內圈在某些時刻不產生接觸，導致接觸力為0，滾子與內圈瞬時脫離。左側圓柱滾子軸承滾子與內圈的接觸力如圖10（b）所示，從圖中可以看出，故障工況下，滾子與內圈之間的接觸力增大，說明左側圓柱滾子軸承受到故障軸承的影響，滾子與內圈之間的碰撞加劇。

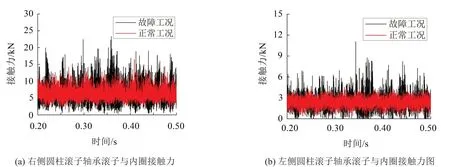
圖10 圓柱滾子軸承滾子與內圈接觸力

4 結語

為研究軸承出現故障后高速列車齒輪傳動系統的振動響應，利用SolidWorks 和Recurdyn 建立了傳動系統的動力學模型，在驗證模型合理的基礎上，對模型進行仿真分析，通過比較正常工況和故障工況下系統的動力學行為，得到以下結論：

（1）高速列車齒輪傳動系統在運行過程中，受到輸入軸上右側圓柱滾子軸承內圈剝離故障的影響，從動齒輪的角速度變化劇烈，齒輪傳動的穩定性降低；輸入軸上各軸承滾子的角速度都會出現周期性突變，而輸出軸上軸承受到的影響較小，滾子的角速度變化不明顯。

（2）高速列車齒輪傳動系統在運行過程中，受到輸入軸上右側圓柱滾子軸承內圈剝離故障的影響，輸入軸上包括從動齒輪在內的所有零部件的振動加速度均明顯增大，輸出軸上所有零件的振動加速度也會增大。

（3）高速列車齒輪傳動系統在運行過程中，故障軸承的滾子與內圈剝離故障處碰撞產生的沖擊會傳遞到齒輪上，導致齒輪齒面間的接觸力急劇增大，齒面接觸情況惡劣，進而會縮短齒輪的使用壽命。

（4）高速列車齒輪傳動系統在運行過程中，故障軸承的滾子與內圈故障處碰撞產生的沖擊會使輸入軸上軸承的滾子與內圈的接觸力出現較大波動，在某些時刻會增大，但由于軸承游隙的存在，滾子與內圈在某些時刻會發生瞬時脫離，導致接觸力減小到0，從而影響系統的穩定運行。

本文關于含故障軸承的齒輪傳動系統動力學模型建模方法具有較高的準確性，該方法不僅僅可用于高速列車的齒輪傳動系統，還適用于多數機械結構的齒輪傳動系統，可以為齒輪傳動系統故障診斷、預防提供參考數據。