輸電線路內(nèi)懸浮抱桿起升動(dòng)載系數(shù)的研究

馬 勇，夏擁軍，孟凡豪，孫立江，安 平，龔 巖

（1.中國(guó)電力科學(xué)研究院有限公司輸變電工程研究所，北京 100055；2.國(guó)網(wǎng)甘肅省電力公司建設(shè)分公司，蘭州 730050）

隨著經(jīng)濟(jì)社會(huì)的發(fā)展，電力行業(yè)在人們的生產(chǎn)生活中發(fā)揮著越來(lái)越重要的作用。2020年我國(guó)成為電力需求量第二大的經(jīng)濟(jì)體，但我國(guó)電力資源地域分布不均勻，往往需要進(jìn)行遠(yuǎn)距離大功率的電力輸送。電力抱桿是一種為了滿足架設(shè)輸電線路需求的格構(gòu)式起重機(jī)械[1-2]，其中懸浮式抱桿因其結(jié)構(gòu)簡(jiǎn)單，使用安裝方便得到了廣泛的應(yīng)用[3-5]。相關(guān)學(xué)者對(duì)電力抱桿的動(dòng)態(tài)特性展開(kāi)了研究。葉立運(yùn)等[6]采用計(jì)算機(jī)輔助技術(shù)對(duì)內(nèi)懸浮外拉線抱桿組立1 000 kV 耐張塔進(jìn)行了分析；張謙等[7]基于非線性有限元方法，對(duì)組塔施工內(nèi)懸浮內(nèi)拉線抱桿結(jié)構(gòu)進(jìn)行了仿真計(jì)算分析；徐金城[8]等人利用ANSYS 仿真軟件對(duì)懸浮抱桿的風(fēng)振響應(yīng)進(jìn)行了分析，發(fā)現(xiàn)抱桿中部振幅最大，安裝過(guò)程中應(yīng)對(duì)加強(qiáng)中部標(biāo)準(zhǔn)節(jié)的連接；趙紅波[9]利用回歸分析，研究了風(fēng)載荷對(duì)懸浮抱桿的影響。現(xiàn)有的懸浮抱桿動(dòng)態(tài)特性相關(guān)研究主要集中在風(fēng)載荷的影響，研究形式主要以有限元仿真為主，而懸浮抱桿對(duì)吊件的起升存在沖擊作用，目前尚未研究，導(dǎo)致內(nèi)懸浮抱桿的使用及計(jì)算選型存在一定安全風(fēng)險(xiǎn)。本文對(duì)懸浮抱桿的起升動(dòng)載系數(shù)進(jìn)行研究，首先建立懸浮抱桿的空間結(jié)構(gòu)動(dòng)力學(xué)模型，利用剛度和位移的關(guān)系求解等效剛度，利用動(dòng)能等效的原理求解等效質(zhì)量，之后根據(jù)等效剛度和等效質(zhì)量的求解結(jié)果得到起升動(dòng)載的表達(dá)式，最后通過(guò)ANSYS有限元仿真驗(yàn)證表達(dá)結(jié)果的正確性。

1 研究對(duì)象的選取

抱桿是特高壓及各電壓等級(jí)電網(wǎng)的重要組塔施工裝備之一，針對(duì)不同的載荷需求、不同的施工環(huán)境，可選擇的抱桿有內(nèi)懸浮抱桿、人字抱桿、落地?fù)u臂抱桿與落地平臂抱桿等。其中，內(nèi)懸浮抱桿因結(jié)構(gòu)簡(jiǎn)單、重量輕、運(yùn)輸方便等優(yōu)點(diǎn)被廣泛應(yīng)用。按照拉線形式，內(nèi)懸浮抱桿分為內(nèi)懸浮外拉線抱桿與內(nèi)懸浮內(nèi)拉線抱桿，分別如圖1（a）與圖1（b）所示。內(nèi)懸浮外拉線抱桿是把抱桿的拉線錨固在地面設(shè)置好的地錨上，抱桿的穩(wěn)定性好，安全性高；內(nèi)懸浮內(nèi)拉線抱桿是把抱桿的拉線錨固在已組好的鐵塔主材上，由于鐵塔為桁架結(jié)構(gòu)，具有一定的彈性，且內(nèi)拉線方式使得抱桿吊裝工作時(shí)傾斜角度小，對(duì)控制繩的要求高，安全性與穩(wěn)定性較差。因此，內(nèi)懸浮外拉線抱桿更具有普遍性，故選取內(nèi)懸浮外拉線抱桿（簡(jiǎn)稱(chēng)懸浮抱桿）作為研究對(duì)象。

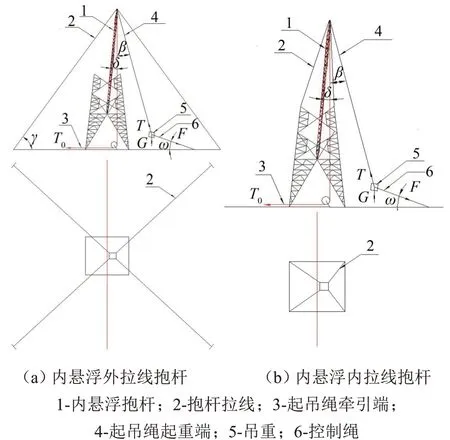
圖1 懸浮抱桿工作示意圖

2 剛度和質(zhì)量的分析

懸浮抱桿未受載時(shí)由抱桿和拉索組成，抱桿的長(zhǎng)度為L(zhǎng)，四根拉索在空間中均勻分布，長(zhǎng)度相等，抱桿和拉索與地面之間全部為鉸接。懸浮抱桿受載時(shí)，其中兩根拉索放松，結(jié)構(gòu)由另外兩根拉索和抱桿組成，如圖2所示。抱桿與空間z軸的夾角為γ，拉索與xOy平面的夾角為α，兩根拉索之間的夾角為2θ，且拉索平面與xOy平面之間的夾角為β。

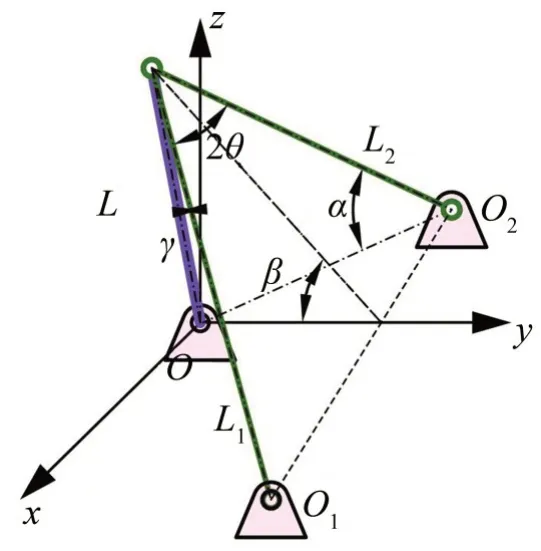
圖2 懸浮抱桿的幾何結(jié)構(gòu)

2.1 剛度的等效

在吊點(diǎn)處施加豎直向下的力F,設(shè)拉索中的張力分別為T(mén)1、T2，抱桿中的軸力為N，懸浮抱桿的受力情況如圖3所示。

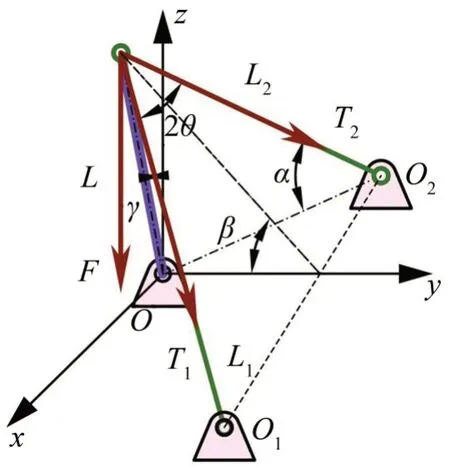
圖3 懸浮抱桿的受力情況

在拉索平面內(nèi)對(duì)拉索的張力進(jìn)行合成，如圖4（a）所示，拉索張力的合力為T(mén)=2T1cosθ。在yOz平面內(nèi)進(jìn)行力的分解，如圖4（b）所示。

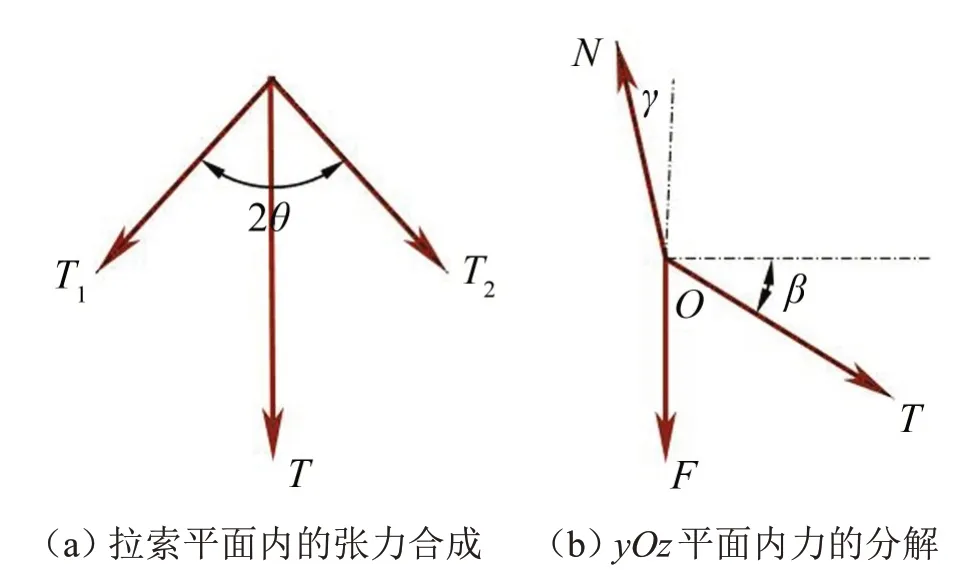
圖4 懸浮抱桿受力分析

根據(jù)力的平衡條件∑F=0，得到懸浮抱桿的靜力學(xué)平衡方程如式（1）所示。

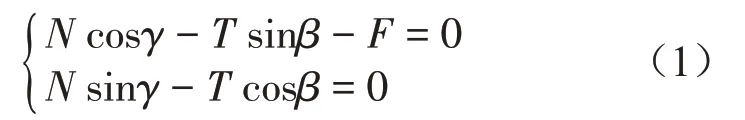
求解方程組，求解結(jié)果如式（2）所示。

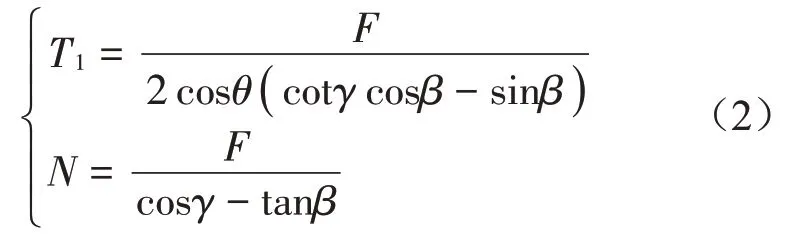
設(shè)單側(cè)拉索的橫截面積為A1，彈性模量為E，起重臂的橫截面積為A，彈性模量為E。根據(jù)結(jié)構(gòu)力學(xué)的相關(guān)知識(shí)，吊點(diǎn)處受力后的位移如式（3）所示。

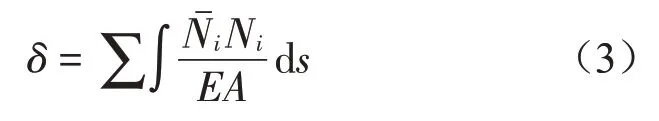
代入相關(guān)數(shù)值，得到懸浮抱桿在F作用下吊點(diǎn)處的位移如式（4）所示。

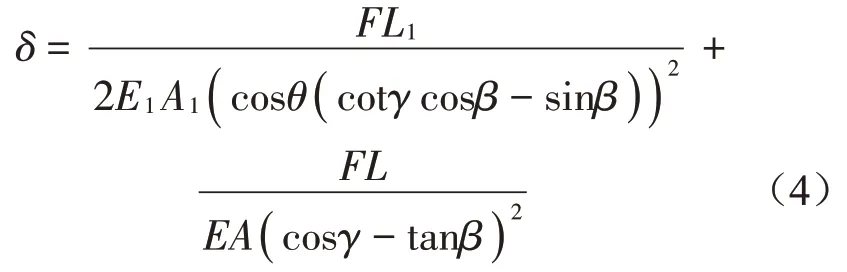
2.2 質(zhì)量的等效

假設(shè)懸浮抱桿受載后結(jié)構(gòu)發(fā)生微小變形，角度變化Δγ，則抱桿與xOy平面的夾角為γ+Δγ。根據(jù)圖2 可知，懸浮抱桿各個(gè)單元體的絕對(duì)位置矩陣分別如式（5）至式（7）所示。

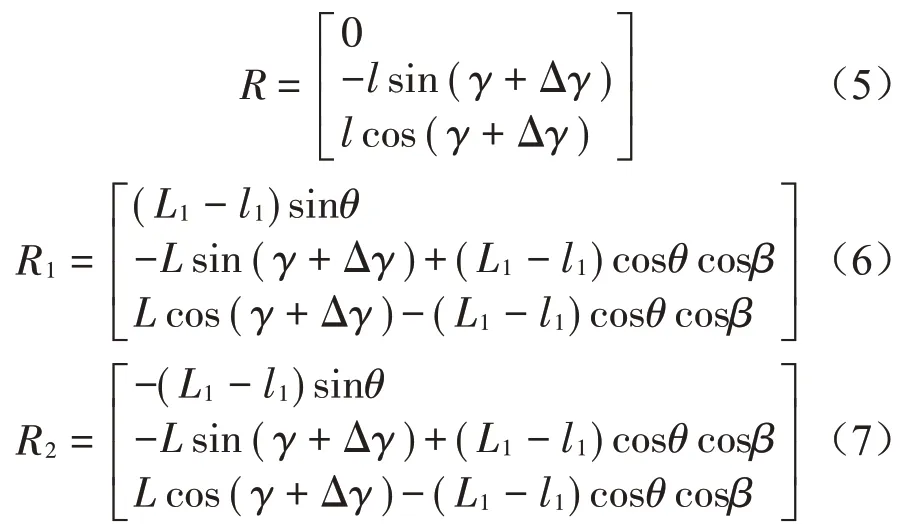
各個(gè)單元體相對(duì)位置與絕對(duì)位置的關(guān)系如式（8）所示。

當(dāng)Δγ→0 時(shí)，cosΔγ≈1，sinΔγ=，各個(gè)單元體絕對(duì)位移矩陣與位置矩陣的關(guān)系如式（9）所示。

單元體相對(duì)位移矩陣與絕對(duì)位移矩陣的關(guān)系如式（10）所示。根據(jù)式（5）至式（10），各個(gè)單元體的相對(duì)位移矩陣如式（11）至式（12）所示。

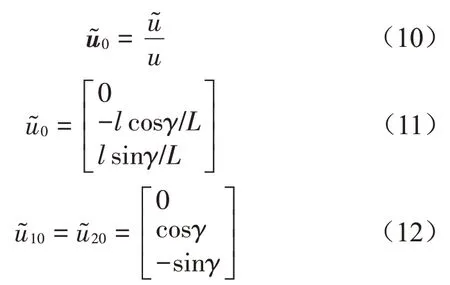
懸浮抱桿等效質(zhì)量如式（13）所示。

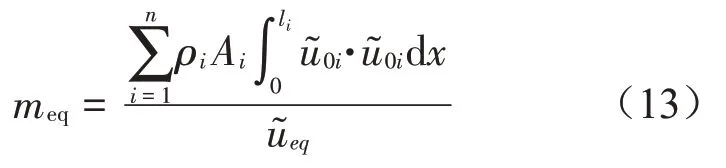
懸浮抱桿的吊點(diǎn)位于拉索和起重臂的鉸接點(diǎn)，因此等效相對(duì)位移，懸浮抱桿的等效質(zhì)量如式（14）所示。

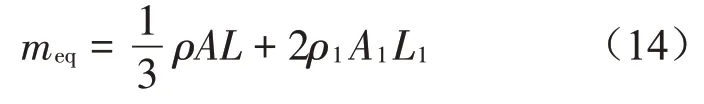
3 起升動(dòng)載系數(shù)的表達(dá)與驗(yàn)證

3.1 動(dòng)載系數(shù)的表達(dá)

建立懸浮抱桿起升動(dòng)力學(xué)模型，進(jìn)行求解，起升動(dòng)載系數(shù)的表達(dá)式如式（15）所示。

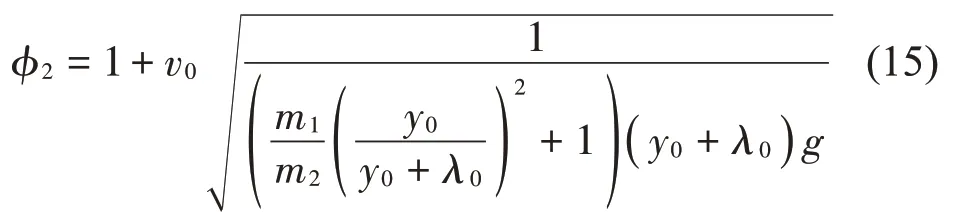
在實(shí)際工程問(wèn)題中，鋼絲繩的剛度和結(jié)構(gòu)位移不易直接求得。設(shè)與載荷相連的鋼絲繩的彈性模量為EQ，長(zhǎng)度為L(zhǎng)Q，單根鋼絲繩的截面積為A0，鋼絲繩的倍率為a，則鋼絲繩的剛度可以表示為，因此，懸浮抱桿的起升動(dòng)載系數(shù)可以用式（16）表示。其中，鋼絲繩的彈性模量可根據(jù)GB/T 24191-2009《鋼絲繩實(shí)際彈性模量測(cè)定方法》測(cè)量得到，對(duì)于重要的鋼絲繩，可要求鋼絲繩生產(chǎn)廠家提供。

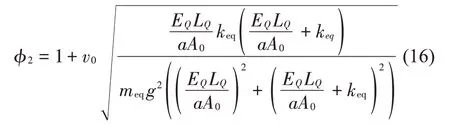
3.2 有限元仿真驗(yàn)證

選擇□800型懸浮抱桿進(jìn)行有限元驗(yàn)證。□800型懸浮抱桿長(zhǎng)度為43.4 m，標(biāo)準(zhǔn)節(jié)外徑寬800 mm，主弦采用了∟100×8 角鋼，斜腹桿采用∟56×5 角鋼。拉索鋼絲繩和起升鋼絲繩均選單倍率?15.5 6×19交繞型纖維芯鋼絲繩。初始狀態(tài)拉索與地面之間的夾角α=45°，起升載荷時(shí)抱桿與豎直方向的最大夾角γmax=10°。

由式（4）、式（15）及式（16）可得□800 型懸浮抱桿的等效剛度為2.06×104N/m，等效質(zhì)量為1.53×103kg，起升動(dòng)載系數(shù)的表達(dá)式為?2=1+0.265v0。

利用ANSYS建立懸浮抱桿的有限元模型，在拉索與地面連接處施加全約束，在抱桿根部施加鉸接約束，在吊點(diǎn)處施加靜載10 kN，懸浮抱桿的位移如圖5所示，□800型懸浮抱桿的靜位移為0.028 9 m。

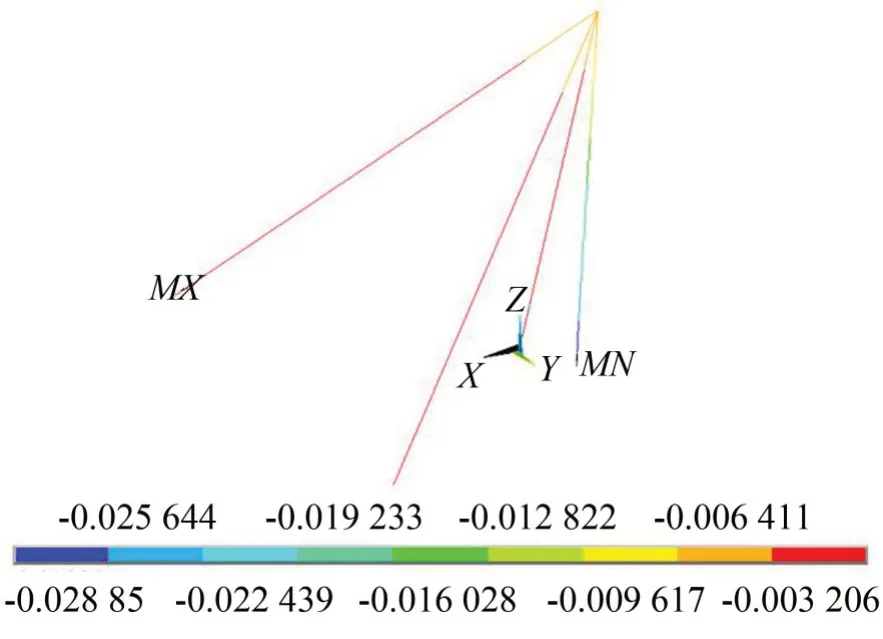
圖5 50 kN靜態(tài)載荷下懸浮抱桿的位移情況

對(duì)懸浮抱桿分別施加不同的外力，使其以不同的起升速度進(jìn)行起升，使用ANSYS進(jìn)行瞬態(tài)動(dòng)力學(xué)分析，吊點(diǎn)處位移隨時(shí)間的變化如圖6所示。

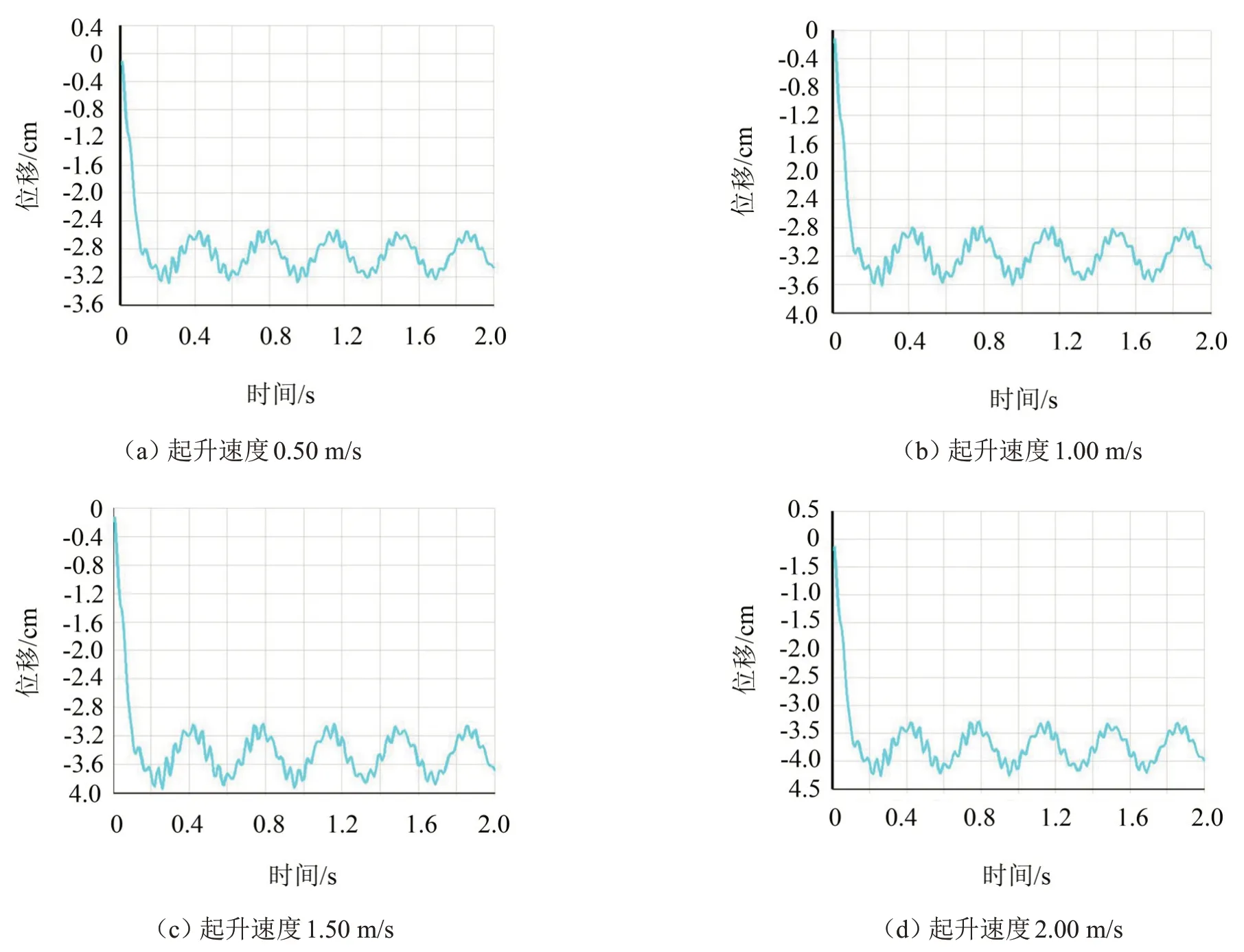
圖6 不同起升速度吊點(diǎn)位移隨時(shí)間變化

將不同起升速度下吊點(diǎn)最大位移的有限元仿真結(jié)果進(jìn)行整理，如表1所示；將理論值與仿真值進(jìn)行比較，如圖7所示。

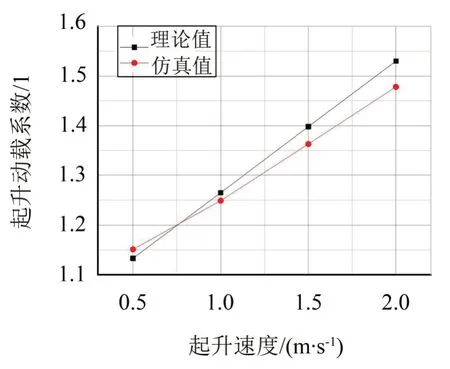
圖7 起升動(dòng)載系數(shù)理論值與仿真值比較

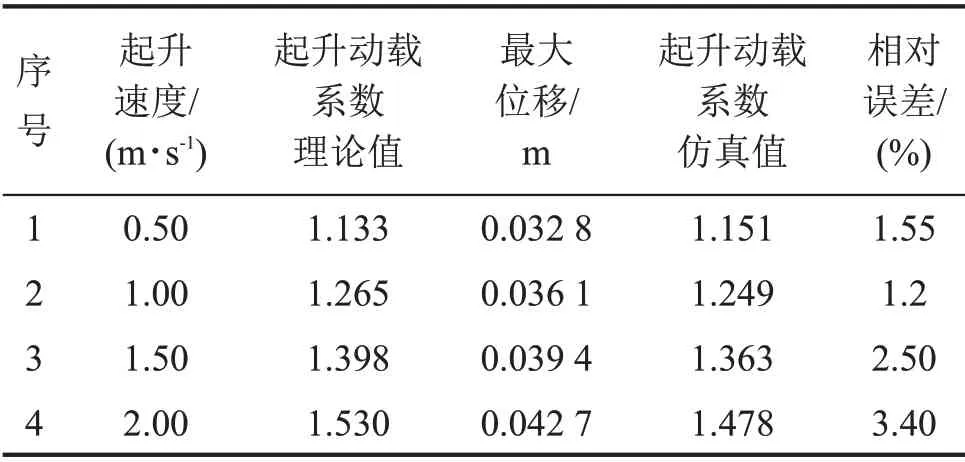
表1 不同起升速度起升動(dòng)載系數(shù)仿真結(jié)果

由有限元仿真結(jié)果可知，對(duì)于□800 型懸浮抱桿，起升動(dòng)載系數(shù)的理論值與仿真值誤差很小，起升動(dòng)載的表達(dá)式能夠很好地反映其起升動(dòng)載特性。

4 結(jié)語(yǔ)

本文對(duì)懸浮抱桿的起升動(dòng)載系數(shù)進(jìn)行了研究。懸浮抱桿的質(zhì)量和剛度是影響懸浮抱桿起升動(dòng)載系數(shù)的決定性因素。本文建立了懸浮抱桿的模型，對(duì)懸浮抱桿的結(jié)構(gòu)進(jìn)行分析，利用結(jié)構(gòu)變形與剛度的關(guān)系求解了懸浮抱桿的等效剛度，分別求解出各個(gè)單元體的位置矩陣和位移矩陣，利用動(dòng)能等效的原理求解出懸浮抱桿的等效質(zhì)量。對(duì)起升動(dòng)力學(xué)模型進(jìn)行求解，得到起升動(dòng)載系數(shù)的表達(dá)式，并對(duì)表達(dá)式進(jìn)行優(yōu)化，得到更有利于工程應(yīng)用的形式。

隨后應(yīng)用有限元軟件ANSYS 對(duì)懸浮抱桿的起升過(guò)程進(jìn)行仿真，建立了□800型懸浮抱桿的模型，分別以0.50 m/s、1.00 m/s、1.50 m/s 和2.00 m/s 的速度進(jìn)行起升，求解其最大動(dòng)位移，獲得不同起升速度的起升動(dòng)載系數(shù)。將仿真值與理論值進(jìn)行比較，發(fā)現(xiàn)二者誤差很小，由此證明懸浮抱桿的起升動(dòng)載系數(shù)的表達(dá)式能夠很好地反映其起升動(dòng)態(tài)特性，為今后懸浮抱桿的設(shè)計(jì)計(jì)算提供了一定的參考。