水下圓柱殼結構流噪聲仿真及降噪技術研究

周志洪，林永水，陳 威，池晴佳

（武漢理工大學理學院，武漢 430070）

潛艇、潛水器以及拖曳聲吶等柱殼結構在海洋探測開發方面應用廣泛。由于在航行過程中，海流會使得柱形結構表面產生周期性壓力波動，激發出流噪聲，對內部人員的舒適度和設備的靈敏性會產生影響[1]。當來流與殼體垂直時，阻力系數和升力系數幅值均較大，同時噪聲顯著增大[2]。為降低流噪聲對水下柱殼結構內部設備和人員的影響，國內外學者對其流噪聲機理以及降噪技術等方面展開了相關研究。

時勝國[3]等從理論上推導出平面聲波對彈性柱殼聲的矢量聲場數學表達式，計算了不同殼體參數下水聽器的聲波接收響應幅值和相位；湯渭霖等[4]通過波數-頻率譜傳遞函數，對黏彈性圓柱殼和流體負荷整個系統進行理論推導，導出了湍流邊界層壓力起伏激勵下管內噪聲場互譜函數的一般表示式，并且用數值積分方法計算了柱殼半徑、殼厚、材料吸收及流速等因素對噪聲降低值的影響；劉國慶[5]基于大渦模擬和Lighthill聲類比理論對圓柱繞流場和聲場進行了數值仿真，得到其聲壓級隨速度和雷諾數的變化規律；呂世金等[6]對雙層加肋圓柱殼模型采用模態分析法進行研究，建立此模型水動力噪聲計算方法，并驗證了該方法的可靠性，能更好反映航行體結構聲輻射特征；王曦暉等[7]結合SST-SBES湍流模型和FW-H 聲類比方法，對水下航行器不同形狀圍殼結構的水動力噪聲進行參數化分析，得到圍殼前緣加裝填角可以有效抑制噪聲的結論。

在材料隔聲性能方面，也展開了相應的研究。張嵩陽等[8]對鍍鋅鋼板與阻尼橡膠的不同層合結構進行了實驗和數值仿真，比較了約束與自由阻尼結構的降噪性能差異，得到了降噪性能與結構層數及阻尼層厚度的關系；張道禮等[9]探討了拖曳線列陣聲納護套內流噪聲的產生機理以及護套材料聚氨酯的透聲降噪機理，分析了聚氨酯彈性體的聲學性能與材料屬性之間的關系；趙俊雅[10]對復合材料圓柱殼進行了仿真分析和實驗測試，探討了中低頻下復合材料圓柱殼鋪層角度、厚度、材料參數等對傳聲損失的影響，研究了腔內敷設聲學材料厚度、種類以及多層敷設對圓柱殼傳聲損失的影響規律。

目前研究的主要關注點圍繞圓柱殼外輻射噪聲及控制，而對降低殼內流噪聲的研究較少，且聲源信息多基于直接給定，未從聲源產生開始分析。本文以水下圓柱殼結構為研究對象，采用基于SSTk-ω湍流模型方程和Lighthill聲類比理論的混合數值模擬方法進行研究，如圖1 所示，構建流場與聲場的聯系，開展流噪聲仿真分析，并探討降噪技術。

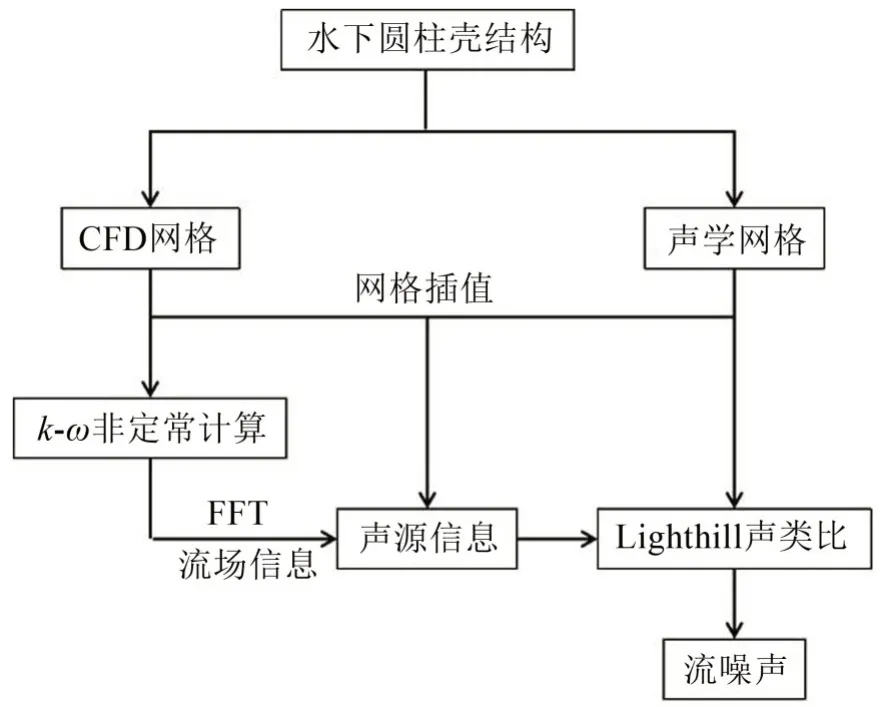
圖1 流噪聲混合數值模擬方法流程圖

1 流噪聲原理及研究方法

1.1 流場理論

本文采用的湍流計算模型為雷諾平均模擬中的SSTk-ω兩方程模型[11]。該模型較經濟且能精確捕捉壁面的分離流動，主要是通過求解兩個附加方程，即表示湍流脈動動能方程的k方程和表示湍流耗散方程的ω方程來求解湍流應力。其k、ω方程和渦黏系數如下：

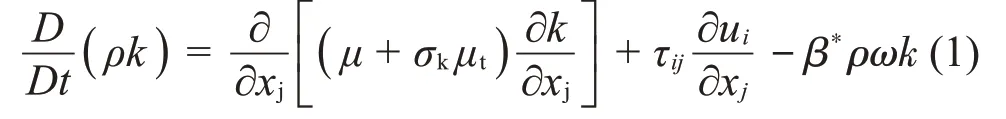
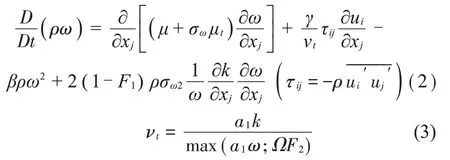
其中：Ω為渦量，F1和F2為混合函數，與點到壁面的距離有關，模型中的參數為ψ=F1ψ1+（1-F1）ψ2，第一組參數ψ1設定為a1=0.31，σk1=0.85，σω1=0.5，β1=0.075，β*=0.09，k=0.41，，對應于Wilcox 的k-ω模型，第二組參數ψ2設定為a1=0.31，σk2=1.0，σω2=0.856，β2=0.082 8，β*=0.09，k=0.41，，對應標準k-ω模型。模型中混合函數F1的作用就是完成模型由近壁面的k-ω模型到遠離壁面的k-ε模型的過渡。

1.2 聲場理論

采用Lighthill 聲類比理論，通過對納維-斯托克斯方程進行重新排列導出，從而得到了聲壓的對流標量波動方程，式子如下[12]：

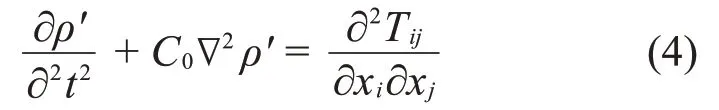
式中：ρ′表示密度脈動，即ρ′=ρ-ρ0，C0為流體中的聲速，Tij為Lighthill應力張量。

由于聲壓線性變化很大，需引出一個對數量聲壓級（Sound Pressure Level，SPL）來表示聲音的大小，并且當計算不同頻率的疊加作用時，通常采用總聲壓級（Overall Sound Pressure Level，OSPL）來表示，其定義式分別如下：

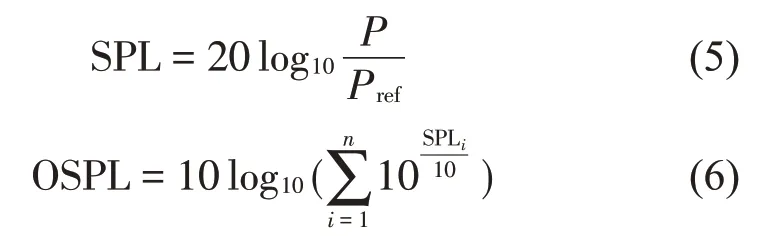
式中：P為測點聲壓，Pref為參考聲壓，在水中一般取10-6Pa，在空氣中取2×10-5Pa。

2 模型介紹及參數設置

2.1 流場模型及參數

某水下圓柱殼結構如圖2所示。當該圓柱結構遭遇橫向來流時，渦的脫落會加劇流噪聲產生。其長度較長且差異不大，而采用三維計算資源要求高，為提高計算效率，可簡化為二維流體域計算模型如圖3所示。圓心位于坐標原點處，直徑D為2.1 m，流場長35D，寬為20D，原點距左端的來流邊界10D，距上下對稱邊界各10D，即此時可忽略邊界對流場的影響[13]。將左側來流邊界設為速度入口，U=1.675 m/s，右側設置為自由出口邊界，上下側為對稱邊界，圓形外壁設為靜止壁面。流體介質為水，其密度為998.2 kg/m3，運動黏度為1.004×10-6m2/s2，參考壓力為105Pa。由公式（4）可知該流域雷諾數Re=3.5×106，屬湍流態，所以選用SSTk-ω模型。根據網格尺寸、來流速度以及庫朗數（Courant Number）要求，取計算時間步長為0.01 s。

圖2 某水下潛器結構示意圖

流場計算域采用全四邊形的結構化網格，如圖3所示。圓形壁面附近的流動情況比較復雜，因此在其壁面設置邊界層網格，最小尺寸為10-6m，滿足庫朗數小于1的要求[14]，使流場能充分穩定地發展。網格密度由圓形附近向計算域四周邊界逐漸減小，既保證能捕捉到流場信息，又降低了計算量。

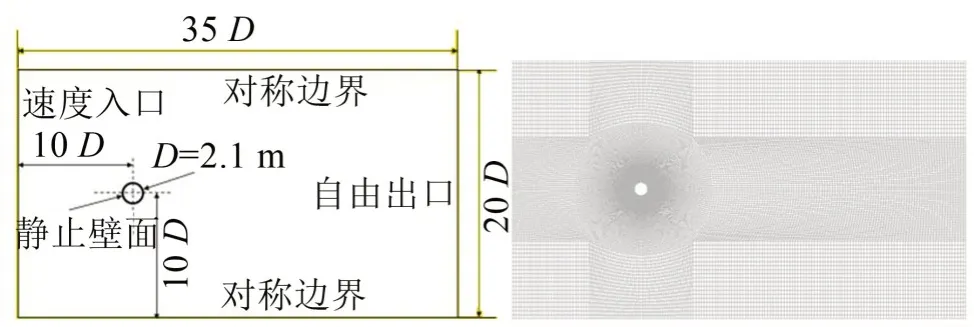
圖3 外流場域計算模型及網格

2.2 聲場模型及參數

圖4為聲場計算域示意圖。聲源域（深色區域）為流場結果的插值計算區域，即Lighthill 聲類比計算域；傳播域（淺色區域）是將流場四個邊界外推長度D的區域和潛水器內部區域；無限域為最外層邊界，用于模擬無限遠處無反射邊界，即圖中虛線部分。圓柱殼結構為圖4 中陰影部分，外徑為2.1 m，取壁厚為23 mm。聲學覆蓋層布置在圓柱殼外側，其厚度為20 mm。

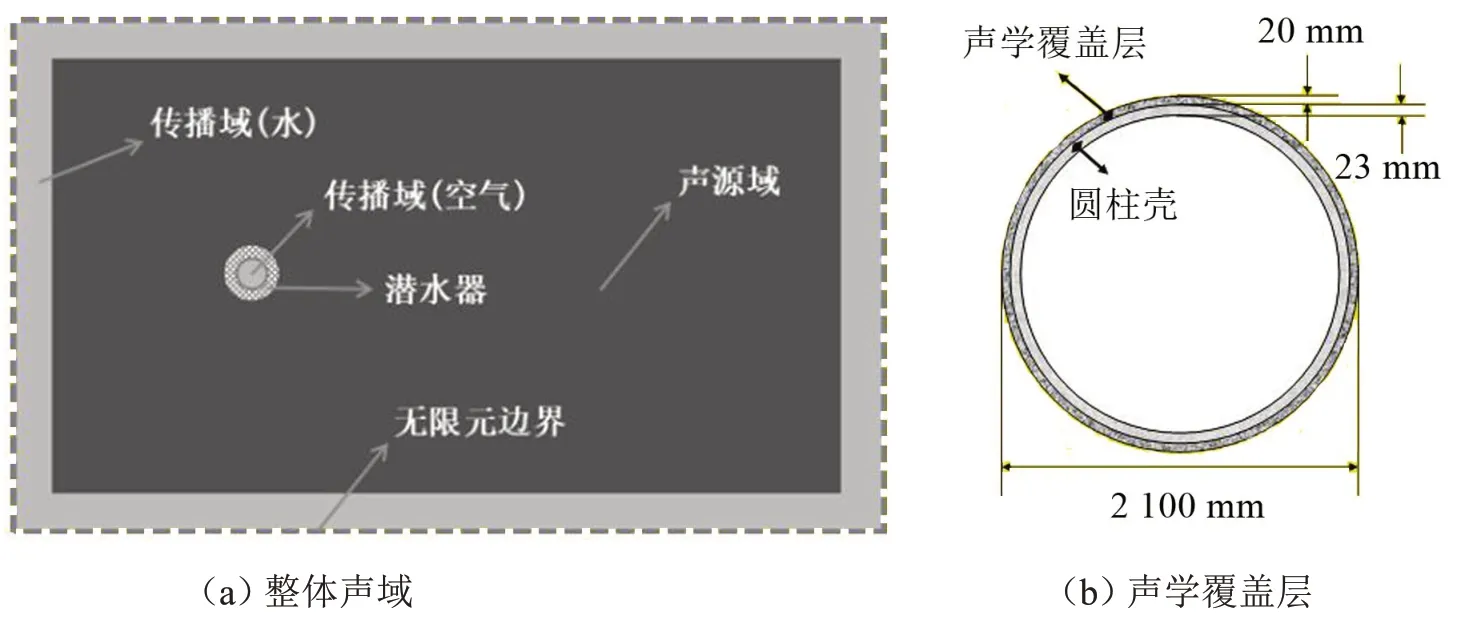
圖4 聲場計算模型

采用有限元法進行聲學計算，其網格尺寸應小于波長的六分之一。潛水器材料選用鈦合金（Ti-6Al-4V），密度為4 430 kg/m3，彈性模量為113.8 GPa，泊松比為0.342；外部流體介質為水，聲速為1 500 m/s；內部流體介質為空氣，密度為1.225 kg/m3，聲速為340 m/s。

3 流場分析

3.1 無量綱數

雷諾數Re為流體流動時的慣性力和黏性力之比，定義式如下：

式中：ρ表示流體密度，U表示來流速度，d表示特征長度，μ表示流體運動黏度。

升力系數CL、阻力系數CD分別是物體所受到的升力或阻力與氣流動壓和參考面積的乘積之比，壓力系數CP是用來表征流場中某點的相對壓力，定義式如下：

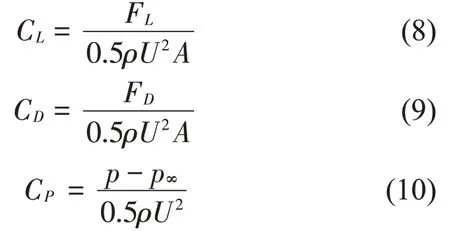
式中：FL，FD分別為物體所受升力和阻力，ρ為流體密度，U為來流速度，A為物體的特征面積，p為所求點靜壓，p∞為遠離擾動的靜壓。

斯特勞哈爾數St為當地慣性力與遷移慣性力之比，定義式如下：

式中：fv表示渦脫落頻率，d表示特征長度，U表示來流速度。

3.2 結果比對

升力系數CL和阻力系數CD的時程曲線和頻譜曲線如圖5 所示。升力系數的頻率為0.25 Hz，阻力系數的頻率為0.5 Hz，存在兩倍關系。

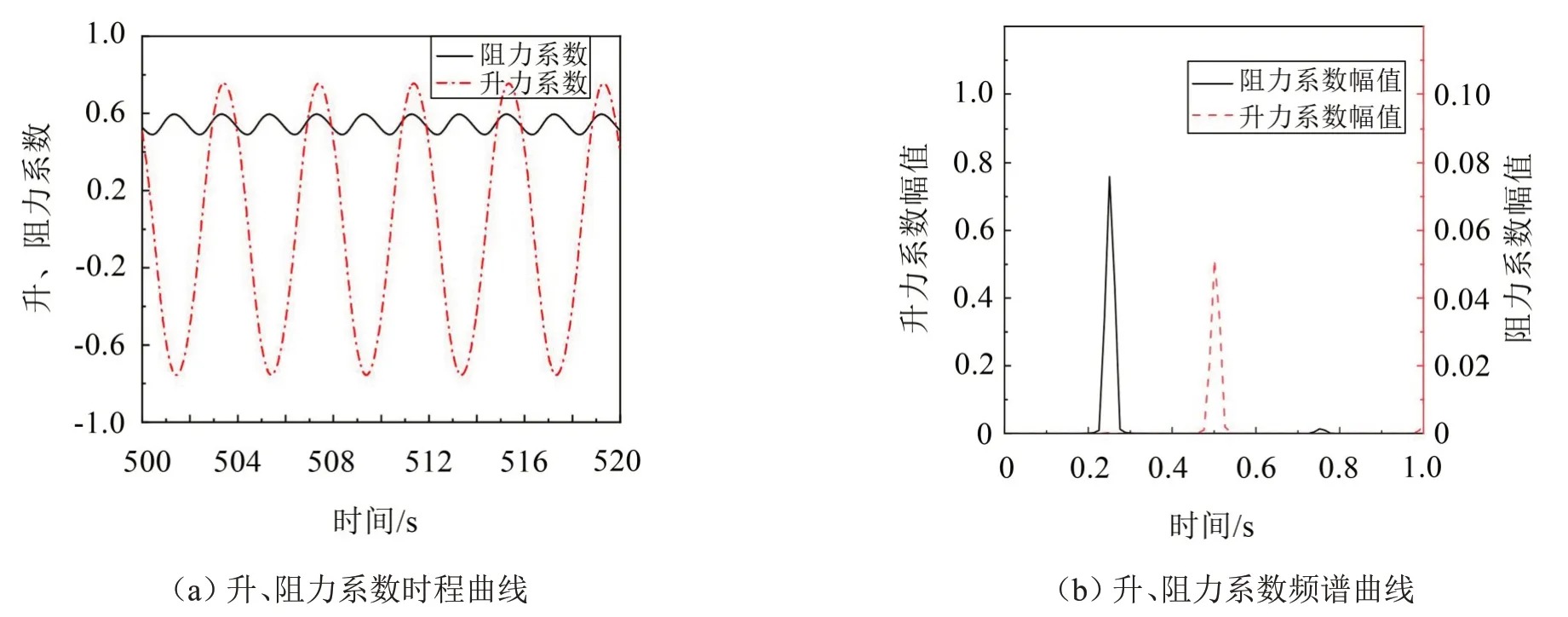
圖5 圓柱殼表面升、阻力系數曲線

阻力系數均值和斯特勞哈爾數如表1所示。與前人研究結果對比吻合較好，表明本文建立的計算模型是可靠的。

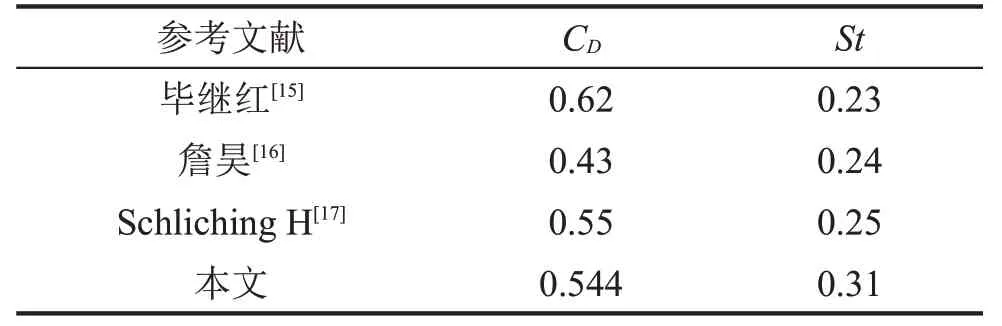
表1 Re=3.5×106的圓柱繞流計算結果

殼體表面的脈動壓力分布如圖6 所示，壓力系數CP取圓柱殼不同角度表面壓力的平均值。由于對稱性只取圓柱殼上半部分，從圖中可以看出圓柱殼在來流方向的正表面壓力最大，垂直方向會產生負壓，這也是升力產生的原因。

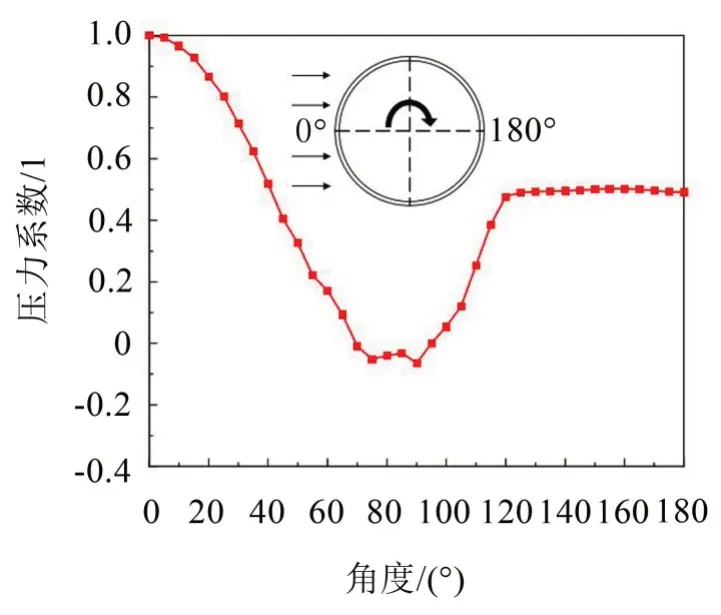
圖6 圓柱殼表面平均壓力系數圖

圖7 為流場的渦量變化圖，渦交替脫落，且正、負渦對稱。由于升力和來流方向垂直，而阻力是與其平行的方向，所以無論是上表面的渦還是下表面的渦脫落，阻力方向不變，升力則方向相反。因此在一對渦脫落周期即升力變化周期內，阻力兩次達到最大峰值，與圖5 中阻力系數頻率為升力系數頻率的二倍關系符合，升力系數頻率即為渦脫落頻率。

圖7 不同時刻圓柱渦量圖（T為渦脫落周期）

4 聲場分析

4.1 場點設置

設置6個聲學監測點，位置分別為1（0，0）、2（-D，0）、3（D，0）、4（0，D）、5（0，-D）、6（10D，0），其中測點1為殼內中心，測點2、3 的位置關于測點1 左右對稱，測點4、5則關于測點1上下對稱。

4.2 聲場特性

研究分析流噪聲的特性，不考慮流體激勵殼體的振動輻射噪聲。圖8 和圖9 分別為f=0.25 Hz、f=0.5 Hz 時無聲學覆蓋層的聲場云圖和輻射特性曲線。

圖8 中其聲場分布上下對稱，聲壓最大值主要集中圓柱周圍和尾渦區域。由于接近升力系數頻率，內部聲場分布也上下對稱，指向性與四極子聲源的指向性相近，說明此頻率下圓柱繞流噪聲主要是尾渦中的湍流壓力所產生的四極子聲源引起。

圖9 與圖8 的聲場云圖不同，對應阻力系數頻率，而阻力系數的幅值比升力系數小，從而導致其聲源域聲壓較低，并且內部聲場分布左右近似對稱，與阻力方向對應，指向性與偶極子聲源的指向性相近，說明此頻率繞流噪聲主要是壁面的壓力脈動所引起的。

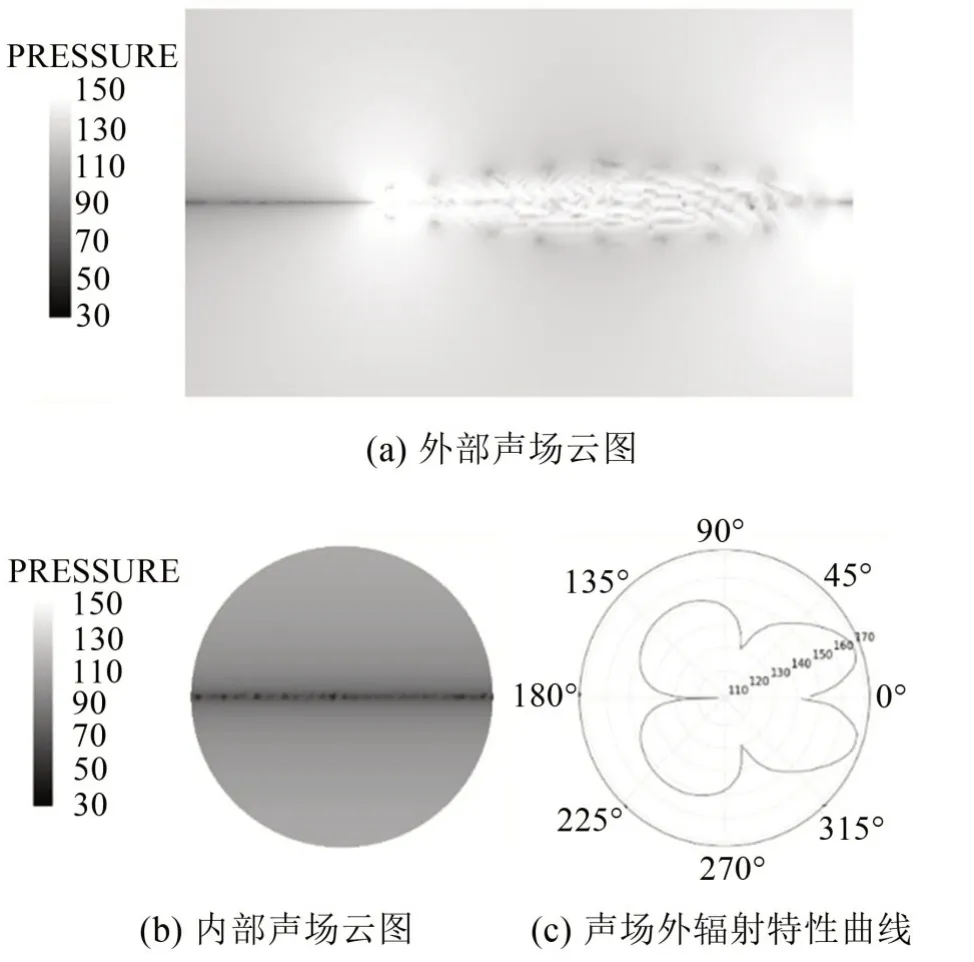
圖8 f=0.25 Hz時聲場特性

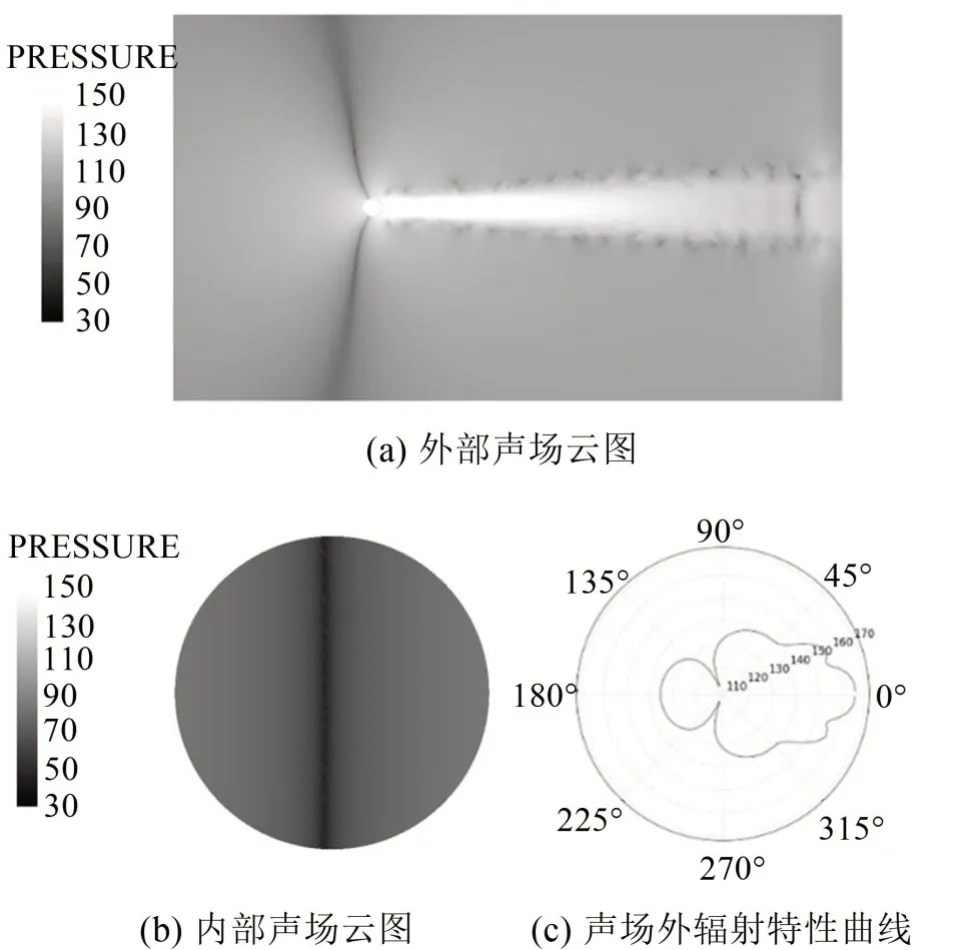
圖9 f=0.5 Hz時聲場特性

表2為無聲學覆蓋層各測點的總聲壓級。測點4和測點5的位置關于來流方向對稱，因此其總聲壓級結果相近。圓柱后側的測點3 比前側的測點2 的總聲壓級大，主要是由于尾渦脫落產生湍流應力噪聲作用的結果。而對比同位于圓柱后側的測點3和測點6，發現越靠近圓柱后壁聲壓越大，遠場聲壓逐漸衰減，圓柱壁面的脈動壓力噪聲是主要聲源。

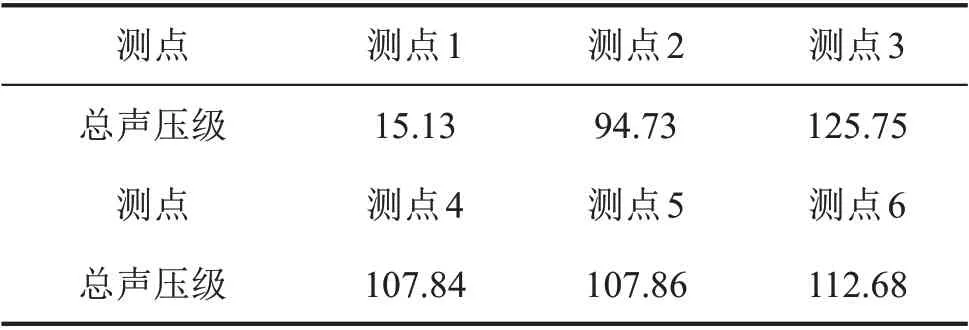
表2 各測點總聲壓級/dB

4.3 不同材料的降噪性能

圓柱殼結構聲學覆蓋層分別是鉛板（Pb）、聚氨酯彈性體（Polyurethane Elastomer，PUE）、聚氨酯泡沫（Polyurethane Foam，PUF），厚度取20 mm，其材料參數見表3、表4。

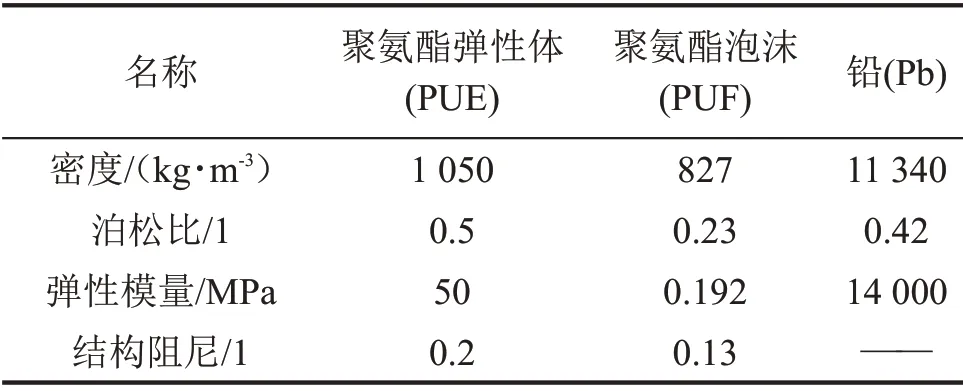
表3 覆蓋層材料參數

表4 聚氨酯泡沫材料聲學參數

取內部噪聲較大點（0，1）為監測點，聲壓級頻譜曲線如圖10所示，圓柱繞流的流噪聲主要發生在低頻段，并且在0.25 Hz和0.5 Hz左右聲壓級出現了尖峰，因為該頻率為渦脫落頻率，當渦從圓柱表面脫落時，壓力起伏會產生較大的流噪聲。

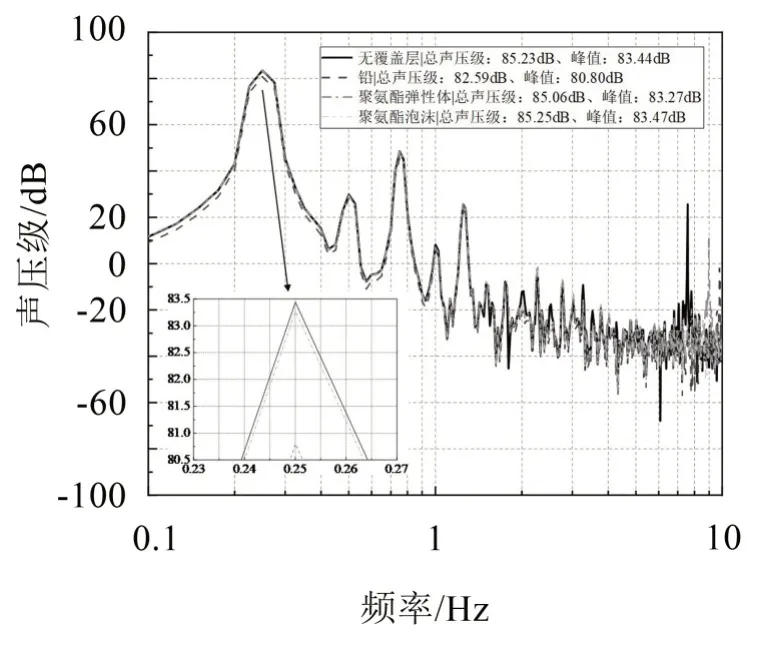
圖10 不同材料覆蓋層聲壓級頻譜曲線

PUE、PUF 和鉛的總聲壓級分別為85.06 dB、85.25 dB 及82.59 dB，鉛的降噪性能最佳，且在峰值處降低2.64 dB。由于鉛相對于其他兩種材料密度很大，根據質量密度定律和阻抗失配理論，聲更不容易透過，而PUE 和PUF 的聲壓級都較大，說明其在低頻段降噪效果不佳，但采用鉛會大幅增加重量。

4.4 不同厚度比覆蓋層的降噪性能

取6 種不同組合方式（從外到里）：Pb-PUE（1:1、4:1、9:1）、Pb-PUF（1:1、4:1、9:1），覆蓋層總厚度與監測點不變，探究不同厚度比覆蓋層的降噪性能。由于鉛降噪性能優良，與水的阻抗相差較大，因此將它作為最外層的覆蓋層。

在這6 種不同層合結構的聲學覆蓋層中，如圖11 至圖12 所示，Pb-PUE 與Pb-PUF 都是在9:1 的比值下聲壓級最低，并且比值越大降噪性能越好，其主要原因是鉛主要依靠其自身密度減弱聲能，受厚度變化影響較大。PUE 是通過自身阻尼減振吸聲，PUF是靠內部孔隙吸聲，兩者受厚度影響均較小，所以在低頻噪聲下，鉛占比越大的組合更能發揮出它的降噪性能。綜合考慮經濟性和輕量化，選擇合適的厚度比，既能有效降噪又不會顯著增加重量。

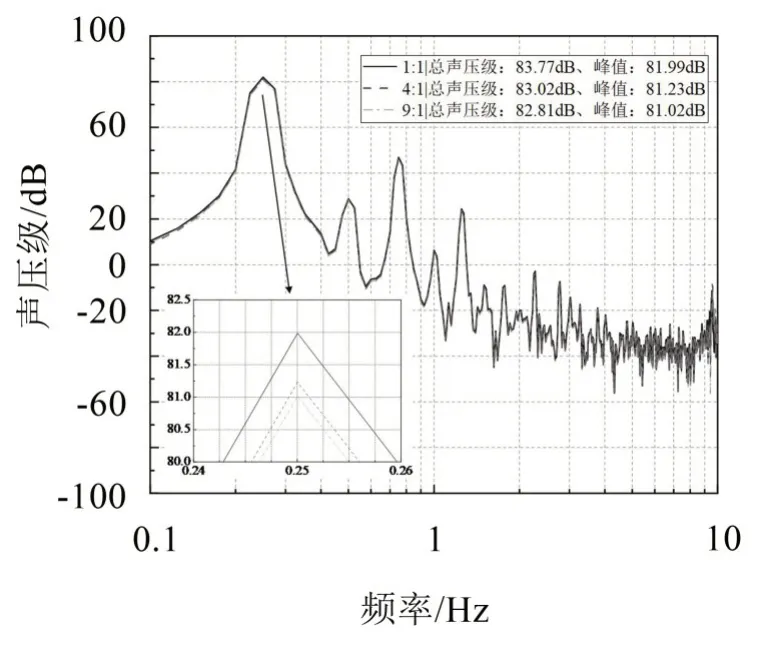
圖11 Pb-PUE覆蓋層聲壓級頻譜曲線

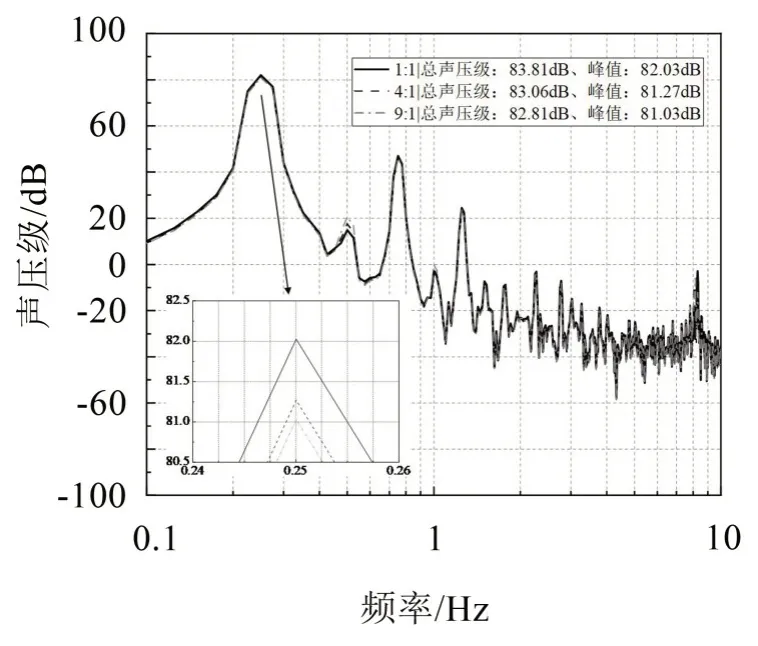
圖12 Pb-PUF覆蓋層聲壓級頻譜曲線

4.5 不同厚度空氣層的降噪性能

由4.3節知鉛覆蓋層的降噪性能最佳，而空氣又經常用來作為隔聲夾層。保持總體厚度20 mm 不變，在鉛和圓柱殼之間增加空氣層，由36 個弧長為10 mm 的同種材料等角度支承，改變空氣層的厚度以探究不同結構對流噪聲傳播的影響。

如圖13 所示，在空氣層厚度為2 mm、4 mm、10 mm的結構中，2 mm空氣層降噪性能最好，其聲壓級峰值為79.50 dB，比鉛層的峰值聲壓級80.80 dB 還要小，說明在覆蓋層內加空氣隔層能有效減弱聲壓級峰值，提高降噪性能，還可以減輕重量。

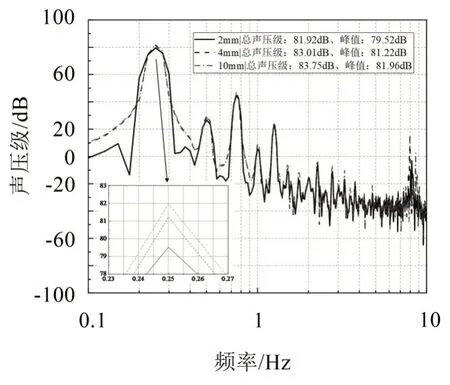
圖13 不同厚度空氣層聲壓級頻譜曲線

5 結語

研究結論如下：

（1）流噪聲的峰值頻率與渦脫落頻率一致，主要是由于渦脫落導致流體壓力脈動激發噪聲占主體，集中在低頻段，聲場輻射特性與理論情況相符。

（2）采用PUE、PUF 和鉛三種聲學覆蓋層吸隔流噪聲，鉛性能最佳，PUE、PUF次之，并且該三種材料組合的合理厚度比，既可以有效降低噪聲又能顯著減輕重量。

（3）空氣層對低頻噪聲的阻抑效果顯著，且鉛內空氣層厚度適當時，能有效削弱流噪聲峰值，抑制流噪聲向結構內部傳播。