GASA-PSO優化算法共振稀疏分解齒輪故障診斷研究
高永新,戴忠林,秦 燦
(遼寧工程技術大學機械工程學院,遼寧阜新 123000)
齒輪箱作為重要的動力傳動部件廣泛應用于旋轉機械,在復雜工況條件下,測得齒輪箱的振動信號往往呈現出高噪聲與非平穩性[1-2]。因此,從齒輪箱的非平穩振動信號中分理處出瞬態沖擊信號,通過對分離出的瞬態沖擊信號進行分析提取出準確的故障信號具有重要的研究意義。
現有齒輪箱故障信號分解方法主要有集合經驗模態分解[3]、固有時間尺度分解[4]等。Selesnick[5]提出信號的共振稀疏分解方法(Resonance-based Sparse Signal Decomposition,RSSD),該方法可根據信號成分的振蕩次數對信號進行分解與重構,實現信號的共振稀疏分解。夏俊[6]等利用松鼠優化算法計算效率與全局尋優能力的優越性,實現對共振稀疏分解的多參數優化,從而獲得故障信號的特征頻率。李星,張文義,陳向民等[7-9]提出了基于信號共振稀疏分解與包絡譜的齒輪故障診斷方法,實現了將沖擊脈沖從齒輪振動信號中分離,進而對齒輪狀態和故障進行識別;朱靜等[10]提出一種基于共振稀疏快速獨立分量的分析方法來診斷行星齒輪箱故障,得出的高共振分量作為虛擬通道信號,兩通道信號輸入固定點算法處理,選擇峭度值最大的分量Z做包絡譜分析,提取故障特征頻率。
為解決復雜工況下齒輪箱的振動信號由周期性故障引發的振動響應與隨機噪聲疊加組成而引起早期微弱故障信息不明顯、故障特征值難以提取的問題,本文將品質因子可調小波變換(Tunable-QWavelet Transform,TQWT)的低品質因子分量與原始信號的互關度作為遺傳模擬退火算法(Genetic Algorithm Simulated Annealing,GASA)與粒子群算法(Particle Swarm Optimization,PSO)的融合算法的優化對象,提出基于GASA-PSO 優化算法的共振稀疏分解齒輪故障診斷方法。
1 振動信號的共振稀疏分解
共振稀疏分解是將振動信號的振蕩次數作為分解的依據將信號分離開來。當TQWT 得到高、低品質因子為Q1,Q2的小波基函數集合SH、SL后,振動信號y經共振稀疏分解后表示為:
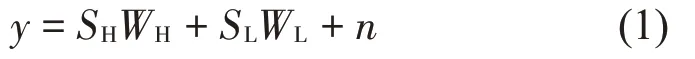
式中:WH、WL為高低共振分量系數矩陣,n表示殘差分量。
共振稀疏分解通過人為經驗直接給定品質因子Q與冗余因子r設計小波,由Q和r可得到尺度因子β和α如下式(2)所示:
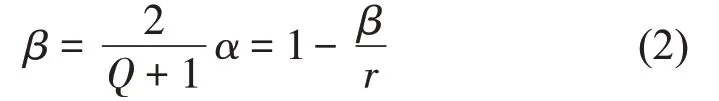
輸入振動信號中第j個子帶的中心頻率fc和帶寬BW由下式計算:
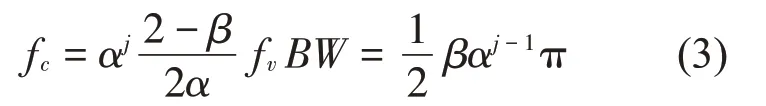
對于長度為L的輸入信號,其最大分解層數由下式確定:
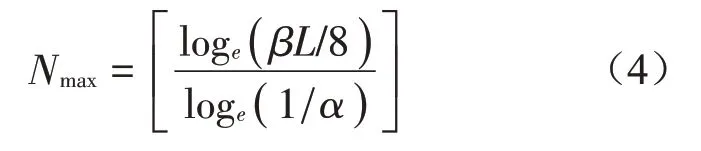
利用形態變量分析建立了耗散函數J如下式所示:
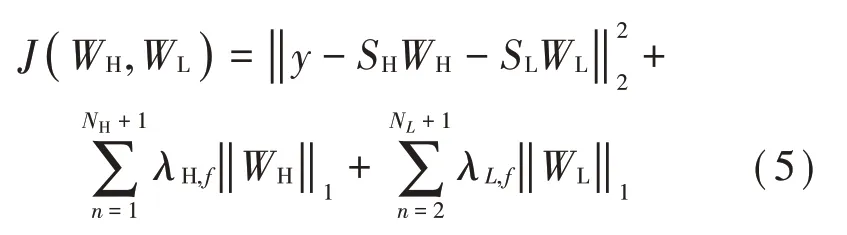
式中:λH,f、λL,f為權值系數;NH、NL為分解級數。
由于系數矩陣W的范數不可微,應用分裂增廣拉格朗日算法更新迭代系數矩陣W使耗散函數J最小,從而得到最優的系數矩陣WH*和WL*[11]。
應用RSSD 方法對輸入信號進行分解時,由品質因子Q決定的小波基函數庫是共振系數分解能否取得理想分解效果的基礎[12-13]。傳統的RSSD 通過先驗知識給定品質因子Q的值,主觀性強,無法保證給定最優匹配因子,建立最優小波基函數庫,從而影響分解效果。
2 GASA-PSO優化的共振稀疏分解
由上述分析可知Q品質因子的選取對RSSD 的分解效果起著重要作用。針對上述不足,本文提出GASA-PSO 融合算法選取TQWT 分解重構后的低共振信號與初始信號的互相關度即低共振分量峭度為融合算法的目標函數,對品質因子Q的選擇過程進行優化。
齒輪早期微弱故障特征存在于低共振分量中,低共振分量相關峭度計算公式如式(7)所示:
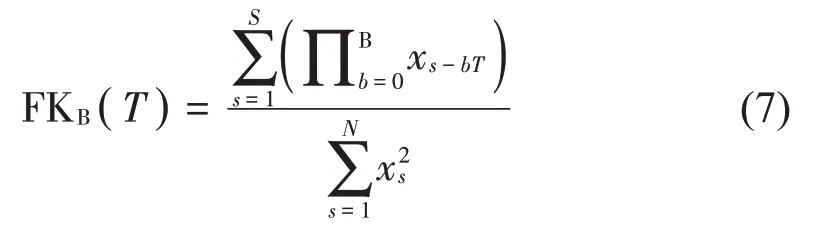
式中:x為信號源;S采樣長度;T為故障脈沖信號周期;B為采樣周期偏移數。
為避免因故障脈沖信號與采樣長度S差距不大而造成的高低共振分量信號混淆,導致分離效果差的問題,引入兩個信號的相關系數F做如下約束:
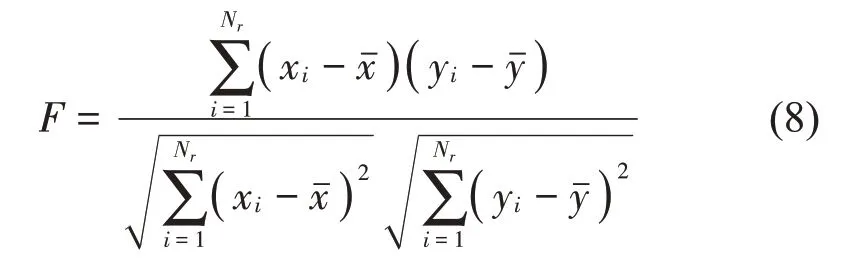
因此,本文選取經低共振分量與相關系數F做比值后的K作為適應度函數,式(7)、式(8)可得到共振稀疏分解的優化目標適應度函數:

GASA 算法在設置好退火平衡條件等操作后,GASA算法需經較多迭代次數后得到最優個體需要較長的計算時間且分離效果較差。為精確分離齒輪箱早期微弱故障信號,將GASA 算法與尋優速度較快的PSO算法融合,并作出如下改善:
(1)融合算法的底層利用GASA 的全局搜索能力來計算初代種群粒子的適應度,對較大的適應度粒子進行退火操作。上層利用PSO算法的局部搜索能力,將底層精英群體作為PSO 初代種群。設定在第q次迭代過程中,粒子i的適應度之差如下式所示:
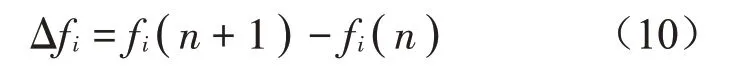
(2)上層PSO算法更新迭代計算下一代粒子的適應度,利用GASA 引入時變溫度T(t),使粒子群算法具有接受次最優解得可能,迭代更新后的適應度被接受的概率P計算方法如下:
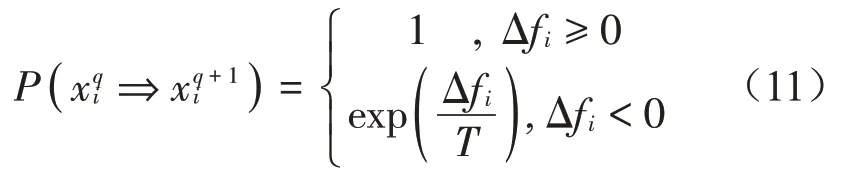
(3)慣性權重因子ω影響PSO 算法的尋優性能,當PSO 迭代次數增加、ω值線性減小時,PSO 尋優效果最好。設K為最大迭代次數,則ω的取值為:
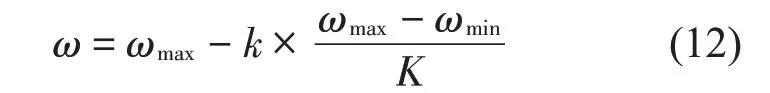
融合后的GASA-PSO 算法既具備了快速收斂的能力,又具有了全局尋優能力。在GASA 得到精英群體的基礎上,經PSO算法搜尋最優解,提高齒輪早期微弱故障信號的分離效果。融合算法的步驟如下所示:
融合算法步驟如下:
(1)設置QH在0~30之間取值,QL在0~10之間取值。保持QL區間不變,截取QH從而建立C個種群。
(2)設置初始溫度,初始解的狀態,種群數量為50;交叉概率0.25;變異概率0.008;達到最大遺傳代數300 后,以Tn+1=αTn的形式進行退火操作,選取精英個體。
(3)初始化精英群體粒子速度,最大迭代次數300,設置粒子群個體選擇條件,同樣以可調品質因子小波變換的低品質因子分量與原始信號的互關度作為個體適應度,
(4)判斷是否可以終止,若終止,輸出結果,若不可終止,替換個體,重復上述步驟。
采用融合GASA-PSO 對RSSD 的品質因子Q的選擇過程進行優化,能夠消除傳統RSSD 方法的不足,提高齒輪早期微弱故障信號的共振分量的分離效果。
3 仿真分析
為驗證本文所提方法的可行性,以齒根裂紋故障為例,分析GASA-PSO 融合優化算法的共振系數分解故障診斷方法的有效性。
3.1 齒輪裂紋故障信號振動特性分析
齒輪傳動過程中正常和異常狀態下振動信號有較大的差異。為驗證基于GASA-PSO 算法的共振稀疏分解提取故障沖擊響應的有效性,將齒輪振動信號嚙合頻率的分量作為齒輪故障信號[14]。
當齒根發生裂紋故障,固有頻率與嚙合頻率作為振動信號的載波,振動信號的幅值調制和頻率調制皆為轉頻調制[15],故障齒輪振動信號響應表達式為:
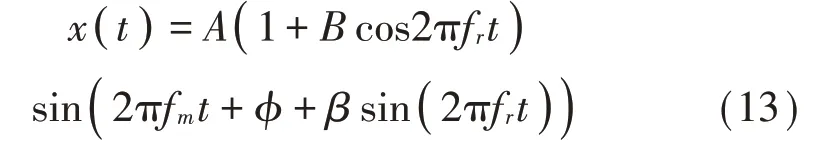
式中:B為幅值系數;β為頻率系數;fr為故障軸轉頻。
設置齒輪箱中為一對相互嚙合的齒輪,輸入軸齒輪的齒數為19,輸出軸齒輪的齒數為48。電機轉速為1 800 r/min,輸入軸的頻率為30 Hz,嚙合頻率為570 Hz,采樣頻率為10 000 Hz。采用MATLAB軟件中的ode15 s 法求解齒輪箱動力學方程可得到齒輪箱系統的動力學響應[16]。
對比觀察圖1中2幅頻譜圖可以發現:頻率主要成分是齒輪副的嚙合頻率fm及其倍頻2fm、3fm等,各倍頻之間存在邊頻帶,隨著裂紋深度的增加,其倍頻幅值增大,邊頻帶在各個倍頻間的振蕩明顯,幅值增大。
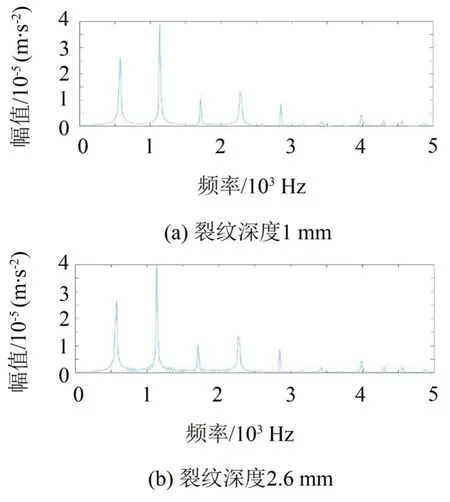
圖1 不同裂紋深度主動輪的頻域圖
由上述分析可知,可根據邊頻帶的分布區間和幅值判別齒根裂紋故障程度,為齒輪副的早期微弱故障診斷提供理論支持。
3.2 信號仿真分析
在進行齒輪箱故障診斷時,采集的齒輪裂紋故障特征信號中裂紋等故障信息會以周期性沖擊脈沖的響應的形式表現,根據分析發現此脈沖的頻率一般為齒輪轉頻或其倍頻,因此,以此作為故障特征的基準進行提取。根據上文分析的齒輪箱齒根裂紋故障,利用MATLAB以上文故障齒輪振動信號模型來驗證GASA-PSO 融合算法優化后共振稀疏算法對齒輪故障振動信號分離的有效性。設置一組衰減系數為-420,載波頻率為520 Hz,調制頻率為100 Hz的周期性衰減脈沖信號,對該信號設置兩組幅值為3 mm/s2和2 mm/s2,頻率為1 560 Hz與1 380 Hz的正弦信號進行調制,調制后信號如圖2所示:
圖2為進行調制處理的正弦信號和隨機噪聲疊加信號,無法分析脈沖信號的特點。如圖3 所示為采取融合算法優化的共振稀疏分解處理后的高、低共振分量信號及殘差分量信號。齒輪箱早期微弱故障信號特征主要存在于低共振分量信號中,故對此分量信號做希爾伯特變換后,利用findpeaks 函數提取調制后信號中故障特征,繪制包絡譜圖如圖4、圖5所示。
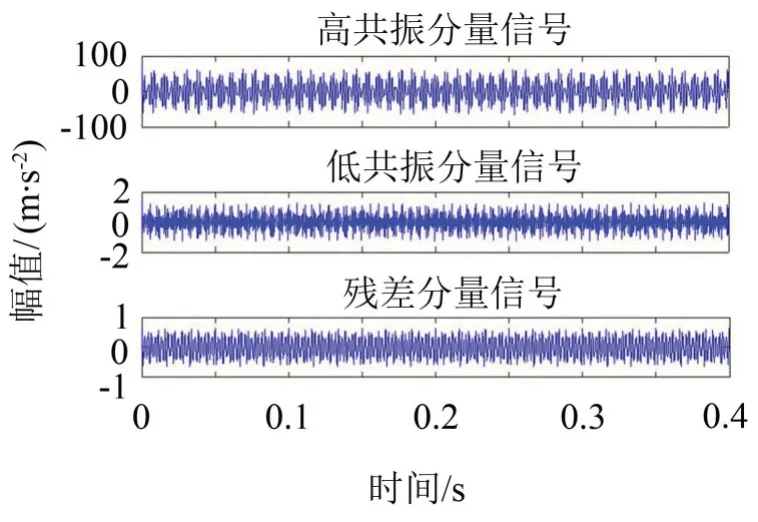
圖3 模擬仿真信號分解后各分量時域波形圖
如圖4所示,高共振分量主要由頻率為1 380 Hz和1 560 Hz的兩組正弦信號疊加而成。
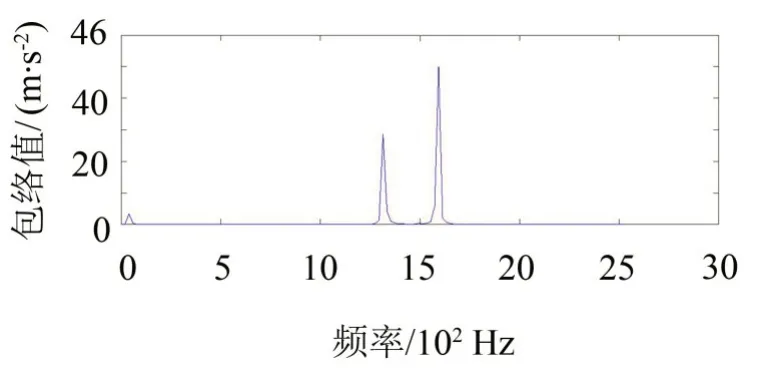
圖4 GASA-PSO高共振分量的頻譜分析
如圖5至圖6所示,振動信號的低共振分量經過頻譜分析后可直觀地發現,GASA-PSO 優化算法低共振分量包絡譜中含有調制頻率為100 Hz 的脈沖信號及其倍頻,與GASA 算法優化后的低共振分量包絡譜相比,周期性沖擊清晰可見,分離效果較好,整體的規律性較強,與理論貼合度較高。該方法能夠依據高、低共振分量故障特征頻率準確地分離出故障特征,從而對早期齒根裂紋故障進行診斷。
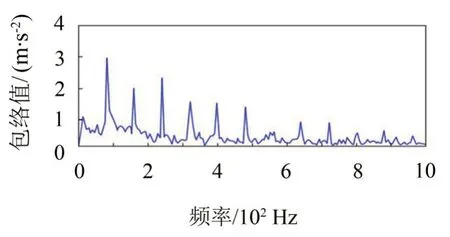
圖5 GASA-PSO 優化算法低共振分量包絡變換譜
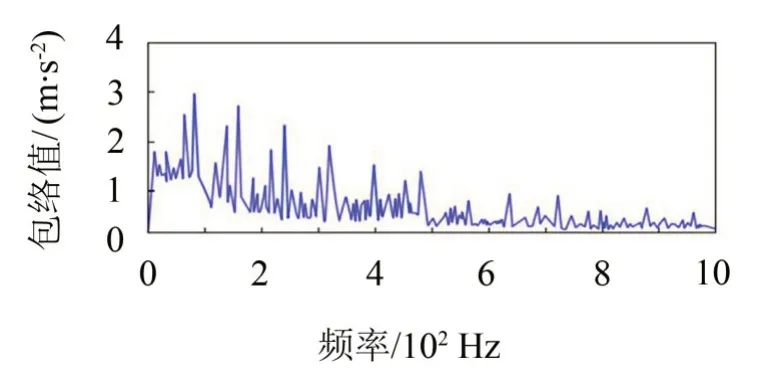
圖6 GASA優化算法低共振分量包絡變換譜
4 實驗分析
4.1 實驗設計
為驗證基于GASA-PSO 融合算法的共振稀疏分解的風機齒輪箱故障特征提取方法的有效性,設計如下實驗方案:
平行軸齒輪箱故障數據實驗測試平臺如圖7所示,將存在裂紋故障的齒輪安裝在齒輪箱內,平行軸齒輪箱通過聯軸器與變速驅動電機和磁力制動器連接,電機反裝齒輪箱和聯軸器驅動齒輪箱完成實驗,振動加速度/速度一體化傳感器測量驅動軸輸入端、輸出端的軸向和徑向振動信號。表1給出平行軸齒輪箱齒輪傳動部分齒數。

圖7 平行軸齒輪箱故障數據實驗測試平臺

表1 平行軸齒輪箱傳動參數
4.2 實驗數據分析
選取驅動軸輸出端測點作為振動原始信號,通過振動傳感器采集到振動原始信號如圖8 所示,雖可隱約看出信號中存在脈沖成分,但受其復雜工況影響,規律性較弱;對振動傳感器采集到振動信號進行GASA-PSO 融合算法的共振稀疏分解特征提取后,如圖8得到圖9。
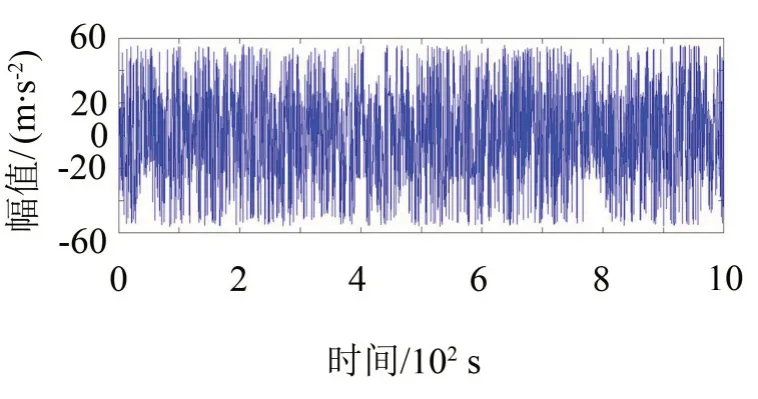
圖8 振動原始信號
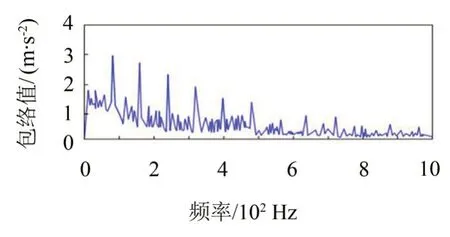
圖9 實驗信號共振稀疏分解后低共振分量包絡譜
如圖9 所示,采用融合GASA-PSO 優化的共振稀疏分解法可有效提取風機齒輪故障特征信息。圖9低共振分量中主要包含調制頻率為100 Hz的脈沖信號及其倍頻信號。低共振分量包絡圖呈現fm及其倍頻的故障頻率,故障特征明顯,分解效果理想。
本文所提出的GASA-PSO 優化算法的共振稀疏分解方法可實現品質因子Q與故障振動信號脈沖成分最佳的匹配,可有效地提取故障特征。
5 結語
(1)研究齒根裂紋對齒輪副振動特性的影響發現齒根裂紋故障對齒輪副的振動響應影響會隨著裂紋深度的增加而越來越明顯,通過觀察頻域圖中邊頻帶的分布區間和幅值可以判別齒根裂紋故障的嚴重程度。
(2)品質因子的選取在共振稀疏分解的過程中有著重要的作用,會影響分離齒輪故障信號的瞬態沖擊信號的效果。利用融合GASA-PSO 算法底層的全局尋優與上層的局部尋優從而獲得更好的尋優效果,在可取的范圍自適應選擇最匹配品質因子是行之有效的方法。通過仿真試驗與實驗的方法證明,該算法具有較好的抗噪性,能夠準確地分解信號,進而提取復雜信號中的故障信息,為故障診提供依據。

