基于SVMFE的往復壓縮機氣閥故障診斷方法

李純輝，馬永財，徐國林，趙海洋，趙海峰

（1.黑龍江八一農墾大學工程學院，黑龍江大慶 163319；2.東北石油大學機械科學與工程學院，黑龍江大慶 163318）

往復壓縮機振動信號呈現出非平穩、非線性的特性，且故障信號中包含著大量的噪聲信號，直接提取故障特征難度較大，如何有效地提取出往復壓縮機的故障特征是目前往復壓縮機故障診斷的熱點和難點。隨著非線性理論的發展，眾多學者對非線性分析方法的研究已逐漸成熟，分形維數、混沌時間指數、Lyapunov指數及信息熵等分析方法被提出[1-7］，目前已廣泛應用到往復壓縮機故障診斷中。Zhao等[8]提出基于多重分形的SVD故障特征提取的方法，實現了對往復壓縮機軸承間隙定量描述；趙海峰等[9]提出基于奇異值與近似熵劃分階段的方法來提取故障數據，得到了分段后信號的近似熵更具有相對一致性；針對近似熵在熵值計算中存在自身匹配的問題，Richman等提出了樣本熵[10]，樣本熵在避免自身匹配問題的同時，在相對一致性上更為優秀，能夠衡量序列的無規則程度。樣本熵在信號復雜程度的描述上比較單一，不能全面地反映出不同尺度下的特征信息，Costa 等[11]在樣本熵的基礎上提出多尺度熵，用以描述不同元素在多尺度因子下的序列的結構復雜程度和自身之間的相關性。陳偉婷[12]在深入研究樣本熵的理論基礎上，針對樣本熵中存在的問題，將模糊集的基本概念與樣本熵有機地結合，提出了帶有模糊集的熵，即模糊熵。模糊熵與樣本熵相比，熵值變化波動較小，不會存在突然失去熵值的問題，連續性和相對一致性方面都更優越。在模糊熵的基礎上，鄭近德等[13]借鑒多尺度熵的思想在模糊熵概念的基礎上提出了多尺度模糊熵。

MFE 集合了多尺度熵與模糊熵的所有主要優點，無論是在描述序列的完整性上還是相對一致性上均更加優越，且不受數據長度的限制，擁有所需數據短，相對一致性高等特點。但MFE在粗粒化計算過程存在以下問題：

（1）MFE 的粗粒化計算是基于均值的計算方法，這僅能反映出序列的平均幅值，缺少對信號波動性的描述；

（2）忽略相鄰點信息，數據長度變短，穩定性降低，故障信息不完整。

針對問題（1）本文將方差法代替均值法引入到粗粒化計算中；針對問題（2）本文將滑動法代替粗粒化計算。故本文提出基于滑動方差的多尺度模糊熵。最后將SVMFE 與ELM 相結合，提出一種基于SVMFE 與ELM 的往復壓縮機故障診斷方法，將其應用于氣閥故障數據的分析。實驗結果表明，本文所提方法能有效地實現氣閥故障診斷，具有較高的故障識別率。

1 SVMFE算法

1.1 MFE算法

MFE的計算步驟如下[13]：

（1）對時間序列xi={}x1,x2,…,xN，建立粗粒序列：

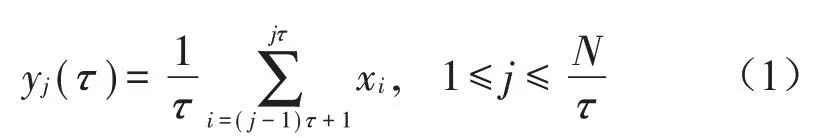
其中：τ為尺度因子，當τ=1 時，yj（1）為原序列。對于非零τ，原序列被分割成每段長為N τ的粗粒向量yj（τ）。以τ=2 為例，粗粒序列計算方式如圖1所示。

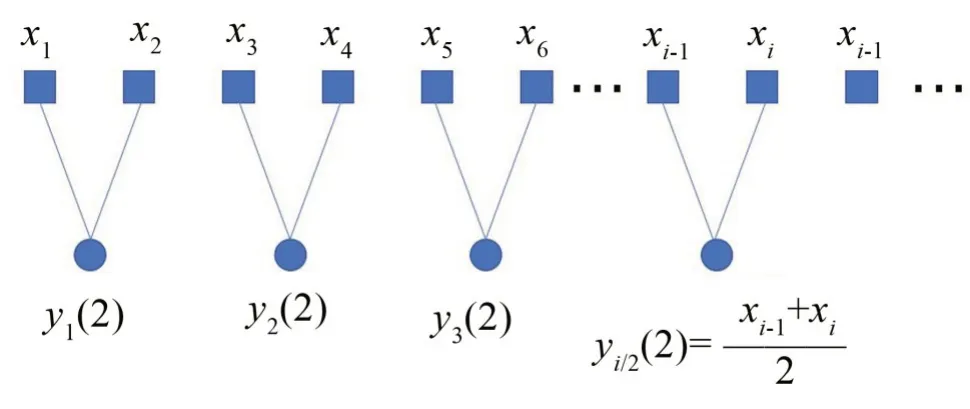
圖1 τ=2時粗粒序列計算分割圖

（2）根據文獻[13]中對模糊熵的定義，分別計算每個τ下序列的模糊熵值，稱為多尺度模糊熵。

由式（1）的粗粒化計算可以看出，粗粒序列的長度隨著尺度因子的增大而變短，穩定性會降低，熵值的偏差也會隨之變大。從圖1可以看出，當τ=2時，粗粒化序列的計算為x1和x2，x3和x4，…，xi-1和xi等之間的信息，忽略了x2和x3，x4和x5等之間的信息，導致故障信息不完整。而粗粒化計算過程實質上就是計算數據間的均值，只能反映出序列的平均幅值，忽略了信號中的波動性。針對多尺度模糊熵存在的上述缺陷，本文將滑動方差法引進到粗粒化計算中，提出基于滑動方差的多尺度模糊熵（SVMFE）方法。

1.2 SVMFE算法

SVMFE算法的具體步驟如下：

（1）對時間序列xi={}x1,x2,…,xN，建立粗粒序列：

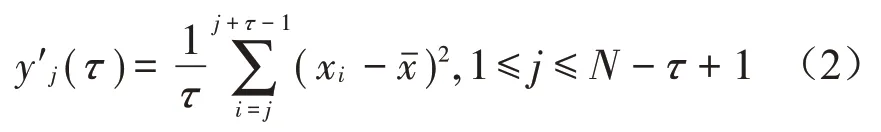
在上式中，當τ不等于1或0時，序列xi被分割成τ段長度均為N-τ+1 的粗粒向量yj′（τ）。以τ=2 為例，SVMFE中粗粒序列計算方式如圖2所示。

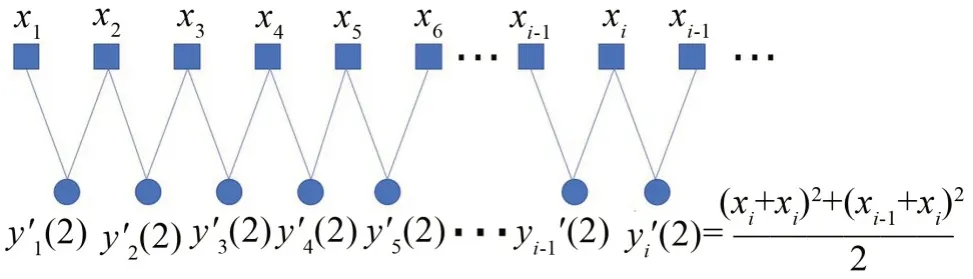
圖2 τ=2時SVMFE算法的粗粒序列計算分割圖

（2）對新序列yj′（τ）分別計算每個τ下粗粒序列的模糊熵，得到基于滑動方差的多尺度模糊熵，定義如下：

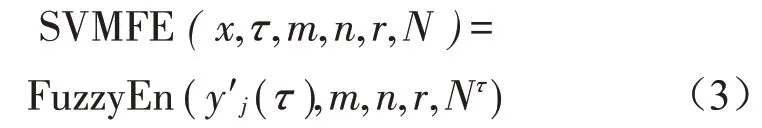
由式（2）的粗粒化計算可以看出，粗粒序列的長度與原序列相比變化小，穩定性高，熵值偏差較小，而且SVMFE算法考慮了序列中相鄰數據間的信息，避免信息泄露，同時展現出了原序列的波動性。

2 SVMFE方法仿真分析及方法對比

2.1 參數選擇

根據SVMFE的定義，其計算所需參數如下：

（1）嵌入維數m。文獻[9]表明嵌入維數越大，序列需要重構的信息越多，所需序列的長度就會越長（數據長度N的選取范圍為10 m 至30 m）。故出于綜合考慮，避免數據不足，維數m選為2。

（2）數據長度N。文獻[13]已證明在模糊熵計算中，熵值結果受數據長度N影響比較小，所取數據的長或短，都可以定義出模糊熵值，故本文便不再贅述數據長度對SVMFE 值的影響，數據長度N取2 048。

（3）相似容限r。r為函數原始時間邊界的最大寬度，r過大會使統計信息冗雜，選擇過小使統計效果不好。r的大小選取在0.1 SD 和0.25 SD 之間（其中SD為原始數據的標準差），本文中r選為0.15 SD。

（4）梯度n。梯度n決定了相似容限r的梯度，n過小會使細節信息過多，統計效果不理想，n過大會使細節信息的丟失。文獻[14]中建議在計算時n取較小的正整數，如2或3。本文梯度n選為2。

（5）尺度因子τ。為了保證粗粒序列的長度不能過短，所以τ的選擇不能過大。一般情況下取τmax≥10，本文取τmax=20。

2.2 仿真對比分析

為體現SVMFE在特征提取上的優越性，將其與MFE 對比，并采用數據長度為2 048 的高斯白噪聲為研究對象，首先以相似容限為0.1 SD、0.15 SD、0.2SD 及0.25 SD 計算兩種方法的在不同尺度下的模糊熵值，其中m=2、n=2、τmax=20，結果如圖3至圖4所示。

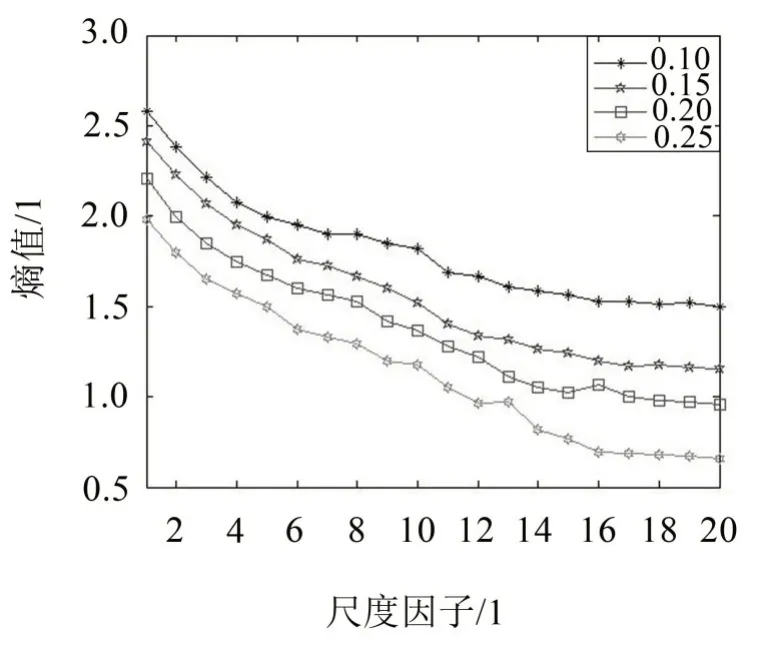
圖3 高斯白噪聲在四種相似容限下的MFE

由圖3、圖4 可以看出，兩種方法計算熵值的結果均受到相似容限的影響，都滿足r增大熵值變小的情況；但SVMFE 的熵值曲線與MFE 相比明顯更光滑，且不同相似容限下的熵值更接近，說明受相似容限的影響更小。此外可以看出，r的取值大小會直接影響序列的描述情況，通過綜合考慮，本文r取0.15 SD。

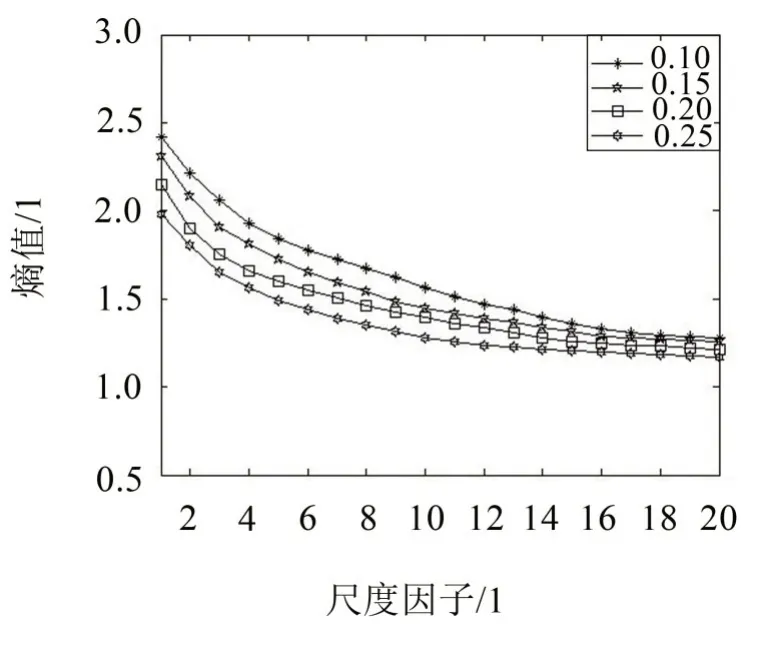
圖4 高斯白噪聲在四種相似容限下的SVMFE

為了更明顯地說明SVMFE 的優越性，選定r=0.15 SD、m=2、n=2、τmax=20 的參數條件下，計算高斯白噪聲在不同尺度下的MFE 值與SVMFE 值，兩種方法計算得到的熵值隨τ的變化如圖5所示。

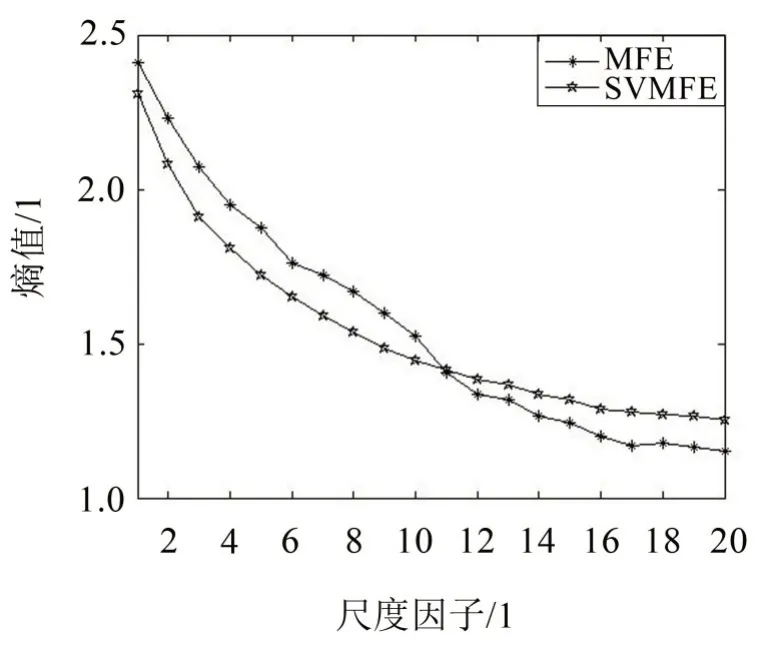
圖5 SVMFE和MFE方法下高斯白噪聲的模糊熵值

由圖5 可以看出，兩種方法的得到的熵值曲線變化趨勢相同，均是先隨著尺度因子的增大，熵值變小，然后趨近于穩定，兩個曲線的光滑性都在減弱，但SVMFE 曲線在尺度因子較大時才出現波動，而MFE 曲線出現波動的位置明顯更加靠前，說明SVMFE 的穩定性更好。綜合以上分析結果表明，SVMFE 與MFE 都能描述時間序列的復雜性，但SVMFE 受相似容限的影響較小，熵值曲線更光滑，波動更少，說明SVMFE方法在衡量序列復雜性上更準確、更穩定。

3 基于SVMFE的氣閥故障診斷

3.1 方法流程

通過以上分析，本文提出基于SVMFE與極限學習機的氣閥故障診斷方法。具體流程如下：

（1）設置k種氣閥故障狀態，將每種狀態信號隨機分為訓練集和測試集，對所有數據計算SVMFE,選取合適數量的SVMFE值作為特征向量。

（2）從每種狀態的特征向量中隨機選取i個，作為ELM分類器的訓練樣本，剩余特征向量作為測試樣本。

（3）將訓練集中各個狀態的特征向量輸入到ELM 中訓練，得到ELM 訓練模型，然后將測試集中的特征向量輸入到ELM中識別故障類型。

（4）根據ELM 分類器的輸出結果實現氣閥故障診斷。

3.2 實驗信號分析

本文的研究對象為2D12-70型雙作用對動式往復壓縮機，對氣閥故障進行研究，主要參數為：軸功率500 kW、排氣量70 m3/min、活塞行程240 mm、曲軸轉速496 r/min。模擬了彈簧失效、閥片斷裂和閥片缺口三種常見故障，在氣閥閥蓋處布置傳感器測定振動信號，采集正常和故障兩種振動信號，信號采樣頻率為50 kHz。設置了四種狀態：彈簧失效、閥片斷裂、閥片缺口以及正常狀態，每種狀態的樣本數取40個，四種狀態共計160個，而每個樣本的數據長度均為2 048。四種狀態的時域波形如圖6所示，

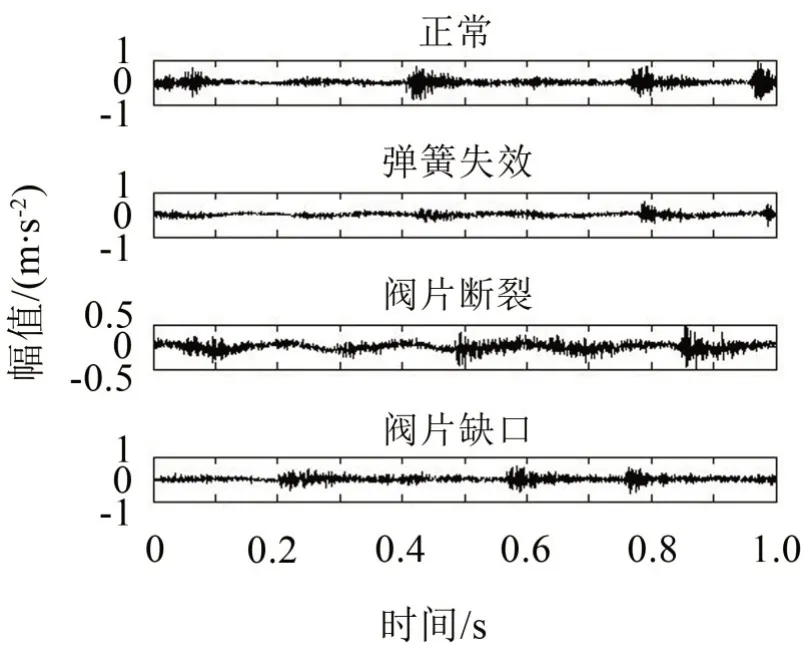
圖6 氣閥四種狀態振動信號的時域波形圖

計算所有樣本的SVMFE值，每種狀態在不同尺度因子下的SVMFE值如圖7所示。

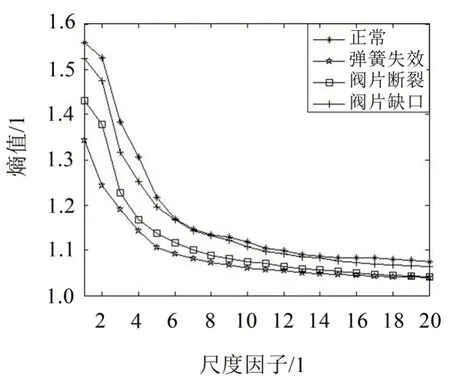
圖7 氣閥四種狀態振動信號的SVMFE值

由圖7 可以看出，四種狀態振動信號的SVMFE值隨尺度因子變化的趨勢大體相同，均是在第一到第六個尺度急速下降，之后緩慢下降趨于穩定。在大部分尺度上，四種信號的SVMFE 值的大小順序是：正常＞閥片缺口＞閥片斷裂＞彈簧失效。此外，在尺度因子較大時，四種狀態的SVMFE 值差別較小，還出現交叉和重疊的現象，如果將大尺度下的SVMFE值作為特征向量，雖然也能大體區分故障類型，但容易出現信息冗余，不利于狀態的分類識別，導致故障信息不能充分描述。結合圖7 的SVMFE值曲線，四種狀態的前五個尺度對應的SVMFE值區分明顯，故本文選取每種狀態的前五個尺度因子對應的SVMFE 值作為樣本的特征向量，并采用ELM對這些特征向量進行分類，以實現氣閥各種狀態的分類和識別。其中，ELM 的激活函數選Sigmoid 函數[15]，隱層神經元的數目設置為25。首先，從每個狀態下隨機抽取10個樣本作為訓練集，另外30個為測試集，具體信息如表1所示。其次，將訓練樣本輸入到ELM 中進行訓練。最后將測試樣本輸入到訓練好的ELM中進行識別，結果如圖8所示。

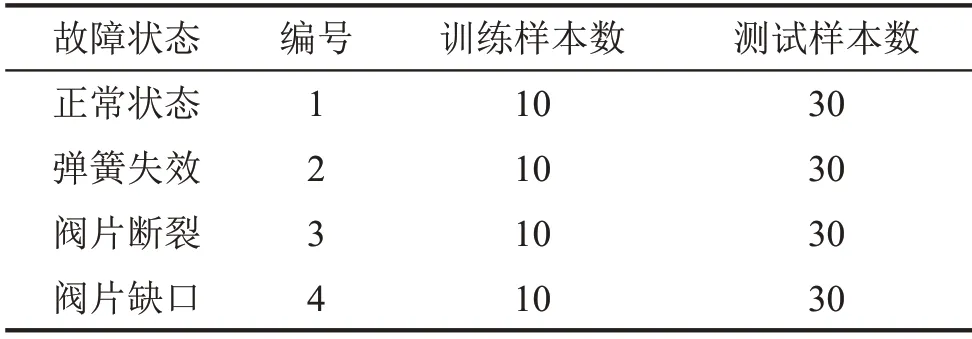
表1 訓練和測試實驗數據列表

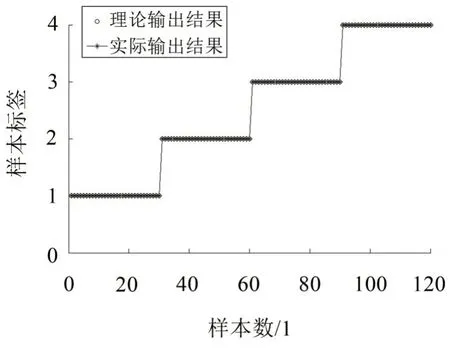
圖8 基于SVMFE與ELM的識別結果

由圖8 中可以看出，實際的輸出結果與理論結果完全相同，故障識別率為100%（120/120），說明本文所提方法能有效地識別氣閥的故障類型。

為了更好地驗證SVMFE 方法在特征提取上的優越性，將其與MFE 進行對比，計算160 個樣本的MFE值，取每種狀態前5尺度因子的MFE值作為特征向量，輸入到相同的ELM 分類器中訓練和測試，識別結果如圖9所示。

由圖9 可以看出，基于MFE 的特征提取方法總計有三個樣本被錯誤識別，一個彈簧失效被錯分為閥片斷裂、一個閥片斷裂被錯分為彈簧失效，一個閥片缺口被錯分為正常，故障識別率為97.5 %（117/120）。

SVMFE 與MFE 方法的故障識別結果如表2 所示，當氣閥為正常狀態時，兩種方法的故障識別率均為100%，說明二種方法都能夠準確地識別出氣閥的正常狀態；對于其他三種狀態，SVMFE 方法的故障識別率依然為100%，而MFE 方法出現錯分。結果表明SVMFE 方法無論是在整體上還是個別狀態的識別率均優于MFE 方法，驗證了SVMFE 方法在特征提取上的優越性。

為了研究訓練樣本數是否會對氣閥故障識別率的結果產生影響，選擇訓練樣本數為：5、10、15、20、25 和30 進行訓練，訓練和測試的數據與上文相同，故障識別結果如表3所示。

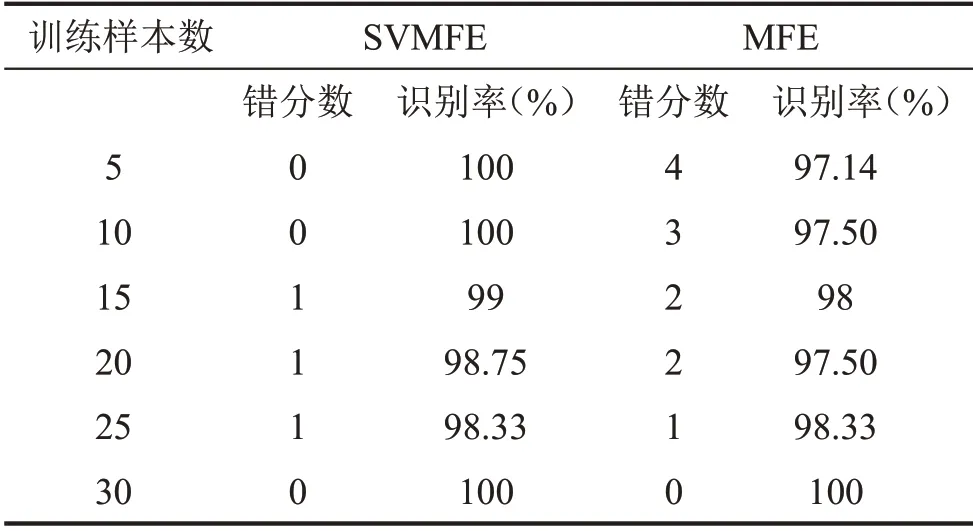
表3 不同訓練樣本數兩種方法的識別結果

通過在不同樣本數下，兩種方法的對比可以看出，SVMFE 方法在樣本數為5 和10 時，錯分數為0，識別率為100%，遠高于MFE方法；當樣本數逐漸增加時，SVMFE 方法出現錯分，識別率降低，而MFE方法的錯分數逐漸減少，故障識別率增高，當樣本數為25時，兩種方法的識別率相同，當樣本數為30時，兩種方法識別率為100%。說明無論訓練樣本數是多或者少，SVMFE方法的故障識別率均高于或者等于MFE的，表明基于SVMFE與ELM相結合的故障診斷方法更適用于訓練樣本小的往復壓縮機氣閥故障診斷。在大型設備中，往往故障信號采集很困難，訓練樣本數稀少，該方法能有效地解決小樣本的故障識別問題。

為了研究特征向量中熵值的數目是否會對氣閥故障識別率的結果產生影響，運用SVMFE 和MFE兩種方法計算尺度因子為2 到20 上的熵值，作為信號的特征向量用于氣閥故障診斷。訓練和測試的數據與上文相同。兩種方法在不同特征值數目下的故障識別率如圖10所示。

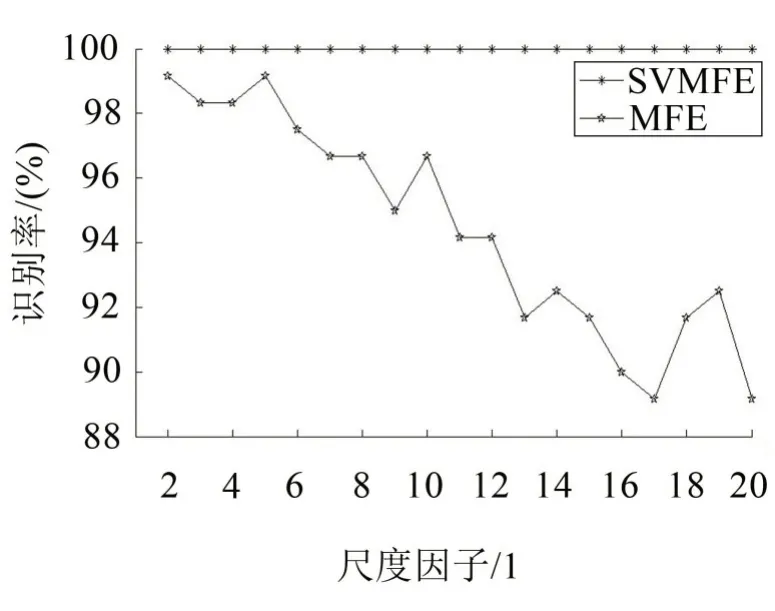
圖10 兩種方法的故障識別率對比

由圖中可以看出，從第2 到20 個尺度因子的熵值作為特征向量，故障識別率均為100%，說明基于SVMFE的特征提取方法，識別率不受特征向量中熵值數目的影響；而基于MFE 的特征提取方法，識別率明顯受特征向量中熵值數目的影響較大。這表明SVMFE 方法只需要較小的特征向量就能夠完整地反映出故障特征信息，從而有效地實現故障識別。

4 結語

本文提出了一種描述時間序列復雜程度的SVMFE算法，并將其與MFE對比，說明了本文方法的優越性。提出基于SVMFE與ELM的往復壓縮機氣閥故障診斷方法，通過分析氣閥四種狀態的實驗數據，將其與MFE對比，結果表明SVMFE方法在特征提取時誤差更小，結果更穩定，能夠全面地描述氣閥各種狀態的故障信息，同時基于SVMFE 與ELM的方法更適合于小訓練樣本數據，僅需要較小的特征向量就能夠完整地反映出氣閥的故障特征信息，且具有較高的故障識別率。綜上所述，SVMFE有效地解決了MFE在粗粒化計算中存在的問題，在表征故障特征方面有一定的優勢，希望能將它推廣到其他機械設備的故障診斷中。