基于最大相關峭度解卷積行星齒輪箱微弱故障診斷
劉 峰,任麗佳
(上海工程技術大學電子電氣工程學院,上海 201620)
行星齒輪箱被廣泛地應用于各種傳動系統中,例如:風力渦輪機、直升機、卡車等,其工作狀態正常與否會影響整個傳動系統的效率。當行星齒輪箱發生嚴重(晚期)故障時,振動信號表現出明顯的周期性沖擊,通過常規的時-頻分析手段即可診斷出。但是在實際工業環境中,往往要求對行星齒輪箱進行早期故障診斷,為機器決策維修提供充裕的時間。因此,行星齒輪箱進行微弱故障特征的提取,識別出行星齒輪箱故障狀態,對保證行星齒輪箱的可靠性運行起到了至關重要的作用。怎樣及時地發現行星齒輪箱的微弱故障特征,避免造成重大事故一直是國內外研究的熱點。
近些年來,微弱故障特征提取一直是研究的重點和難點[1]。可用于微弱故障特征檢測和診斷方法有許多種,其中振動信號分析最為廣泛[2-3]。譜峭度[4]、最小熵解卷積[5]、經驗模態分解[6]、奇異值分解[7]等方法分別對傳感器收集到的振動信號進行處理,分析提取出的振動沖擊信號,并且可以提取出微弱故障特征,診斷行星齒輪箱故障狀態。為了能夠更好、更準確地識別出微弱故障,有時候也將上面的兩種或幾種方法結合起來[8-9]。
本文首先對收集到的行星齒輪箱信號進行烈度因子分析,通過烈度可以識別出處于不同故障狀態的行星齒輪箱。然后對處于微弱故障狀態中的信號進行局部均值分解(LMD),根據各個PF分量的快速譜峭度圖,選取含有豐富沖擊分量的PF,對信號進行重構。最后MCKD算法對重構信號進行處理,之后對處理過的信號進行包絡譜分析。通過分析包絡譜譜線,可以準確識別出行星齒輪箱所處的故障狀態。
1 特征提取
1.1 烈度因子
烈度因子可以反映出行星齒輪箱運行狀況的真實狀態,而且受外界干擾的影響小,國內外很多專家經常把振動烈度當作機器的振動標準。振動烈度定義為頻率10 Hz~1 000 Hz 范圍內的振動速度的均方值,其可以準確反映行星齒輪箱運行狀態的特征因子。烈度定義為:對于收集到離散振動速度信號v(t),假定振動信號有N個點,計算公式如下:
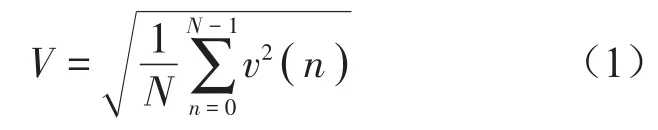
行星齒輪箱的振動程度可以由振動烈度反映出來,通過振動烈度可以反映出行星齒輪箱所受的不同故障程度。
1.2 局部均值分解(LMD)
LMD 是一種自適應非平穩信號的處理方法,非常適合處理非線性,非平穩的信號。LMD方法的創新點在于將一個單分量的調幅-調頻信號看成是其本身的包絡信號和一個純調頻信號的乘積,通過定義局部均值函數和包絡估計函數,在對原始信號不斷平滑的過程中獲得瞬時頻率,然后將純調頻信號和包絡信號相乘便可以得到一個PF 分量,每個PF分量實際上是一個單分量的調幅-調頻信號,這樣使得LMD方法非常適合于處理非平穩和非線性信號。
當行星齒輪箱在微弱故障狀態下運行時,周期性沖擊分量非常小,通常淹沒在諧波分量和解調分量中。為了去除這些干擾分量,本文用LMD對處于微弱故障狀態的振動信號進行分層,然后用快速譜峭度圖選取含有豐富沖擊分量的層數進行信號重構,為下文求最大化相關峭度奠定基礎。
2 最大相關峭度解卷積(MCKD)
峭度是無量綱參數,它與機械的轉速、尺寸、載荷等無關,對單一沖擊信號特別敏感,特別適合于早期故障的診斷。但是對于混雜著周期性故障沖擊分量的旋轉機械信號,峭度不能取得比較好的效果。由于周期性故障分量的增加,峭度將會逐漸變小,最終與正常狀態的峭度值相等,識別效果不夠理想。MCKD 算法對處理這類信號有比較好的效果,可以突出信號中被諧波和噪聲掩蓋的周期性沖擊分量,提高振動信號的信噪比。
為了提取序列中的周期性沖擊分量,本文提出了相關峭度,周期為T,時延階為M的相關峭度在式(2)中表示:
液料比為15∶1、20∶1、25∶1、30∶1、35∶1 mL/g時,實驗結果如圖6所示.液料比小于25∶1 mL/g時,溶劑越多,多糖得率越高;液料比大于25∶1 mL/g時,溶劑越多,多糖得率越低;當液料比達25∶1 mL/g時,得率達最大值.這是因為:更多的溶劑能溶解更多的多糖,但也會導致果膠酶濃度降低,使酶活性降低[20,22].因此,最佳液料比為25∶1 mL/g.
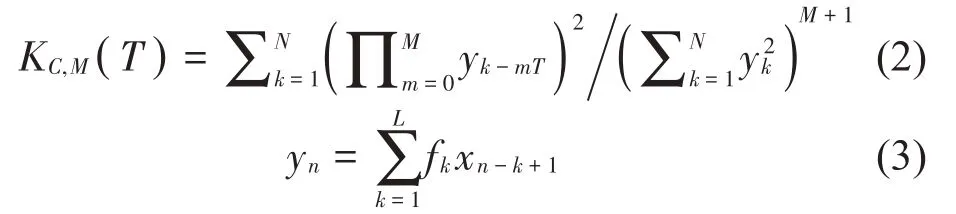
式中:N是信號中采樣點數;M是移位的周期個數;T是沖擊信號感興趣的周期。當M=1,T=0時候,相關峭度變為峭度。如圖1所示,相關峭度與峭度相比,對于單個沖擊信號,峭度發生明顯變化。但是當信號中周期性分量增加,相關峭度值會變大,峭度值會變小。通過最大化相關峭度來提取周期性故障脈沖,可以還原出微弱故障產生的周期性沖擊分量,提高感興趣周期性脈沖所占比重,增加行星齒輪箱的微弱故障特征識別率。
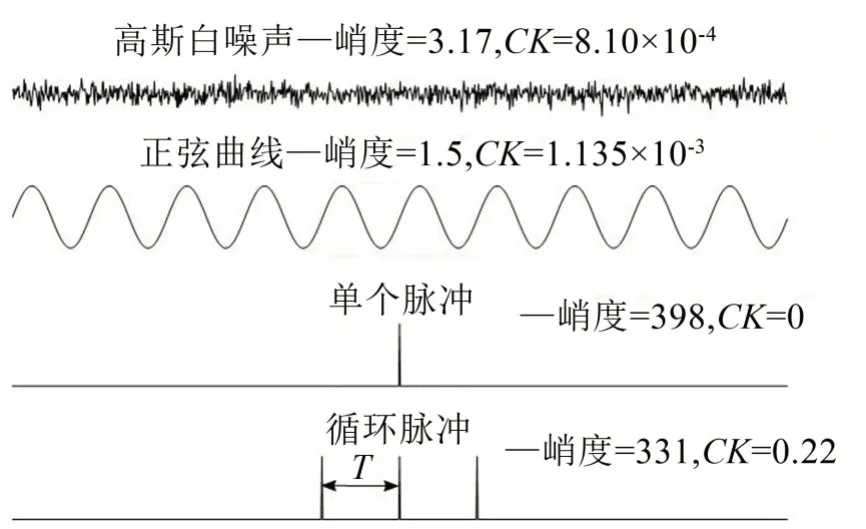
圖1 四種信號的峭度和相關峭度值
在MCKD算法中,通過最優化設計解卷積濾波器f,這樣做的目的是得到最大化的相關峭度KC,M(T)值,如式(4)所示:
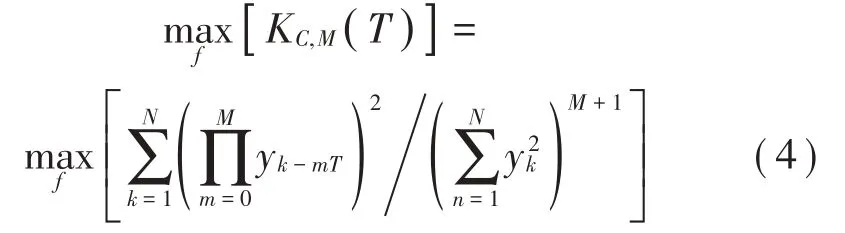
對上式(4)推導,可得到MCKD 最優濾波器系數:
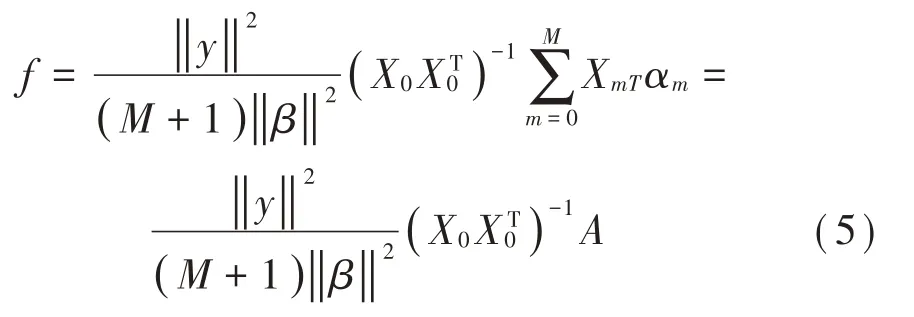
在式(5)中:f=[f1,f2,…,fL]T,其中T為轉置;
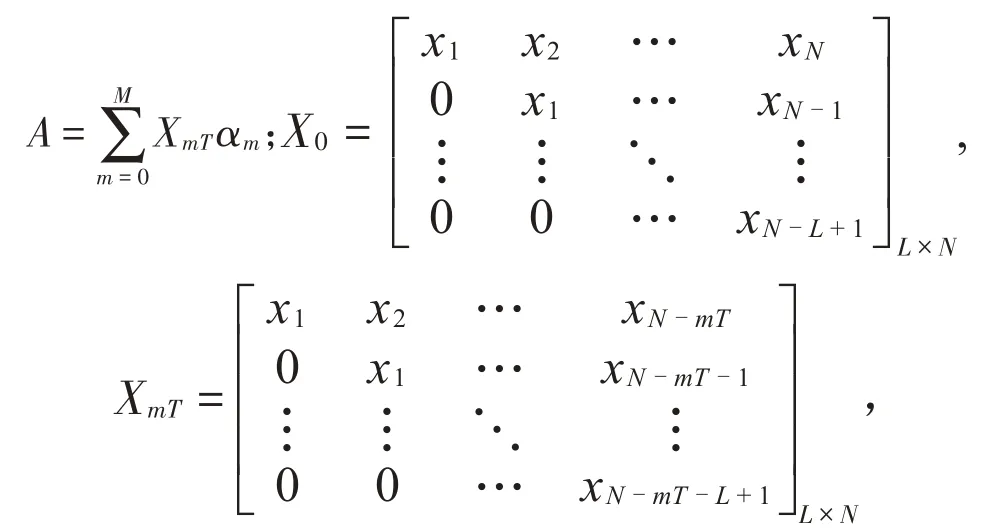
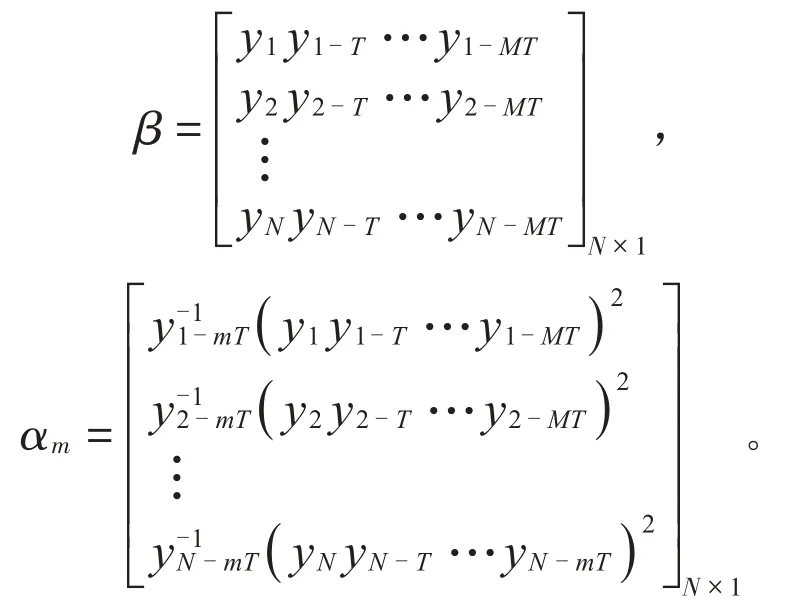
MCKD算法的流程圖如圖2所示。
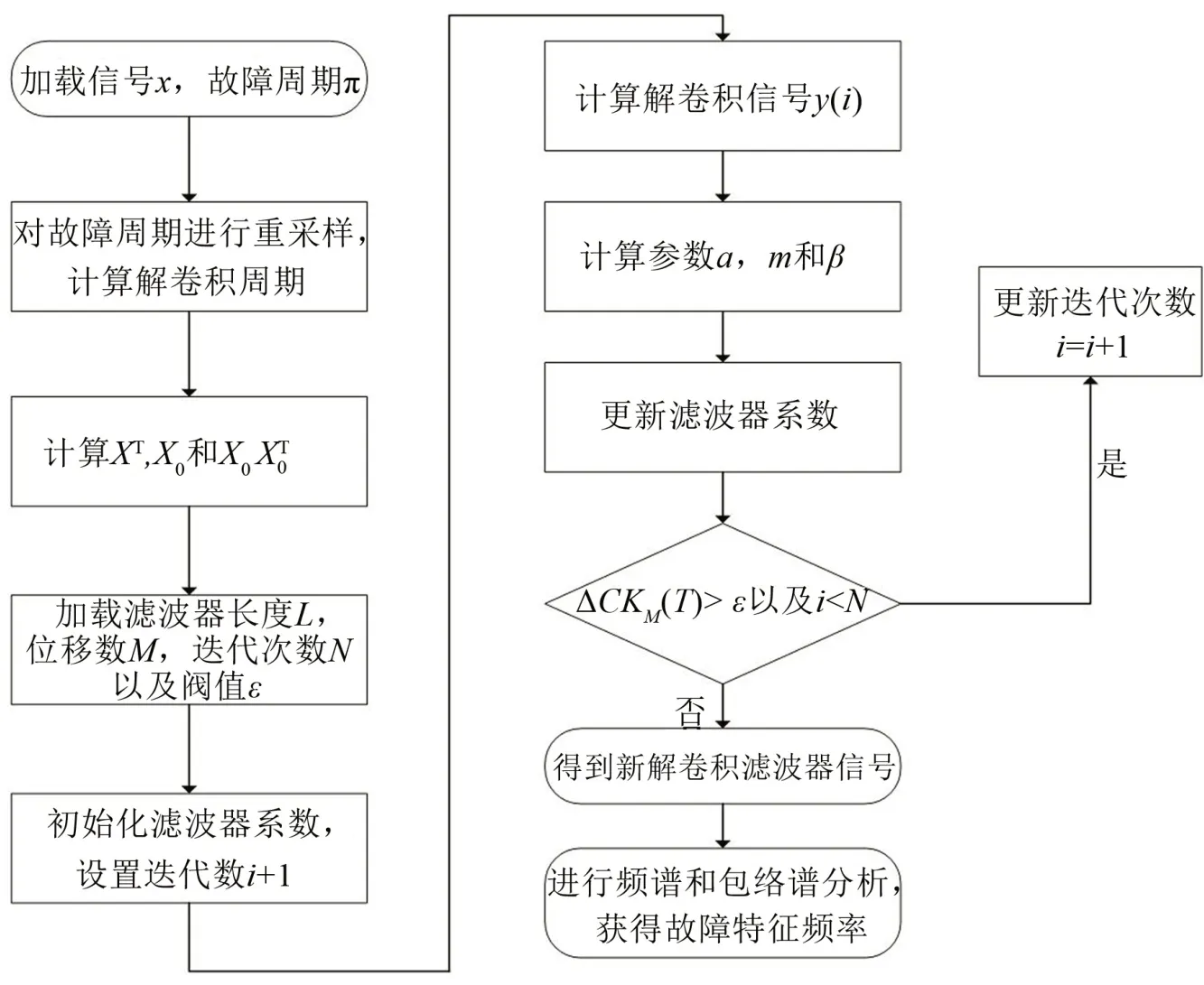
圖2 最大相關峭度解卷積流程圖
3 實驗驗證
本文收集到的振動信號來自傳動系統診斷綜合平臺(DDS)。該綜合平臺的裝置實物圖如圖3所示。

圖3 傳動系統診斷綜合平臺(DDS)實物圖
圖中展示的實驗平臺是由一個2級平行軸齒輪箱,一個2 級行星齒輪箱,變頻器,電機,聯軸器,制動器和加速度傳感器組成。其中故障齒輪是第二級傳動的太陽輪,其他一切完好無損,沒有任何故障。行星齒輪箱中各個齒輪分布情況在表(1)。在本實驗中,加速度傳感器用于收集振動信號,放于太陽輪有故障的行星齒輪箱頂部,實驗中輸入的轉速為40 r/s,采樣頻率為3 200 Hz,負載25.2 N·m。
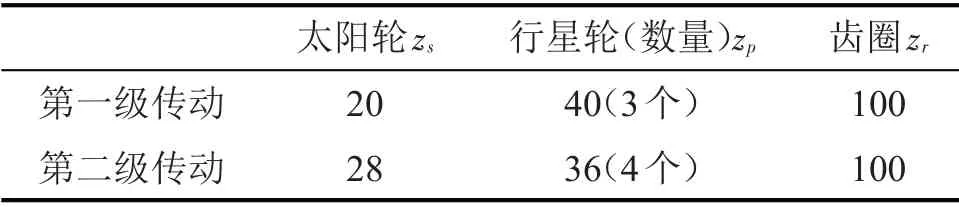
表1 行星齒輪箱中各齒輪齒數
圖4中表示了行星齒輪箱振動信號時-頻圖。整個運行時間段看不出有規律的沖擊特征;頻譜中也沒有明顯的故障特征頻率成分,只有一些突出的干擾成分和噪聲頻率。
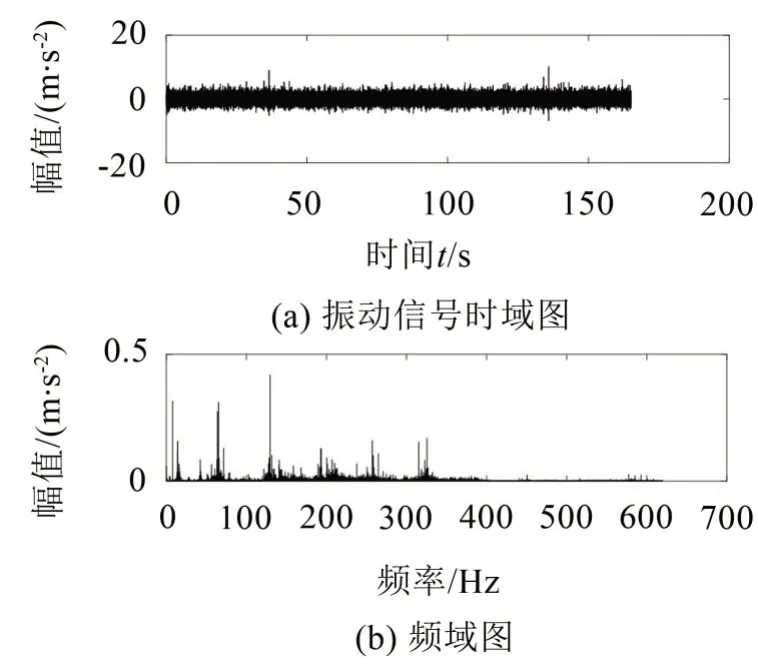
圖4 行星齒輪箱振動信號
為了提取出行星齒輪箱微弱狀態特征,將MCKD算法應用到收集的振動信號中。
為了識別行星齒輪箱的不同狀態。把收集到的振動信號每100 個點求一個烈度,然后得到一系列烈度值,如圖5所示。根據信號中一系列的烈度值,可以看出在40 和80 時刻,烈度發生階躍性變化,表明行星齒輪箱狀態發生了變化,40時刻行星齒輪箱進入微弱故障狀態,80時刻行星齒輪箱進入嚴重故障時刻。
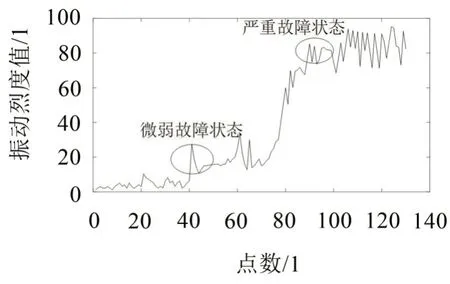
圖5 行星齒輪箱不同時刻烈度圖
選取處于微弱階段振動信號,用LMD算法對選取出的信號進行預處理。LMD 把行星齒輪箱微弱階段信號分解成有限PF分量之和,微弱故障特征信號特征都展現在各個PF 分量之中,如圖6所示。然后對每一個PF分量進行快速譜峭度分析,得到關于各個PF 分量的快速譜峭度圖,如圖7所示。通過快速譜峭度圖可以看出PF1和PF2中包含的故障信息和沖擊成分比較豐富。選取PF1和PF2分量,對振動信號進行重構。信號重組可以更有效地保留原始信號中更多的故障信息,獲得信噪比更高的故障特征信號,為MCKD處理信號奠定基礎。
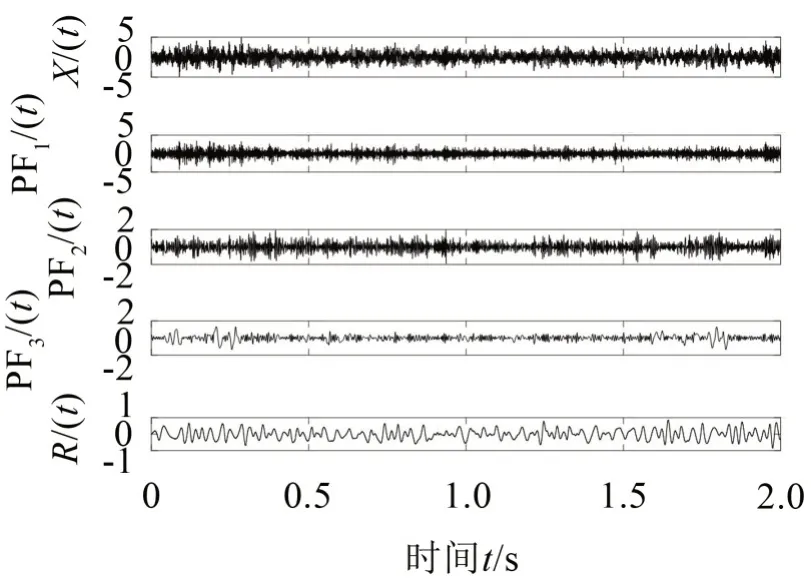
圖6 微弱故障狀態下振動信號LMD分解
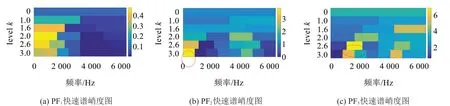
圖7 各PF分量快速譜峭度圖
MCKD可以提取出微弱的周期性沖擊成分。但其降噪效果受參數的影響較大,尤其是位移數M,濾波器長度L。對于位移數M,M越大提取的信息越完整,一般情況下,令M≤7。濾波器長度L影響計算的時間,一般把L設定為一倍到兩倍的解卷積周期。對于DDS 傳動系統,MCKD 算法中的L=400,M=7。對重構信號進行MCKD算法處理,增加行星齒輪的早期故障沖擊信號。最后對MCKD 處理后的信號進行包絡譜分析。為了對比分析,同時對重構信號進行最小熵解卷積(MED)處理,圖8(a)為經過MED處理后的振動信號圖,圖8(b)為經過MED算法后的包絡譜分析。將經過MED和MCKD算法處理過的振動信號的包絡譜進行比較,可以看出經過MCKD處理過的振動信號,隱藏在重構信號中的周期性沖擊特征明顯地展示出來,可以將振動信號中的噪聲成分有效地濾除。重組的振動信號經MCKD處理,然后通過包絡譜分析。圖9(b)中譜線在1倍頻、2倍頻、3倍頻、4倍頻和5倍頻處,有明顯的譜峰,可以清晰地識別出行星齒輪箱處于微弱故障狀態。
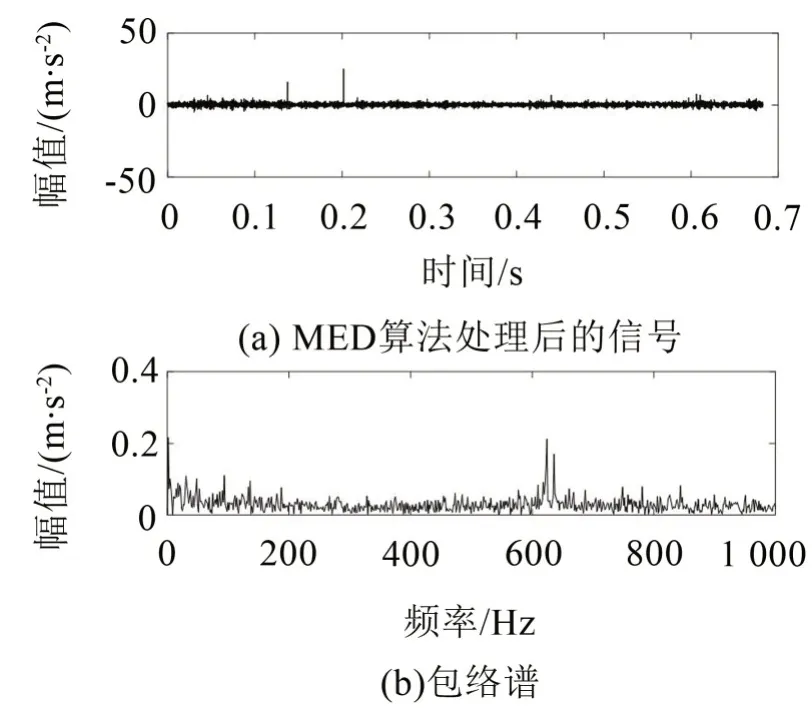
圖8 重構信號MED信號圖和包絡譜
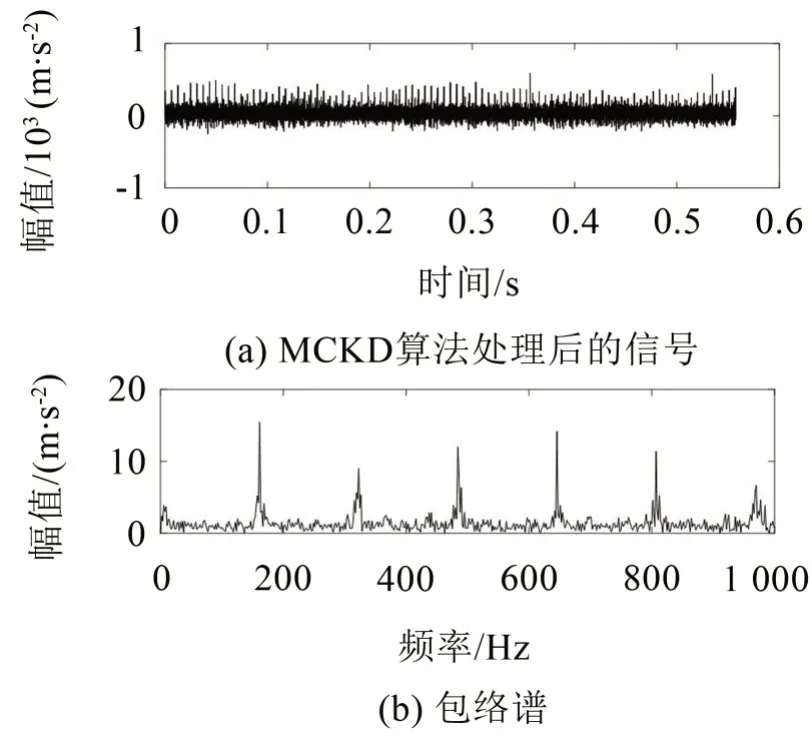
圖9 重構信號MCKD信號圖和包絡譜
4 結語
本文在相關峭度的基礎上,將MCKD算法應用于行星齒輪箱微弱故障識別中,有效地解決了行星齒輪箱微弱故障特征難以提取的問題,提高了微弱故障識別的準確性和魯棒性。最后將該方法應用于DDS平臺收集到的振動信號中,取得了不錯的效果。通過實驗,得出下面幾點結論:
(1)通過求行星齒輪箱不同時刻的烈度,判別行星齒輪箱所處不同健康狀態。
(2)LMD 分解可以有效地克服模態混疊的問題,非常適合于分析行星齒輪箱處于微弱狀態的信號。根據對各個PF 分量進行快速譜峭度圖重構信號,使重構信號中含有更多的沖擊分量。
(3)重構信號進行MCKD算法可以提高信號中的周期性沖擊分量,克服了MED只對局部沖擊信號敏感的缺陷;提取的故障特征頻率幅值更大,識別率更準確,增加了工程應用價值。此外該方法也適用于其他旋轉機械(例如軸承,其他型號齒輪箱等)的微弱故障提取。

