地下綜合交通樞紐上蓋建筑環境振動預測評估
——以北京城市副中心站綜合交通樞紐為例

張登科，趙 磊，劉 文，陳旭超，何遠鵬，成 功

（1.北京京投交通樞紐投資有限公司，北京 100101；2.北京市市政工程設計研究總院有限公司，北京 100082；3.西南交通大學牽引動力國家重點實驗室，成都 610031）

中國地鐵建設在進入21世紀以來突飛猛進，運營里程顯著增加，但想要大力發展地鐵項目，僅靠政府財政往往不能平衡，因此，在如何解決地鐵建設資金問題的大背景下，較為成熟的“地鐵+上蓋物業”，即：以公共交通為導向的城市開發模式（TOD）模式逐漸受到推崇。同時，地下綜合交通樞紐在織補城市、創造高品質公共空間、集約用地以及消除鐵路分隔等方面有著天然優勢[1]。交通樞紐依托軌道交通設置于地下，樞紐上方土地綜合開發利用，形成“站城一體”的樞紐開發模式。

然而TOD區域線路交匯越多、上蓋建筑形式復雜，往往容易導致振動和噪聲更加突出，對地下樞紐的舒適換乘體驗、地上高品質業態的開發造成了不利影響。例如地下高鐵站靠近城市的功能中心，地上建筑也更為密集且靠近鐵路線路，甚至和車站結構共用基礎；此外一定數量的列車在車站正線以中低速穿行，輪軌激勵振動會直接作用于建筑結構并在其中傳播。如果處理不當，未來高強度的鐵路運輸（城際鐵路、地鐵）會給該區域帶來大量的建筑環境振動和結構噪聲問題，影響該區域人民的工作、居住、身體健康及出行體驗，因此在工程的設計期便有必要對這類工況開展環境振動及結構噪聲的預測評估研究，使得在項目前期將減振降噪措施有針對性地考慮進規劃，一方面滿足相關規范，另一方面保證建筑的使用品質。

針對地鐵引起的車站與上蓋建筑的振動與噪聲問題，國內外學者從實測分析與數值仿真兩個角度展開了研究。雷曉燕等[2]對某一大型綜合交通樞紐車站的站房振動進行了實測，分析得到了不同樓層的振動主頻。周凌宇等[3]對地鐵車站內站廳層的振動與噪聲進行了測試，并對振動與噪聲超標的房間加裝吸聲板、吸聲棉、與減振墊，測試了其減振降噪效果。謝偉平等[4]通過實測與有限元模擬，計算分析了一棟高11 層的上蓋建筑的振動響應，結果表明：上蓋建筑的振動成分由列車激勵荷載決定，集中在40 Hz 附近；建筑內鉛垂向的Z 振級隨樓層上升，呈現先降低后增大的趨勢。鄒超[5]對地鐵車輛段附近的多種上蓋建筑的振動進行了實測，發現垂向振動在上蓋建筑的頂層有放大效應；并研究了隔振溝填充物的優化設計方案，結果表明在建筑物振動的主要頻段內，空溝的隔振效果最好。王一干等[6]對車輛段與上蓋建筑的振動噪聲進行了實測，研究了地鐵引起的建筑振動與二次結構噪聲，發現兩者在頻域上具有高度的一致性，驗證了根據樓板振動計算房屋二次噪聲的經驗公式。Guo 等[7]對一座三層地鐵停車場的振動進行研究，測量了振動加速度，并進行了數值模擬，提出垂向振動比橫向振動顯著，是主要的評價指標。Yang等[8]對一大型車站樞紐結構的振動進行了有限元計算，通過預測分析發現對建筑物基礎安裝鋼彈簧浮置板能取得較好的隔振效果。

目前的研究更多集中于軌道交通車站的環境振動或地鐵在隧道中下穿通過引起的建筑物振動，對軌道直接落于建筑物樓板的工況研究較少，同時國內存在著幾個相關標準對城市區域的環境振動和二次結構噪聲進行規范，需要針對這些情況開展預測研究。北京城市副中心站綜合交通樞紐位于北京市通州區0101街區，樞紐范圍三條國鐵線路及三條地鐵線路交匯，交通樞紐依托城際鐵路設置于地下，樞紐上方采用共構方式建設現代化城市綜合體，城市副中心站有創造高品質公共空間開發需求。因此，本文依托北京城市副中心站綜合交通樞紐工程，以模型計算的方法為基礎，對國內現行的評價標準開展振動及噪聲的綜合對比，研究樞紐上部建筑的振動特性，計算并比較不同軌道減振措施對環境振動及二次結構噪聲的影響，對提升綜合交通樞紐開發品質有重要意義。

1 模型預測方法

1.1 車輛模型

采用多剛體半車模型，包含車體、轉向架、輪對以及一二系懸掛。列車的振動微分方程為：

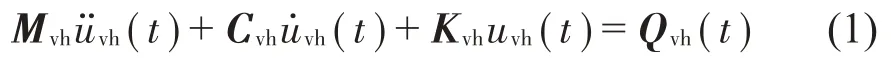
式（1）中物理量含義如下：

Mvh——列車質量矩陣；Cvh——列車阻尼矩陣；

Kvh——列車剛度矩陣。

Qvh（t）——列車等效載荷向量；uvh（t）——列車位移向量。

1.2 軌道模型

軌道系統從上至下依次為鋼軌，軌道扣件，軌道板，減振墊，底座板。鋼軌與軌道板模擬為連續支撐的歐拉梁模型，扣件與減振墊考慮為阻尼彈簧，底座板考慮為剛性。在模型中，單個扣件的節點剛度除以扣件間距，得到每延米的剛度作為計算值。

軌道方程在波數域有如下形式：

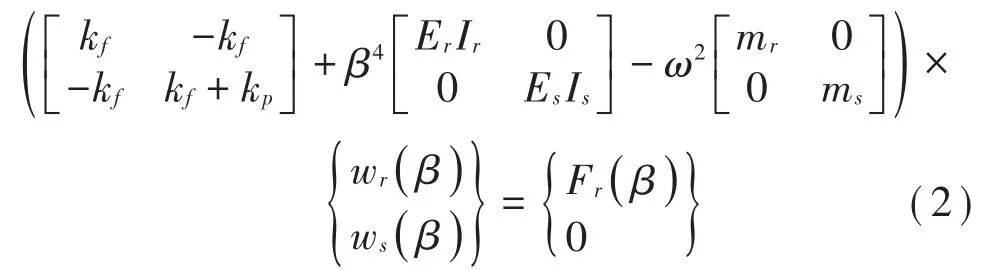
式（2）中：kf為扣件剛度，kp為減振墊剛度，ErIr為鋼軌的彎曲剛度，EsIs為軌道板的彎曲剛度，mr為鋼軌的質量，ms為軌道板的質量，wr為鋼軌的垂向位移，ws為軌道板的垂向位移。

1.3 輪軌相互作用模型

輪軌之間的動態相互作用力是系統的激勵源，對于200 Hz以內的輪軌系統的振動，長波不平順的幅值引起的振動占主導地位。本文采用文獻中提出的基于軌道垂向不平順的垂向激勵模型，通過該模型進行計算，得到輪軌系統對應于不同波長的單位粗糙度下的輪軌力響應，再結合軌道不平順功率譜，即可得到系統的輸入激勵。

輪軌耦合模型如圖1所示。輪對與鋼軌之間為赫茲接觸，假設輪對與鋼軌不發生分離，可得輪軌之間位移匹配方程：

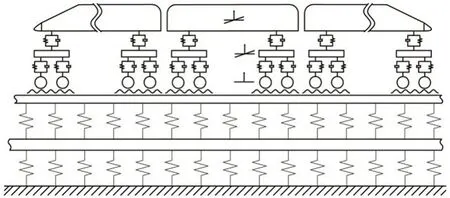
圖1 垂向輪軌耦合模型

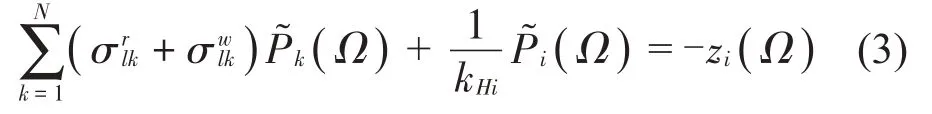
式中：σrlk表示鋼軌上第l和k兩個輪軌接觸點之間的位移傳遞函數，可通過對式（2）進行傅里葉逆變換求得。σwlk表示車輛中第l 和k個輪對之間的位移傳遞函數，可通過列車系統的柔度矩陣進行計算。已知粗糙度幅值，可以計算得到輪軌力幅值

1.4 樞紐-土層有限元模型

由于隧道-大地結構具有長度方向無限長，且橫截面大的特性，如果用三維數值模型對其進行計算會消耗大量的算力。然而，列車長度較長，故可將列車與隧道土層的相互作用看作平面應變問題，利用二維有限元模型進行簡化計算。有限元模型如圖2所示。

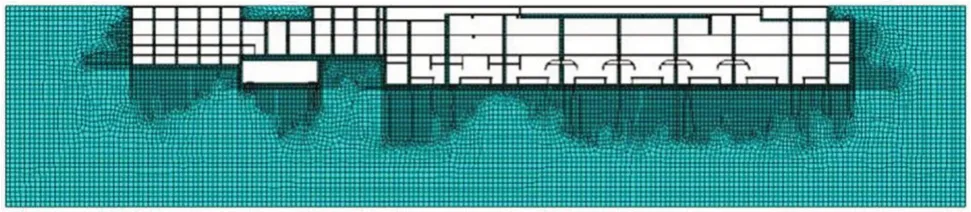
圖2 樞紐-土層有限元模型

1.5 建筑有限元模型

由于建筑物相對于車站體量較小，因此可以采用子結構的方式進行建模，在計算地表振動時不考慮房屋結構的耦合。以樞紐范圍內一棟27 層公寓為例開展室內振動及二次結構噪聲規律研究。公寓建筑高度100 m，鋼筋混凝土框架剪力墻結構，房屋結構模型如圖3 所示。其中，有限元模型主梁和側梁由BEAM188 單元建立復合梁，樓板和承重墻等由SHELL63 單元建立，混凝土彈性模量為3.6×1010Pa，泊松比為0.2，密度為2 400 kg/m3，損失因子為0.1。鋼材彈性模量為2.1×1011Pa，泊松比為0.3，密度為7 800 kg/m3，損失因子為0.01。

圖3 建筑三維有限元模型

1.6 模型預測方法驗證

為驗證計算方法的可靠性和有效性，選取北京地鐵15 號線現場測試數據與文中的模型預測方法進行對比。測試斷面情況：測試點布設在直線段上如圖4至圖5所示；60 kg/m鋼軌，材質為U71Mn；道床為短枕式整體道床，混凝土強度等級為C35，圓形隧道地段道床斷面寬為2 300 mm，道床設兩側水溝，每側水溝寬為300 mm（圓形隧道及U 形槽地段水溝延至結構邊墻）；采用DTⅥ2無擋肩彈性分開式扣件，扣件垂直靜剛度為20 kN / mm～40 kN/mm，一組扣件的防爬阻力不小于11.5 kN，軌距調整量為+8 mm、-12 mm，水平調整量一般為30 mm；扣件布置間距均為600 mm，軌面埋深20.6 m；根據實測數據表明，列車運行速度平均值為70.01 km/h。測試內容包括：輪軌垂、橫向力；鋼軌垂、橫向位移和軌枕垂向位移；鋼軌、軌枕、道床、隧道壁加速度。

圖4 北京地鐵15號線測試現場

圖5 測試現場傳感器布置圖

地鐵車輛為B型車，車輛6節編組（4M+2T），軸距2.2米，軸重不大于14噸。考慮地鐵軌道狀態，將測得的短波不平順和美國6級譜的長波段得到聯合粗糙度譜，如圖6所示。

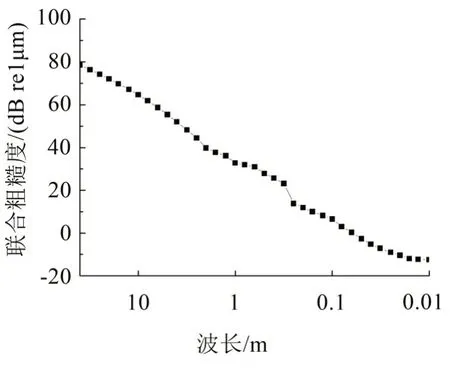
圖6 聯合不平順功率譜

采用上文方法建立測試斷面有限元模型，車輛計算參數如表1 所示，隧道埋深為17.1 m，內徑2.7 m，計算參數如表2 所示。讀取模型隧道壁1.2 m 位置1/3 倍頻程加速度振級，并與測試數據進行對比（測試數據按照測試標準《GBT19846-2005 機械振動列車通過時引起鐵路隧道內部振動的測量》測試獲得）。選取線路運營高峰時段（上午8 時、中午12時、晚上8時）各10組（共30組）測試數據進行分析。

表1 車輛模型參數

表2 隧道-大地模型參數

考慮車速為70 km/h 計算得到整個模型的振動響應，同時與實測數據進行對比，結果如圖7 所示，在8 Hz～80 Hz范圍內，隧道壁振動加速度級的模擬值和實測值的絕對誤差不超過5 dB。考慮到問題的復雜性，我們認為模型和方法基本能反映實測情況，可用于本項目的研究。

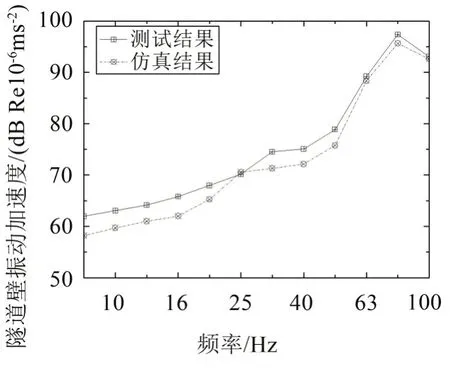
圖7 仿真模型對比驗證

2 上蓋建筑環境振動及結構噪聲評價標準橫向對比

利用上文模型計算得到樞紐-土層的振動加速度，將其施加在建筑底部，便可計算建筑物的振動及二次結構噪聲。

2.1 環境振動評價標準對比

對交通樞紐進行環境振動影響評價，應結合樞紐功能定位、地上建筑業態布局，以及樞紐所在地環境功能區劃選擇適當的振動評價標準，而目前常用的振動評價標準有GB10070-1988[9]和JGJ/T170-2009[10]。樞紐上蓋建筑的功能定位較為豐富（具有商業、公寓和辦公等功能），因此將其歸類為居住、商業混合區、商業中心區，同時該交通樞紐的上蓋建筑和地下車站為一個整體，建筑物室外0.5 m的測點位于車站混凝土板上方，和室內一樓的振動差異較小，本節的評價敏感點都位于室內房屋的中點。

圖8 給出了基于兩個振動評價標準：GB 10070-1988和JGJ/T170-2009得到的該建筑不同樓層的Z振級。

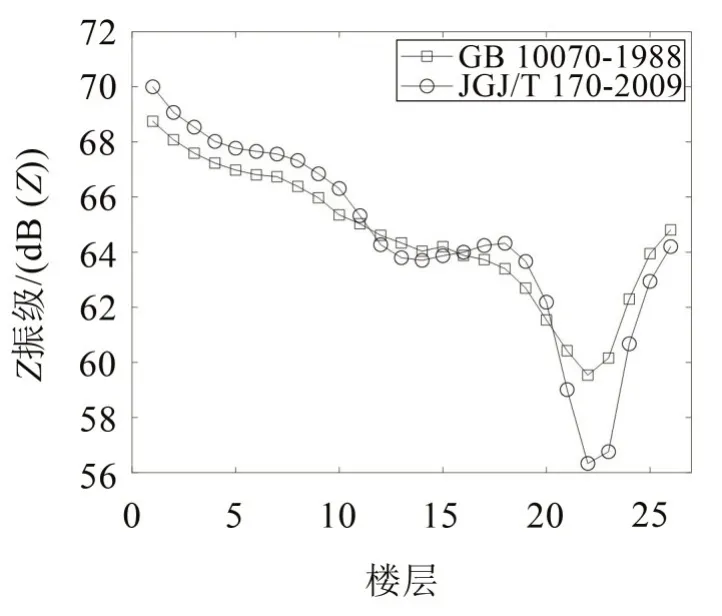
圖8 兩個振動評價標準得到的不同樓層Z振級

圖中可以看到：

（1）隨著樓層的增加，Z振級總體隨著樓層的增加而減小，在頂層附近會出現增大的現象，1樓和26樓的三分之一倍頻分頻振級（未計權）對比如圖9所示，可以看到雖然頂樓相比于底層的31.5 Hz以上的高頻振動得到了衰減，但頂樓在10 Hz 以下的低頻振動卻會放大，該頻率來自該建筑本身的振動模態；

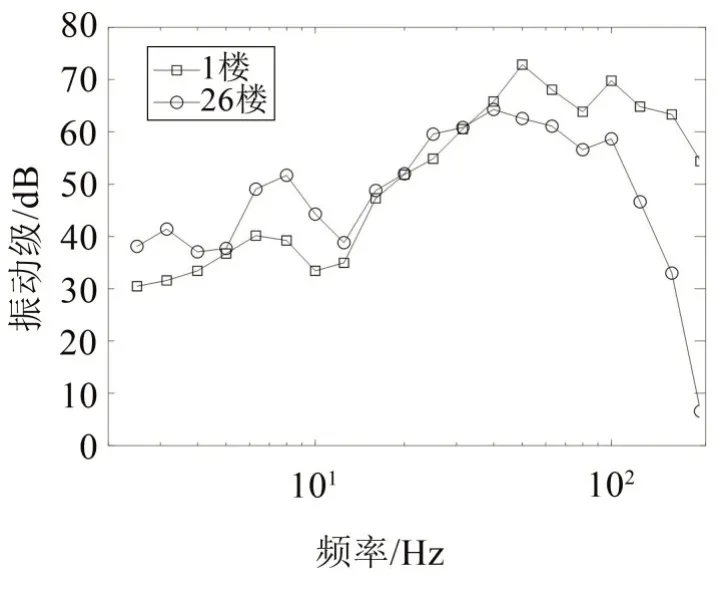
圖9 未記權振動級

（2）兩個振動評價標準給出的Z 振級在不同樓層顯示出一定的差異性，大小和差異幅值在不同樓層也并不相同。10 層以下的樓層，JGJ/T170-2009得到的Z 振級要高于GB10070-1988 得到的Z 振級，其差異值可以達到1 dB。由于分頻計權曲線的不同，兩個標準的計權曲線如圖8所示，可以看到兩個標準的計權曲線在10 Hz 以下差異較小，而在該頻率以上，兩者的差異可以達到5 dB 以上，即經過GB10070-1988 計權的10 Hz 以上分頻振動要遠低于JGJ/T170-2009計權得到的分頻振動；

（3）在20 層以上更高樓層，GB10070-1988 的振級卻要高于JGJ/T170-2009 的振級，這主要來自于評價量的不同，50 Hz以上頻帶的振動隨著頻率的增加而快速衰減，而其他頻帶衰減較小（如圖9 所示），使得分頻最大的振動（JGJ/T170-2009）在總的等效振動（GB10070-1988）所占比例下降；

（4）對于該高層建筑而言，10 層以下的振動仍是振動最容易超標的樓層，因此，采用JGJ/T170-2009得到的評價量要更為安全，同時由表1和表2可以看到，雖然兩個評價標準在工業集中區和交通干線兩側區域的限值相同，但是在居住、商業混合區、商業中心區—本高層建筑適用的區域，JGJ/T170-2009 的限值要低于GB10070-1988 限值5 dB（JGJ/T170-2009 規定限值標準為70 dB、67 dB，GB 10070-1988規定限值標準為75 dB、72 dB），加上因為評價量不同引起的1 dB差異，如果評價結果剛好滿足GB10070-1988的限值，但卻可能會超過JGJ、T170-2009的限值6 dB。

進一步對比不同樓層相同位置的頻譜特性，對1樓及26樓未計權振動級進行對比分析，如圖9所示。可以看到：隨著樓層增加，對于高頻振動（30 Hz 以上），有一定的衰減作用，但是對于低頻（30 Hz 以下），由于房屋結構類似于懸臂梁，在端部其低頻振動可能會被放大，因此對于高層房屋結構應注意低層不超標但是高層超標的現象。對比兩個振動評價標準（GB10070-1988和JGJ/T170-2009）在振動計權上的區別，標準中規定的振動分頻計權曲線如圖10所示。

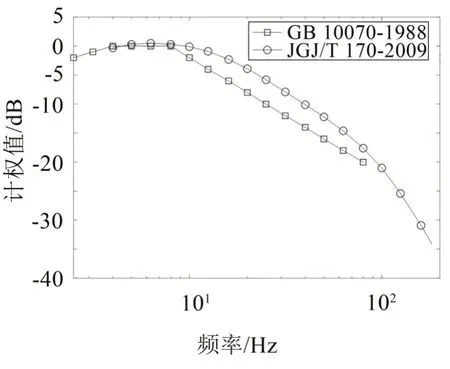
圖10 不同標準的振動分頻計權曲線

可以看到：GB10070-1988 的計權值要小于JGJ/T170-2009，在相同條件下，JGJ/T170-2009的振動加速度級比GB10070-1988 大，因此根據JGJ/T170-2009計算結果更易超標。

根據VGG-16網絡中卷積層的特點,以SeLU作為激活函數的ResNet,神經網絡層的解決率和深度值如表1和表2所示。

2.2 結構噪聲評價標準對比

由于建筑結構振動基本上均能滿足標準要求，因此參考HJ453-2018[11]規定對建筑結構二次結構噪聲進行評估。

基于兩個結構噪聲評價標準（GB/T50355-2018[12]和JGJ/T170-2009）得到的該建筑不同樓層的聲壓評價值如圖11所示，圖中虛線代表兩個標準的限值，由圖9 可知軌道交通引起的該建筑物結構振動能量主要分布在1/1 倍頻中的63 Hz 中心頻帶處，這里只對63 Hz頻帶進行分析。

圖11（a）至圖11（b）中對比可知，基于JGJ/T170-2009 進行評價，除1、2 層其他樓層的結構噪聲都可以滿足限值要求，而基于GB/T 50355-2018進行評價，其63 Hz 倍頻程的等效聲壓級在大部分樓層都有超標的風險，這是因為雖然后者標準的限值比前者高22 dB，但是由于后者標準不對聲壓進行A計權（對應50 Hz三分之一倍頻的記權值為-30 dB），因此63 Hz 頻帶的結構噪聲仍有較大的超標風險。從標準角度，二次結構噪聲的超標量大于環境振動。需要注意的是，后者的標準只是針對住宅，在評價商、住兩用的公寓時，后者的適用性需要得到進一步的探討。

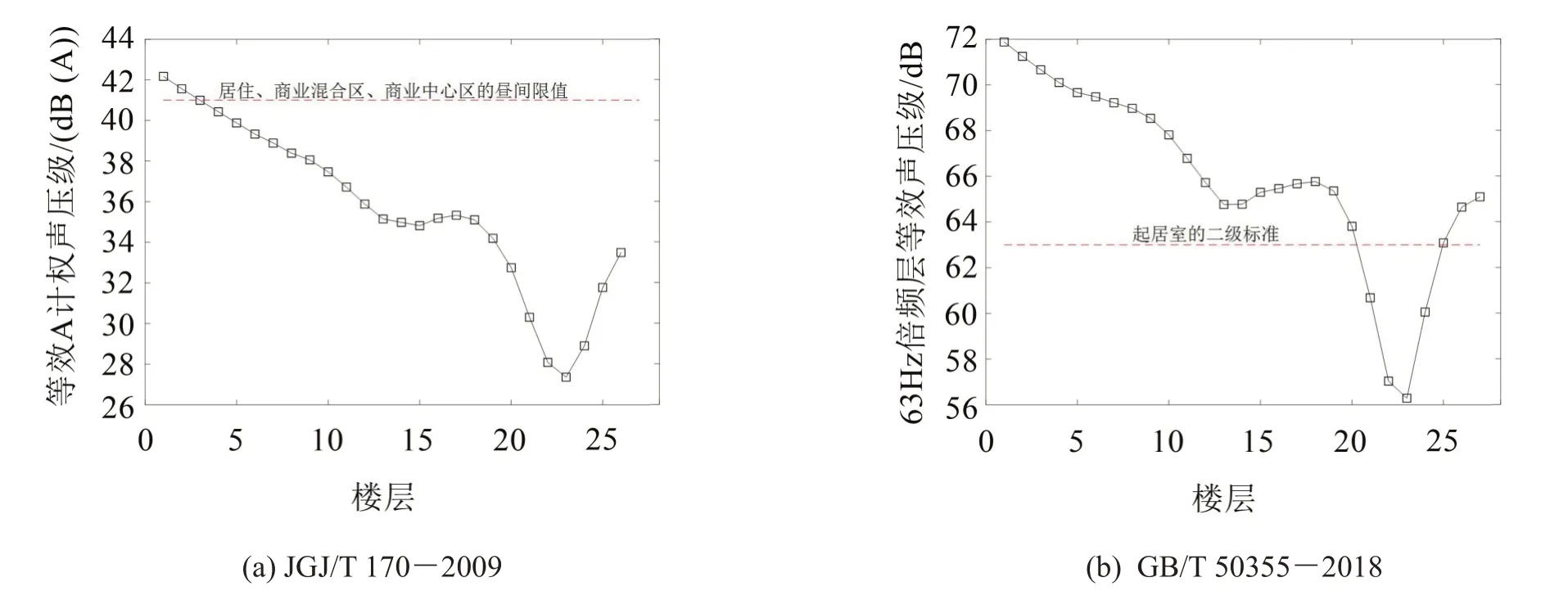
圖11 兩個結構噪聲評價標準得到的不同樓層聲壓級

3 結語

本文從地下綜合交通樞紐環保提升角度研究預測方法、評價標準及振動控制問題。以北京城市副中心站綜合交通樞紐為例，建立了上蓋建筑環境振動及二次結構噪聲預測模型，針對特定房屋結構進行環境振動及二次結構噪聲分析，得到如下結論：

（1）隨著樓層的增加，兩個標準（GB10070-1988和JGJ/T170-2009）給出的規律較為一致，即Z振級總體隨著樓層的增加而減小，但是在最后幾層會出現增大的現象；

（2）GB10070-1988 的計權值要小于JGJ/T170-2009 的計權值，在相同條件下，JGJ/T170-2009 的振動加速度級比GB10070-1988 大，根據JGJ/T170-2009計算結果更易超標。

（4）通過對比可知房屋結構環境振動超標風險較小，而二次結構噪聲超標風險較大，房屋結構的二次噪聲比環境振動更易超標。