借助幾何直觀構建筆算模型
——《兩位數乘兩位數的筆算（不進位）》教學設計與評析

執教|許桂霞 評析|倪芳華（特級教師）

【教學內容】

蘇教版三年級下冊第3～5 頁例3、“試一試”和“想想做做”第1～6 題。

【教學過程】

一、創設情境，復習引入

談話：為了讓同學們能吃到營養又可口的午餐，學校食堂的叔叔、阿姨們每天都精心挑選食材。你瞧，今天又給我們準備了新摘的迷你南瓜。

出示主題圖：請同學們仔細觀察，你從圖中知道了什么條件？又能提出什么問題呢？

【評析：新課伊始，教師創設了配置營養午餐情境，傳遞均衡飲食有助于身心健康的理念，激發學生學習探究的熱情。教師引導學生經歷收集信息、發現并提出問題的過程，不僅溫習了舊知，也為引出新知奠定了基礎。】

二、自主探究，明理通法

1.鏈接舊知，激活經驗。

列式：要算一共有多少個？該怎么列式呢？

估算:能估計一下24×12 結果大約是多少嗎？你是怎么估的？

生1：把24 看作20，把12 看作10，20×10 等于200，24×12 的結果大約是200 多。

生2：把12 看作10，24×10 等于240，24×12 大約是240 多。

談話：24×12 究竟等于多少呢？你想怎樣算？把你的想法圈一圈，把重要的步驟寫下來。

獨立完成《①號學習單》。

組織全班交流。

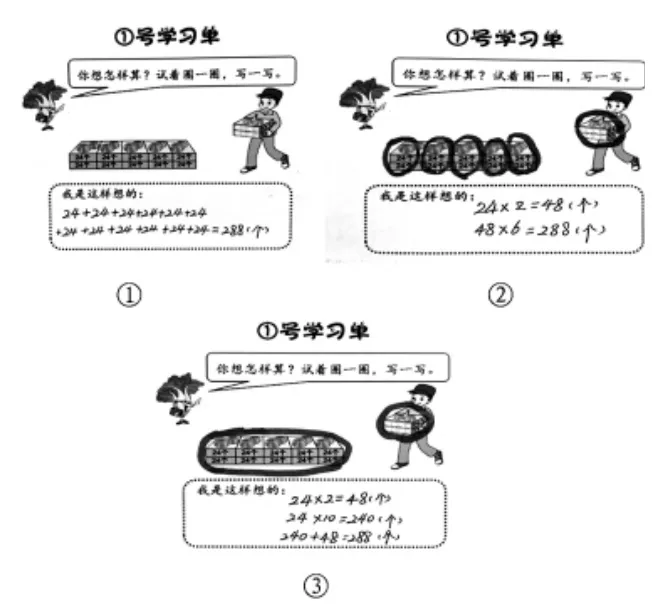
比較：比一比這幾種方法有什么相同的地方和不同的地方？

質疑：如果不是24×12，而是24×13，你選擇哪種方法呢？為什么？19×13 呢？

指出：看來“連乘”的方法，有的題能用，有的題不好用。但是，兩位數乘兩位數，都可以將其中一個兩位數拆成整十數和一位數，再分別和另一個兩位數相乘，最后把兩個和相加。

【評析：重視學生良好計算習慣的培養，讓學生先估再算，用估算來判斷計算結果的合理性，使學生體會到“估”的價值和魅力。在探究“24×12 究竟等于多少”這一環節，教師給予學生足夠的時空，學生結合主題圖呈現了自己的解法。方法一：轉化為連加算式；方法二：轉化為兩步連乘；方法三：轉化為求兩積之和。追問“24×13，19×13 你選擇哪種方法？為什么？”讓學生在多元算法中進一步優化，在比較辨析中感悟到，由“連加”變“連乘”的方法寫起來簡單，但又不具有普遍性。而唯有第三種算式模型背后具有豐富的意義，可以為理解筆算方法提供支持，并構建出筆算初步模型，同時，培養學生的開放性思維。】

2.探究算法，明晰算理。

自主探究：你們能根據以前的學習經驗，試著列豎式計算24×12 嗎？

獨立完成《②號學習單》。

提問：你們贊同幾號同學的寫法？為什么不贊同①號同學的計算過程？

指名學生介紹筆算方法：先算2 乘24，用個位上的2 依次乘24的每一位，得48；再算10 乘24，用十位上的1 依次乘24 的每一位，得240；最后算48 加240，得288。

提問：十位上的“1”乘第一個乘數個位上的4 得到的“4”表示多少，要和哪個數位對齊？

追問：結合例題圖指一指、說一說，這里的48 表示幾箱的個數？240 又表示幾箱的個數？288 呢？

指出：先算2×24，表示2 箱的個數，再算10×24 表示10 箱的個數，最后把兩部分合起來就是12箱的個數。

【評析：在學生嘗試列豎式計算后，教師引導學生回顧計算過程，在橫式與豎式的對比中理解每一步計算的意義，使學生感受和領悟到數量關系、分步橫式與豎式結構三者的聯系，從而找到知識的生長點和發展點。在經歷兩位數乘兩位數豎式計算的過程中，體會到口算和筆算雖然寫法不同，但其思路是一致的。豎式就是“站”起來的橫式，是將這里的三道橫式合在了一道豎式里，讓學生直觀形象地領悟了豎式原理，有效突破了教學難點，做到了算法與算理融合。】

3.數形結合，提煉算法。

拓展：24×12 這個算式還可以表示生活中很多其他的問題。例如：一箱礦泉水有24 瓶，有12箱，一共有多少瓶？再如：一排有24 個小朋友，有12 排，一共有多少個小朋友等等。

提問：看著點子圖，你能說說先算的是什么？再算的是什么嗎？筆算的每一步都能在點子圖上找到相應的部分嗎？

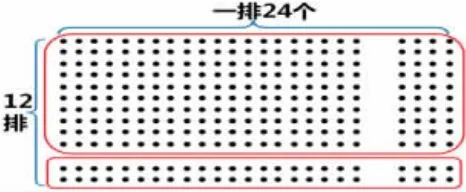
提煉算法：還記得我們剛剛研究的24×12 的豎式是怎么算的嗎？先算什么？再算什么？

根據學生敘述規范板書，并張貼對應的點子圖。

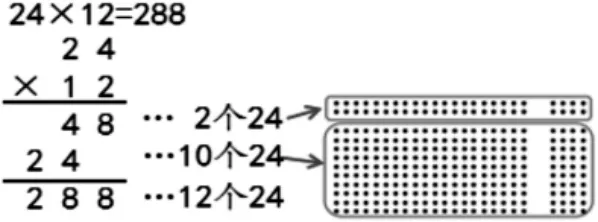
說明：為了書寫簡便，個位的0 可以省略不寫。想一想，如果把0 省略不寫，在計算第二步的時候需要注意什么？

糾錯：再幫①號同學看看，到底錯在哪里呢？應該怎樣改呢？

小結：兩位數乘兩位數，先用第二個乘數個位上的數乘第一個乘數，再用十位上的數乘第一個乘數；用哪一位上的數去乘，乘得的數的末位就和這一位對齊；然后把兩次的積相加。

談話：你能試著運用剛才的方法來算一算12×24 嗎？

比較：這兩道算式你發現了什么？乘法可以怎樣驗算呢？

小結：計算兩位數乘兩位數時，可以用調換乘數的位置再乘一遍的方法進行驗算。

【評析：巧妙地借助點子圖，將直觀的算理與抽象的算法緊密聯系在一起，學生學得輕松，理解得通透。“24×12 這個算式還可以表示生活中很多其他的問題”，學生對照課件呈現的點子圖自信地表達每步的意思，教師相機在黑板上張貼對應的點子圖，驅動學生在“變與不變”的思辨中，明晰乘法運算在不同情境中的應用，借助運算的意義建立形與式的關聯，同時感悟到豎式計算的簡潔美。由具體而形象的實例開始，最后賦予“24×12”一般的模型意義，滲透了初步的數學建模思想，促進學生思維靈活性的發展。在交換位置驗算時，教師利用可拆分的“配圖貼”進行操作，讓直觀表征有條有理，化靜為動，讓學生看得見、摸得著。在抽象與直觀、豎式與橫式、算理與算法的有效對接與溝通中，清楚感受到“法中見理，理中得法，原本不可剝離”，有效促進了學生“運算能力”核心素養的提升。】

三、鞏固練習，深化拓展

1.基本練習，鞏固內化。

（1）“想想做做”第1 小題。

交流算法：選擇一題和同桌交流一下，你是怎么算出來的？

比較：觀察我們做的五道題，有什么相同的地方？仔細觀察這幾題的計算過程，先想一想是分幾步來算的，再和同桌交流。

歸納算法：都是分三步來做，先用個位上的數依次去乘第一個乘數的每一位，再用十位上的數依次去乘第一個乘數的每一位，最后把兩部分的積加起來。

（2）“想想做做”第2 小題。

談話：你知道豎式中每一部分的積各是哪兩個數相乘得到的嗎？聯系題意說一說、填一填。

說明：這里的計算過程是先求1 個熱水瓶的價錢，再求20 個熱水瓶的價錢，然后相加得出21個熱水瓶的價錢。

2.變式練習，發展思維。

激趣：這里有個小朋友也做了兩道題，他做得對嗎？把不對的地方改正。

糾錯：指名學生說說錯在哪里？你覺得兩位數乘兩位數的筆算有什么要提醒大家注意的？

說明：在計算過程中，要注意積的數位，特別是用十位上的數去乘，乘得的數的末位要和十位對齊。在計算過程中，我們可以根據數據的特點，調換兩個乘數的位置，使我們的計算更簡便。

3.拓展練習，溝通遷移。

采用FLAC3D對隧道進行建模，按照施工開挖順序步對拱頂測點位移進行計算，并與預測位移進行比較，模型如圖6所示。

談話：研究兩位數乘兩位數的筆算是很有用的，可以幫助我們解決生活中的很多實際問題，你能幫李大爺算出一共有多少棵卷心菜嗎？

出示“想想做做”第6 題。

獨立完成，并全班交流。

遷移：如果把每壟32 棵改成每壟38 棵，38×13 該怎樣計算呢？如果改成321 呢？計算的過程中又會遇到什么新的問題呢？我們將在后面的課中繼續研究。

四、回顧梳理，總結提升

回顧：我們是怎么研究兩位數乘兩位數的筆算的？

小結：我們在觀察比較中明晰了算理，在合作交流中探索了算法，在數形結合中歸納了算法，最后在深化應用中提升了能力。

【課后總評】

本節課是在學生已經掌握了兩位數乘一位數和兩位數乘整十數的口算基礎上展開的。許老師設法引導學生將未知轉化為已知，感悟轉化的數學思想方法；借助模型溝通算理與算法，建立乘法豎式；運用多元表征，發展學生數學思維。整節課充滿著“生長”的氣息。

一、巧借轉化，促進知識“生長”

新課伊始，在探究24×12 到底得多少時，教師巧妙引導，搭建聯系新舊知識的橋梁，采用轉化的方法，在主題圖上分一分、圈一圈，借助數量關系進行算法理解，將新知轉化為已經學過的兩位數乘一位數的計算，與已有認知經驗進行了有效銜接，有效促進向新知的積極遷移。在計算——觀察——比較——辨析中，經歷計算方法“多樣化”到“普適性”的歸納過程，凸顯了計算道理的一致性與方法的多樣性。

二、數形結合，促進“理法”相融

理解算理、掌握算法是形成運算能力的兩翼。借助幾何直觀理解算理，形成算法，是學習運算內容的重要方法。許老師借助“點子圖”，幫助學生以“形”悟“理”。在圈一圈、畫一畫、擺一擺、算一算、說一說的學習活動中，巧妙地溝通了口算、筆算與圖形三者之間的關系。在“直觀”到“抽象”、“特殊”到“一般”的推理中，實現循理入法,以理馭法；在“怎樣算”“為什么這樣算”的追“根”溯“源”下，把握了計算教學的本質內涵。在分析的基礎上，建立乘法運算豎式，從算理過渡到算法，讓計算過程可視化，促使學生看得見算理，說得清思維過程，發展了學生的運算能力和推理意識。

三、搭建模型，尋找知識勾連

數學模型是數學知識的核心內容，它體現了數學應用的核心價值。在“怎樣書寫豎式可以清楚地記錄計算過程，并算出結果”的問題驅動下，教師留給學生足夠的時空，讓學生經歷解釋口算方法、創造筆算方法、對比橫式與豎式、歸納計算方法等學習過程，引領學生聚焦直觀模型、算式表征與計算方法之間的聯系，給學生思考、質疑、表達的機會，在多元對話中清晰地構建出兩位數乘法的豎式模型，體會豎式計算的優勢，使“算法”落地。在“鞏固練習，深化拓展”環節，教師充分挖掘教材資源，設計有層次的練習，進行多維訓練，提升運算能力，感悟筆算乘法解決實際問題的價值；借助模型思想進行拓展延伸，引導學生遷移類推：嘗試兩位數乘兩位數（進位）筆算乘法、三位數乘兩位數筆算乘法，溝通了乘法計算間的聯系，在整體中架構知識，引發學生向數學更深處漫溯。