讓學引思:讓數學課堂綻放異彩
——以“分數的意義”為例
劉必雄
江蘇省蘇州科技城實驗小學校 215004
新課改背景下,“讓學引思”教學理念應運而生。“讓學”指的是把學習的主動權讓位給學生,使學生成為課堂學習活動的主體。引思指的是教師要智慧“引思”,引導學生去思考,使學生更深入地學習知識[1]。蘇教版五年級下冊“分數的意義”是在三年級上冊“認識分數”的基礎上對分數的再認識和再探索,筆者以“讓學引思”教學理念為指導,對這節課的教學過程進行探索,力圖為在小學數學課堂中落實“讓學引思”教學理念提供某種借鑒或思考。
一、參與目標制定,激發學習內驅力
張奠宙指出:“教什么永遠比怎么教更重要。”“讓學引思”的教學模式下,“教什么”的問題是由教師和學生共同制定,極大地調動了學生學習的積極性和主動性,為學生提供了廣闊的舞臺。
師:同學們,在三年級我們已經學過了分數。誰能回憶一下,我們學習了分數的什么內容?
生1:我學會了讀分數和寫分數。
生2:我知道了分數由分母、分數線和分子三部分組成。
師:今天學習“分數的意義”。當你看到這個標題的時候,你還想了解關于分數的哪些知識呢?
生3:分數有什么用,為什么要學習分數?
生4:分數和整數之間有什么關系?
生5:分數與分數之間也能進行加減運算嗎?
師:看來同學們對“分數的意義”充滿了好奇。同學們提出的問題是我們這幾節課要為大家逐個解答的問題,我們這節課主要學習分數的產生、什么是單位“1”,什么是分數這些知識。現在,就讓我們走入“分數”的世界吧!
學生主動參與到學習目標的制定過程中,是其課堂主體地位的重要體現。在學生參與目標制定的前提下,教師要對學生提出的問題進行整理,并敏銳洞察這些知識目標隱含的教育價值,把學生的好奇心轉化成教學目標的設定,從而在課堂上去實現這些目標。
二、設境引思,初步感知概念
小學生的思維正在從形象思維向抽象思維過渡,教師有意識地為學生創設生動的、貼近學生生活經驗的教學情境,能夠為學生提供必要的感知素材,從而引發學生對教學內容的思考,激發學生學習的興趣[2]。
師:我手里有1 個蘋果,如果要把這1 個蘋果分給1 個同學,那么,1 個同學可以得到幾個蘋果?
生(齊):1 個。
師:對。如果我要把這1 個蘋果分給4 個同學,那么應該怎么分呢?
生3:這是我畫的圖(圖1)。我把1個圓平均分成4 份,取其中的1 份,這就是
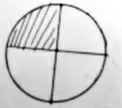
圖1
生4:我 把1 個正方形平均分成4 份,取其中的1 份,這就是(如圖2)。
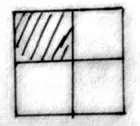
圖2
師:同學們畫得很好。那么,請同學們看看我畫的這個圖(圖3)能夠用來表示嗎?
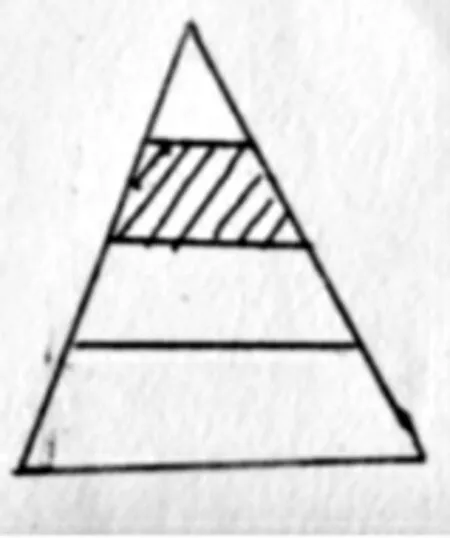
圖3
生(齊):不能。
生1:因為必須把三角形平均分成4 份,取其中的1 份,這樣才是
師:對。分數必須先要平均分,如果不是平均分,那就不能得到分數。
教學中,教師首先用“分蘋果”的情境為學生的學習創設了生動有趣的教學情境,激發了學生學習的主動性,使學生感受到分數來源于他們的現實生活,能為他們解決整數無法解決的實際問題;其次,教師引導學生自己畫圖表示,為了使學生更好地理解把1 個物體“平均分”的含義,教師智慧“引思”,通過反例使學生得出把1 個物體“平均分”是分數的前提條件。
三、抓住核心問題,學思結合探本質
“讓學引思”模式下,并非把所有的問題以簡單羅列的形式呈現在課堂上,而是抓住其中的“核心問題”引導學生在課堂上進行思考和探討,通過對“核心問題”的探討,使學生得出相關的概念和結論。“分數的意義”屬于典型的概念教學,數學概念的教學往往要從學生的現有經驗引入,通過具體例證引導學生分析、比較、概括、總結,從而得出概念的本質特征。
師:請同學們再看下面的圖(圖4),如果用1 個圓表示1,那么,4 個圓應該用幾來表示?

圖4
生(齊):4。
師:如果用2 個圓表示1,那么,4個圓應該用幾來表示(圖5)?

圖5
生:2。因為把2 個圓看作1,4 里面有兩個2,所以應該用2 表示。
師:如果用8 個圓表示1,那么4 個圓應該用幾來表示(圖6)?
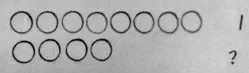
圖6
生1:因為“1”代表的數量不一樣。
師:同學們想一想,我們現在學習的這個“1”和我們一年級的時候學過的“1”表示的意義相同嗎?
生(齊):不一樣。
師:那么它們之間究竟有什么不同呢?誰能具體分析一下。
生1:這里的“1”代表的不是1 個,它只是一個參照對象,其他的物體都要跟它進行對比。
生2:我認為這里的“1”是一個標準,其他物體都要以它為標準進行比較。
生3:這里的“1”可以表示1 個圓,也可以表示很多圓。
師:同學們分析得非常好。看來同學們對“1”有了更加深入的認識。的確,這個“1”跟我們在一年級學的“1”并不一樣,我們課本上稱它為“單位1”。為了更好地認識“單位1”,讓我們來看下面的圖(圖7)。

圖7
師:如果用8 個圓代表“單位1”,那么,4 個圓應該怎么表示?
師:如果用2 個圓代表“單位1”,那么,4 個圓應該怎么表示?
生2:4 個圓表示為2。
師:同樣是4 個圓,為什么表示的各不相同呢?
生3:因為“單位1”不一樣。
師:那么,我們究竟應該怎樣認識“單位1”呢?
生4:“單位1”可以是1 個物體,比如1 個蘋果、1 張桌子等。
生5:“單位1”也可以是1 個圖形,比如1 個圓、1 個正方形、1 個三角形等。
生6:“單位1” 還可以是1 個計量單位,比如1 米長的繩子、10 米高的樹等。
師:對。1 個物體、1 個圖形、1 個計量單位都可以是“單位1”。那么,“單位1”可以是多個物體嗎?
生(齊):可以。
生7:“單位1”也可以是10 根香蕉。
生8:“單位1” 也可以是一個班的35 個學生。
生9:“單位1”也可以是10 棵樹木。
師:同學們分析得非常好。許多物體組成的一個整體也可以看作 “單位1”。也就是說“單位1”可以很大,也可以很小,“單位1”可以很多,也可以很少,我們可以把它們都看作“單位1”。
師:明白了“單位1”,誰現在能夠總結一下,什么是“分數”呢?
生1:把“單位1”分成幾份,表示取其中的1 份的數叫作分數。
生2:不對,應該是把“單位1”平均分成幾份,表示取其中的1 份的數叫作分數。
生3:不僅是取1 份,取多份也是可以的。
師:對。綜合同學們的觀點就是:把“單位1”平均分成若干份,表示這樣的1 份或者幾份的數叫作分數。
認識“單位1”是把握“分數的意義”中的“核心問題”,也是歷來教學上的難點。教學中,教師在學生自主思考基礎上,充分發揮“引思”的作用,先引導學生把1 個物體或者多個物體看作1,使學生意識到這里的“1”與一年級學習的數字“1”不是一個概念,進而引出“單位1”的概念。另外,針對“單位1”,教師讓學生充分發揮自己的想象力,列舉生活中的“單位1”,從而開闊了學生的視野,培養了學生的發散思維,使分數概念的形成水到渠成。
總之,“讓學引思”的教學理念集中體現了學生主體的思想,使學生最大限度地置身學習情境中,感悟知識產生的過程,從而達到激發學生探究欲望,優化學生思維品質的目的,這也是每一個教育者孜孜以求的終極目標。

