對一道教材例題的變式與引申*

合肥師范學院數學與統計學院 (230601) 李亞文 張新全

“變式教學”是我國數學教育的特色之一.由于“變式教學”的有效運用，使得我國學生在“雙基”方面的培養質量得到很大的提升.筆者研究了人教版和滬科版教材中的例、習題，對課本中的一道例題進行了變式教學的探討.

1.原題再現

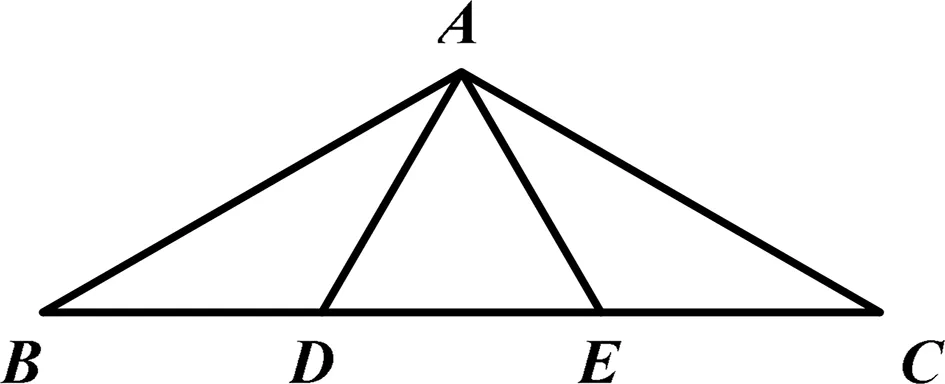
圖1

已知如圖1，在△ABC中，AB=AC,∠BAC=120°, 點D,E是底邊上兩點，且BD=AD,CE=AE.求∠DAE的度數.

在人教版和滬科版教材中，該題均是“等腰三角形”這一節的例題，文[1]和文[2]對這道例題做了深入的研究，在此不作贅述，本文將變換視角，對該題進行再變式.

2.變式探究

本題涉及等腰三角形的性質，三角形內角與外角的關系，沿著這樣的思路，可以得到下面的變式.

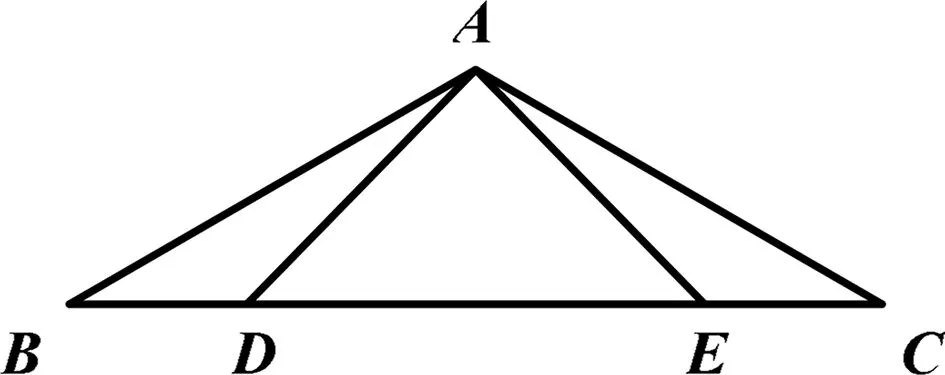
圖2

變式1 如圖2，點D,E在△ABC的邊BC上，AB=AC,AD=AE.求證：BD=CE.

這是人教版教材八年級上冊第82頁復習鞏固第6題，可以證明兩個三角形全等得到BD=CE,也可以作BC上的高，利用“三線合一”證明.

圖3

變式2 如圖3，P,Q是△ABC的邊BC上的兩點，并且BP=PQ=QC=AP=AQ，求∠BAC的度數.

這是人教版教材八年級上冊第83頁拓廣探索第14題，利用等腰三角形的性質可以求出相應角度的度數，是例題的逆向思考.

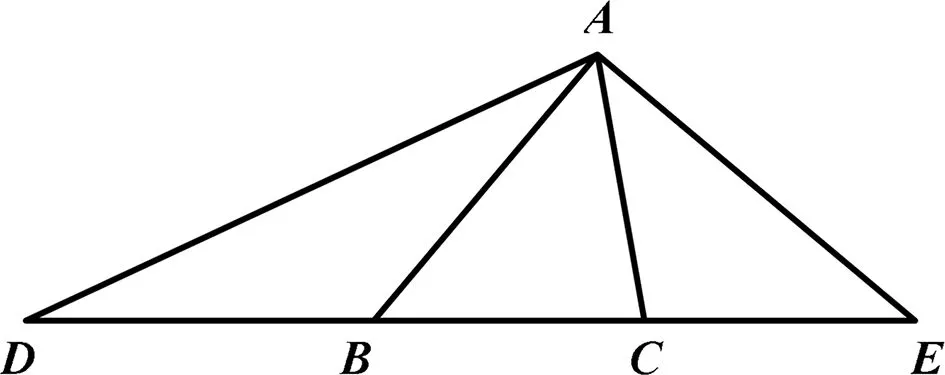
圖4

變式3 如圖4,在△ABC中，∠ABC=50°,∠ACB=80°,延長CB至D,使DB=BA,延長BC至E,使CE=CA,連接AD,AE.求∠D,∠E,∠DAE的度數.

這是人教版教材八年級下冊第91頁復習題13 復習鞏固第5題，是例題的簡單綜合.這里的三個變式，都是教材上的習題，起到鞏固基礎知識，訓練數學思維，提升思維能力的作用，所有這些問題仍然是比較簡單的，我們還可以繼續進行變式.

變式4 在Rt△ABC中，∠BAC=90°，點D、E在BC上，且BD=BA，CE=CA，求∠DAE的角度.

對例題中相等的線段改變位置，利用等腰三角形的性質，可以得到∠DAE=45°.

變式5 在ABC中，設∠BAC=α,點D、E在BC上，且BD=BA，CE=CA，求∠DAE的角度.

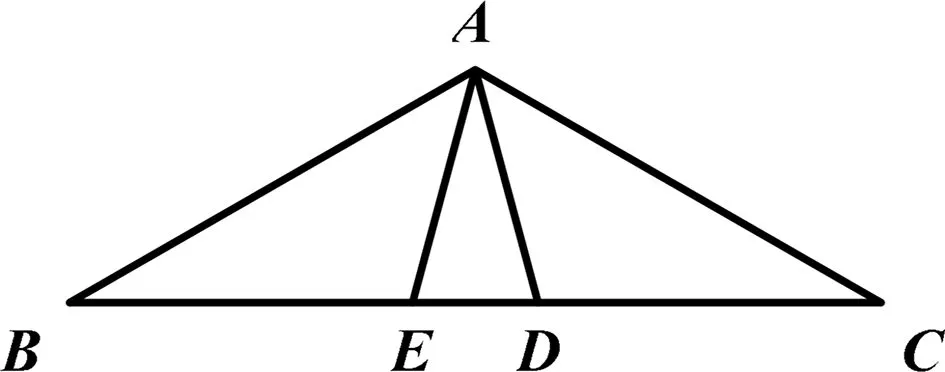
圖5

3.引申探究

引申1 如圖5，在△ABC,AB=AC=2,∠BAC=120°,點D,E是底邊上的兩點，且AB=BD,AC=CE,則線段AD的長等于( ).

解析：本題易構造出含30°角的直角三角形，此構造一旦達成就便于三角形中各線段長度的求解，又由全等三角形及相似三角形的性質和判定，利用方程思想，可以將求AD的長度轉化成一元二次方程的解.

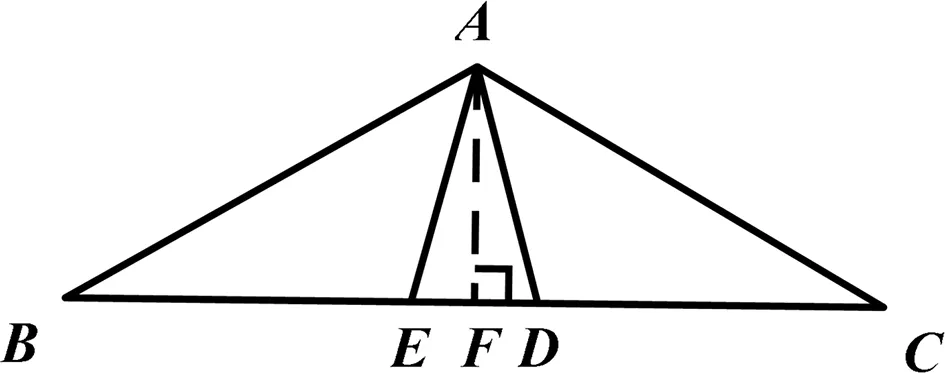
圖6

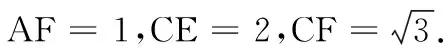
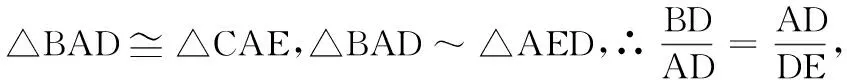
點評：此題解法靈活多變，讀者有興趣可以自行探究其他解法.本題解法涉及到分母有理化和開方，在中考中屬于較高要求，故不能作為中考題，但是可以作為課后探究題，讓學生課后探究.該題的呈現形式可以多變，既可以作為選擇題，又可以作為填空題和解答題，且該題的所求結果類型也可以為求角的大小和線段的長度.

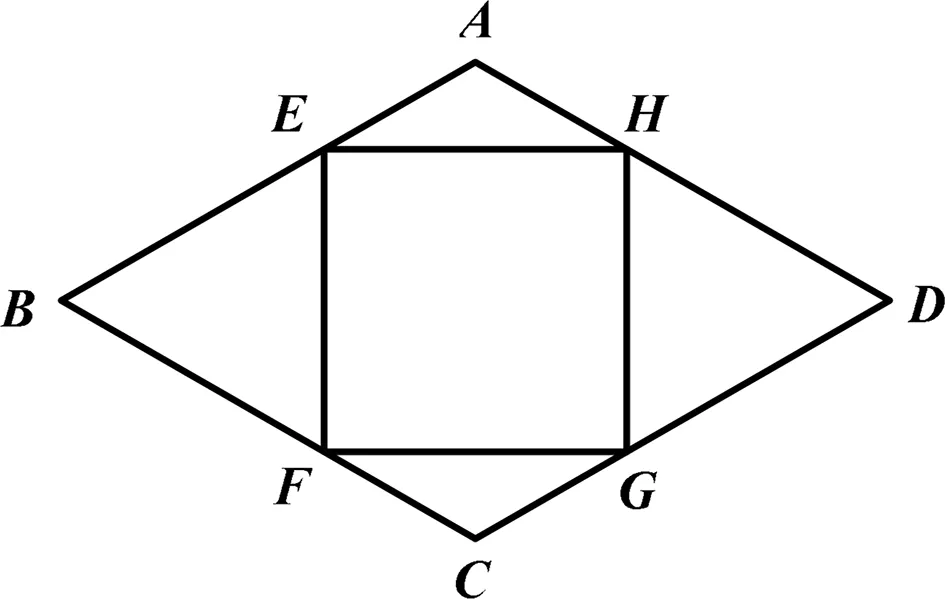
圖7

引申2 如圖7，在菱形ABCD中，AB=2,∠BAD=120°,點E,F,G,H分別在AB,BC,CD,DA上，則正方形EFGH的邊長為( ).

解析：學生利用幾何直觀，連接對角線，構造出含30°角的直角三角形，利用其性質設未知數，并用未知數表示各邊的長，再利用正方形的邊長相等，相等的量用不同的表示得到一元方式一次方程，求解即可得到結果.

圖8

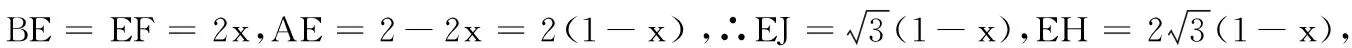
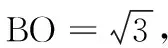
點評：該題根據對稱性將三角形構造成特殊的菱形，雖然初中生可以解出正確答案，但是解法還不夠嚴謹,比如(1)正方形EFGH是唯一存在的么?(2)正方形的邊EH、FG,EF、HG是否分別平行于菱形的對角線BD,AC呢?(3) 正方形EFGH的中心與菱形ABCD的中心重合么？因為初中學生是根據幾何直觀解題，并且已經默認了(1)(2)(3)成立，所以大大降低了該題的難度.

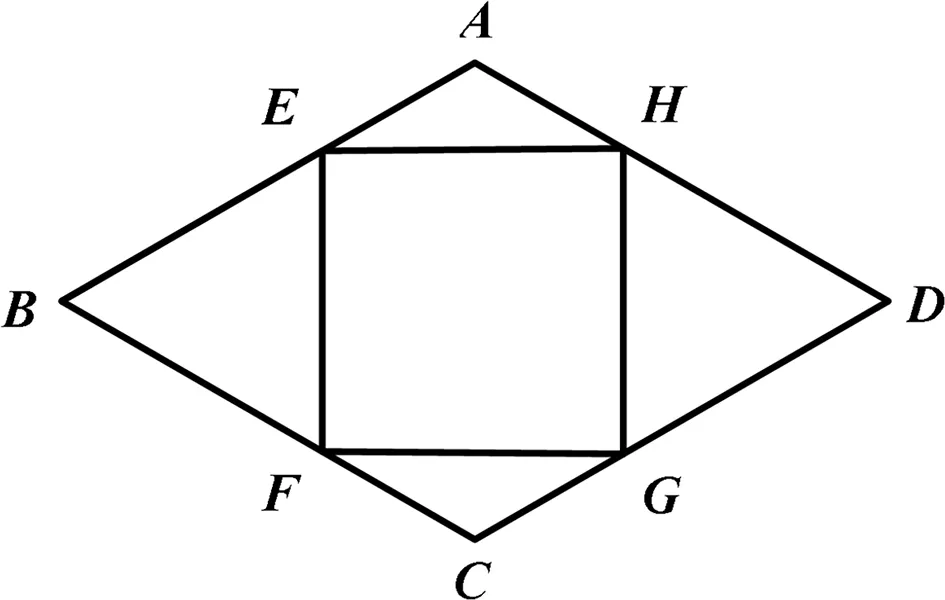
圖9

引申3 如圖9，在菱形ABCD中，AB=2,正方形EFGH的頂點分別在菱形ABCD的四條邊上.若△BEF是等邊三角形，則EFGH的長為( ).

解析：本題較引申2中，題目條件發生變化，但是難度降低了，具體方法見引申2，這里不再贅述.

點評：引申3是根據引申2中“正方形的邊EH、FG,EF、HG是否分別平行于菱形的對角線BD,AC呢”這一條件進行變式，由于四邊形ABCD為菱形，且△BEF是等邊三角形，這樣就直接避免了論證引申2中(1)和(2)、(3).感興趣的讀者還可以將△BEF是等邊三角形改變成△BEF是等腰三角形去求解.

以上的三個引申都涉及到分母有理化，對初中學生的數學素養有較高要求，但是考察的都是學生幾何解題的基本功——添加輔助線構造出含有30°角的特殊直角三角形，從而求出線段的長度.

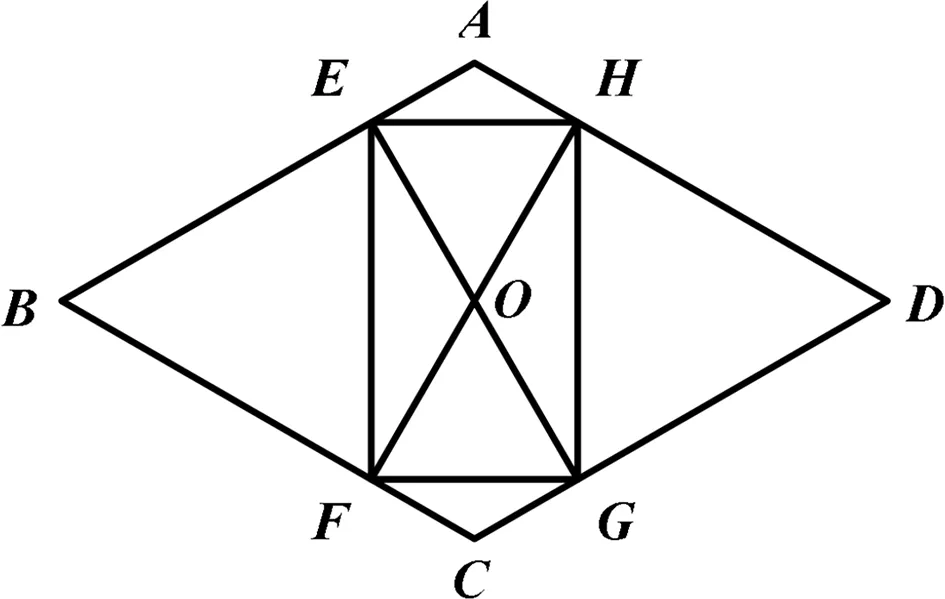
圖10

引申4 (2021年安徽省中考數學第8題)如圖10，在菱形ABCD中，AB=2，∠A=120°，過菱形ABCD的對稱中心O分別作邊AB,BC的垂線，交各邊于點E、F、G、H，則四邊形EFGH的周長為( ).

解析:菱形內接特殊矩形的周長計算，過程中考查模型的選擇與應用.能力要求等級B+C，依次求出OE=OF=OG=OH,利用勾股定理得出EF和OE的長，即可求出該四邊形的周長.

圖11

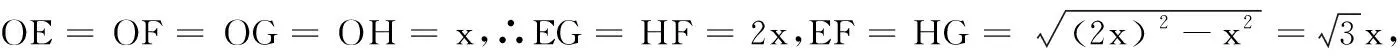
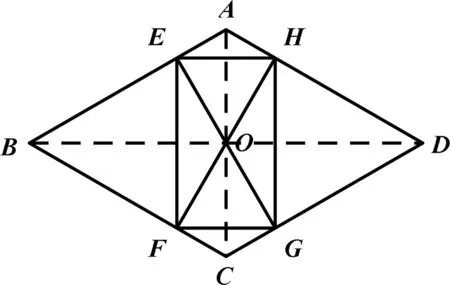
圖12

解法2：如圖12,連接AC、BD,交于O點，

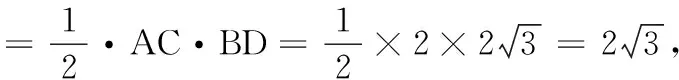
圖13

點評：本題圖形簡明，構造簡單，解題方向多樣，層次分明.求解時可以利用EH∥BD(或(EH∥AC))得到相似，構建等式方程求解，也可以連接OA,OB構造含30°的特殊直角三角形，先計算OE,再結合三角函數的定義求解各邊來實現；還可以直接運用面積法求解矩形對角線的長，再運用三角函數求解；也可以將EG(或FH)平移至與△ABC(△ACD或)的高重合來求解.題目比較基礎，但圖形內涵豐富，解法多樣，為不同的考生提供了不同的解題路徑，具有較高的效度和信度.

4.教學思考與總結

《教育大辭典》對“教學變式”的解釋為“在教學中使學生確切掌握概念的重要方式之一，即在教學中用不同形式的直觀材料或事例說明事物的本質屬性，或變換同類事物的非本質特征以突出事物的本質特征.目的在于使學生了解哪些是事物的本質特征，哪些是事物的非本質特征，從而對一事物形成科學概念.”數學變式教學的理論基礎主要有兩個來源，一是學習論基礎：建構主義學習理論強調通過積極自覺的認識活動來同化原有認知結構；奧蘇泊爾的有意義學習理論則強調學習者必須要理解符號所代表的新知識與原有的認知結構建立起非人為的實質性的聯系.這兩種學習理論的思想都是要求教學的變式來實現的，因此變式也是這兩種理論所提倡的.另一個教學理論基礎：隨機通達教學理論和腳手架教學理論也都對變式教學提出了要求，因為只有提供足夠的變式才能做到隨機通達，才能為學生搭起有效的腳手架.

大量的實踐證明變式教學是行之有效的，變式的對象有很多,如概念教學中的變式，定理、公式教學中的變式等.在課堂教學過程中，變式教學有助于讓學生更好地掌握數學知識方法的本質，有助于學生克服感性經驗帶來的消極影響，也有助于掌握一般方法,觸類旁通,舉一反三；變式教學有利于激發學生的學習興趣,有利于數學技能的掌握,有利于數學思想方法的掌握,有利于把握知識的本質,有利于形成良好的認知結構,有利于問題的解決.