一道2022年福建省高三聯考試題賞析

福建省福清三山中學 (350318) 念 杰福建省福清第三中學 (350315) 何文昌

數列的交匯試題常以壓軸題的形式出現．試題可以涉及函數、方程、不等式，三角函數與解三角形，解析幾何與立體幾何等知識，主要考查學生對數學知識的靈活應用、融合與遷移，考查學生數學視野的廣度、思維的深度和進一步學習數學的潛能．本文就一道福建省部分地市2022屆高三畢業班診斷性聯考12題為例，分析其求解與改編歷程，與同仁交流．

一、試題呈現

A．{S2n}是遞增數列 B．{S2n-1}是遞減數列

C．{bn-cn}存在最大項 D．{bn-cn}存在最小項

命題立意：本題主要考查數列的遞推公式、通項公式和前n項和、數列的單調性，三角形和圓等基礎知識；考查抽象概括與推理論證能力、運算求解能力；考查函數與方程思想、數形結合思想、分類討論思想、特殊與一般思想、有限與無限思想、化歸與轉化思想；考查數學抽象、直觀想象、邏輯推理、數學運算等核心素養；體現基礎性、綜合性與創新性．

二、解法探究

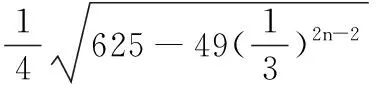
∴(b2n+2-c2n+2)-(b2n-c2n)>0，∴{b2n-c2n}是遞增數列，故{bn-cn}的最小項是b2-c2，D正確．同理，{b2n-1-c2n-1}是遞減數列，故{bn-cn}的最大項是b1-c1，C正確．故選A、C、D．

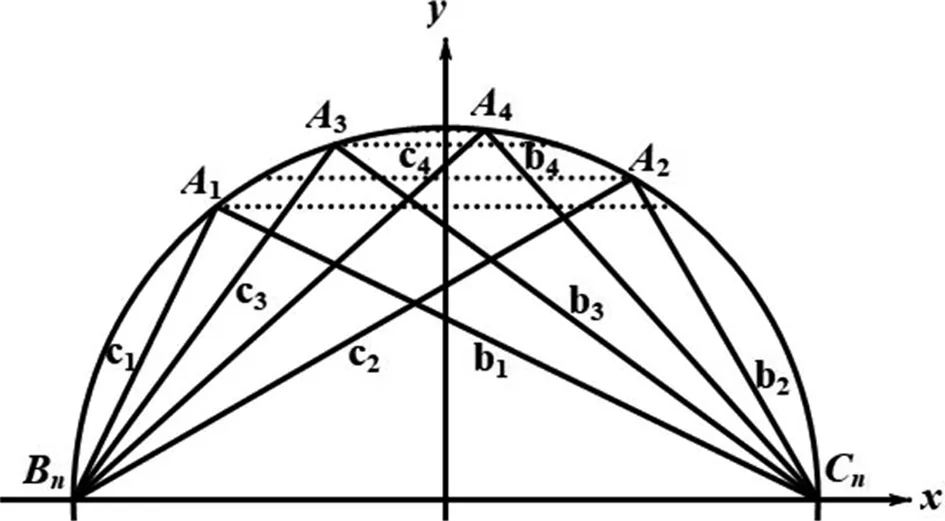
圖1

三、試題溯源

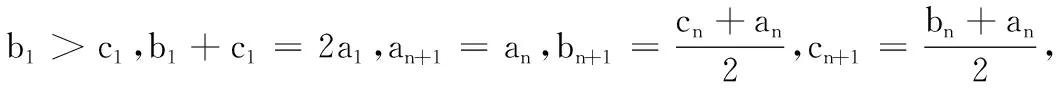
A．{Sn}為遞減數列 B．{Sn}為遞增數列

C．{S2n-1}為遞增數列，{S2n}為遞減數列

D．{S2n-1}為遞減數列，{S2n}為遞增數列

本題內涵豐富，新穎獨特，解題入口寬，路徑多，有較強的選拔功能，正是福建省2022屆高三畢業班診斷性聯考12題的源流．高考題的幾何背景是橢圓，福建省聯考題的背景是圓.

四、試題改編

把以上兩題的幾何背景換成雙曲線，得到改編題1．

題1 (多選題)設△AnBnCn的三邊長分別為an,bn,cn,周長為ln(n=1,2,3,…),內切圓半徑為rn,若a1=b1=4，c1=2，an+1=an，bn+1=cn+an，cn+1=bn+an，則( ).

A．{bn-cn}為常數列 B．{ln}為等差數列

C．{rn}存在最小項

D．{rn}既不可能為等差數列，也不可能為等比數列

把幾何背景換成拋物線，得到改編題2．

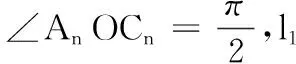
參考答案題1：B、C、D;題2：3；(n-1)2n+1+2.