例析阿波羅尼斯球的應用
2022-11-08 09:02:52江蘇省梅村高級中學214112陶煜瑾
中學數學研究(江西) 2022年11期
江蘇省梅村高級中學 (214112) 王 剛 陶煜瑾
平面上一動點到平面上兩定點的距離之比為定值(大于0),且定值不為1,此時,動點的軌跡為圓,稱之為阿波羅尼斯圓.類似的,空間一動點到空間內兩定點的距離之比為定值(大于0),且定值不為1,此時,動點的軌跡為球,稱之為阿波羅尼斯球,簡稱為阿氏球.下面舉例說明阿氏球的相關應用.

圖1
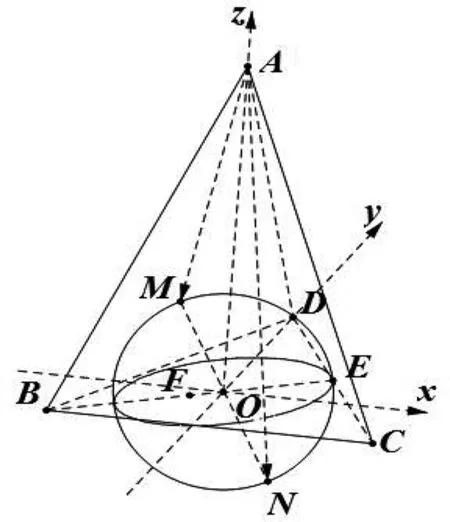
圖2
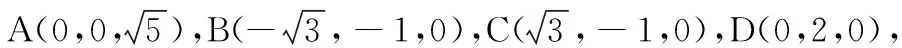
阿氏圓中涉及四個量,即平面內兩個定點,平面內動點軌跡方程,動點到兩定距離的比值,它們可以知三求一.當我們知道了一個定點,動點的軌跡方程,動點到兩定距離的比值可以求出第二個定點,我們發現這兩個定點連線通過圓心,并且它們到圓心的距離之積為阿氏圓的半徑的平方,我們把這兩個點稱作是這個阿氏圓的一對反演點.類似的,阿氏球中也涉及四個量,即空間兩個定點,空間動點軌跡方程,動點到兩定距離的比值,它們可以知三求一.當我們知道了一個定點,動點的軌跡方程,動點到兩定距離的比值可以求出第二個定點,我們發現這兩個定點連線通過球心,并且它們到球心的距離之積為阿氏球的半徑的平方,我們把這兩個點稱作是這個阿氏球的一對反演點.
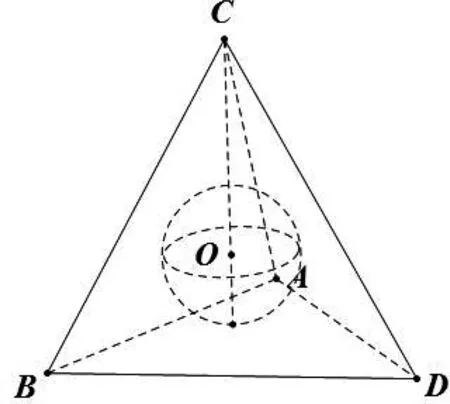
圖3

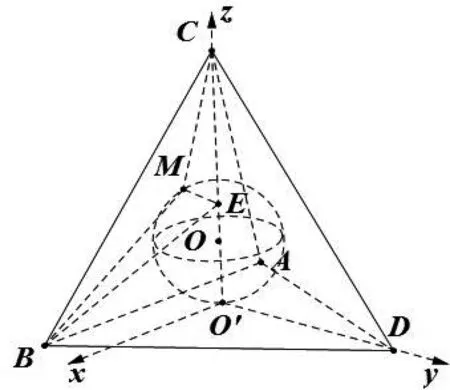
圖4

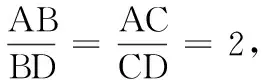
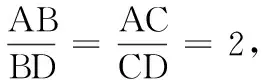

圖5

