數學課程內容下的數學建模教育

姜詠梅王志俊

（1.江蘇建筑職業技術學院公共基礎學院，江蘇 徐州 221116；2.中國礦業大學數學學院，江蘇 徐州 221116）

0 引言

眾所周知，數學建模是對現實問題進行數學抽象，用數學語言表達問題，進而用數學方法構建模型并解決問題的過程。數學建模是發展現代應用數學的重要突破口，它搭建了一個數學與外部世界緊密聯系的橋梁，是數學走向應用的必經之路。

對于大學生來說，各個領域的許多實際問題即使在了解了相關背景的情況下也很難借助于所學高等數學知識加以解決。究其原因，在高等數學教學過程中，教學內容理論推導和計算居多，應用性（特別是開放應用性）的教學內容偏少，數學教學內容和專業知識之間的銜接存在一定的問題。

對于此問題，葉其孝在將數學建模思想和方法融入高等數學課的教學方面做了深入的討論并提出了值得借鑒的建議。受此啟發，本文結合在國內具有一定影響力的五一數學建模競賽中一些典型題目，探討數學建模教育在數學課程內容方面的有機融合。

五一數學建模競賽是由中國礦業大學、江蘇省工業與應用數學學會和徐州市工業與應用數學學會聯合主辦的在國內具有一定影響力的數學建模賽事。該項賽事規模不斷擴大，2021年第十八屆五一數學建模競賽共吸引了近6 000支隊伍、17 000多名學生參賽；賽事質量也不斷提高，往屆賽題中許多問題的解決為相關單位帶來了良好的經濟和社會效益。五一數學建模競賽于每年的“五一”期間（連續72小時）以參賽隊為單位進行比賽，參賽隊從三道競賽題目中選擇一題進行解答并提交參賽作品。

1 課程內容及相關數學模型

在多數高等院校中，高等數學課程群主要包括高等數學、線性代數和概率論與數理統計三大課程。通過對這三大課程結構數學建模專題的內容要求和學業要求進行分析比對，結合五一數學建模競賽歷年來的賽題，選取了以下幾種常見的數學建模類型：基于指數函數的經濟數學和社會數學模型；基于線性方程組的線性規劃模型；基于統計學的聚類分析方法和線性回歸模型，以及相應的題目素材作為課程內容供參考使用。

1.1 基于指數函數的經濟數學和社會數學模型

指數函數是高等數學中所要研究的一類基本函數，是一種描述客觀世界變量之間指數增長或衰減關系和規律的數學工具，與指數函數相關的模型在許多領域有實際背景和具體應用。經濟數學模型和社會數學模型是數學建模專題所要研究的內容之一，而像存款貸款規模控制、經濟增長預測和人口增長預測等一些經濟社會實際問題均可通過指數函數模型來提供理論依據或解決方案。同時，在理解指數函數的概念以及其中所蘊含的運算規律的基礎上，學習基于指數函數的經濟數學和社會數學模型將有助于理解指數函數的實際意義，感受指數函數在刻畫增長率問題中的作用。

五一數學建模競賽2018年B題“商業銀行人民幣貸款規模分配及盈利問題”、2016年C題“二孩政策問題”、2015年C題“生態文明建設評價問題”和2014年“延遲退休問題”等分別由經濟和社會領域的實際問題加工而成。這些題目中的部分問題均可在簡單了解相關背景知識的基礎上，建立指數函數模型，進而尋得合理的解決方案。以2015年C題“生態文明建設評價問題”第四問為例，該題是基于某省生態文明建設改進措施效果的研究。對于如單位地區生產總值能耗、單位地區生產總值廢水排放量、綠化覆蓋率、人均公共圖書藏書量等指標，可以采用指數函數模型來研究其未來的變化趨勢。

1.2 基于線性方程組的線性規劃模型

作為線性代數的主要研究對象之一，線性方程組是一類簡單且重要的代數方程組。借助于矩陣和行列式，線性方程組的理論解法（如高斯消元法、克拉默法則等）已非常成熟；在計算數學中，其數值解法也日益完善。線性方程組有著廣泛的應用，科學技術中的許多問題均可歸結為解線性方程組。作為運籌學的一個重要分支，線性規劃研究線性約束條件下線性目標函數的極值問題。通俗來說，在實際問題（如生產安排、貨物運輸等）中，線性規劃是要找到一種最優的“方案”，使用或分配有限的資源（如原材料、車輛等）使得費用最省或者利潤最大，以達到預定的目標。

五一數學建模競賽2019年B題“木板最優切割方案”、2018年A題“徐州潘安湖風景區游覽路線設計”、2017年A題“公交車排班問題”和2013年C題“整車物流調動系統”等均以數學中的優化理論為基礎，根據題目要求建立目標函數，進而借助于計算機給出在特定約束條件下的最優解。而上述四道題目中對部分問題所建立的目標函數均是線性目標函數，均可以用線性規劃模型得到解決方案。

1.3 基于統計學的聚類分析方法和線性回歸模型

統計的教學活動應通過典型案例進行。應用統計是在概率與統計專題的基礎上展開的，而聚類分析和線性回歸模型是應用統計中的兩個主要內容。聚類分析是一種對數據集進行分析和處理，從中尋找相似元素，以達到分類目的的方法。對數據集進行分類的目的不同，聚類分析的方法也各異。在此過程中，筆者將結合具體實例介紹K-均值聚類和分層聚類這兩種易于接受的聚類方法。線性回歸是一種用來確定兩個或兩個以上變量間互相依賴的線性關系的一種統計分析方法。在許多領域，特別是在經濟學中，線性回歸常用來作為一種實證工具來預測各種指標。將介紹一元線性回歸和簡單的二元線性回歸模型以及利用最小二乘法原理對模型中的參數進行估計。

五一數學建模競賽2019年C題“科創板擬上市企業估值”、2018年B題“商業銀行人民幣貸款規模分配及盈利問題”和2008年“股指期貨套利問題”等題目都有來自不同領域的真實數據，都不同程度地涉及應用統計中的數據分析處理，進而確定不同要素之間的依賴關系或預測某一指標的走勢。以2019年C題《科創板擬上市企業估值》為例，通過對中國A股市場和美國NASDAQ市場相關數據進行聚類，然后利用多元線性回歸模型就可以定量分析估值水平與基本面指標、流動性指標之間的關系，進而給出差異性分析。這些方法和模型所得的相關結果對于研究我國科創板企業上市后的估值水平，都具有很好的參考價值。

2 數學模型應用與實踐

以2019年B題基于線性方程組的線性規劃模型“木板最優切割方案”為例。本題在切割大塊木板的過程中，需要設計合理的切割方案，從而降低生產成本，減少材料浪費，提高材料利用率，使家具廠經濟生產效益最大化。問題1～5均可歸結為線性規劃問題。比如在問題1中，為了使木板的利用率最大，只需產品P1的總面積最大，即一塊木板能切割產品P1的數量最多，可分別按長度和寬度進行優化組合，取兩者利用率更大者作為最終方案。以按木板長度優化組合為例，可以建立如下的數學模型：

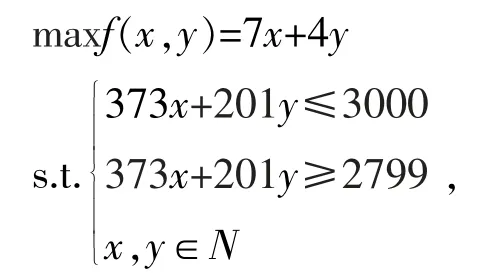
式中，x表示產品P1橫向排列的數目，y表示縱向排列的數目。顯然，該模型的目標函數f（x，y）為線性函數，約束條件為線性不等式，它是線性規劃模型。（注：x，y取自然數表明它還是一個整數規劃模型。）

注意到，當線性方程ax+ay=b變成線性不等式ax+ay≤b時，它在二維平面上就由一條直線變成該直線一側的半平面了。如上述模型中的線性不等式373x+201y≤3 000就表示直線373x+201y=3 000左側的半平面，373x+201y≥2 799就表示直線373x+201y=2799右側的半平面。因此，模型中的前兩個約束條件表示的是兩條平行直線中間的區域（如圖1所示）。

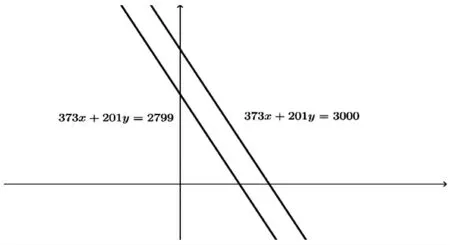
圖1

模型是要求和使得目標函數取得最大值，從直觀上看，越靠近直線的點取得的函數值越大。在不考慮是否為自然數的情況下，取得最大值的位于右側的直線上；當考慮和均為自然數時，取得最大值的應在中間區域且接近右側直線。而滿足這一條件的點只有。通過簡單的代入計算即得：目標函數取得最大值的整數解為且取得最大值59。該問題詳細討論了線性規劃模型與線性方程組之間的關系。

3 結語

結合數學課程內容開展數學建模教育的目的是希望學生能夠在學習數學知識的基礎上領略數學建模的思想和方法，提高學生學習數學的興趣和應用數學的意識和能力，進而體會到數學在現實生活中的應用。在這一過程中，恰當的數學建模素材和數學知識之間的有機融合往往能夠在教學上起到事半功倍的效果。從數學建模競賽賽題的建模方法中挖掘素材、凝練數學原理，進而在數學教學中有針對性地進行剖解分析；從數學建模競賽賽題的模型求解中發現方法、再現科學計算，進而在數學教學中有針對性地強化訓練。這樣就達到了將數學建模思想滲透到整個數學學習中的目的，從而提高學生的綜合素質，為學生的可持續發展奠定基礎。