溫故知新,提升復習課的效率
——以“銳角三角函數的復習課”為例
范 雷
山東省淄博市張店區第十二中學 255000
馮 姣
山東省淄博市張店區人民東路小學 255000
數學復習課既要做到回頭望,對已經學習的知識進行鞏固復習,又要在復習過程中產生新的認識,構建新的知識體系,產生新的理解.在數學復習課中,要防止學生對學過的知識感到厭倦,在課堂上沒有積極性,就需要教師進行精巧的設計,用新穎的題型和情境吸引學生的注意力.在復習過程中還要注意通過歸納和總結,幫助學生構建知識體系,理解解題的思路和方法,提升解題能力.下面筆者以復習銳角三角函數為例,談一談復習課的教學策略及如何提高復習效率.
有效提問,有效指導
復習課教學都是知識再現,因此教師設問顯得尤為重要,“好的問題”能激發學生的學習興趣,能帶給學生深刻的感悟,能促使學生不斷成長.故教師設問不能隨意,必須有的放矢,有重點、有目標,能最大限度地激發學生的好奇心和求知欲,使課堂教學的開展更加流暢自然.
案例1如圖1所示,在Rt△ABC中,∠ACB是直角,AB⊥CD,已知BD=2,求AC的長度.
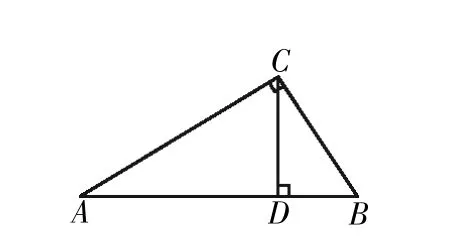
圖1
師:要解決這個問題,可以通過解哪些直角三角形完成?
師:這是由特殊的三角函數得到的.
生2:在Rt△BCD中,根據勾股定理可 得BC=4.在Rt △ABC 中,AC=BC·
師:很好,這是由勾股定理得到的.
生3:在Rt△ABC中,∠ACB為直角,CD垂直于AB,所以∠ADC和∠CDB相等,∠ACD和∠B相等,所以△ADC和△CDB相似,所以,所以AC=
師:很好,生3是通過相似三角形的性質得到的.
生4:老師,我也是通過勾股定理得到的,但是具體步驟與生2不同.在Rt△BCD中,根據勾股定理可得BC=4.設AC=x,則AD=,由面積法可得,解得A
師:非常精彩.由同學們給出的幾種方法,我們可以看到三角函數多個角度的運用.
在進行定義和概念的復習時,教師應該盡量避免問題的碎片化和零散化,如復習三角函數時直接提問:“說出銳角三角函數的定義及特殊角的三角函數的定義.”這樣的問題缺少思考性,難以調動學生的興趣,也不利于營造良好的課堂氛圍.本例中,通過將三角函數知識蘊含于題目中,使學生從多個角度觀察問題,培養了思維的靈活性,真正理解了三角函數的定義,在輕松的氛圍中提升了學習效果.
有效閱讀,透析本質
復習課教學中需要從學生已有的知識和生活經驗出發創設情境,讓學生在體驗情境的過程中理解數量關系和變化的規律,使學生能在體驗情境的過程中建立數學模型,將知識運用到實際問題的解決中去,加強方程、不等式以及三角函數等知識之間的聯系.
案例2如圖2所示,在廣場上空有一個氣球A,地面上三點B,C,D在同一條直線上,BC長20 m,在點B,C處分別測得氣球A的仰角∠ABD為45°,∠ACD為56°,求氣球A距離地面的高度AD(精確到0.1 m,tan56°≈1.483).
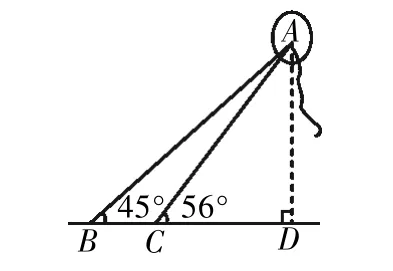
圖2
師:怎樣用好三角函數知識解決這個問題呢?同學們思考一下:氣球A距離地面的高度AD可以利用哪個直角三角形求解?
生5:可以利用Rt△ABD或Rt△ACD求解.
師:圖中的這兩個直角三角形除了已知∠ABD=45°,∠ACD=56°外,缺少什么條件?它們之間有什么內在的聯系?
生6:這兩個直角三角形都缺少已知邊的條件,但是它們有一條公共的直角邊AD,我們可以設CD為x m,用x的代數式表示BD,再通過公共邊AD得到變量之間的相等關系.即(20+x)tan45°=xtan56°,解得x=,所以AD=tan56°≈61.4(m).
師:根據生6的思路,我們需要找到固定不變的量,也就是氣球的高度,再通過三角函數求高.

師:這兩種方法分別從直接和間接兩個角度求解,我們的生活中也有這樣的問題嗎?接下來讓我們看看下面兩道題,能否進行類比和轉化呢?
題1:如圖3所示,一條小河的旁邊有一座山,從山頂的A 點俯瞰小河的C點和D點,分別得到夾角的度數為30°和45°,這條小河的寬度CD為50米.若現在從山頂的A點拉一條筆直的纜繩AC到小河對岸的C點,你能求出纜繩AC的長嗎?
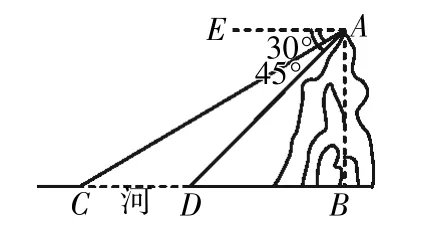
圖3
生8:作CD 的垂線AB,且AB 與CD 的延長線相交于點B.根據俯角的定義,可知AE 與CD 平行,得到∠C 和∠ADB 的度數分別為30°和45°,從而得到類似于案例2 的問題.
題2:某礦物探測隊探測到一幢廢墟建筑的下方點C處有礦物質,觀察圖4可知,在地面上探測隊挖掘了兩個探測點A和B,它們之間的距離為3米,A點處的探測線與地面形成的夾角為30°,B點處的探測線與地面形成的夾角為60°,試確定點C的深度.(參考數據:
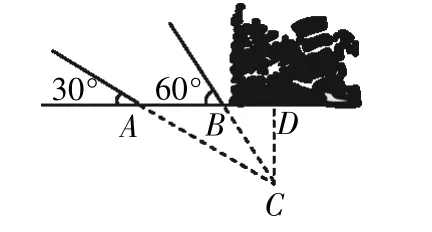
圖4
生9:如圖4 所示,本題同樣通過作輔助線進行解決,即過點C 作CD 垂直于AB,與AB 的延長線相交于點D,然后通過所學的相關定理轉化為上一類問題.
在掌握所學知識的基礎上,再次尋找新的問題,經過反思和總結可以鞏固已學知識,并促進知識深化以及思維進一步發展.經過習題的拓展和延伸,引導學生透過現象抓住問題的本質,發現知識之間的內在聯系,在解題和反思中鞏固知識,深化理解,學會解直角三角形的方法,提升學生的適應能力,掌握解題技巧.
有效探究,深入反思
復習課教學中,教師應基于學生的認知規律進行教學設計,有效激發學生學習的主動性,給學生充分參與數學活動的機會,引導學生積極主動地探索和交流,掌握數學的基本技能,體會數學思想,學會數學方法,積累數學活動經驗.
案例3根據市里對建筑的要求,建筑樓房需要保證采光時間,因此樓房之間的距離不能太小,至少要保證中午12時是有陽光照射的.
如圖5所示,現在需要在一幢舊樓的正南方建一幢新樓,兩樓的距離為40 m,舊樓的一樓窗臺高1 m,根據統計該地冬天中午12時太陽從正南方照射的光線與水平線的最小夾角為30°,為了提高收益,需要計算新樓最高可建多少米.
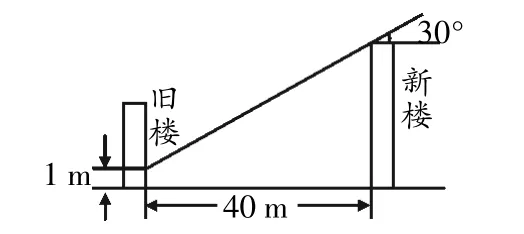
圖5
生10:在符合規定的情況下,我們可以利用三角函數求解,圖5中新樓與舊樓之間可以建構直角三角形,保證陽光照射到一樓窗臺.

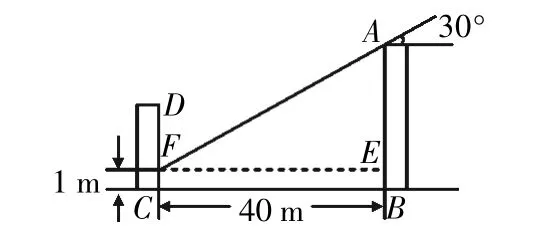
圖6

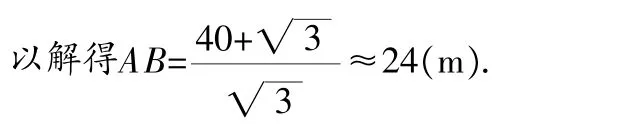
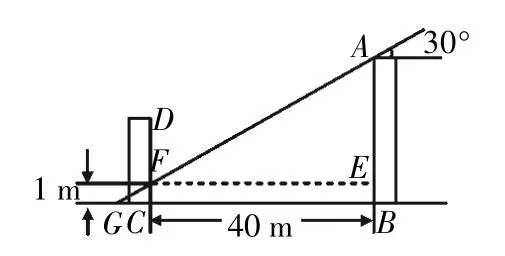
圖7
教學要挖掘知識的本質和內涵,案例3在傳授知識的同時,通過試題訓練,并采用一題多解的方法,鍛煉學生思維的靈活性,讓其掌握多種解題方法,深入體會數學思想和本質.
變式練習,彌補缺陷
銳角三角函數的知識需要在直角三角形的基礎上應用,但是在解決問題的過程中,經常發現很多問題的難點就在于沒有現成的直角三角形可以利用,必須進行構造.因此在銳角三角函數的教學中,構造直角三角形與銳角三角函數進行聯系是一個重要的教學內容,需要通過變式練習加強引導和思考,提升學生的思維深度.
案例4如圖8所示,△ABC的頂點是正方形網格的格點,則sinA 的值是多少?
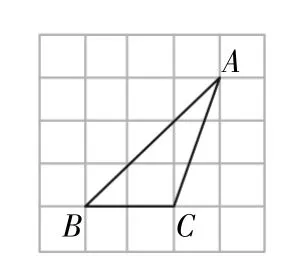
圖8
師:這道題同樣需要用到三角函數,我們怎樣才能找到這個“三角函數”,如何使用它?想要解決這個問題,先要將∠A 放到直角三角形中,但觀察圖形△ABC并不是直角三角形,因此必須通過添加輔助線來構造直角三角形,那么如何構造這個直角三角形呢?

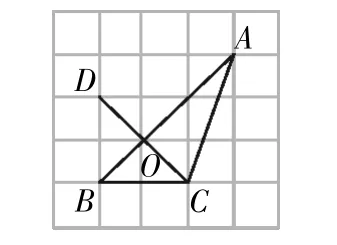
圖9
變式1:六個小正方形組成一個網格(如圖10所示),小正方形的邊長相同,小正方形有頂點A,B,C,D,AB和CD相交于點P,則tan∠APD的值是多少?
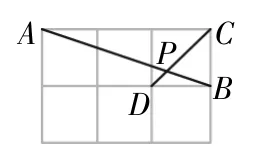
圖10
生12:如圖11所示,通過對頂角相等、正方形的對角線性質可得∠APD=∠BPF,△PBF為直角三角形.由△DPB∽△CPA得,從而PF=在Rt△PBF中,可得tan∠BPF=
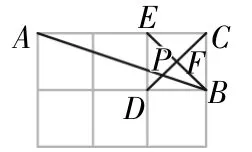
圖11
生13:我還有其他方法,如圖12所示,先連接AE和BE,可得Rt △AEB;由平行線的性質、正方形的對角線性質和同位角定理可得:在Rt△AEB中,tan∠APD=tan∠ABE=
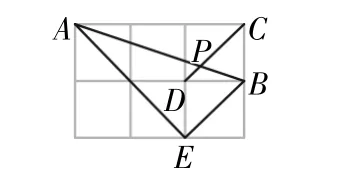
圖12
通過變式訓練,應用一題多變、一題多解等多種習題講評的有效方式,使得學生可以從多個角度調動知識,實現知識的系統化、網格化,有利于建構知識體系,提高學習效率,實現主動學習.
綜上所述,數學學習是一個思維不斷完善的過程,本課通過勾股定理、特殊角的三角函數和相似三角形等知識解決問題,引導學生認識到生活中三角函數應用的廣泛性.在例題設計的過程中,教師通過有效的提問,抓住數學的本質和變式訓練等對學生所學知識加以鞏固,全方位地調動學生學習的積極性,能提高學生思維的能動性,讓學生在輕松愉快的氛圍中提升學習效率.

