股票市場中不完全信息兩階段博弈分析

許 璐，葉 咪

(南京財經(jīng)大學(xué)，江蘇 南京 210023)

一、 引言

(一)股票市場現(xiàn)狀

股票市場上主要有“莊家”和“散戶”兩種投資者，“莊家”即機構(gòu)投資者，“散戶”即個人投資者。機構(gòu)投資者在獲取信息上有自己獨有的途徑；而個人投資者只能根據(jù)市面上龐大而雜亂的信息，辨別信息的真?zhèn)危M(jìn)行股票投資選擇。 機構(gòu)投資者在信息上占據(jù)優(yōu)勢地位，可以利用途徑獲取和散布信息。因此，在機構(gòu)投資者與個人投資者之間存在博弈。

不僅機構(gòu)投資者與個人投資者之間存在博弈，機構(gòu)投資者之間同樣存在博弈。 大型機構(gòu)投資者的資金與信息掌握程度和小型機構(gòu)投資者資金與信息掌握程度不同，操縱股票價格的能力也不同。 股票投資者是在追求一定利益的情況下，才會愿意承擔(dān)股市的風(fēng)險，因此投資者的最終目的一定是獲得盡可能大的收益。 大型機構(gòu)投資的資金充足的同時野心也大，對利益的追求較小型機構(gòu)投資者來說更大，小型機構(gòu)投資者不可避免地成為大型機構(gòu)投資者的博弈對象。 縱觀A 股市場投資狀況，也可以得知相較于散戶的博弈而言，機構(gòu)投資者之間的博弈更為激烈。 因此，可以通過研究機構(gòu)投資者之間的博弈情況，分析在目前市場的狀況下對博弈雙方而言的均衡解，進(jìn)一步分析是否存在改進(jìn)空間，并分析這種解出現(xiàn)的實際意義。

(二)研究現(xiàn)狀

股票市場的有效性假說表明，市場知道所有已知信息，市場的參與者是平等且信息對稱的。 在20世紀(jì)60 年代有效市場假說獲得了廣泛的學(xué)術(shù)信任。但肖欣榮和田存志[1]利用博弈分析框架，基于中國證券市場投資主體的結(jié)構(gòu)，在負(fù)指數(shù)效用函數(shù)假設(shè)下，對大戶的分離定價策略和混同定價策略進(jìn)行了研究，進(jìn)而證明了股票市場的無效性。 并且結(jié)論表明，大戶的定價策略與其風(fēng)險厭惡系數(shù)有關(guān)。

對股票市場的博弈研究主要是基于博弈參與者為個人投資者和機構(gòu)投資者的博弈分析。 基于股票市場獨特的特點，對個人投資者和機構(gòu)投資者的博弈行為的研究，都是在同一個前提下進(jìn)行的——博弈雙方信息不對等，即不完全信息下進(jìn)行靜態(tài)或者動態(tài)博弈。

賀小剛[2]發(fā)現(xiàn)在證券市場上，個體投資者是信息與資金的弱勢群體，上市公司可能會在市場上傳遞利己的信息，給個體投資者的投資決策造成極大的信息不對稱。 趙月[3]認(rèn)為在不完全信息動態(tài)博弈下，個人投資者產(chǎn)生跟風(fēng)行為的可能性隨著個人投資者產(chǎn)生跟風(fēng)行為與不產(chǎn)生跟風(fēng)行為的收益之差的變化而產(chǎn)生改變。 陶欣和譚克[4]通過建立一個二級市場中“莊家”與中小投資者的不完全信息動態(tài)博弈模型，試圖說明在一個階段中中小投資者根據(jù)期望效用最大化進(jìn)行的決策。

(三)研究方法和內(nèi)容

通過研究機構(gòu)投資者之間的博弈情況，建立相應(yīng)的博弈模型，進(jìn)行兩階段的分析。 通過機構(gòu)投資者之間的支付矩陣，分析均衡存在的可能以及其現(xiàn)實意義。 研究認(rèn)為，在非合作博弈下只要機構(gòu)投資者之間在沒有溝通的情況下有默契達(dá)成一致決策，即可以從散戶手里得到相當(dāng)?shù)氖找妫颂幍臋C構(gòu)投資者之間的博弈我們不考慮散戶的收益狀況。 當(dāng)雙方機構(gòu)投資者沒有足夠的默契達(dá)成一致的決策時，散戶可以從中得到一部分的收益，因此機構(gòu)投資者中必有一方要承擔(dān)相應(yīng)的“損失”，這種損失不是本金的損失，只是相比于在該博弈過程中獲得收益多的一方比另一方多得到的收益部分，我們認(rèn)為這是某種程度上的損失。

二、 模型假設(shè)與分析

股票市場的參與者主要是機構(gòu)投資者與散戶兩類的投資者，機構(gòu)投資者與散戶投資者之間存在博弈競爭，同時機構(gòu)投資者之間也存在博弈競爭。 股票市場的博弈實際上就是零和博弈。 總的股票池是一定的，有人盈利必定有人要承擔(dān)相應(yīng)的損失。

李卓石和劉慶懷[5]分析了個人投資者與機構(gòu)投資者之間的博弈模型，同時也分析了機構(gòu)投資者之間的博弈競爭。 本文所建立機構(gòu)投資者之間的博弈模型與其所提出的模型存在不同。 李卓石和劉慶懷所做的模型為一次性靜態(tài)博弈，而本文將在其假設(shè)的基礎(chǔ)上建立新的假設(shè)，建立兩階段的動態(tài)博弈模型。

假設(shè)1:兩個機構(gòu)投資者同時擁有某只股票的部分份額，其余部分為散戶所持有。 由于單一散戶的資金實例不如機構(gòu)投資者，對股票市場的股價幾乎不會產(chǎn)生影響。 機構(gòu)投資者1 與機構(gòu)投資者2 為理性人。 機構(gòu)投資者1 與機構(gòu)投資者2 均以同一價格P申購份額或者贖回份額所對應(yīng)的資金。 機構(gòu)投資者1 申購或贖回的份額為q1，機構(gòu)投資者2 申購或贖回的份額為q2。 兩個機構(gòu)投資者在不進(jìn)行溝通情況下獨自選擇買入還是賣出，以使其利潤最大化。

假設(shè)2:機構(gòu)投資者1 與機構(gòu)投資者2 同時買入或賣出，則可以控制股票價格，即在最高點賣出，在最低點買入。 若機構(gòu)投資者1 與機構(gòu)投資者2 買賣操作不一致，則持股份額多的一方可以操縱股市。

根據(jù)股市交易的特點，交易操作時間很短，可以忽視交易期間股價的波動。 設(shè)買入或者賣出股票時每份額股票的價格均為p，交易后股價上漲則每份額的股票價格為p＋1，交易后股價下跌則每份額股票的價格為p-1。 在此期間，我們也不考慮其他的股票折算方法，默認(rèn)用現(xiàn)金進(jìn)行股票交易。 進(jìn)行股票買賣時，會產(chǎn)生一定的手續(xù)費，本文模型中設(shè)交易過程中產(chǎn)生的手續(xù)費為0，即不考慮交易過程中產(chǎn)生的手續(xù)費。

第一階段:雙方機構(gòu)投資者對對方的投資行為不了解，只能根據(jù)自己得到的內(nèi)部信息和外部信息進(jìn)行買賣交易。 若賣出后，股價上漲則認(rèn)為該策略虧損相應(yīng)的金額。

情形一:機構(gòu)投資者1 與機構(gòu)投資者2 都選擇買入，則二者可以操縱股市，使得股票價格上漲，從而使得該策略獲得一定的利益。

機構(gòu)投資者 1 的利潤為:π1＝(p＋1-p)q1

機構(gòu)投資者 2 的利潤為:π2＝(p＋1-p)q2

情形二:機構(gòu)投資者1 與機構(gòu)投資者2 都選擇拋出份額，同樣地，二者可以操縱股價，使得賣出的價格為最高價，即使得后續(xù)的股票價格下跌，從而獲得相對較高的收益。

機構(gòu)投資者1 的利潤為:π1＝(p-p-1)q1

機構(gòu)投資者2 的利潤為:π2＝(p-p-1)q2

情形三:機構(gòu)投資者1 選擇買入，機構(gòu)投資者2選擇拋出份額，則進(jìn)行股份交易多的一方可以操控股價，從而使得資金雄厚的一方在與其他方進(jìn)行博弈時，處于優(yōu)勢地位；而交易份額相比之下較少的一方，成為股市博弈的犧牲者。

機構(gòu)投資者1 的利潤為:

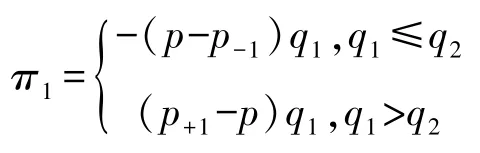
機構(gòu)投資者2 的利潤為:

情形四:機構(gòu)投資者1 選擇拋出份額，機構(gòu)投資者2 選擇買入，同樣地，進(jìn)行股份交易多的一方可以操控股價，從而使得資金雄厚的一方在與其他方進(jìn)行博弈時，處于優(yōu)勢地位；而交易份額相比之下較少的一方，成為股市博弈的犧牲者。

機構(gòu)投資者1 的利潤為:

機構(gòu)投資者2 的利潤為:

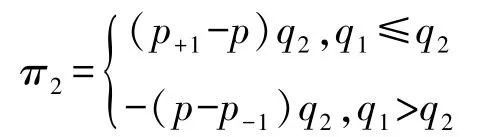
由上述四種情形可以得到機構(gòu)投資者1 與機構(gòu)投資者2 之間博弈的支付矩陣。 (表1)

表1 機構(gòu)投資者與機構(gòu)投資者2 第一階段支付矩陣

對該支付矩陣進(jìn)行分析:

(1)當(dāng)q1＜q2時

若機構(gòu)投資者1 選擇買入，則需要比較機構(gòu)投資者 2 買入和賣出策略收益的大小，即比較(p＋1-p)q2與(p-p-1)q2的數(shù)量關(guān)系；若機構(gòu)投資者1選擇賣出，機構(gòu)投資者2 的策略選擇與前面情況一樣。

比較(p＋1-p)q2與(p-p-1)q2，即比較p＋1-p與pp-1，也就是比較股票上漲價格和交易價格之差與股票下跌價格和交易價格之差的數(shù)量關(guān)系。 當(dāng)股價上漲幅度大于下跌幅度時，機構(gòu)投資者2 選擇買入；當(dāng)股價上漲幅度小于下跌幅度時，機構(gòu)投資者2 選擇賣出相應(yīng)的份額。

若機構(gòu)投資者2 選擇買入，則機構(gòu)投資者1 選擇買入對其來說是最好的策略；若機構(gòu)投資者2 選擇賣出，則機構(gòu)投資者1 選擇賣出對其來說是最好的策略。

總的來說，在機構(gòu)投資者1 與機構(gòu)投資者2 都不知道對方的決策，且機構(gòu)投資者2 的股票份額大于機構(gòu)投資者1 的股票份額時，機構(gòu)投資者1 的決策與市場的關(guān)系不大，與機構(gòu)投資者2 的決策有關(guān)。對機構(gòu)投資者2，它的投資決策取決于市場股票價格波動的幅度，雖然它可以操縱股票價格的上漲或下跌，但是漲幅是難以控制的。

(2)當(dāng)q1＞q2時

若機構(gòu)投資者1 選擇買入，則機構(gòu)投資者2 選擇買入對其來說是最好的策略；若機構(gòu)投資者1 選擇賣出，則機構(gòu)投資者2 選擇賣出對其來說是最好的策略。

若機構(gòu)投資者2 選擇買入，則需要比較機構(gòu)投資者 1 買入和賣出策略收益的大小，即比較(p＋1-p)q1與(p-p-1)q1的數(shù)量關(guān)系；若機構(gòu)投資者2選擇賣出，機構(gòu)投資者1 的策略選擇與前面情況一樣。

比較(p＋1-p)q1與(p-p-1)q1，即比較p＋1-p與pp-1，也就是比較股票上漲價格和交易價格之差與股票下跌價格和交易價格之差的數(shù)量關(guān)系。 當(dāng)股價上漲幅度大于下跌幅度時，機構(gòu)投資者1 選擇買入；當(dāng)股價上漲幅度小于下跌幅度時，機構(gòu)投資者1 選擇賣出相應(yīng)的份額。

總的來說，在機構(gòu)投資者1 與機構(gòu)投資者2 都不知道對方的決策，且機構(gòu)投資者1 的股票份額大于機構(gòu)投資者2 的股票份額時，機構(gòu)投資者2 的決策與市場的關(guān)系不大，與機構(gòu)投資者1 的決策有關(guān)。對機構(gòu)投資者1，它的投資決策取決于市場股票價格波動的幅度，雖然它可以操縱股票價格的上漲或下跌，但是漲幅是難以控制的。

由以上q1＜q2和q1＞q2情況下，支付函數(shù)的分析對比，我們可以得知，只要該機構(gòu)投資者有足夠多的資金，不論選擇哪種策略都可以獲利；而相比之下資金不夠充足的一方就會受制于資金充足的一方。

第二階段:經(jīng)過上一階段的博弈，投資雙方可以得知對手的實力情況，此為公開信息。

假設(shè)3:機構(gòu)投資者2 具有一定的學(xué)習(xí)能力，在上一階段的博弈后，可以對機構(gòu)投資者1 的行為進(jìn)行預(yù)測。 而機構(gòu)投資者1 不具備學(xué)習(xí)能力，只能根據(jù)已有信息進(jìn)行決策。 機構(gòu)投資者1 的資金更加充足(q1＞q2)。

假設(shè)4:股價上漲幅度與下跌幅度一致，即p＋1-p＝p-p-1＝ Δp。

設(shè)機構(gòu)投資者2 以(a，1-a)的概率預(yù)測機構(gòu)投資者1 的行動，即它預(yù)測機構(gòu)投資者1 以a(0＜a＜1)的概率買入股票，以1-a的概率賣出股票。

此時存在一個混合策略(a，1-a)，單獨分析在該種情況下，機構(gòu)投資者1 與機構(gòu)投資者2 的支付函數(shù)。

當(dāng)機構(gòu)投資者2 買入時，

由此我們可以得到機構(gòu)投資者1 與機構(gòu)投資者2 的支付矩陣。 (表2)

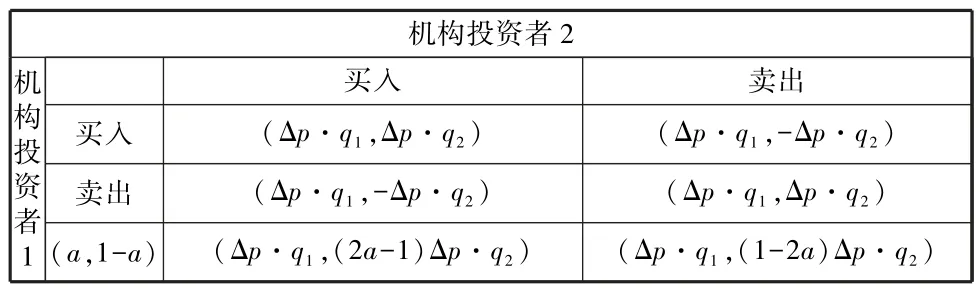
表2 機構(gòu)投資者1 與機構(gòu)投資者2 第二階段支付矩陣

對(a，1-a)的混合策略，當(dāng)a＞1/2 時，機構(gòu)投資者2 選擇買入；當(dāng)a＜1/2 時，機構(gòu)投資者2 選擇賣出。 但在資本控制的股市下，選擇資金雄厚的機構(gòu)投資者更為可靠。 (a，1-a)的混合策略對支付結(jié)果進(jìn)行了改進(jìn)，在一定概率下減少了自身的損失，回撤率在可控范圍內(nèi)即為占優(yōu)策略。

此階段是在股價上漲幅度與下跌幅度一致情況下進(jìn)行的分析，此處只是為了簡化模型而做出的假設(shè)。 在實際股票市場中，股價上漲和下跌的幅度很難把控，所以資金雄厚的機構(gòu)若想得到收益上的改進(jìn)，也必須考慮對手的決策，因為操盤也存在一定的風(fēng)險。 此模型的均衡解有兩種可能，機構(gòu)投資者同時選擇買入或者賣出，但具體情況下，均衡解為這兩種可能之間的一個，很難同時存在兩個均衡解。

現(xiàn)實情況下，小機構(gòu)投資者在沒辦法確定大機構(gòu)投資者決策時，不會選擇與大機構(gòu)投資者申購?fù)恢还善保瑫x擇繞開大機構(gòu)投資者與同類型的機構(gòu)投資者之間進(jìn)行博弈。

模型改進(jìn):第二階段可以改進(jìn)為博弈雙方得知對手的實力情況，此為公開信息。 即博弈雙方的實力相當(dāng)為公開信息，雙方都可以得知。 但其中一方具有一定的學(xué)習(xí)能力，在上一階段的博弈后，可以對對方的行為進(jìn)行預(yù)測。 (表3)

表3 機構(gòu)投資者1 與機構(gòu)投資者2 第二階段改進(jìn)支付矩陣

在考慮(a，1-a)的混合策略時，我們假設(shè)雙方的策略是(賣出，買入)或(買入，賣出)時的收益為0(即a1＝a2＝b1＝b2＝0)，便于分析(a，1-a)混合策略的收益情況。

當(dāng)雙方實力相當(dāng)時，(a，1-a)的混合策略可以起到止損的效果。 從支付矩陣中可以看出還是雙方?jīng)Q策一致時的收益更高，所以一方具有的學(xué)習(xí)能力只能幫助自己避免最差的決策。 在A 股市場，這種情況的均衡是相當(dāng)不穩(wěn)定的，機構(gòu)如果僅依靠從散戶身上謀取盈利，這樣的盈利是相當(dāng)?shù)偷摹?A 股市場的現(xiàn)狀是，散戶的個數(shù)不是很龐大，相應(yīng)的中國市場對風(fēng)險的畏懼，所以散戶投入的資金也不是很多。機構(gòu)一方能夠洞悉散戶的心態(tài)，與個別散戶形成一個新的聯(lián)盟，擴大自己的資金鏈，從而扳倒競爭的另一方來獲取高額的收益。

三、 博弈分析和研究展望

(一)博弈分析

在第一階段的不完全信息靜態(tài)博弈下，機構(gòu)投資者雙方都不知道對方的決策時，資金不夠充足的機構(gòu)投資者的決策與市場的關(guān)系不大，與資金充足的機構(gòu)投資者的決策有關(guān)。 對資金充足的機構(gòu)投資者，它的投資決策取決于市場股票價格波動的幅度，雖然它可以操縱股票價格的上漲或下跌，但是股票價格的漲幅是難以精準(zhǔn)控制的。 因此只要該機構(gòu)投資者有足夠多的資金，不論選擇哪種策略都可以獲利；而相比之下資金不夠充足的一方就會受制于資金充足的一方。

在第二階段的博弈下，仍然是不完全信息靜態(tài)博弈，但此時資金不夠充足的一方會觀察資金充足的大型機構(gòu)投資者的行動，并以一定的概率預(yù)測到對方的行動，根據(jù)預(yù)測的結(jié)果做出自己的最優(yōu)選擇[6]，由第一階段的分析我們可以得知雙方行動一致時，處于弱勢的一方才能獲得較好的收益，因此后行動的一方如果可以“追隨”對方的策略，可以獲得更好的收益。 在動態(tài)博弈下，此模型一般稱為斯塔克爾伯格(Stackelberg)模型。 先進(jìn)行股票交易的機構(gòu)投資者稱為“領(lǐng)導(dǎo)者”，后進(jìn)行股票交易的機構(gòu)投資者稱為“追隨者”。 從另一個角度來看，上述問題是一個序貫對策問題[7]，可以通過逆向歸納法進(jìn)行模型的結(jié)果的求解。

在兩階段的靜態(tài)博弈研究中，機構(gòu)投資者之間行動不分先后，只是一方具有一定的學(xué)習(xí)能力，能夠預(yù)測另一方的行動。 但在動態(tài)博弈下，如果后行動者能夠觀察到先行動者行動的情況下，該動態(tài)博弈模型即為序貫博弈，通過逆向歸納法，若“跟隨者”觀察到“領(lǐng)導(dǎo)者”的行動時，可以選擇跟隨還是不跟隨，根據(jù)本文模型的結(jié)果可以得知，選擇跟隨是該序貫?zāi)Ｐ偷木饨狻?此時機構(gòu)投資者之間面臨的問題就是如何公平合理地分配利益，從而使得這種默契能夠延續(xù)下去，此種均衡在A 股市場是相當(dāng)不穩(wěn)定的。 當(dāng)博弈雙方之間差距不是很大時，對背叛這種“默契”存在“觸發(fā)策略”，此時該一次性序貫?zāi)Ｐ涂梢詳U展為重復(fù)博弈。

(二)研究延伸和展望

本文研究的是A 股市場中機構(gòu)投資者之間的博弈，但是若把其中處于弱勢一方當(dāng)作“散戶”即個人投資者，可以得出一致的結(jié)論。 “散戶”只有跟對“莊家”才能避免成為股票市場上的“犧牲者”。 當(dāng)機構(gòu)投資者間的實力并沒有很大差距時，需要雙方對市場的敏感度比較高，只有此時才能更有可能達(dá)成“默契”。 此外，“莊家”也不能利用自身的信息和能力的優(yōu)勢為所欲為，要試探市場的平衡點。 操盤也存在一定的風(fēng)險，即“莊家”若不能做好充足的準(zhǔn)備可能面臨操盤的失敗。

本文研究的是機構(gòu)投資者之間的博弈分析，同時也對此博弈分析進(jìn)行了擴展和延伸，簡要分析了整個股市的基本情況。 后續(xù)的研究則需要探討更加嚴(yán)謹(jǐn)且更加符合股票市場的假設(shè)，對本文的模型進(jìn)行提煉和使用數(shù)學(xué)化的表達(dá)。 在此基礎(chǔ)上對本文的模型進(jìn)一步擴展，研究一次性序貫博弈下利益如何公平合理分配和重復(fù)博弈下的均衡解。