深度學習視角下初中物理高效復習策略*
——以“有關浮力大小的定性分析與定量計算”教學為例

林 軍 苗毓亭

(1.合肥市包河區教體局教研室 安徽合肥 230051)(2.合肥市第四十八中學濱湖校區 安徽合肥 230061)

一、問題提出

在當下初中物理的復習備考過程中，部分教師在習題講評課上往往只注重單純知識點的回顧以及解題過程與答案的講解，學生沒有真正理解題目中所涉及的物理知識的內在聯系，也沒有掌握其中蘊含的物理思想與物理方法。這種只注重“育分”而不注重“育人”的教學方法，導致學生解決問題的能力沒有得到真正的提升，因而復習效率不高。如何切實提高復習效率，培養學生的綜合素養和解決問題的能力，值得每位一線物理教師深思。筆者認為提高初中物理的復習效率的有效途徑是踐行深度學習。下面基于深度學習的理論，以典型的浮力問題的定性分析與定量計算為例，談談初中物理高效復習的策略，供同人參考。

二、深度學習的含義

深度學習不是增加學習難度的意思，而是指在教學過程中，教師設法創設有一定挑戰性的學習問題或學習任務，引導學生全身心積極參與，讓學生經歷知識獲取的過程與體驗，注重對知識的理解與建構，從而掌握學科的核心知識與思維方法，使學生能夠將所學的知識遷移到新的問題情境中，通過自主分析歸納，靈活運用所學的知識與方法解決實際問題。這是發展學生學科核心素養的重要方法與策略。

三、聚焦問題解決，踐行深度學習

在中考物理的復習備考中，部分教師往往“以師為本”，只注重自己講解問題的解決方法，剝奪學生深度學習的機會，久而久之，將導致學生的學科核心素養得不到發展。深度學習聚焦問題的解決，這就要求教師在學生學習的過程中設置關鍵性問題和挑戰性任務，不斷追問，引發學生深度思維，激發學生探究性學習的內在動力，真正地實現師生間基于問題解決的互動交流與深度的思維碰撞，培養學生的學科素養。

深度學習注重對知識群的理解，并非對單個知識點的碎片化理解，這就要求教師在學生學習的重點與難點上設置關鍵性的問題和挑戰性的任務，開展探究性學習，引導學生深度思維，迫使學生從“被動地聽”到“主動地想”的角色轉變。在教學過程中，教師一定要設法通過問題引領和任務驅動真正實現師生實時的深度交流和思維碰撞。初中物理中有關浮力知識的定性分析和定量計算是教學中的重要內容和中考物理的重點考查內容，也是初中物理中的一個教學難點。大部分學生在解決相關浮力問題時，往往憑自己的主觀臆斷做出判斷，通常錯誤率很高。那么在初中物理的復習教學中，如何引導學生學會分析物理過程，厘清各物理量間的內在聯系，理解物理本質，建構正確的物理模型，并應用相關物理原理、物理公式進行定性分析和定量計算，培養學生的科學思維和解決問題的綜合能力？筆者以安徽中考真題中的兩道典型的浮力題為例探討深度學習視角下初中物理的高效復習策略，以饗讀者。

例1(2020年安徽中考23題) 某同學想測量一種液體的密度大小。他將適量的待測液體加入圓柱形平底玻璃容器里，然后一起緩慢放入盛有水的水槽中。當容器下表面所處的深度h1=10 cm時，容器處于直立漂浮狀態，如圖1(a)所示。容器的底面S=25 cm2，ρ水=1.0×103kg/m3，g取10 N/kg。

(1)求水對容器下表面的壓強；(2)求容器受到的浮力；(3)從容器中取出100 cm3的液體后，當容器下表面所處的深度h2=6.8 cm時，容器又處于直立漂浮狀態，如圖1(b)所示，求液體的密度大小。

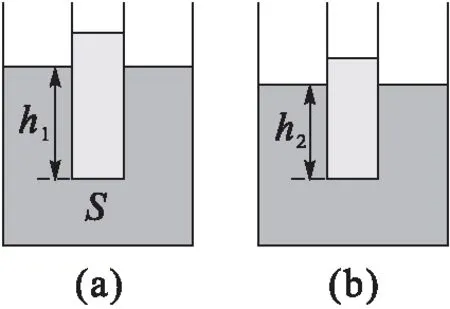
圖1

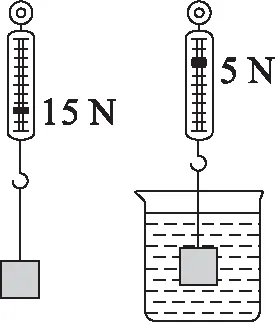
圖2

例2 如圖2所示，某物塊用細線系在彈簧測力計下，在空氣中稱時示數是15 N，浸沒在水中稱時測力計示數是5 N，則此時物塊受到水的浮力為N，該物塊的密度為kg/m3。

在隨堂聽浮力復習課時，一些老師對于以上兩題的解法通常如下。

例1：部分老師直接告訴學生浮力減小量和取出液體的重力大小相等，有學生追問老師這兩個量為什么相等。對于這個具有挑戰性的問題，很多老師為了節約時間，通常就自己分析講解解題的思路與方法，或者直接告訴學生二者相等的原因，沒有給學生提供分析推理和問題解決的機會，也沒有凸顯“以生為本”的新課程教學理念。

例2：一些老師要求學生求出待求物體的體積，然后再利用密度的定義式進行計算，這樣學生就要花較長時間來計算且計算錯誤率較高。這種教學方法與策略固化了學生的思維，阻礙了學生綜合素養的發展，也直接導致教學效率低下。

筆者以深度學習理論為指導，以發展學生科學思維能力為核心，設計合理巧妙、循序漸進的物理情境和物理問題，引導學生在其已有的認知、思維、情感等基礎上，不斷挖掘出認知復雜性層次更高的“問題鏈”，積極主動建構知識結構，厘清解題思路，進行科學推理，找出其規律，歸納得出最優的解題方法，進行深度學習。這樣不僅發展了學生的學科素養，而且提高了復習課的教學效果。

(一)分析對比，找共同點

表1是筆者引導學生對上述兩道中考物理試題，采用比較、歸納的思維方法，分析得出的共同點。學生很快便總結出所研究的對象都是處于平衡狀態，并提取出了有研究價值和意義的關鍵信息，構建知識結構，深化高階思維，為接下來的深度學習奠定基礎。

表1

(二)知識建構，分析推理

情境1：二力平衡

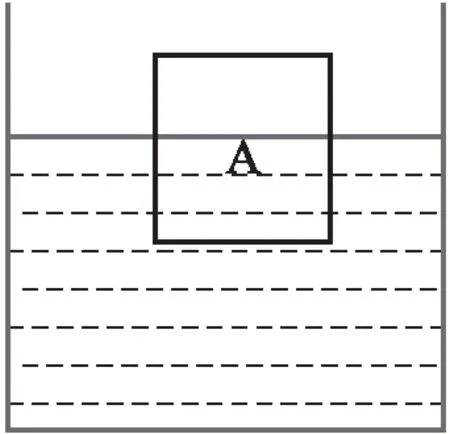
圖3

實際教學中，大部分學生能夠分析思考并歸納總結出方法如下：

建議在教學中，讓學生先獨立思考再分享自己的分析思路，教師則做好“引導者”，設法引導學生思考解決問題的突破口，并經過小組討論總結歸納出最優的解決方案。

具體思維過程如下：

已知：①力的關系：G物=F浮。②體積的關系：V物與V排。③ρ液。求：ρ物。

解題的突破口：厘清已知量和未知量間的內在聯系。

教師要引導學生學會有條理地羅列出題目中涉及的物理量，再引導學生做對比分析，發現其規律，深度思考后得出物理量之間的內在關系。

物塊A和液體的密度關系不易直接得出，但是物塊A所受的重力大小和液體所施加的浮力大小關系可以直接分析得出，即從受力分析的角度去建立已知量“力”和待求量“密度”的間接關系。學生發現浮力和物重這兩個力都可以寫成密度、體積和g的表達形式，即:F浮=ρ液V排g；G物=ρ物V物g。

接下來，再引導學生思考發現這兩個表達式中只有一個未知量，即待求量ρ物，關鍵就是怎么建立這兩個公式之間的關系。大部分學生很快便會通過受力分析得出結論。

已知F浮=G物，再推導出ρ液V排g=ρ物V物g，最后變形得出ρ物的表達式：

情境2：三力平衡

問題：在長方形容器的底部利用細線系著一個物重為6 N的木塊A，然后緩慢向容器中注水，使木塊A恰好浸沒于水中且保持靜止狀態，如圖4所示。此時細線對木塊的拉力為4 N，則木塊A的密度大小為kg/m3。

圖4

(1)定性分析

狀態分析：木塊A處于浸沒狀態，處于平衡狀態。

受力分析：木塊A受到重力、浮力和拉力。

在實際解題時，一般會遇到如下兩種情況。

學生通過深度分析思考，便不難發現上述題目中所蘊藏的共同點和不同點，采用“比值法”最終建立起“待求量”密度與“已知量”體積或者力之間的直接關系，從而減少了諸多中間量的繁雜計算過程。這樣的教學方法與策略培養了學生的科學思維能力和解決問題的能力，促進學生進行深度學習，落實學科核心素養的發展。

四、結語

綜上所述，在深度學習中，學生由被動的問題回答者轉變為高質量問題的主動提出者，從過去被動地聽轉變為積極主動地想的學習狀態，從淺顯的師生對話轉變為多角度的深度思維碰撞，從簡單的獲取知識轉變為能力、方法、思維和態度等的綜合培養。教師在教學中要設法創設真實的問題情境，注重引導學生對知識的遷移與應用，促使學生進行深度學習；同時在教學過程中，要設法摒棄“以師為本”的做法，始終凸顯學生的主體地位；設法提高學生的參與度，調動學生學習的主動性和積極性，提高復習課教學的質效。