基于穩健方差分析的多重與多元線性回歸模型比較
——以美國共享單車公司CapitalBikeshare為例

劉佳侖

（首都經濟貿易大學 北京 100026）

一、數據集介紹及數據預處理

本文以美國華盛頓特區的共享單車公司CapitalBikeshare，在2011—2012年間所記載的數據為目標數據集，選取當天是否為工作日、所處季節、天氣狀況、氣溫、體感溫度、濕度、風速這七個關鍵指標作為解釋變量，探索其與每日臨時用戶數量、注冊用戶數量、用戶總量之間的關系。對所選變量的具體說明如表1所示。

表1 所選變量及相關信息

接下來做數據預處理。首先，將數據集中tmp、atmp、hum、windspeed的標準值還原為實際值；其次，刪除2011年3月10日的異常數據，因為這一天的hum值顯示為0，實際生活中不可能出現這樣的情況；最后，為避免建模時出現多重共線性的情況，對含有兩個以上值的定性變量season和weathersit分別進行獨熱編碼處理，對應轉化為3個和2個啞變量。其中，將weathersit轉化為2個啞變量，是因為它的實際取值中并沒有出現過（大雨、大雪、大霧））極端天氣。

二、多元與一元方差分析

（一）多元單因素方差分析

做多元單因素方差分析時有兩個假設前提，分別為待檢驗總體的多元正態性和方差—協方差陣的同質性。前者可用Q-Q圖來進行檢驗，對于后者本文采用似然比檢驗。

1.多元正態性檢驗

多元向量的Q-Q圖通過展示卡方分布理論值與樣本值的關系，來判別待檢驗總體是否滿足正態性假設。如果所有點都落在斜率為1、截距為0的直線附近，則認為正態性假設成立。應用R軟件，得到響應向量（casual,registered）針對三個因素workingday、season、weathersit的Q-Q圖如下。

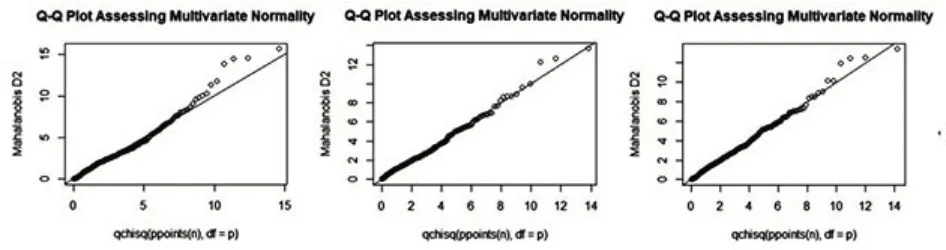
圖1（casual,registered）的Q-Q圖

結果顯示，響應向量（casual,registered）在不同因素下均服從多元正態分布。

2.協方差陣同質性檢驗

本小節中，響應向量（casual,registered）將針對三個因素workingday、season、weathersit分別做三次似然比檢驗，以驗證待檢驗總體協方差矩陣的同質性假設。

這里以workingday為例來說明檢驗流程。首先，應用R軟件的str函數來查看workingday在不同水平下響應向量的數據條數，所得結果記為n0=231，n1=499。將組別0和組別1中響應向量的數據矩陣分別記為Z0和Z1，在正態性假設下有Zi～Nni*q( )μi,Ini?Σi(i=0,1)。然后構造冪等矩陣，令其中1ni為全1列向量，于是有根 據 冪 等 矩 陣 性 質 可 得，Ui=其分布為且在U0和U1之間相互獨立。

所檢驗的問題為：H0:Σ0=Σ1v.s.HA:Σ0≠Σ1；似然比檢驗統計量為：

表2 似然比檢驗結果

各檢驗統計值均大于相應原假設下卡方分布上的0.05分位數。因此，在0.05的顯著性水平下拒絕原假設，認為針對上述三個因素進行多元方差分析時，協方差矩陣同質性的檢驗均未能通過，即協方差矩陣不齊，于是后續采用穩健多元方差分析的方法繼續進行檢驗。

3.穩健多元單因素方差分析

若多元正態性或者協方差矩陣同質性假設不滿足，又擔心多元離群點，那么需考慮采用穩健的MANOVA檢驗，此方法可通過R語言rrcov包中的Wilks.test函數來實現。檢驗結果如表3。

表3穩健單因素MANOVA

根據表3，所檢驗的三個因素對應的p值均小于0.05，于是在0.05的顯著性水平下拒絕原假設，認為共享單車每日臨時用戶數量與注冊用戶數量所構成的響應向量，在工作日與非工作日之間、在不同季節之間、在不同天氣狀況下的均值，都存在顯著性差異。

（二）一元單因素方差分析

以共享單車每日用戶總數cnt作為響應變量，以workingday、season、weathersit作為影響因素，分別做一元單因素方差分析。由于此方法的相關研究已經非常普遍，故本文不再詳細闡述其檢驗步驟。檢驗正態性仍使用Q-Q圖；判斷方差齊性選用Bartlett檢驗。值得注意的是，當檢驗因素各水平總體難以滿足方差分析假設條件（獨立性、正態性、方差齊性）時，可采用克羅斯考爾和瓦里斯在1952年提出的Kruskal-Wallis穩健檢驗方法。

對假設前提進行檢驗，cnt在各因素下基本滿足正態性假設，并且除season外在其他因素下滿足方差齊性假設，故對season使用Kruskal-Wallis穩健檢驗。方差分析檢驗結果表明，在0.05的顯著性水平下，cnt在工作日與非工作日的均值不存在顯著性差異，在不同天氣狀況下的均值存在顯著性差異，在不同季節的均值存在顯著性差異。

三、多元與多重線性回歸模型的建立

構建多元線性回歸模型，以casual和registered作為響應向量，以workingday、season_1、season_2、season_3、weathersit_1、weathersit_2、temp、atemp、hum、windspeed作為解釋變量；構建多重線性回歸模型，以cnt作為響應變量，其解釋變量與多元線性回歸模型的設置相同。然后將分別對上述兩個模型進行估計、檢驗及修正，以達到最優。

（一）多元線性回歸模型

1.參數估計

設Y=(Y1,Y2)為casual和registered構成的響應向量，x=(1,x1,x2,…x10)為解釋變量，R為隨機誤差項。于是可構建多元線性回歸模型：

在上述模型中，β的估計量為的估計量為其 中n＝730為 總 樣本量，p＝11為x的列數，l＝2為β的列數。根據以上表達式應用R軟件，即可輸出β和ΣR的估計值。

2.β中行參數的Hotelling’sT2檢驗

（1）提 出 原 假 設 與 備 擇 假 設：H0∶βi=0v.s.H1∶βi≠0

（2）應用R軟件，計算βi的F檢驗統計值。

表4 行參數的F檢驗統計值

3.模型修正

在原多元線性回歸模型的基礎上，剔除掉自變量atemp后，再做一次回歸，得到新模型中未知參數β′的估計值如表5。

表5 β′的估計值

對β′的行參數做Hotelling’sT2檢驗，得到行參數的F檢驗統計值如表6。

表6 行參數的F檢驗統計值

（二）多重線性回歸模型

1.參數估計及t檢驗

設Y3為共享單車每日用戶總數cnt，x同多元線性回歸模型，R為隨機誤差項，構建多重線性回歸模型：

應用R軟件的lm函數，得到β*的估計值及其各元素相應的t檢驗p值如表7。

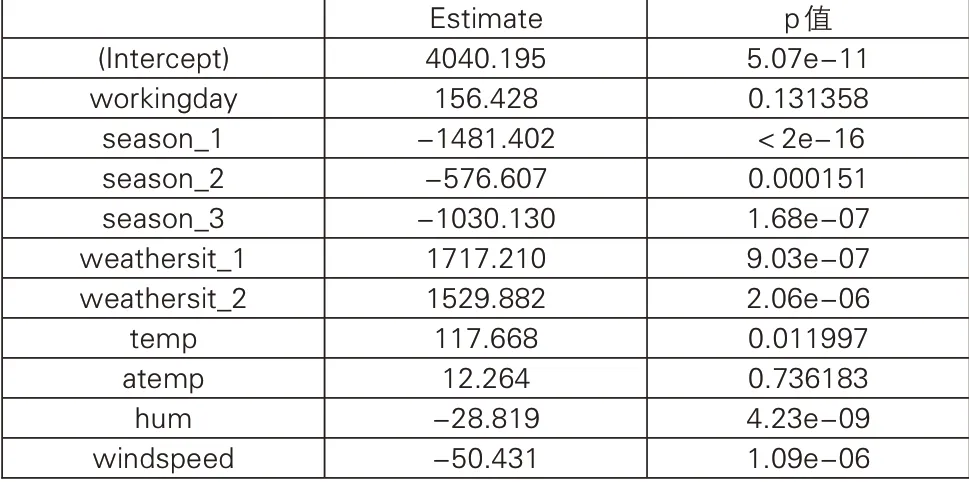
表7 β＊的估計值及t檢驗結果

當p＜0.05時，在0.05的顯著性水平下拒絕原假設，即認為相應的當p＞0.05時，在0.05的顯著性水平下不拒絕原假設，即認為相應的通過觀察表7可知，解釋變量workingday和atemp的參數均未能通過檢驗，于是需對此模型進行修正以達最優。

2.逐步回歸法修正模型

R語言做逐步回歸分析時，以赤池信息量AIC值的最小值作為確定最優模型的準則。采用逐步回歸分析方法對上述多重線性回歸模型進行修正，依次剔除解釋變量atemp和workingday，修正后的模型為：

cnt＝4125－1482season_1－581season_2－1049season_3＋1700weathersit_1＋1524weathersit_2＋134temp－29hum－51windspeed

R語言運行結果顯示：在修正模型中，每一個解釋變量對于響應變量cnt的線性影響都是顯著的。

四、結論

多元線性回歸和多重線性回歸對于沒有統計學背景的研究人員而言，確實是兩個非常容易被混淆的概念，通常會認為二者是等價的，但通過上文敘述，可以很明確地看出二者之間的區別與聯系。多重線性回歸（multiplelinearregression）是簡單直線回歸的推廣，研究的是一個因變量與多個自變量之間的數量依存關系。而多元線性回歸（multivariate linearregression）則是多重線性回歸的推廣，研究的是具有相關關系的多個因變量組成的響應向量，與多個自變量之間的數量依存關系。雖說從形式上來看，多元線性回歸模型是多重線性回歸模型的簡單疊加，但實際上，它的用途和研究意義都比后者更加廣泛。一方面它能夠衡量響應向量在不同維度之間的相關關系，另一方面它可以探究某一解釋變量對研究總體在不同維度的綜合影響。接下來，對兩類模型的構造方式和建模流程進行詳細的分析和對比。

在多元單因素方差分析部分，響應向量（casual,registered）針對三個因素workingday、season、weathersit均通過了顯著性檢驗，說明這三個因素對響應向量都具有顯著影響。于是在構建多元線性回歸模型時，應納入上述三個因素作為解釋變量，從表5呈現的信息來看事實也正是如此。一元單因素方差分析檢驗結果顯示，響應變量cnt在workingday各水平下的均值并無顯著性差異，但對因素season和weathersit都通過了顯著性檢驗，這與構造多重線性回歸模型時，不納入workingday但納入其余兩個因素作為解釋變量的事實相符。

綜上，無論多元還是一元方差分析結果，都與各自所構造的回歸模型相互驗證了彼此的正確性。另外，被解釋變量的維數設置體現了兩類回歸模型在構造方式上最明顯的差別，多元模型設置多維響應向量，多重模型僅設置一維響應變量。

在多元線性回歸部分，從表5可以看出，解釋變量workingday對臨時用戶數量具有負的線性影響，而對注冊用戶數量有正的線性影響，意味著工作日相比于非工作日，臨時用戶數量將減少，而注冊用戶數量增多。解釋變量season經分解后形成了代表春、夏、秋季的啞變量，對比冬季，春、夏、秋季的注冊用戶數量均呈現出負增長，春季和秋季的臨時用戶數量也呈現出負增長，但夏季的臨時用戶數量呈現出正增長，這表明夏季的臨時用戶數量比冬季更多。解釋變量weathersit經分解后形成了代表好天氣和較好天氣的啞變量，對比較差天氣，好天氣和較好天氣下的臨時用戶數量和注冊用戶數量均呈現出正增長趨勢。此外，在所設定的氣溫范圍內，溫度越高，臨時用戶數量和注冊用戶數量越多；在所設定的濕度和風速范圍內，濕度和風速水平越高，臨時用戶數量和注冊用戶數量越少。上述分析結果基本符合實際情況。

在多重線性回歸分析中，對比冬季，春、夏、秋這三個季節對每日用戶總數均呈現出負的線性影響，意味著春、夏、秋三個季節的每日用戶總數少于冬季。對比較差天氣，好天氣和較好天氣對每日用戶總數具有正的線性影響，意味著天氣越好每日用戶總數越多。此外，在定量解釋變量的研究范圍內，溫度越高，每日用戶總數越多；濕度、風速越高，每日用戶總數越少。以上內容基本與多元線性回歸的分析結果保持一致，但獲得的信息明顯少于多元模型。