新一代信息技術產業中企業研發投入影響因素研究
張汝飛,徐謝婷,趙 彤
(1.河北地質大學 經濟學院;2.自然資源資產資本研究中心,河北 石家莊 050031)
新一代信息技術產業是中國政府確立的戰略性新興產業之一,歷經“十三五”期間的成長壯大,其規模和龍頭企業數量已居各戰略性新興產業之首。“十四五”期間,中國政府更是指明新一代信息技術企業要持續向“數字產業化、產業數字化”方向取得新進步,加深傳統行業數字化規模、優化經濟結構、提高創新能力[1]。為了實現信息技術企業投資合理化、提升企業競爭力,本文通過二階段變量選擇方法,針對滬深兩市181家信息技術類上市公司的386個財務相關指標,篩選出影響企業研發投入的重要因素。
近年來,在變量選擇研究領域,Lasso、自適應Lasso(Adaptive Lasso,ALasso)、SCAD等懲罰回歸模型是較為常用的方法。當特征維度大于樣本量(即p>n),且在噪聲變量與重要變量相關的情況下,這些方法會保留更多的噪聲項,預測效果不盡理想[2]。因此,本文提出在高維普通最小二乘投影(Highdimensional Ordinary Least-squares Projection,HOLP)的基礎上,結合自適應Lasso(ALasso)的組合二階段模型以獲得更小的均方誤差(Mean Square Error,MSE),篩選出的變量用于描述企業研發投入更具代表性。
本文結構如下:(1)綜述高維回歸模型變量篩選方法的發展以及相關領域內的應用情況;(2)介紹HOLP-ALasso二階段變量選擇模型及估計步驟;(3)通 過 數 值 模 擬 比 較 基 于HOLP-Lasso、HOLP-ALasso、SIS-Lasso、FR-Lasso方 法 的 優 劣;(4)實證分析信息技術產業相關上市公司企業研發投入情況。
1 文獻綜述
在過去二十年中,國外有關高維數據的特征篩選方法已有大量研究成果,例如LASSO(Tibshirani,1996)[3],SCAD(Fan and Li,2001)[4],the Adaptive Lasso(Zou,2006)[5]等,但在變量個數p遠大于樣本量n時,上述方法在估計精度和計算效率上均難以得到保障。近年來,Fan等人(2008)提出確定獨立篩選法(SIS),該方法第一階段先對超高維數據進行降維,使得特征數降到樣本量之下(p 相比國外學者,國內更側重于應用層面。馮盼峰等(2018)研究基于隨機森林兩階段逐步變量選擇算法,第一階段確定變量重要性排名,第二階段進行逐步回歸,實證顯示該二階段算法相比于SCAD、Elastic Net具有較高預測精度[9]。郭林等(2020)提出兩階段判別的信用評價指標組合方法,ROC曲線的有效性檢驗表明基于二階段Logistic回歸的判別模型預測概率高,能有效區分企業的違約損失率[10]。郭宇瀟等(2021)提出一種排序和搜索策略的組合模型,將其結合不同機器學習方法,該模型篩選變量的準確度要優于偏最小二乘法-變量重要性投影(PLS-VIP)[11]。 綜上所述,國外針對p遠大于n的變量選擇問題,是將特征維度快速降至樣本量之下,再運用Lasso、SCAD等方法進行篩選;國內在變量選擇方面的應用主要集中于機器學習領域,鮮有Lasso、ALasso、SCAD等方法與二階段模型相比較的探索。因此,本文在Wang等人(2016)研究基礎上,提出利用ALasso進行二層過濾變量,并通過比較HOLPLasso、HOLP-ALasso、SIS-Lasso、FR-Lasso的 預 測誤差來評估組合模型的效果。 首先考慮線性回歸模型: Y∈Rn是響應變量,X∈Rn是設計矩陣,ε∈Rn是獨立同分布的誤差項,εi~N(0,σ2)。 假定當p>n時,XXT可逆,XTX不可逆,引入Moore-Penrose廣義逆處理Gram矩陣不可逆性。記全模型為M={x1,…,xp},真模型為MS,其中S={j:βj≠0,j=1,…,p}是基數為s=|S|的非零βj的指標集。為得到高維情況下篩選變量的方法,先給出β的一般線性估計類: A∈Rp×n把響應變量映射到估計值,在SIS中A=XT。 式(3)中Aε由零均值隨機噪聲項的線性組合組成,(AX)β是信號部分。在變量篩選的過程中要盡可能地保留信號變量部分,所以理想情況下的A將滿足條件AX=I。如果滿足上述情況,信號部分將會控制噪聲部分。顯然,當p 將變成普通的最小二乘估計。 但針對高維情況時,式(4)中的XTX是退化的,不滿足AX是單位矩陣的條件。Wang等人(2016)提出使用X的某種廣義逆:Moore-Penrose逆,令A=XT(XXT)-1。雖然在這種情況下AX不再是單位矩陣,但只要AX是對角占優矩陣,信號變量仍舊可以決定噪聲變量。 定義高維普通最小二乘投影的估計量: 即 式(5)的第一項可以將估計量看成β的投影。 HOLP選擇變量遵循的原則是對估計量β^進行排序并選擇其中最大項。確切地說,令d為篩選后保留預測變量的數量,有子模型Md如下: 或者 Chen(2008)提出的改進BIC準則(Extended Bayesian Information Criteria,EBIC)或直接挑選個變量均可確定HOLP的篩選數目[12]。 最小化式(7)確定子模型中的變量個數d,其中p為特征維數 Zou(2006)針對Lasso估計存在有偏性且不滿足Oracle性質而對L1懲罰項賦予了不同的權重,提出Adaptive Lasso,定義為: Zou(2006)指出用最優子集選擇解決OLS估計解釋能力弱的問題,但是模型不具有穩健性,微小的數據差異會引起較大偏差,降低預測精度;嶺回歸是一個連續的變量系數收縮過程,較為穩健,但是在擬合過程中沒有系數被估計到0,達不到變量篩選的目的;Lasso存在變量選擇不一致的情況,不具有Oracle性質,且估計是有偏的[5]。Adaptive Lasso解決上述模型中的問題,具有相合性及漸近正態性等性質,克服Lasso有偏估計的缺點,通過凸優化問題實現全局最優解。 HOLP的優點是具有確定篩選性質且計算過程高效,p>n情況下HOLP的計算復雜度為O(n2p)僅略次于SIS的計算復雜度O(np)[8];Wang等人(2016)發現HOLP的另一個優點是信號部分的尺度不變性,相比SIS可能會受縮放方式影響的缺點,HOLP更加穩定。在p>n時,HOLP中XXT矩陣總是滿秩的,這表現出在相同情況下比OLS更優的變量選擇。 Friedman(2010)提出沿正則化路徑計算的坐標下降算法(Coordinate Descent),處理高維數據的同時還可以保留模型中的稀疏特征[13]。第二階段基于Adaptive Lasso的凸優化問題保證用于求解Lasso的坐標下降算法可以同等效率地應用于Adaptive Lasso。具體步驟如下: (1)考慮第一階段HOLP子模型中估計量個數d。 1Md為示性函數。使用EBIC準則對估計量進行排序,選擇排序后的最大β^,剔除系數為0的不重要變量。 (2)應用基于坐標下降算法的Adaptive Lasso對β^進行二次處理。 懲罰參數λn由十折交叉驗證(N=10)確定。λn=據此選擇出系數不為0的變量為HOLP-ALasso最終篩選結果。 (3)評估不同二階段模型的擬合效果。設第t次在訓練集上的擬合值為,在預測集上的觀測數據為yt,定義評價指標MSE,MSE越小,模型預測精度越高,特征篩選方法更優。 在此通過數值模擬評估HOLP-ALasso等二階段模型預測效果,利用現有R包“glmnet”“screening”分析模擬數據篩選特征。本文參考Wang等人(2016)設置的模擬場景條件,結合實證研究的樣本數據,綜合確定所需樣本量和特征維數[8]。 考慮線性模型: 其中x=(x1,…,xp)是預測變量,具體分布形式見下文討論。樣本量n=200,特征數p=500,隨機誤差ε~N(0,σε2)。根據信噪比SNR=Var(xTβ)/σε2,分別探討SNR=50%和SNR=90%情況下計算得到的σε2,由模型形式生成響應變量y。具體而言,第一階段比較HOLP,SIS和FR等模型選擇正確模型的概率,已由Wang等人(2016)證明HOLP選擇正確模型的概率總體上要優于SIS和FR,能更有效地進行特征篩選。本文重點對比Lasso和ALasso第二階段模型擬合效果。考慮到特征之間的相關性對預測結果產生的影響,對自變量進行以下三種情況討論并設定具體參數值: 場景1:自變量x=(x1,…,xp)獨立同分布于標準正態分布N(0,1),令S={1,2,3,4,5},并將系數設定為: 場景2:自變量x=(x1,…,xp)服從多元正態分布N(0,Σ),協方差矩陣,其中ρ={0.4,0.6,0.8},將系數設定為: 場景3:自變量x1,…,x15構造形式如下: 其中k=0,1,2,3,4且Zi~N(0,1),控制組結構強度的參數δ2={0.1,0.05,0.01},x16,…,xp獨立同分布于N(0,1),將系數設定為 以上三種場景各重復模擬T=100次,計算MSE判斷二階段變量選擇方法的優劣。 當(n,p)=(200,500)時,表1展示了三種場景下的模型均方誤差,第二階段ALasso總體上比Lasso具有更低的均方誤差,由于ALasso對Lasso系數的壓縮程度進行了調整,使其具有Oracle性質且保持Lasso的凸性,從而模型預測精度高于Lasso。模擬實驗表明ALasso的特征篩選效果優于Lasso,為探究二階段組合模型的優劣,一并與其余四種方法進行比對。 表1 模型均方誤差(MSE) 在SNR=50%的低信噪比情況下,基于二階段HOLP-ALasso的組合方法均優于HOLP-Lasso、SIS-Lasso、FR-Lasso;HOLP-Lasso僅 次 于HOLPALasso,而SIS-Lasso效果最不理想。由此可以明顯看到SIS的缺點,因SIS強烈依賴于重要特征與響應y之間有很強的邊際相關性,但在高維數據中,預測變量之間往往存在相關性,這很有可能將與特征高度相關的不重要變量選入模型,這在場景2中很好地體現了這一點。 在SNR=90%的高信噪比情況下,盡管所有方法都有了顯著提升,但HOLP-ALasso仍然保持整體的優良性。整體上來看,FR-Lasso與HOLPLasso效果相近,但在場景3中ρ=0.8時,FR-Lasso的表現優于HOLP-Lasso,這得益于FR能一步完成變量篩選,同時Wang(2009)證實了在高維環境下FR也能進行確定性篩選,但FR的計算成本顯著高于其他方法,考慮到計算的簡便性和效率,HOLP-ALasso仍然是效果最優的二階段組合模型。 根據數值模擬結果,應用HOLP-ALasso實證篩選影響信息技術產業上市公司企業研發投入的關鍵因素。數據來自于國泰安數據庫,包括2020年181家上市公司386個影響研發投入的財務指標,具體包括資產負債指標、利潤指標以及現金流量指標等8個方面,如表2所示。 表2 影響研發投入的財務指標 將數據以7:3劃分為訓練集和測試集,分別用上述6種方法在訓練集上擬合模型,并計算測試集上的均方誤差,具體模型評估結果如表3所示。可以看出,基于二階段HOLP-ALasso的均方誤差最小,預測精度為0.110,模型擬合效果最優。 表3 模型評估結果 HOLP-ALasso最終從386個特征中篩選出9個變量,具體變量名見表4,其中有形資產帶息債務比與研發投入呈負相關,其余9個變量與研發投入呈正相關。觀察表4中的估計系數,管理費用、所有者權益和銷售收入增加額較大程度地影響了研發投入金額,而其余6個變量雖然系數較小,但作為篩選出的重要變量也對結果產生了不可替代的作用。 表4 HOLP-ALasso法篩選的變量和估計系數 本文研究高維數據下不同二階段模型的篩選效果,通過比較HOLP-Lasso、HOLP-ALasso、FRLasso等組合方法,證明HOLP-ALasso能有效選擇變量并且具有較高的預測精度,最后將該方法應用于新一代信息技術產業中企業研發投入影響因素的分析。 在數值模擬中,本文提出的基于HOLP-ALasso模型從整體上看具有最小預測誤差,相較于傳統Lasso、ALasso和 二 階 段HOLP-Lasso、SIS-Lasso、FR-Lasso,該方法能更有效的進行特征篩選。 此外,實證研究進一步驗證了HOLP-ALasso能篩選出變量個數少且與響應變量較強相關的特征子集。最終篩選出的9個指標表明信息技術類上市公司的利潤和盈利能力對企業研發投入產生較大的促進作用。企業在創新發展的道路上需要不斷提高盈利能力,可以關注以下兩個方面:一是緊跟市場需求,選擇自身具有競爭力且擁有較好市場空間的發展方向;二是在企業成長過程中,及時對經營模式做出調整,以更好地適應市場需求的變動。2 模型建立
2.1 基本假設




2.2 高維普通最小二乘投影(HOLP)
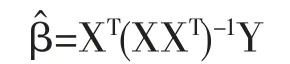
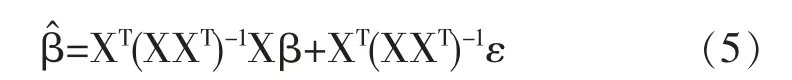


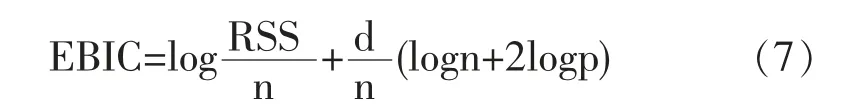
2.3 自適應LASSO(Adaptive Lasso)
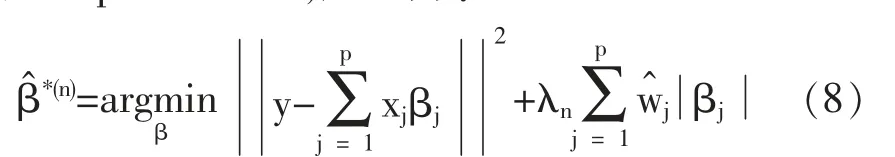
2.4 算法求解
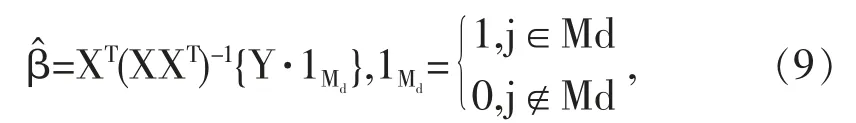

3 數值模擬
3.1 模擬參數設置


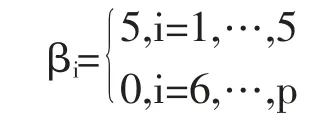
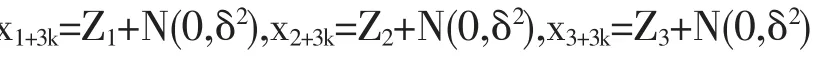
3.2 結果分析

4 實證研究
4.1 樣本選取

4.2 結果分析
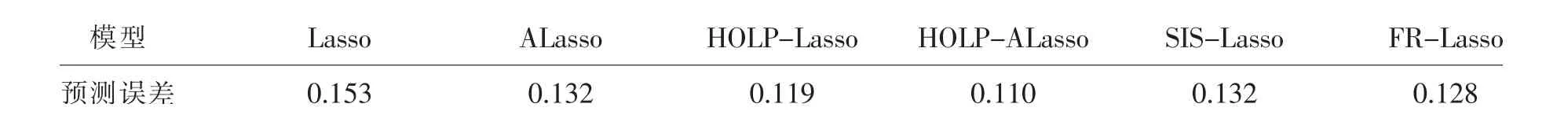

5 結論

