基于機器學習的回歸模型預測對比
宋敬茹 楊曉蕪
(華北理工大學礦業工程學院,河北 唐山 063210)
引言
為了預測各種類型的數據,大量學者嘗試建立相關的回歸模型[1],并對研究數據采用回歸方法進行分析,以節約獲取數據的時間、經費和人物力。然而,大多數方法主要集中在傳統線性回歸模型,如線性回歸和偏最小二乘回歸[2],但這些方法更適合于具有線性相關的參數變量[3]。
因此,近年來,機器學習因其更強大的靈活性和對數據的高度適應性而不斷發展和開始流行起來[4],在回歸分析方法上選取機器學習也變得逐漸活躍,如支持向量回歸(SVR)、隨機森林回歸(RFR)和增強回歸樹(BRT)。研究發現,SVR、RFR和BRT都能夠嘗試為各種類型的數據提供相當好的預測方法。Mountrakis等[5]通過研究發現,與傳統的線性方法相比,使用SVR算法可以降低回歸模型估計的誤差。Wang等[6]探究發現,RFR可以將決策樹與回歸分析模型的套袋算法相結合,其樣本選擇策略可以避免回歸的過擬合。同時,使用機器學習進行回歸分析已廣泛應用于許多數據預測相關領域,覆蓋面甚廣。因此,本文利用R軟件,采用SVR、RFR和BRT 3種機器學習對數據進行回歸建模的預測分析,并對回歸模型結果進行比較分析,選擇適合研究數據的最優機器學習回歸模型。
1 數據與方法
1.1 數據
本實驗采用數據來自中國國家氣象數據網(http://data.cma.cn/),共計66個國家基礎氣象站點樣本數據,并收集了對應所有氣象站點的經度、緯度和高程海拔數據信息。因數據量較大,無法全部展開,故只展示前30個樣本數據組,而全部66組數據均會作為本研究的實測值用以建立機器學習的回歸模型。為充分體現機器學習回歸模型的預測結果,建模數據基于新疆地區降雨量數據,因該地的特殊地理位置和氣候現狀使得降雨量數據存在明顯的差異,見表1。
為進一步建模做準備,對表1數據進行統計描述,見表2各個參數數據大致呈正態分布。通過對表1的數據進行統計分析,其中經度、緯度因地理位置變異系數最小分別為0.06和0.07,又因為新疆維吾爾自治區同時具有高原和盆地導致海拔方差最大為350427.84,海拔數據較為不穩定。同時發現4個參數的均值均滿足在95%置信區間內分布,因此本次回歸分析中4個參數均在可利用范圍內。
1.2 方法
1.2.1 相關分析
相關性分析是研究自變量和因變量之間關系程度的常用統計方法,以準確描述變量之間的相關性,相關系數大致包括3類,相關系數中皮爾遜系數[7]最常用于范圍廣泛的值,范圍在[-1,1],值在[0.8,1]或[-1,-0.8]表明其高度緊密相關;值在[0.5,0.8]或[-0.5,-0.8]表現顯著緊密關系;處于[0.3,0.5]或[-0.3,-0.5]的值表明兩者關系為實相關性;值處于[0.0,0.3]或[-0.0,-0.3]表明參數兩兩之間呈現微相關性,見表3。本文選取經度、緯度和海拔為自變量,降雨量為因變量,其相關系數的計算公式[7]:
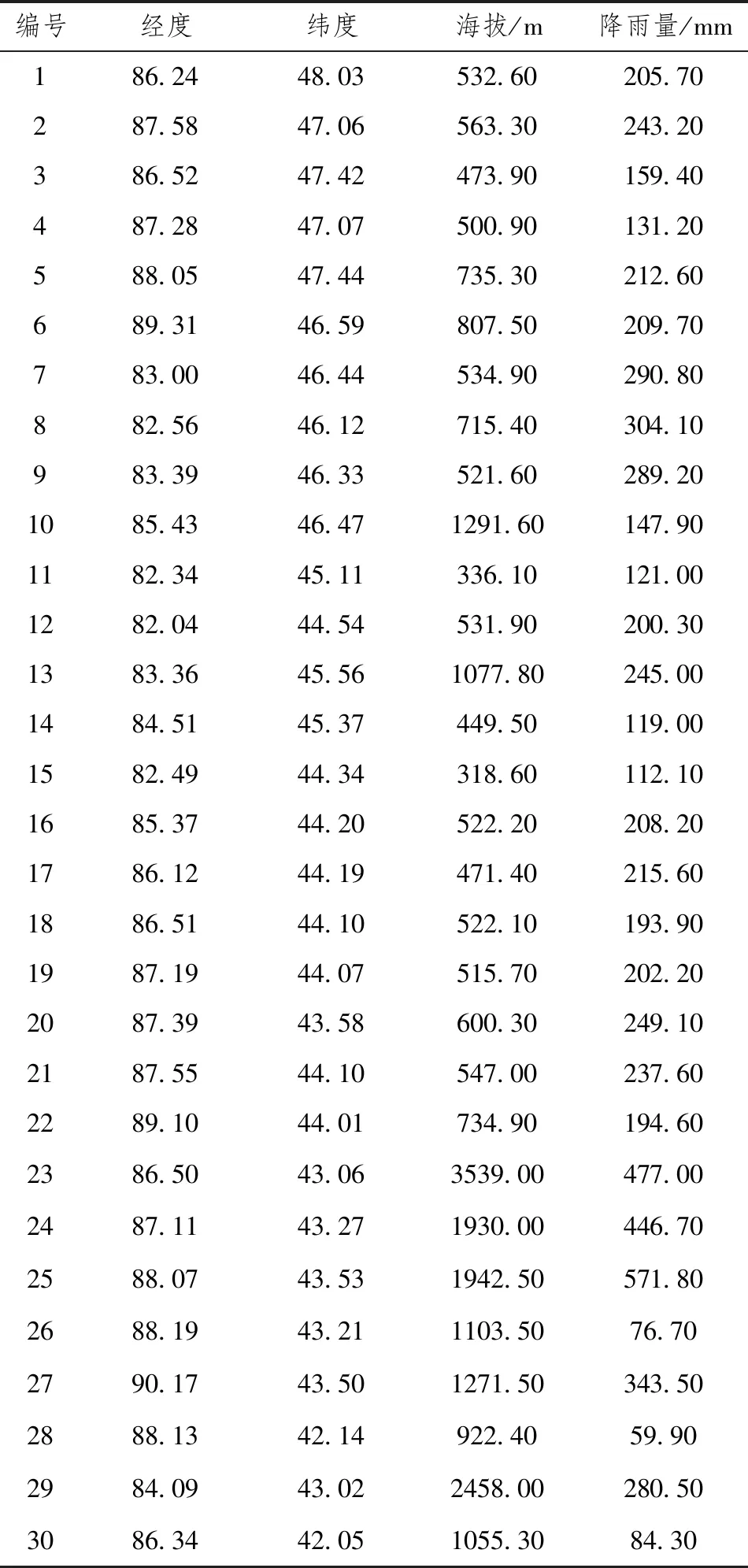
表1 回歸分析數據
(1)

1.2.2 機器學習回歸分析
1.2.2.1 支持向量回歸分析
近年來,支持向量機(SVM)在各種分類和回歸問題中的應用越來越多,在分類和回歸問題中均能得到較好的應用。支持向量回歸(SVR)是由支持向量分類(SVM)方法演變而來[8],SVR使用條帶來進行參數回歸擬合,其優點在于可以處理復雜參數關系,以高精度來不斷靠近呈現較為復雜非線性關系的數據[9]。通過調節超參數以期找到一個超平面,同時滿足從所有數據到此超平面的距離最小[10],且滿足于各個參數數據之間關系存在為非線性的情況。因SVR所具有的長處,其用于回歸分析獲得的結果顯著優于其它普通線性模型。
1.2.2.2 隨機森林回歸分析
隨機森林回歸(RFR)是一種統計算法理論,其是利用Bootsrap重抽樣方法從原始樣本中抽取多個樣本,對每個Bootsrap樣本進行決策樹建模,組合多棵決策樹的預測,并通過投票得出最終預測結果[11]。其中每個決策樹的建立都是一個隨機抽樣的過程[12]。在研究中采用自舉法,即通過抽樣獲得的樣本集中可能存在重復的樣本,可以有效避免過擬合,且具有較高的精度和泛化能力[13],RFR分析可以通過降低OBB error誤差值以獲取更優回歸結果。

表2 數據統計
1.2.2.3 增強回歸樹分析
增強回歸樹(BRT)是由眾多較短的決策樹(百棵以上)建立的,通過在梯度上減少殘差的模型,能夠在回歸分析法中不間斷的以遞歸形式分裂來消除眾多影響因子之間相互作用[14]。Boosting法用較短的回歸樹(tree)集合來表明與影響因子之間存在的非線性關系,BRT為解決單一決策樹面臨的缺陷,其隨機抽取并采用“梯度下降法”以降低回歸分析殘差,提升模型整體性能。在“梯度下降法”過程中tree的棵數逐漸遞增,模型的穩定能力和預測精度呈現顯著提升[15]。

表3 相關系數與相關程度關系
1.2.3 回歸分析評定指標
本文采用適合小樣本數據的留一交叉驗證法(LOOCV),從3個角度出發進行回歸分析評定,3個指標分別是擬合程度,即調整型決定系數(Adjusted-R2)、回歸誤差;均方根誤差(RMSE)和回歸模型穩定程度;相對分析誤差(RPD)。Adjusted-R2值高低表明擬合程度得優劣,RMSE值大小則闡明建立回歸分析的誤差的大小,RPD值所對應的穩定程度水平如表4。

表4 RPD值對應的穩定程度
(2)
(3)
(4)
(5)
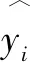
1.2.4 回歸分析框架
為了清晰直觀地說明研究過程,本文建立了一個基于機器學習進行研究的回歸分析框架,結合上述所有分析方法,系統化、全面化的對基于機器學習的回歸分析過程進行描述,見圖1。

圖1 回歸分析框架圖
2 結果
2.1 相關性分析
根據表1中樣本參數進行相關性分析,在表5各參數與降雨量相關程度分析結果中可以看出經度、緯度和海拔均滿足了p≤0.05的顯著水平,分析得出經度數據與降雨量數據的相關性較高為0.533*且呈現為顯著相關程度,而緯度數據與降雨量數據的相關性最低為0.377*,但也滿足了實相關,海拔數據與降雨量數據相關性為0.471*。

表5 參數與降雨量相關性分析
2.2 機器學習的回歸分析結果
基于3種機器學習算法并結合經、緯度和海拔等參數數據信息對降雨量進行回歸分析預測,產生的預測值的結果各有不同,3種算法回歸結果如圖2。通過觀察圖2可明顯發現,基于RFR算法的回歸分析能夠使得降水量的真實值和預測值更加接近1∶1線,即回歸結果較SVR和BRT的結果更優。
僅憑觀察圖2無法深切探究出3種機器學習回歸分析的最優預測結果,為更具清晰化地對比3種機器學習,故基于式(2)~(5)共3個指標全方位的對3種機學器習的回歸分析結果進行詳細對比,結果見表6。

表6 機器學習的回歸分析對比

圖2 3種機器學習的回歸分析結果圖
依據SVR算法回歸結果計算出的Adjusted-R2值為0.67,RMSE值為65.08,RPD值為1.80;RFR算法回歸結果中的Adjusted-R2值為0.92,RMSE值為32.35,RPD值為3.61;BRT算法回歸結果中的Adjusted-R2值為0.87,RMSE值為41.03,RPD值為2.85。綜上,RFR算法回歸結果的Adjusted-R2值最大,RMSE值最小,RPD值最高。由此可知,相較于SVR和BRT機器學習回歸結果,RFR算法回歸擬合效果最好、誤差最低以及穩定性最優,故3種機器學習對比而言,利用RFR算法進行回歸分析能取得更好結果。
3 結論
本文采取SVR、RFR和BRT 3種機器學習回歸模型對降雨量數據分別進行了預測分析,并對回歸分析結果進行全面評定對比。結果顯示,使用機器學習算法可以有效提高數據預測結果的準確性。就整體觀察而言,基于SVR、RFR和BRT 3種機器學習對降雨量數據進行回歸分析預測都取得了較好的結果,但利用回歸結果圖和Adjusted-R2值、RMSE值及RPD值進行綜合評定,發現RFR算法回歸結果明顯優于SVR和BRT結果,故最終選定基于RFR算法的回歸分析,且認為利用該算法能夠較好地對降雨量數據進行預測。RFR模型為數據量預測復雜等問題提供合理解決方法,達到高效預測數據的目的,與此同時對進一步深入探究回歸分析算法具有一定的參考價值。

