一種針對含非線性子結構多點耦合運輸包裝系統的解耦方法

王維凱，王軍，盧立新，潘嘹，侯雪

一種針對含非線性子結構多點耦合運輸包裝系統的解耦方法

王維凱1，王軍1，盧立新1，潘嘹1，侯雪2

（1.江南大學，無錫 214122；2.汕頭東風印刷股份有限公司無錫分公司，無錫 214000）

考慮到運輸包裝系統耦合形式復雜，包裝材料及包裝結構具有非線性特性，不容易測量局部物理參數，需要對傳統逆向子結構方法進行優化，使之能夠求解非線性多點耦合系統中子結構的動態響應特性。使用描述函數法將非線性的運輸包裝系統線性化，測量其在若干特定振動幅值下的頻率響應函數；之后，應用逆向子結構方法和參數識別方法，計算包裝件的模態參數；最后，擬合包裝件模態參數與振動幅值之間的關系，構建函數來描述包裝件的動態響應特性。在集總參數模型中，解耦預測值與實際值吻合；在有限元模型中，對響應峰值的預測誤差小于5%，對響應跳躍現象所在頻率的預測誤差小于3%。該研究將傳統逆向子結構方法的應用范圍拓展到了非線性多點耦合系統，對復雜運輸包裝系統動力學模型的構建和防振包裝的設計具有指導意義。

逆向子結構方法；運輸包裝；振動；非線性

在現代緩沖包裝設計流程中，設計師經常借助動力學計算和有限元仿真來確定緩沖材料和包裝結構的參數。其中，包裝件動態響應特性的獲取是精準有效建立其動力學模型的關鍵[1]，然而，在實際運輸過程中，產品、包裝與運載車輛耦合聯結在一起，構成復雜的運輸包裝系統，致使包裝件的動態響應特性難以被直接測量[2]。此外，包裝件在耦合狀態與非耦合狀態下的響應特性不同，對其單獨測量的結果不能代表其在耦合狀態下的特性。針對這一問題，王志偉、王軍等[3-6]將逆向子結構方法應用到了運輸包裝領域，實現了對運輸包裝系統中子結構動態響應特性的間接預測。

為建立與實際情況更加接近的理論模型，逆向子結構方法在近年來持續發展。主要趨勢有：為適應集裝、堆碼等復雜耦合情況，從單點耦合系統向多點耦合系統發展[7-8]；為重點考慮產品中的易損部件，從二級耦合系統向多級耦合系統發展[9]；設法降低誤差，如利用奇異值分解方法抑制計算過程中矩陣求逆導致的誤差放大[10-11]。

在以往研究中，均假設運輸包裝系統是線性的，而實際包裝材料與包裝結構具有非線性特性[12-14]，在使用傳統逆向子結構方法進行分析時，將非線性結構視作線性結構會導致求解結果不準確。對此，筆者在之前的研究中，結合逆向子結構方法與參數識別技術，實現了對含非線性子結構耦合系統的解耦，其中只考慮了單點耦合的情況[15]。文中結合運輸包裝實際，針對含非線性子結構的多點耦合系統做進一步討論，拓展了逆向子結構方法的應用范圍，并分別在集總參數模型和有限元模型中進行了驗證。

1 理論方法

包裝件與運載車輛之間的耦合關系見圖1a，該耦合系統可抽象化為圖1b所示的物理模型，文中以該模型為基礎進行理論分析。

1.1 非線性系統線性化

逆向子結構方法需要測量系統的頻率響應函數來進行解耦運算，而非線性系統不具備傳統意義上的頻率響應函數，因此需要將其線性化。

非線性結構的動力學方程可以寫成：

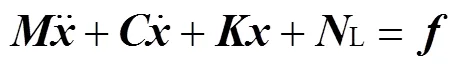
式中：、和為質量矩陣、阻尼矩陣和剛度矩陣；和L分別為外部激勵力向量和內部非線性力向量；為位移向量。

假設激勵是簡諧振動，根據歐拉公式，在時域上能被寫成：

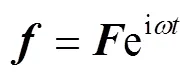
式中：為簡諧激勵的幅值；為激勵的角頻率；e為自然常數，i為虛數單位。

非線性結構的穩態響應以級數形式表示為：

式中：為結構的第階諧波響應；為第階諧波響應的幅值。通常，第1階諧波是響應的主要成分，而其他階次諧波相對較小[16]。在忽略高階諧波的前提下，式（3）可寫成：

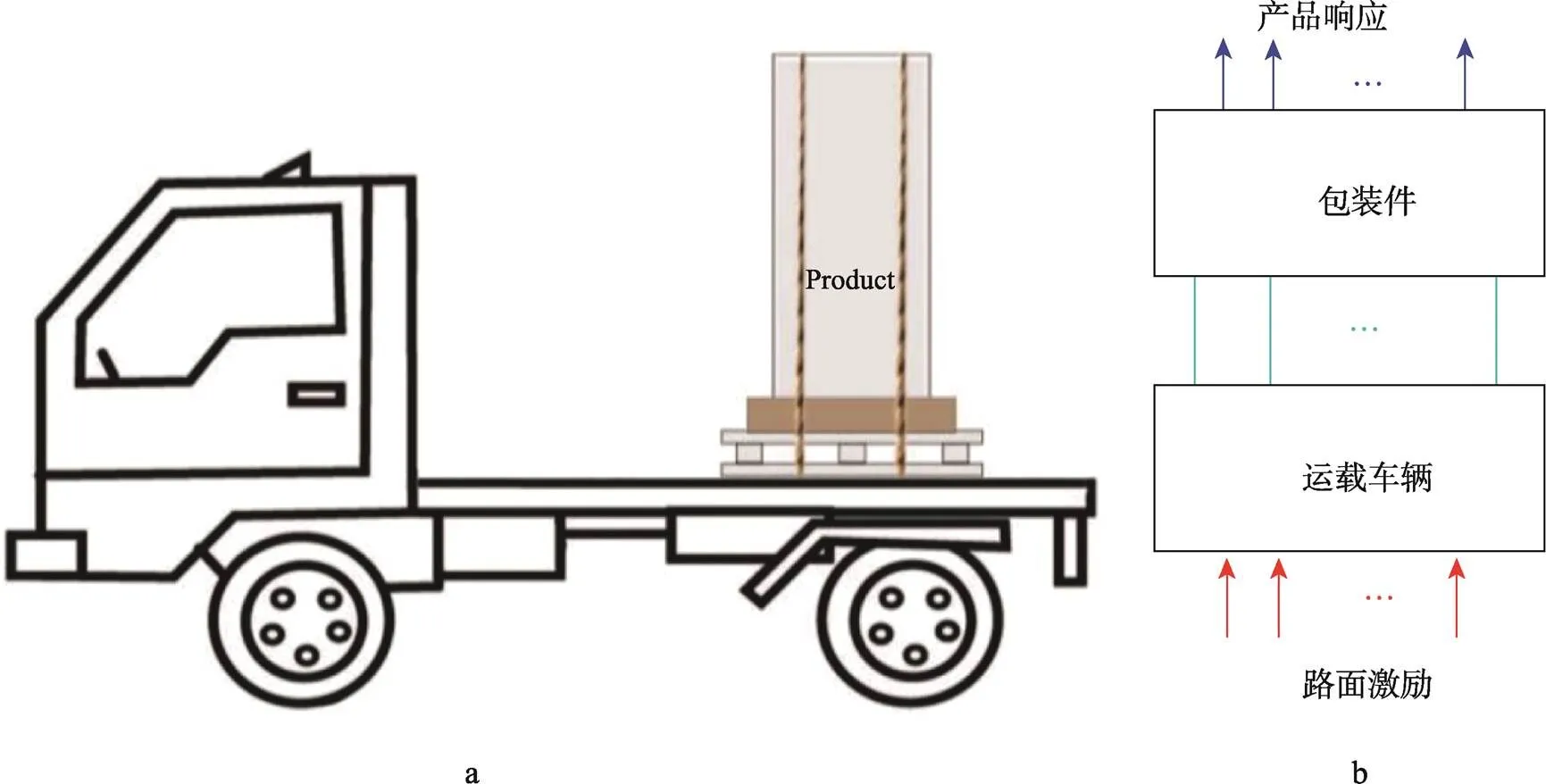
圖1 包裝件–運載車輛耦合系統

式中：為第1階諧波響應的幅值。與之對應地，非線性內力也只考慮第1階諧波，并設為第1階內部非線性力的幅值，得到：

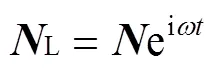
將式（2）、（4）和（5）代入到式（1）中，得到：

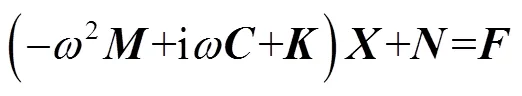
如果該結構的非線性特征體現為：剛度隨響應幅值的變化而變化。那么，根據描述函數法[16]，可以把非線性內力的幅值寫成響應幅值的一次函數，即：

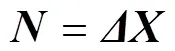
式中：為描述函數矩陣。矩陣內部各位置的元素為：

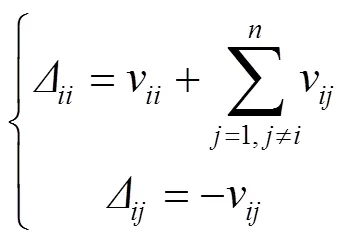
式中：Δ為位于矩陣中第行列的元素；Δ為位于矩陣中第行列的元素；v為結構中坐標和地面之間的非線性力的描述函數；v為結構中坐標和坐標之間非線性力的描述函數。v和v的值均與響應幅值有關，因此，是隨變化的函數。在此基礎上，式（7）能被表示成式（9）的形式。

其中：

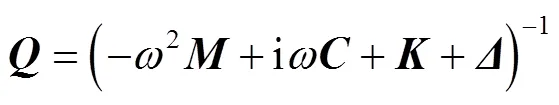
在文中被稱作準線性頻率響應函數矩陣，它的值與結構的振動幅值有關，只能表征結構在特定振動幅值下的響應特性。

至此，實現了非線性結構的線性化，得到了非線性結構的準線性頻率響應函數。

1.2 逆向子結構方法

將圖1所示的包裝件—運載車輛耦合系統抽象化，考慮一個由非線性子結構A和線性子結構B組成的系統S，見圖2。2個子結構之間通過對耦合點連接在一起。圖1中，a和b分別表示非線性子結構A和線性子結構B的內部自由度，a和b分別表示它們的耦合自由度，C為耦合剛度矩陣。

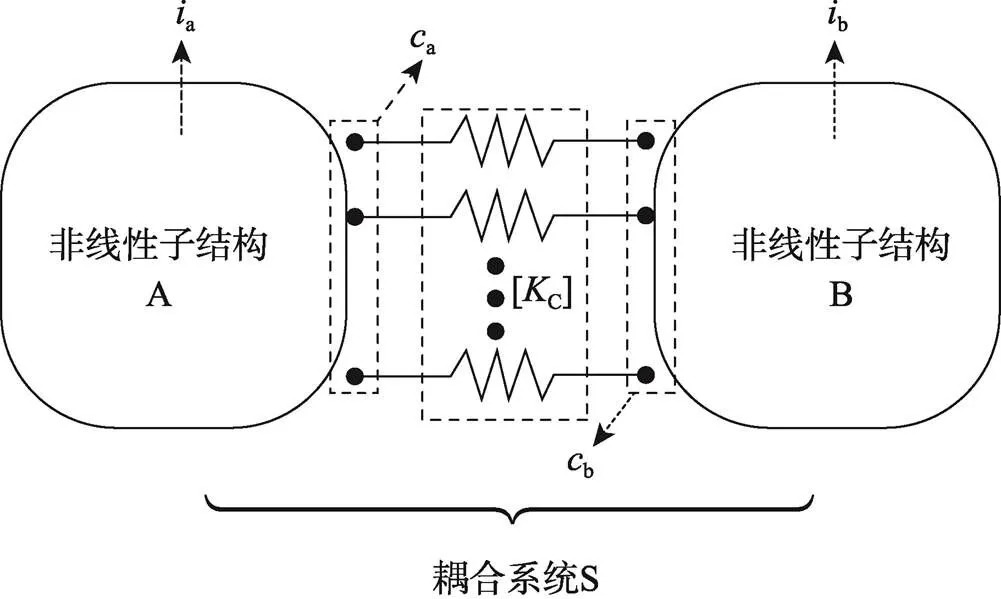
圖2 包含非線性子結構的多點耦合系統

其準線性頻率響應函數矩陣可表示為：

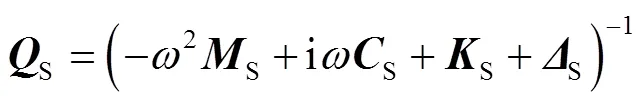
式中：S、S和S分別為系統S的質量矩陣、阻尼矩陣和剛度矩陣；S為系統S中以描述函數法線性化的非線性內力矩陣。S和S隨響應幅值變化。

系統S的動力學方程可寫作：

其中：

舉例說明式（13）中變量的物理含義：[S,iaia]表示耦合系統S中，自由度a的準線性驅動點頻率響應函數；[S,iaca]表示耦合系統S中，從自由度a到自由度a的準線性跨點頻率響應函數。

另一方面，根據力的平衡條件，可得：

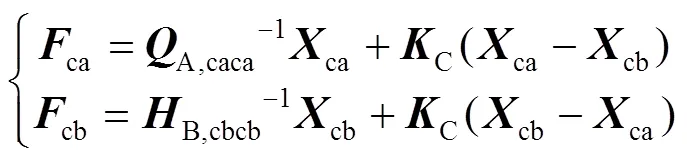
式中：[B,cbcb]為線性子結構B中，耦合自由度b的驅動點頻率響應函數。

結合式（12）、（13）、（14）可得到二級耦合系統的解耦公式：

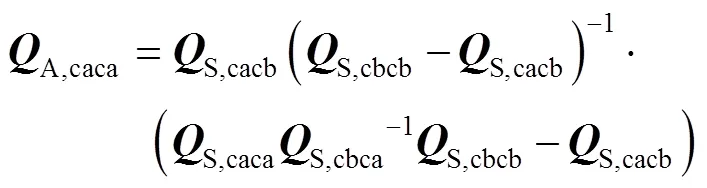
式（15）在本研究之前已有其他研究者得出，其含義是非線性子結構A的準線性頻率響應函數可通過對耦合系統S進行測量得出。

與單點耦合系統相比，多點耦合系統中的耦合坐標有個，因此，頻率響應函數矩陣中對應位置的元素為維矩陣。以兩點耦合系統（耦合自由度為a1和a2）為例，其耦合自由度的準線性頻率響應函數矩陣表示為：

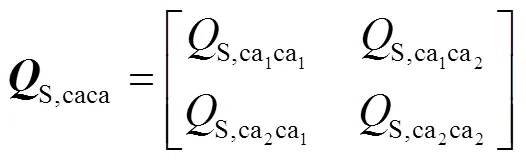
1.3 基于模態參數識別的響應特性求解

因為非線性系統的準線性頻率響應函數是在唯一固定的響應幅值下確定的，因此，由式（15）只能得到非線性子結構在特定振動幅值下的響應特性，而無法預測其在任意大小激勵下的響應特性。對此，提出一種基于模態參數識別的求解策略。

首先，使用激振器給系統施加種不同幅值的激勵，記錄非線性子結構中某點的響應幅值，測得系統在種不同響應幅值下的準線性頻率響應函數S(1),S(2), …,S()。之后，應用模態參數識別技術求解出對應于每個響應幅值的固有頻率和阻尼比。經此過程，會得到與響應幅值有關的一組固有頻率{n1,n2, ……,nm}和一組阻尼比{1,2, ……,}。最后，以作為自變量，分別擬合其與固有頻率n和阻尼比的關系，得到n()和()，兩者都是的函數。

對應于黏性阻尼系統頻率響應函數的模態表達式，將作為響應幅值函數的模態參數代入到頻率響應函數表達式中，可以重構出非線性結構關于響應幅值的頻率響應函數(,)，其表達式為：

式中：為所分析的模態數；nr為第階模態的固有頻率；ζ為第階模態的阻尼比；C()為第階模態頻率響應函數表達式中的常數項。

根據頻率響應函數的定義，有：

對式（18）進行求解，即可求得測量點在任意大小激勵下的響應。

2 模型驗證

2.1 集總參數模型

該節中，參考一般運載車輛的結構，建立了一個含非線性部件的集總參數模型，見圖3。通過對這個模型的分析，來驗證所提出解耦方法的可靠性。

該模型由非線性子結構A和線性子結構B兩部分組成。子結構A代表具有非線性特性的包裝件，子結構B代表運載車輛。其中，為集中質量，集中質量之間存在線性剛度和線性阻尼，它們的下標為不同位置參數的編號。在子結構A中加入一個非線性彈簧NL，以體現包裝材料和包裝結構的非線性，這使得子結構A成為一個非線性子結構，也使得整個系統成為一個非線性系統。2個子結構之間通過彈簧4和5、阻尼4和5，形成兩點耦合。模型中參數的值見表1。

下面說明如何在不拆解結構、只能在耦合狀態下激勵和測量的前提下，計算非線性子結構A的振動響應特性。

假設非線性彈簧NL具有立方剛度的性質，其非線性內力L表示為

式中：kNL的值為1×107 N/m3。

表1 集總參數模型中參數的值

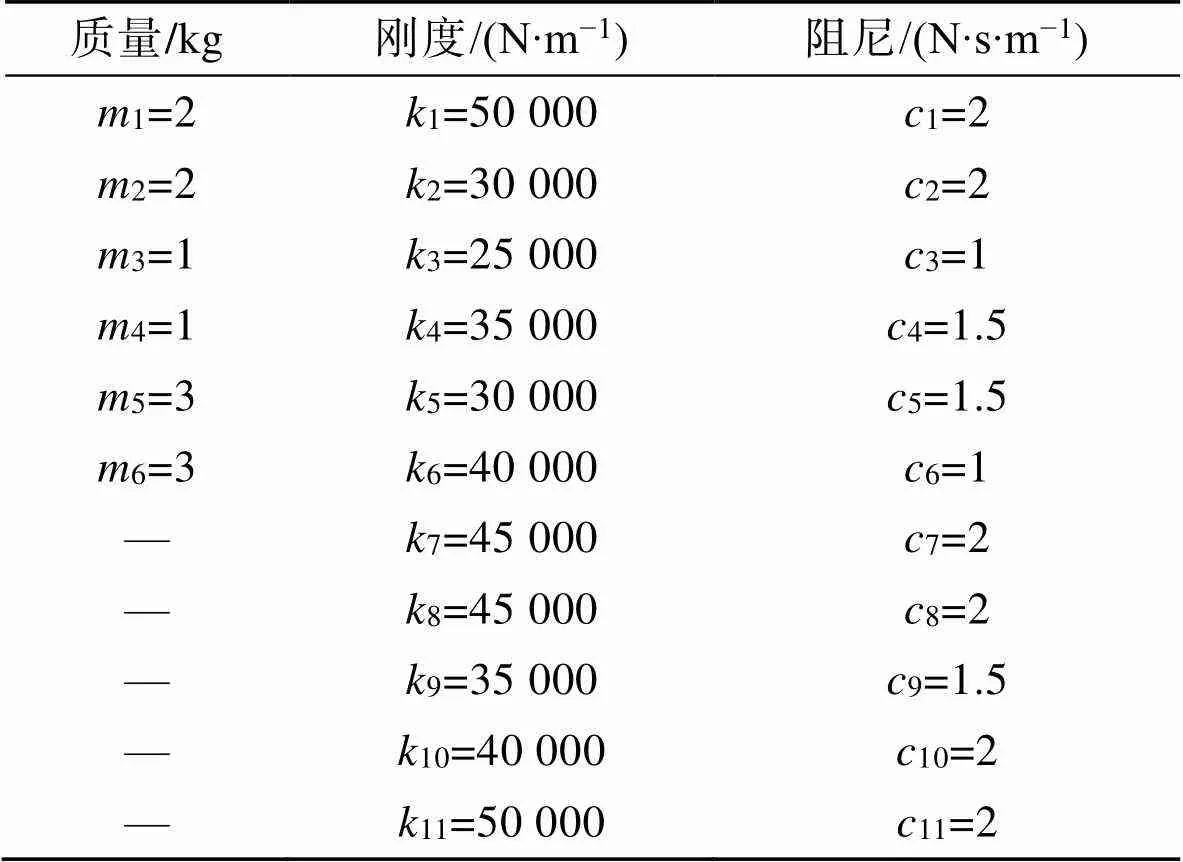
Tab.1 Parameters in the lumped parameter model

該系統的準線性頻率響應函數可由式（11）給出，其中：

控制1處的振幅從2 mm增加到20 mm，計算耦合自由度ca在不同振幅下的準線性頻率響應函數。以S,ca1ca1和S,ca1ca2為例，其部分響應特性見圖4，可見該結構的響應特性會隨響應幅值而改變，具有明顯的非線性特征。

類似地，分別計算出S,cacb、S,cbcb和S,cbca，將它們代入到式（14）中，可解耦得到非線性子結構A的準線性頻率響應函數A,caca，見圖5。可以看出，子結構A的一階固有頻率會隨響應幅值的增加而遞增，表現出漸硬的特性。

為檢驗該解耦方法的準確性，以非耦合狀態下的子結構A為對象，應用諧波平衡法直接計算1處驅動點頻率響應函數在若干振幅下的實際值，將其與預測值進行比較，結果見圖6，兩者保持高度一致。

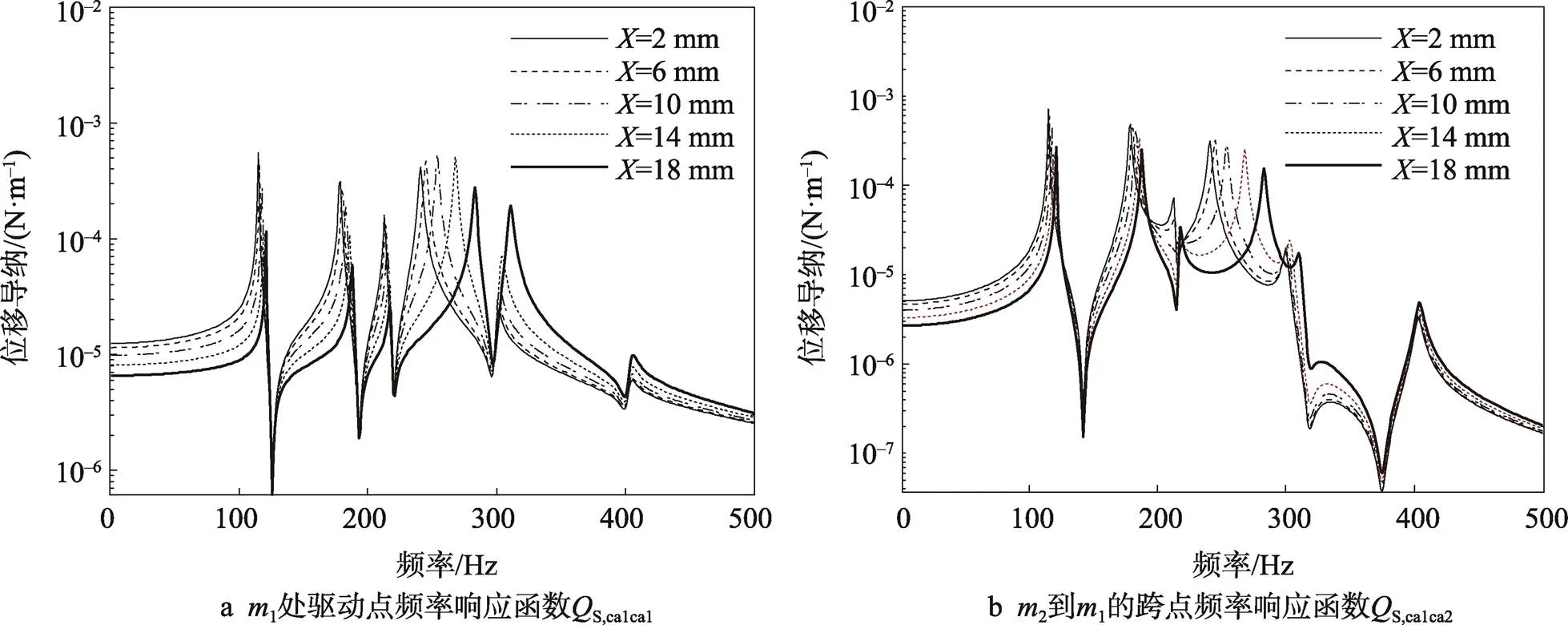
圖4 子結構A耦合自由度頻率響應函數在不同響應幅值下的測量結果

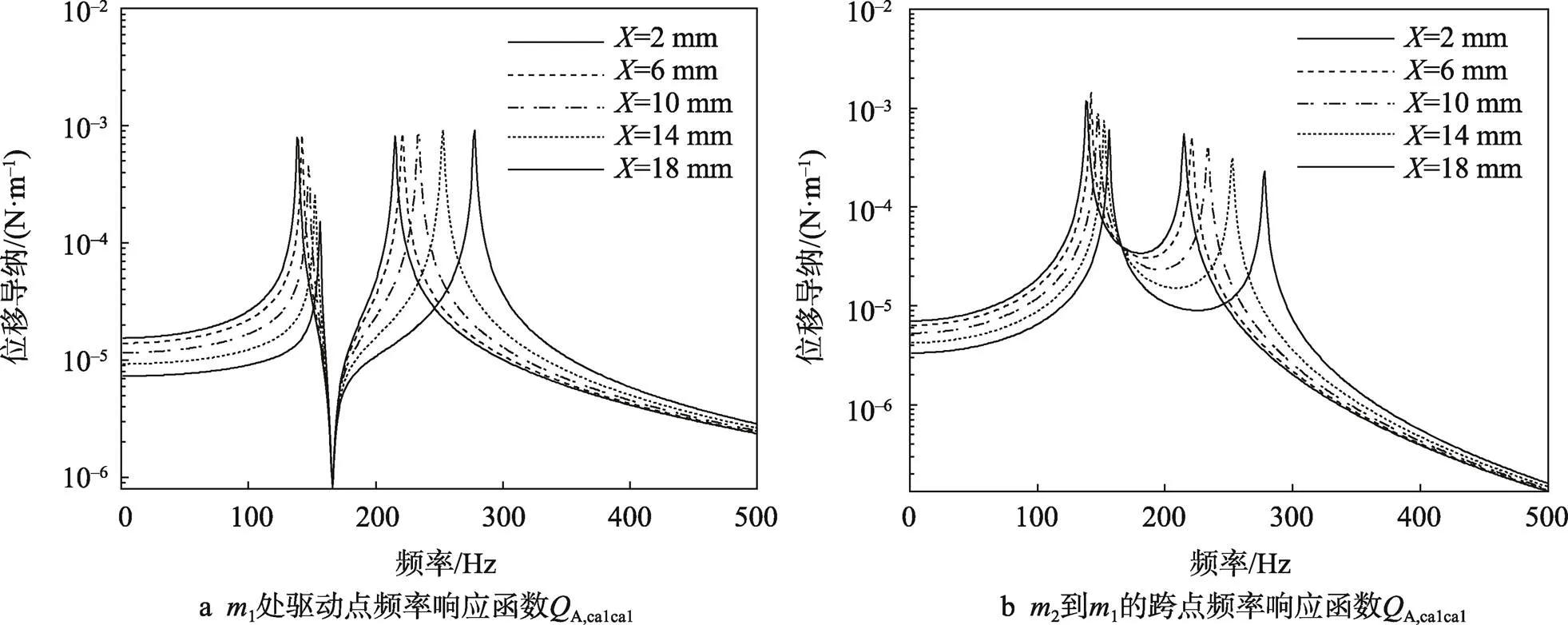
圖5 子結構A耦合自由度頻率響應函數在不同響應幅值下的解耦結果

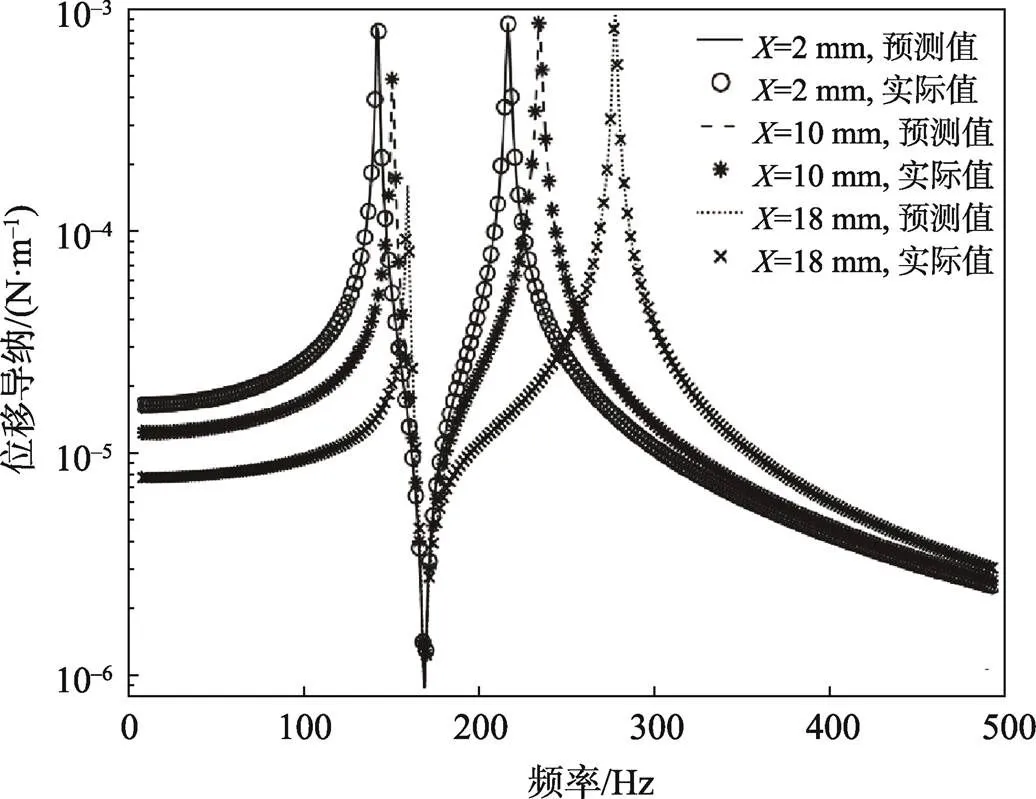
圖6 m1處驅動點頻率響應函數在不同響應幅值下的預測值與實際值對比

基于非線性子結構A的1處的驅動點頻率響應函數，應用多項式擬合法識別其模態參數，并擬合模態參數與非線性彈簧響應幅值之間的函數關系。將各模態參數作為振幅的函數代入到式（17）中，可以重構出式（21）函數來描述的1處的振動響應特性：

假設外部激勵F為20 N，而激勵的位移幅值不再固定，作用于m1處對子結構A進行正向掃頻，根據式（18）所給出的關系，即可對位移響應X進行求解，這里使用的求解方法為牛頓迭代法。解得m1處的驅動點頻率響應函數，并將其與理論值進行比較，結果見圖7。可見兩者高度一致，且精準預測了對非線性結構進行掃頻時出現的響應跳躍現象。

2.2 有限元模型

在此節中，建立了一個包含非線性子結構的多點耦合系統有限元模型，并通過對其進行頻率響應分析來檢驗文中所提出理論在連續體模型中的應用效果。該模型由一個具有線性剛度特性的懸臂梁和一個具有非線性剛度特性的T型梁通過2根彈簧連接而成，模型裝配效果及幾何參數見圖8。

圖8 包含非線性部件的多點耦合系統有限元模型及其幾何參數

文中所使用的有限元建模與分析軟件為ABAQUS。在軟件環境中完成建模后，設置如下材料參數與約束條件：構成懸臂梁和T型梁的材料均為鋼，其彈性模量為200 GPa，泊松比為0.3，密度為7 800 kg/m3。上方懸臂梁為線性子結構，在其固定端設置完全固定約束；下方的T形梁為非線性子結構，由一根懸臂梁和一根兩端固定薄梁剛性連接而成，在連接位置設置綁定約束，在其固定端設置完全固定約束。點與點、點與點之間各有一根剛度均為5 000 N/m的彈簧連接，通過設置彈簧連接器實現。

應用文中所提出的解耦策略，可以在不對模型進行拆解的前提下，通過測量該系統在4個耦合點的頻率響應函數，來預測非線性子結構（即T型梁）的頻率響應函數。利用有限元軟件對該模型進行模態分析，得到其一階模態的有效質量占結構實際質量的83.2%，因此可以判斷該模型的響應主要受一階模態影響，文中考慮其一階模態。

對系統進行激振，控制點的響應幅值分別為0.5、1、1.5、2、2.5、3 mm，測量每個響應幅值下各耦合點的準線性頻率響應函數，它們組成了系統耦合自由度的準線性頻率響應函數矩陣。將它們代入到式（15）中，即可求得非線性子結構在不同響應幅值下的準線性頻率響應函數。以點為例，其驅動點頻率響應函數的求解結果見圖9。對該頻率響應函數進行參數識別，并擬合模態參數與響應幅值的關系。

圖9 a點的驅動點頻率響應函數在不同響應幅值下的解耦結果

只要給定激勵的幅值，即可代入式（18）進行求解。為驗證求解結果，使用ABAQUS顯式動力學模塊對激勵為1 N時若干頻率點的響應進行計算，并將計算值與預測值進行對比，結果見圖10，兩者保持高度一致。

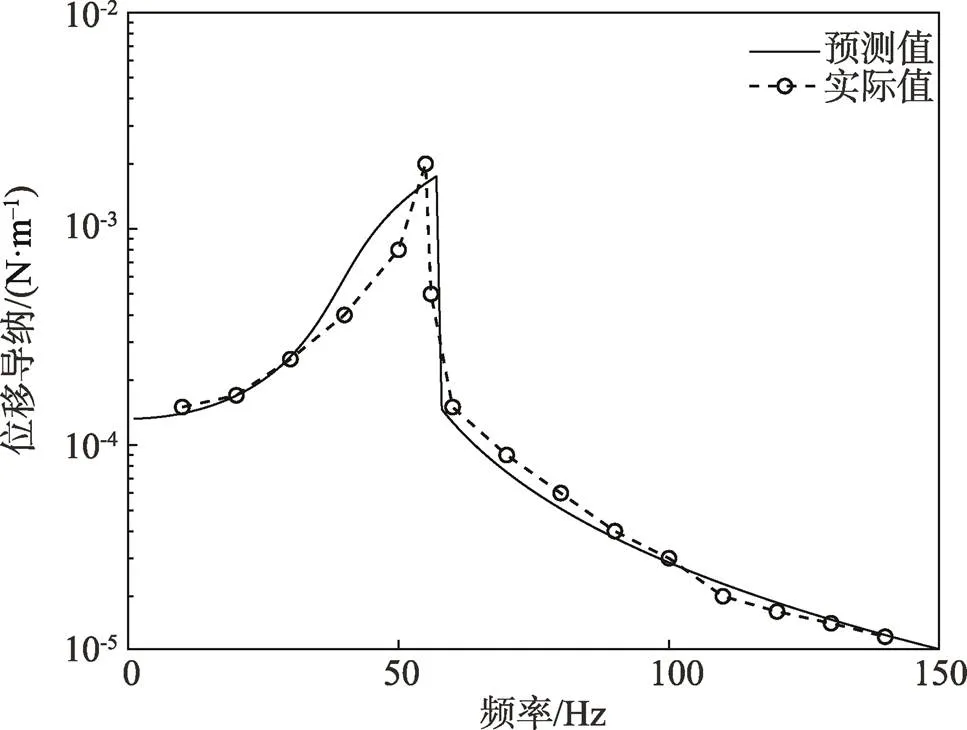
圖10 在a點進行掃頻激勵的頻率響應函數預測值實際值對比

3 結語

考慮到包裝結構和包裝材料的非線性與運輸包裝系統耦合形式的復雜性，文中提出了一種針對非線性多點耦合系統的解耦方法，能夠在不拆解系統的前提下，通過測量運輸包裝系統的頻率響應函數來求解包裝件的動態響應特性，具體步驟如下。

1）使用激振器對系統施加簡諧激勵，測量系統耦合位置在不同響應幅值下的準線性頻率響應函數。

2）使用逆向子結構方法求解非線性子結構在不同響應幅值下的準線性頻率響應函數。

3）識別非線性子結構的模態參數并擬合其模態參數與響應幅值之間的關系。

4）構建激勵幅值與響應幅值之間的關系方程并進行求解。

在集總參數模型和有限元連續模型中，文中方法對非線性子結構振動響應特性的預測結果與實際值基本吻合，證明了其有效性，在運輸包裝系統參數獲取與模型構建、運輸過程產品狀態監測等方面具備應用前景。

[1] WANG zhi‐wei, ZHONG lin‐lin. Finite Element Analysis and Experimental Investigation of Beer Bottle‐Turnover Boxes Transport Unit under Random Vibration Excitation[J]. Packaging Technology and Science, 2020, 33(6): 197-214.

[2] 高德, 吳朝武, 陸俊杰. 運輸包裝系統振動行為研究與發展趨勢分析[J]. 包裝工程, 2020, 41(15): 51-58.

GAO De, WU Chao-wu, LU Jun-jie. Dynamic Behavior Research and Dynamic Development of Transportation Packaging System[J]. Packaging Engineering, 2020, 41(15): 51-58.

[3] WANG Zhi-wei, ZHANG Yuan-biao. Dynamic Characteristic Analysis of Refrigerator-Truck Transport System by Using Inverse Substructure Method[J]. Packaging Technology and Science, 2014, 27(11): 883-900.

[4] ZHANG Yuan-biao, WANG Zhi-wei. Investigation of Frequency Response Function of Product-Transport System Based on Multi-Coordinate Coupled Inverse Substructure Method[J]. Packaging Technology and Science, 2014, 27(5): 364-375.

[5] WANG Jun, SUN Guo-hua, LU Li-xin, et al. Indirect Inverse Substructuring Theory for Coupling Dynamic Stiffness Identification of Complex Interface between Packaged Product and Vehicle Transport System[J]. Packaging Technology and Science, 2015, 28(2): 141-155.

[6] WANG Jun, WANG Qi-li, LU Li-xin, et al. Inverse Sub-Structuring Theory for Coupled Product Transport System Based on the Dummy Masses Method[J]. Packaging Technology and Science, 2016, 29(3): 189-200.

[7] WANG Jun, HONG Xiang, QIAN Yi, et al. Inverse Sub-Structuring Method for Multi-Coordinate Coupled Product Transport System[J]. Packaging Technology and Science, 2014, 27(5): 385-408.

[8] MENG Tian-ya, WANG Jun, PU Guang-yi, et al. Inverse Sub-Structuring Method for Multi-Coordinate Rigidly Coupled Product Transport System Based on a Novel Shearing Probe Technique[J]. Packaging Technology and Science, 2017, 30(9): 601-618.

[9] WANG Jun, WANG Zhi-wei, LU Li-xin. Step-by-Step Decoupling Method for Inverse Substructuring Analysis of a Three-Component Coupled Packaging System[J]. Journal of Vibration and Control, 2015, 21(4): 676-683.

[10] 傅苗苗, 王軍, 盧立新, 等. 多重門限奇異值分解方法的實例驗證[J]. 包裝工程, 2021, 42(21): 176-180.

FU Miao-miao, WANG Jun, LU Li-xin, et al. Example Verification of Multi-Threshold Singular Value Decomposition Method[J]. Packaging Engineering, 2021, 42(21): 176-180.

[11] 傅苗苗, 王軍, 盧立新, 等. 基于頻率響應函數的逆子結構方法誤差分析[J]. 包裝工程, 2021, 42(23): 141-145

FU Miao-miao, WANG Jun, LU Li-xin, et al. Error Analysis of the Inverse-Substructuring Method Based on Frequency Response Function[J]. Packaging Engineering, 2021, 42(23): 141-145

[12] JOODAKY A, BATT G S, GIBERT J M. Prediction of Cushion Curves of Polymer Foams Using a Nonlinear Distributed Parameter Model[J]. Packaging Technology and Science, 2020, 33(1): 3-14.

[13] YANG Song-ping, WANG Zhi-wei. Acceleration Spectrum Analysis of Hyperbolic Tangent Package under Random Excitation[J]. Packaging Technology and Science, 2021, 34(9): 579-587.

[14] 應玉萍, 王花蘭. 基于幾何非線性的果蔬運輸隔振系統設計[J]. 包裝工程, 2020, 41(19): 153-158.

YING Yu-ping, WANG Hua-lan. Design of Vibration Isolation System for Fruit and Vegetable Transportation Based on Geometric Nonlinearity[J]. Packaging Engineering, 2020, 41(19): 153-158.

[15] WANG Peng-tao, WANG Jun, LIM T C, et al. A Strategy for Decoupling of Nonlinear Systems Using the Inverse Sub-Structuring Method and the Parametric Modal Identification Technique[J]. Mechanical Systems and Signal Processing, 2020, 140: 106695.

[16] KARAA?A?L? T, OZGUVEN H N. Experimental Modal Analysis of Nonlinear Systems by Using Response-Controlled Stepped-Sine Testing[J]. Mechanical Systems and Signal Processing, 2021, 146: 107023.

A Decoupling Method for Multi-coordinate Coupled Transport Packaging System Containing Nonlinear Sub-structure

WANG Wei-kai1,WANG Jun1,LU Li-xin1,PAN Liao1,HOU Xue2

(1. Jiangnan University, Wuxi 214122, China; 2. Wuxi Branch of Shantou Dongfeng Printing Co., Ltd., Wuxi 214000, China)

The work aims to optimize the traditional inverse sub-structuring method, to get the dynamic response characteristic of sub-structure in nonlinear multi-coordinate coupled system, which is helpful to resolve the issue that complex coupling forms and nonlinear characteristic of material make it difficult to measure the physical parameters in transport packaging system. The description function method is used to linearize the nonlinear system and the frequency response functions (FRFs) at several response amplitudes need to be measured. Then, the modal parameters of the sub-structure can be identified by inverse sub-structuring method. Lastly, the relationship between the modal parameters and vibration amplitudes is fitted and a function is constructed to describe the dynamic response characteristic of the sub-structure. In the lumped parameter model, the predicted response was consistent with the actual. In the finite element model, the prediction error of the response peak was less than 5%, and the prediction error of the jumping frequency was less than 3%. The application of traditional inverse sub-structuring method was extended to nonlinear multi-coordinate coupled system, which had guiding significance for the construction of dynamic model of complex transport packaging system and the design of anti-vibration packaging.

inverse sub-structuring method; transport packaging; vibration; nonlinear

TB485.3

A

1001-3563(2022)23-0252-07

10.19554/j.cnki.1001-3563.2022.23.030

2022?02?28

國家一流學科建設輕工技術與工程（LITE 2018–29）

王維凱（1997—），男，碩士生，主攻運輸包裝。

王軍（1982—），男，博士，教授，主要研究方向為運輸包裝、包裝新材料。

責任編輯：曾鈺嬋