掌握基本解題策略 提高數學運算能力

福建省龍巖市高級中學 (364000) 謝盛富

1 引言

數學運算是課程學習情境的范疇，是數學學科核心素養之一，在高中數學占有重要地位，運算求解能力是五個“關鍵能力”之一.《課程標準》明確指出，數學運算是依據運算法則解決數學問題的素養，主要包括理解運算對象、掌握運算法則、探究運算思路、選擇運算方法、設計運算程序、求得運算結果等，是解決數學問題的基本手段.在學習中發展數學運算能力，優化解題策略，提高解題效率，借助運算方法解決問題，通過數學運算促進思維發展，倍受關注.

2 基本解題策略

2.1 勤思少算，優化數學運算過程

在教學中應緊扣教材、立足學情，注重基礎，充分發揮例習題的功能，通過知識與方法的遷移，提升思維的廣度和深度，勤于思考，減少計算量，優化運算過程，提升學科素養.“設而不求”是一種化歸與轉化的思想策略，能有效地化復雜為簡單，化抽象為直觀，以此舉例說明.

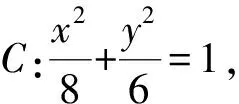
解析：由題意知直線l的斜率k存在，由點斜式設直線l的方程，再聯立橢圓C的方程，消y整理得到關于x的一元二次方程，利用韋達定理結合中點坐標，可求直線l的斜率.聯立方程組是處理直線與圓錐曲線位置關系問題的通性通法，但是計算量偏大，是否有更簡潔的求解方法呢？

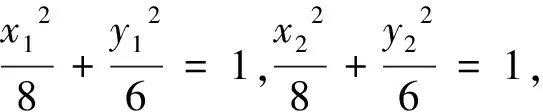
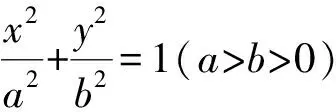
2.2 特值驗證，減少數學運算過程

利用特殊情況代入驗證、排查是解客觀題的重要手段，也常見于解答題中，往往有事半功倍之效.

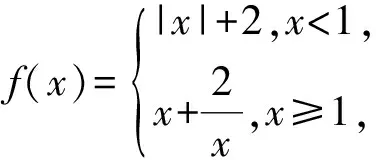
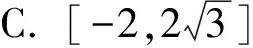
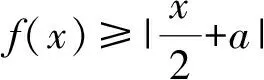
2.3 近似估算，簡化數學運算過程

近似估算法在解題中也是常見方法，在不需要精確的情況下，采用近似估算法能把問題簡單化，簡化數學運算過程，迅速確定答案.

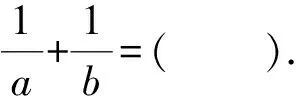
A.-1 B.lg7 C.1 D.log710

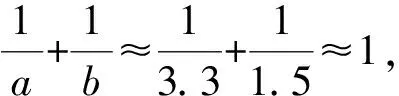
此外，近似估算也常用于多個數的比較大小中，比較大小時往往不需要知道具體數值，只要借助單調性比較它們的大小，或者估算出它們大致所在范圍，如大于1，還是介于0到1，或者小于0，或者其它中間量.

2.4 逼近思想，美化數學運算過程

逼近思想，是指變量趨近于某個數值時，另一變量因此趨近于另一個數值.其中，極端思想是逼近思想的簡化版.在求取值范圍或判斷函數的大致圖象時，結合逼近思想能準確迅速求解問題.逼近思想有時也應用在導數解答題中.

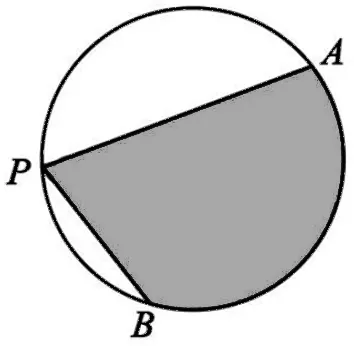
圖1

例4 (2019年高考北京卷文科第8題)如圖1，A，B是半徑為2的圓周上的定點，P為圓周上的動點，∠APB是銳角，大小為β.圖中陰影區域的面積的最大值為( ).

A.4β+4cosβB.4β+4sinβ

C.2β+2cosβD.2β+2sinβ

解析：利用極端思想，當β→0時，弧長AB無限逼近零，陰影區域的面積趨于零；排除選項A、C；當β→π時，弧長AB無限逼近圓周，陰影區域的面積趨于π×22=4π；排除選項D.選B.

2.5 平幾知識，巧妙求解簡化運算

平面幾何知識豐富、優美，比如平行與相似、中位線、中垂線、等邊三角形、三角形的“四心”與內角和、角平分線、圓直徑所對圓周角是直角、直角三角形中斜邊上的中線等于斜邊的一半等.如果能夠充分利用平幾知識，不忘特殊與轉化，巧妙地優化解題過程，簡化其中的運算，尤其常見于求解圓錐曲線問題，往往達到事半功倍之效.

例5 (2021年新高考全國Ⅰ卷第14題)已知O為坐標原點，拋物線C：y2=2px(p>0)的焦點為F，P為C上一點，PF與x軸垂直，Q為x軸上一點，且PQ⊥OP.若|FQ|=6，則C的準線方程為.

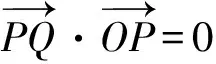
2.6 回歸定義，突出本源運算便捷

定義是數學知識的本源，有了定義才會枝繁葉茂，沒有定義則是無源之木.比如，對雙曲線下定義后，根據定義，建系列出等式，化簡得到雙曲線的方程，再研究幾何性質.因此在平時解題中應積極回歸定義，注意數形結合，在解題運算過程中體現更便捷，喜獲答案.

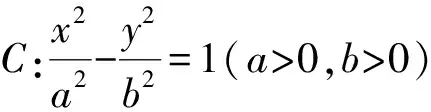
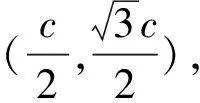
2.7 一題多解，鍛煉數學運算能力

一題多解是從多角度研究問題和認識試題背景，它可以發散學生思維，破解思維定勢的局限，訓練學生不同的解題能力，不但能有效整合各知識板塊的思想與方法，而且能有效鍛煉數學運算能力.

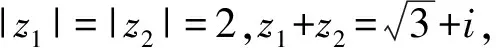
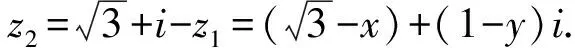
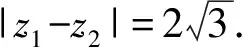
圖2

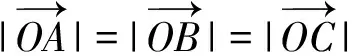
此外2021年全國高考甲卷理科第15題、文科第16題也有上述解法的影子，至少可從四個角度去分析與求解，有興趣的讀者可以嘗試解答.

2.8 多題一解，培養數學運算思維

多題一解能實現減負增效，掌握解決數學問題的本質，促進對數學解題的深度理解，培養數學運算思維，感受知識與方法的內在聯系，把數學核心素養的培育融合于課內外.

題1 設拋物線C：y2=4x的焦點為F，直線l過F且與C交于A，B兩點.若|AF|=3|BF|，則l的方程為.

題2 已知直線y=k(x+2)(k>0)與拋物線C：y2=8x相交于A，B兩點，F為C的焦點，若|FA|=2|FB|，則k=.

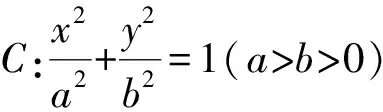
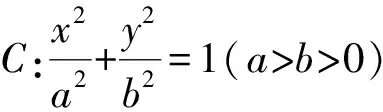
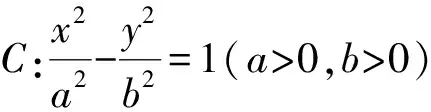
上述每道題各自可從多角度求解，但也有相同解法，對培養學生的數學運算思維有很大的幫助.在教學中以題1作為例題引入，完成分析、講解與剖析之后，給出了題2和題3作為課堂練習，題4和題5作為課后作業完成，旨在從直線過焦點到不過焦點、從拋物線到橢圓、雙曲線，一次次的體驗與感悟，激發學生的探究興趣，培養分析問題、解決問題、探究能力和數學運算能力.

3 總結

在立德樹人的背景下，現今高考試題命制在不斷地反套路、反刷題，考查的重點依舊是思維品質和核心素養.在教學中，教師可根據教學需要，結合學情，創設真實又合適的問題情境，滲透數學思想與方法，點撥解題的各種策略與對應的視角，積極培養數學思維，在鞏固已有的通性通法的基礎上，適當掌握一些簡單又易于掌握的解題技巧，在特殊技巧上錦上添花，獲得更多的真實體驗、知識方法與成績的收獲，讓巧妙方法成為解題的通性通法，從中提升數學運算的運用策略，提高數學運算能力，春風細雨潤物無聲，不斷總結、反思，悟出運算之妙！