利用極坐標(biāo)簡(jiǎn)解兩道期末解幾試題

重慶實(shí)驗(yàn)外國(guó)語學(xué)校 (400039) 李小燕

極坐標(biāo)與直角坐標(biāo)相比，極坐標(biāo)以極徑與夾角為基本參數(shù).在解決解析幾何相關(guān)問題時(shí)，會(huì)更加便捷.本文以兩道解析幾何試題，探討如何利用極坐標(biāo)的思想進(jìn)行求解.

一、試題展示

題1 (2021-2022學(xué)年上學(xué)期佛山市高二質(zhì)量檢測(cè)，16)已知圓C:(x-4)2+(y-2)2=4和點(diǎn)M(4,4)，若點(diǎn)N為圓C上一動(dòng)點(diǎn)，點(diǎn)Q為平面上一點(diǎn)且∠MQN=90°，求點(diǎn)Q縱坐標(biāo)的最大值.

綜上可知，上述兩個(gè)問題均可轉(zhuǎn)化為相關(guān)邊長(zhǎng)的范圍.結(jié)合極坐標(biāo)的特點(diǎn)，只要設(shè)計(jì)恰當(dāng)?shù)貥O坐標(biāo)，即可高效的解決上述兩個(gè)問題.

二、解法呈現(xiàn)

圖1

關(guān)于題1，如圖1，根據(jù)圓的垂徑定理，可得CP⊥MN，從而可得點(diǎn)點(diǎn)P的軌跡是以CM為直徑的圓P:(x-4)2+(y-3)2=1.

根據(jù)上述分析可知點(diǎn)Q縱坐標(biāo)的最大值為yP+PM.為了方便計(jì)算，可構(gòu)造一個(gè)新的圖形對(duì)該問題進(jìn)行轉(zhuǎn)述.如圖2，設(shè)點(diǎn)P的軌跡為K:x2+(y-1)2=1，以及直線l:y=4.試計(jì)算OP+dP-l的最大值.

圖2

圖3

反思：利用極坐標(biāo)進(jìn)行求解，直擊問題的本質(zhì)，運(yùn)算量低，且便于推廣.當(dāng)將直線l進(jìn)行平行移動(dòng)時(shí)，僅需將最終的最值進(jìn)行相應(yīng)的平移即可.

圖4

綜上可知△OPQ的邊PQ上的高為定值.

三、一般化結(jié)論

上述解法可將該結(jié)論推廣至一般性的橢圓.

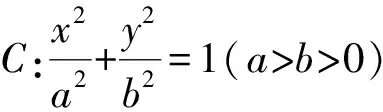
類比橢圓，也可將該結(jié)論推廣至雙曲線與拋物線.