例析外接球問題求解的三種模型

江西省萍鄉市教學研究室 (337000) 胡 斌

基金項目：江西省教育科學“十四五”規劃2021年度普通類重點課題——高中數學直觀想象核心素養提升的實踐研究(21PTZD022)

幾何體外接球問題是立體幾何中非常有趣且培養直觀想象素養的一類經典問題，此類問題實質是解決球的半徑長或確定球心的位置問題，其中球心的確定是關鍵.解決與球有關的問題對直觀想象核心素養有較高的要求，在求解此類問題時，很多學生往往不得要領.教學中常用的方法是針對不同幾何體的特性進行歸類總結為如補形法、墻角模型法、向量法等，類型多，但普適性不強.本文通過利用球內相關量的幾何關系，挖掘不同幾何體的共性，從給定的前提和條件出發，總結出求解立體幾何中外接球問題(主要是求外接球的半徑R)的三種模型.

模型一 幾何體中存在某一條側棱(或母線)垂直底面

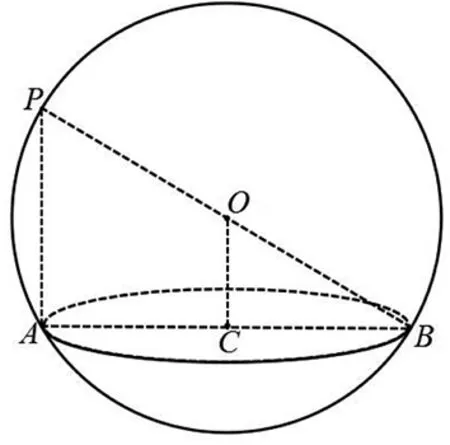
圖1

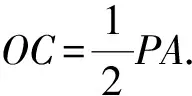
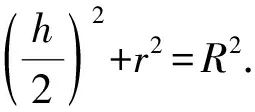
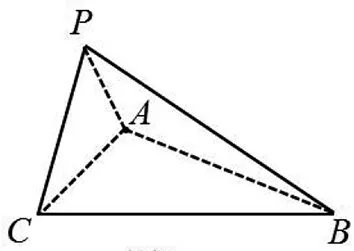
圖2

例1 如圖2，在三棱錐P-ABC中，平面PAC⊥平面ABC，AB⊥AC，PA=PC=AC=2，AB=4，則三棱錐P-ABC的外接球的表面積為( ).

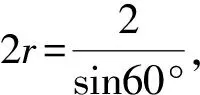
評注：模型一的關鍵在于需要有線面垂直，利用“外接球球心與底面外接圓圓心的連線垂直于底面”這一結論，適用面廣，條件易滿足，只要有線面垂直即可適用，也可如例1這樣，把圖形調整后滿足模型一的條件，從本質上構建出數學問題的直觀模型，需注意，此處的“線”需為側棱或母線.

模型二 幾何體中存在某一條側棱(或母線)滿足其頂點在底面的投影位于底面外心

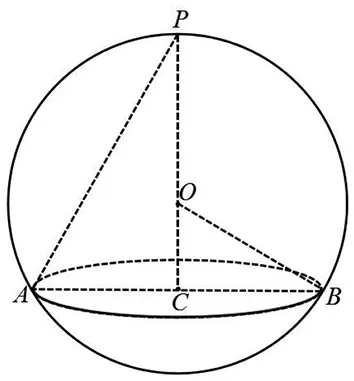
圖3

背景：如圖3，某幾何體的外接球為球O，半徑為R，底面的外接圓為截面圓C，半徑為r，其側棱(或母線)PA(A為底面頂點或底面圓周上一點)滿足：頂點P在底面的投影為圓心C，則易知球心O在PC上，且OC=PC-R.

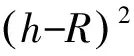
例2 如圖4(1)，已知平面四邊形ABCD滿足AB=AD=2，∠A=60°，∠C=90°，將△ABD沿對角線BD翻折，使平面ABD⊥平面CBD，如圖4(2)，則四面體ABCD的外接球體積為.

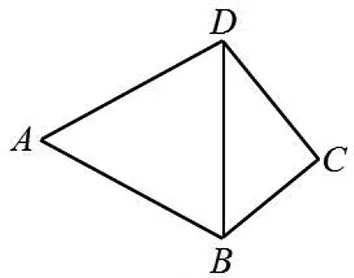
(1)

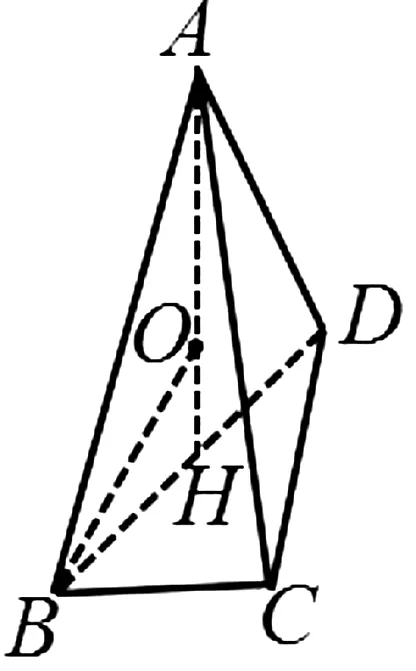
(2)

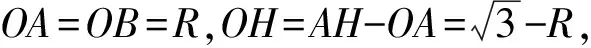
評注：模型二的關鍵在于需要有三點一線(側棱端點、球心、圓心)，通過多面體的一條側棱或旋轉體的一條母線和球心或接點作出截面圖，把空間問題化歸為平面問題.摒棄復雜圖形的分析過程，借助幾何直觀和空間想象感知事物的形態，剖析問題本質.

模型三 幾何體中任意一條側棱(或母線)既不垂直底面，其頂點在底面的投影也不位于底面外心

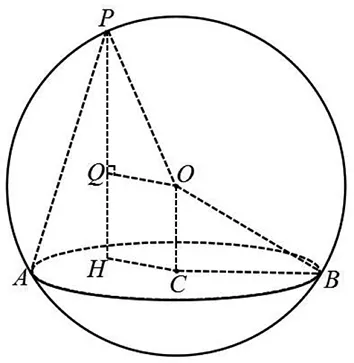
圖5

背景：如圖5，某幾何體的外接球為球O，半徑為R，底面的外接圓為截面圓C，半徑為r，其任意一條側棱(或母線)(不妨取為PA，A為底面頂點或底面圓周上一點)滿足：PA與⊙C不垂直，且頂點P在底面的投影H與圓心C不重合(H與C的距離CH叫做偏心距)，過O作OQ⊥PH，垂足為Q.則易知OC∥PH，OQ∥CH；設PQ=x，則OC=QH=PH-x.

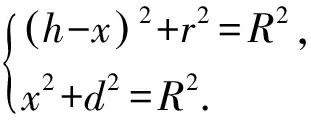
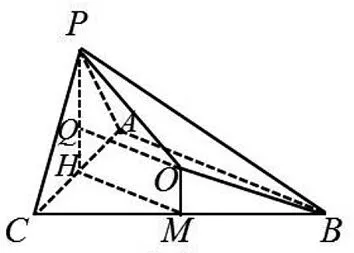
圖6

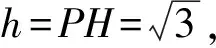
評注：模型三不像模型一和模型二那樣具有條件的限制，任何一個立體圖形，只要能找到高和偏心距，即可構建關于外接球半徑的方程組，從而求出立體圖形的外接球半徑.其核心思維主要是利用球心的性質，搭建兩個直角三角形為橋梁，不失一般性，本模型可解決前兩個模型之外的無特殊條件的大部分幾何體的外接球問題.

關于外接球問題，根據立體圖形的不同特征有很多成熟的結論.本文站在探尋本質，尋求直觀的立場上，嘗試從另一個角度出發，抓住一個條件的改變導致立體圖形的本質變化，從而建立起從特殊到一般的模型系，進一步構建數學問題的直觀模型，建立形與數的聯系，借助空間認識事物，從而加深學生對數學問題的理解，有助于剖析問題的本質特征，充分體現了高中數學直觀想象核心素養的優勢和可提升的實踐依據.