展開數學說理 訓練邏輯思維
——以《長方體與正方體》教學為例
林斌
(平潭北厝鎮中心小學,福建 平潭 350400)
數學說理作為一種新型教學策略,重在引導學生在內化知識的前提下,能夠以數學理論為依據,通過嚴謹的數學表達來剖析、梳理問題情景中的數理關系,講明數學中的道理,深化學習層次。在小學階段,教師注重培養學生的說理能力,既能引導其體會數學的理性魅力,深化知識理解;又能訓練其邏輯思維、辯證素養與抽象能力,教學效益足。[1]對此,文章聚焦五年級下冊《長方體與正方體》教學,對如何有效開展數學說理活動,提升學生思維的研究展開探究。
一、小學數學說理教學存在的問題
(一)教學問題設置不夠深入
在教學中,由于很多教師對數學說理的理解不夠深入,加之其教學理念尚未完全更新轉化,仍以趕教學進度為主導致不少教師在說理教學中往往多注重形式而忽視所設計的問題是否能達到啟智增慧,有效提升學生的思維等目標,導致問題設置的深度性不夠。
(二)說理題目難度缺乏針對性
在教學中,每位學生都是獨特的,其思維邏輯、認知特點、學習基礎等必然存在著一定的差異性。但很多教師囿于以往的教學習慣,傾向于讓全體學生針對統一化的、與其學習水平不適配的問題展開思考與說理,造成教學效果不盡如人意。
二、小學數學說理教學的策略
(一)創建觀察過程,引導有序說理
數學說理作為一種教學手段,其最終的指向在于“啟智增慧”。對此,在小學數學課堂中,為深化學生對基礎知識的理解、鍛煉他們數學表達的條理性與邏輯性,教師可以結合學科知識特點,為學生創建一些觀察過程,引導他們根據已學概念與性質,對圖像進行判斷、說理。使其在有序的表達中不斷深化自身思維、明確數理關系、提升數學素養,以達到“將知識內化于心、將思維過程外化于行”的啟智目標。
例如在人教版五年級下冊《長方體與正方體》中,當學生已經理解“長方體”相關的概念及性質后,為深化他們對知識的掌握,鍛煉其有序表達的能力,教師出示了下述圖形引導學生觀察,點撥其在辯理、說理中明晰概念內涵、提升邏輯表達素養。[2]具體如下題所示:
判斷下列哪些是長方體?說說你的依據什么。

從問題設置來看,該說理題目以“易混淆”的圖形來鍛煉學生運用概念進行判斷與表達的能力。在實際說理中,大部分學生均能輕易判斷出1、4 為長方體,3、5 不是。但圖2 卻難以一眼看出,因為其棱長和面數量的均符合長方體的性質。這時就需要學生細致觀察與分析才能作出正確選擇。于是有學生發現在面形狀上,圖2 有4 個梯形不符合“長方體6 面全為長方形”的特征。故排除該選項。事實上這種集觀察、分析與說理為一體的教學方式,能夠很好地強化學生的數學理解、空間觀念及條清縷析的邏輯表達。
(二)設計分層問題,培養說理能力
在以“生本理念”為中心的小學數學課堂中,為了讓“數學說理”的教學發揮最大的功效,促使大多數學生能從中獲益,教師還應考慮不同層次的學生在學習需求、學業能力及心理特點上的差異性,為其精心設計梯度分明、合理有度的說理題目,來訓練學生運用知識展開邏輯分析的能力,促使他們在“各就其位”“各居其層次”的說理活動中,不斷夯實自身的基礎、提升自身的剖析問題能力、數學表達素養和抽象邏輯思維。
例如,在日常教學中,為讓各層次的學生均能參與說理活動,培養其說理意識、數學表達與學習信心,教師會根據學生的學情,有針對性地為他們設置一些難度有別、梯度分明、實效性高的題目,引導他們進行說理。具體題目為表1 所示:
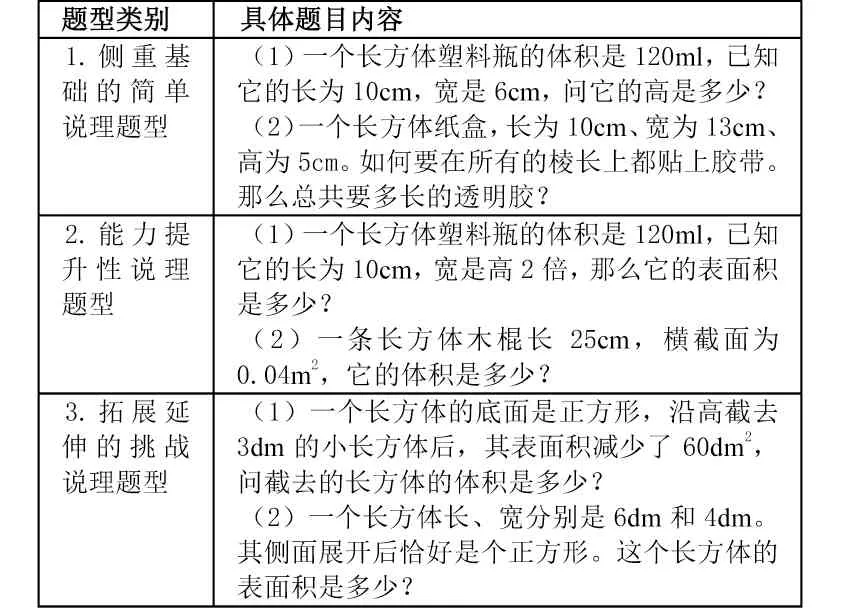
表1
在教學實際中,簡單類的題型主要由后進生來完成,旨在引導他們在說理中能夠不斷鞏固基礎、提升自信、增強表達的條理性;能力提升類主要由中等生與先進生完成,鼓勵他們在找到解題切入點的前提下,能疏通思路進行條清縷析地說理,以提升其邏輯表達素養與理性精神;挑戰類說理主要由先進生參與,中等生根據自身能力選擇性參與。事實上這種梯度分明、難易有別的分層說理,能夠引導學生感受數學知識的理趣與智趣氛圍,提升其說理興趣與邏輯思維。
(三)巧設問題陷阱,提升辨析素養
思維具有內隱性,往往需要語言將其外顯化。在小學階段,教師鼓勵學生進行說理,正是引導學生將“自身的數學思維與知識吸收程度顯性化”的有效手段。對此,數學說理課堂中,為切實提升學生對知識融會貫通的能力、有效拓寬其思維,增強其思辨力,教師可以“知識點”為核心,巧妙設計一些學生易錯的、看似有理有據實則錯誤的問題陷阱,來引導學生進行辨析說理。促使他們在兼具“智趣與理趣”氛圍中,不斷深化自身的邏輯思考素養與理解力。
例如,當學生掌握“正方體”的知識點后,為深化其對該知識的理解,教師便采用數理推導的方法,引導他們展開說理論證。教師先在幾何畫板中任意畫一個正方體,點撥學生思考如果它的棱長擴大3 倍,那么其棱長總和擴大多少?對此,大多數學生能根據公式L原=12a 得出擴大后:L擴=12×3a,進而得出總周長擴大3 倍的結論。隨后,教師便在教學白板中出示問題陷阱“正方體的棱長擴大3 倍,其體積是否也都擴大3 倍?”這時有不少學生根據直覺紛紛陷入了陷阱中,不假思索地就贊成這一論述。也有部分學生實事求是,結合自身的計算與推演對這一論斷提出質疑,表示:棱長擴大3 倍,變化后體積V擴=(3a)3=27V原,即是原來的27 倍……以此,直擊學生思維盲點的數學陷阱引導他們學會質疑,懂得利用已學知識進行分析,有力反駁錯誤論述。既提升了學生思維的層次性與邏輯力,又幫助他們透徹理解知識。
三、結語
數學說理能力與思維的提升是一個循序漸進的過程,在教學實際中,教師應當圍繞知識核心、立足實際,聚焦學生思維誤區來設計高質量的數學問題[3],引導學生在理趣、智趣的生態啟智增慧,不斷強化剖析問題和邏輯表達的能力,提升質疑精神與學科素養。

