基于類比推理的高中數(shù)學解題教學思考

【摘要】為了能夠更好地培養(yǎng)高中生的數(shù)學思維，加強數(shù)學課堂中的解題指導是重要的途徑之一.隨著我國教育改革的不斷深入，高中數(shù)學課程中的題目具有更加明確的考查目標，對于學生數(shù)學思維有著直觀反映.類比推理是重要的數(shù)學思維之一，也是高中學生必備的解題方法.高中數(shù)學教師為學生基于類比推理進行數(shù)學解題教學，對學生的數(shù)學解題思維培養(yǎng)起到了極大的推動作用.本文基于類比推理進行分析，得出利用類比推理進行解題的策略.

【關鍵詞】類比推理;高中數(shù)學;解題教學

在高中階段的數(shù)學教學中，不僅應當為學生教授課本上的理論知識，還應當培養(yǎng)學生的解題思維，只有學生掌握了數(shù)學的解題思維，學生在數(shù)學考試時才能夠充分地利用課堂上學習到的理論知識進行解題，形成自己的解題思路，這樣有助于解題效率的提升，對學生的數(shù)學成績提升具有十分重要的作用.因此在高中數(shù)學的教學過程當中，應當不斷地培養(yǎng)學生的數(shù)學解題思維，利用類比推理教學，對學生的數(shù)學解題思維培養(yǎng)有著促進作用，能啟發(fā)學生的解題思維，幫助學生開拓解題的思路.所以在高中數(shù)學教師為學生進行基礎理論知識講解的同時，應當注重培養(yǎng)學生的數(shù)學解題思維，使得學生的綜合素養(yǎng)得到有效的提升.

1 類比推理內(nèi)涵

隨著我國的教育改革不斷地向前推動發(fā)展，類比推理在高中數(shù)學的解題過程中發(fā)揮著越來越重要的作用.因此，了解類比推理的內(nèi)涵，分析類比推理運用的現(xiàn)狀十分有利于學生的數(shù)學學習，使他們的數(shù)學成績能夠得到有效的提升.類比推理是指在數(shù)學的教學以及學習活動當中，教師利用相同的問題，從多個角度為學生進行講解，使得學生能夠從多方面的角度進行問題的解答，同時能夠發(fā)散學生的思維，有利于學生數(shù)學解題思維的形成，對學生未來獨立自主解決數(shù)學問題有著極其重要的作用.通過類比推理教學的開展，可以使得學生在進行數(shù)學問題解答時，更加具有邏輯條理性，并且以邏輯思維為核心，從多方面進行數(shù)學問題解答，這樣的數(shù)學答案能夠更加全面，這對學生數(shù)學成績的提升具有十分重要的作用.

通過對學生進行類比推理教學，使得學生的思維能力得到有效的提升，有利于學生在數(shù)學問題解答的過程當中，能夠在短時間內(nèi)了解問題當中蘊含的數(shù)學含義.提升了學生的數(shù)學解題效率，同時這樣的教學方法適用于當下的現(xiàn)代化教學，能夠培養(yǎng)出符合當今時代所需求的人才.此外對學生進行類比推理教學，能夠激發(fā)學生的數(shù)學學習興趣，使得他們能夠積極主動地進行數(shù)學學習.激發(fā)學生的求知欲和探索欲，對學生的學習成績提升具有十分重要的作用.為此高中數(shù)學教師應當充分理解類比推理的教學內(nèi)涵，便于為學生進行類比推理方法的教學活動.高中數(shù)學教師在對學生的教學時，應當充分的理解類比推理教學思想的內(nèi)涵，這樣才能夠更好地為我國培養(yǎng)出優(yōu)秀的數(shù)學人才.

2 高中數(shù)學解題類比推理應用價值

類比推理在高中數(shù)學解題教學當中占據(jù)著十分重要的作用.通過類比思想，首先可以實現(xiàn)數(shù)學當中的新舊知識之間的連接.因為數(shù)學知識存在著一定的邏輯關系，因此在學生進行新知識內(nèi)容學習時，可以以舊知識內(nèi)容為基礎，通過類比推理為連接點，便于學生理解接受新知識，使得學生的學習效率得到有效的提升，這對學生綜合素養(yǎng)的形成具有十分重要的作用.但是在目前的教育過程當中，部分數(shù)學教師往往忽略這一點，無法使得學生將新舊知識進行連接，導致了學生不能靈活運用舊知識進行新知識的學習，影響了學生的數(shù)學成績.通過進行類比智力的教學，能夠幫助學生鞏固加深以往的舊知識，并且便于學生理解新的知識，例如在進行等比數(shù)列的學習時，可以從等差數(shù)列的定義以及公式當中找到相同點，這樣能夠幫助學生進行學習.

高中數(shù)學教師在高中數(shù)學的教學過程當中，通過類比推理教學還有助于學生知識體系的形成，因為高中數(shù)學知識較為分散的同時也具有一定的難度，因此學生在進行學習時，往往是分模塊進行數(shù)學知識學習，這樣容易造成數(shù)學知識體系凌亂，不利于學生后期的深度學習.因此教師通過類比推理教學，推動學生知識體系的形成，有助于學生了解數(shù)學當中的規(guī)律，使得他們在進行數(shù)學學習時，能夠有效地提升他們的學習效率.此外還可以深化學生對數(shù)學知識的認知，改變了以往數(shù)學在學生眼中單一枯燥性的固有認知.因此在對高中數(shù)學進行講解時進行類比推理教學具有十分重要的意義.

3 提升類比推理在高中數(shù)學解題中的應用策略

3.1 利用類比推理，創(chuàng)新教師教學理念

在我國教育改革不斷發(fā)展的背景之下，為了能夠更好地為學生進行高中數(shù)學的教學，應當首先改變并且創(chuàng)新教師的教學理念，只有這樣才能夠更好地培養(yǎng)出適應當下社會需求的數(shù)學人才.如果教師在高中數(shù)學的教學過程當中，一味地利用固有的教學方法為學生教學，很難吸引學生的學習興趣，反而會造成學生對數(shù)學學習的排斥.因此高中數(shù)學教師應當不斷創(chuàng)新他們的教學方法，利用新型的教學手段吸引學生的學習興趣，使得高中生們能夠獨立自主地進行高中數(shù)學學習.類比推理教學，在高中數(shù)學的教學過程當中占據(jù)著重要的作用，它能夠培養(yǎng)學生形成數(shù)學解題的邏輯性思維，對學生的數(shù)學學習有著十分重要的作用.因此高中數(shù)學教師可以利用類比推理的教學方法，創(chuàng)新他們的教學理念，使其能夠更好地為學生提供優(yōu)質(zhì)的教學資源，這樣才能夠不斷地培養(yǎng)學生的數(shù)學解題邏輯性思維，有利于學生數(shù)學成績的有效提升.

利用類比推理方法創(chuàng)新，教師的教學理念是應當基于教學大綱進行創(chuàng)新，不能盲目地進行創(chuàng)新，沿著教學大綱主線進行合理有效的創(chuàng)新，這樣才能夠更好地為學生進行高中數(shù)學教學.通過教師理解并研究類比推理的內(nèi)涵，可以使得教師認識到類比推理教學方法在高中數(shù)學教學當中的重要性.例如在高中數(shù)學教師進行正弦函數(shù)與余弦函數(shù)的理論知識教學時，高中數(shù)學教師可以將二者進行對比教學，使學生研究二者的不同以及相同之處，這樣便于學生進行數(shù)學理解，使得學生能夠在短時間內(nèi)學習到豐富的數(shù)學知識.再如在學習不等式部分的時候，不等式的極值問題是典型題目方向.教師通過類比推理讓學生掌握好知識點的多樣化考查類型.

例1 已知有y=x+1x，且x取值均為正數(shù)，問y的最小值是多少.另外求解：（1） x取負數(shù)，則y最大值是多少.（2）若x取值[2，10]區(qū)間內(nèi)，那么y的最大值是多少.（3）若2x+y=5，且x、y均為正數(shù)，問xy的最大值.

解析 在例題1的題目中，高中生可以根據(jù)不等式最值求解的基本要求，直接求解就能得到最小值，即y=x+1x≥2x·1x=2，最小值的條件是x=1x，即x=1時得到最小值.對于類比推理的（1）（2）（3）問題，學生們可以依據(jù)不等式計算的基本條件進行變形后求解.

3.2 利用類比推理，豐富數(shù)學教學方法

因為數(shù)學是高中教學當中的重難點內(nèi)容，因此應當不斷地豐富教學方法，吸引學生的學習興趣，只有使得學生積極主動地進行數(shù)學學習，才能更好地為學生進行數(shù)學教學.在對高中生們進行數(shù)學教學時，應當避免單一地對學生進行灌輸性教學，這樣并不利于學生學習積極性的提升.因此在類比推理教學的背景之下，教師應當不斷地豐富他們的教學內(nèi)容.例如在教學的過程當中應當將數(shù)學中學習過的知識反復復習，并在復習的過程當中摻入新知識內(nèi)容，這樣便于學生利用舊知識理解新知識，能夠使得學生的數(shù)學學習效率得到有效的提升.當下處于信息化時代，因此教師利用信息化手段結合類比推理思想為學生進行教學可以極大地吸引學生的學習興趣.因為目前學生大多熱愛利用手機進行網(wǎng)上沖浪，所以利用信息化手段為學生進行高中數(shù)學教學，可以使得學生更加樂于接受數(shù)學知識的講解.同時還可以在互聯(lián)網(wǎng)當中選取優(yōu)質(zhì)的教學資源，為學生進行數(shù)學教學.

在對學生進行教學時，教師應當鼓勵學生將數(shù)學當中相同的例題進行研究分析，找出他們當中的共同點，這樣可以使得學生在考試過程當中遇到相應的問題時，能夠在短時間內(nèi)理解題目當中所蘊含的數(shù)學知識內(nèi)容，可以有效地提升學生的做題效率.并且結合以往類似的例題進行解答，能夠極大地提升數(shù)學問題的正確率.因此在對學生進行高中數(shù)學的教學過程當中，應當結合當下新興的技術手段，利用類比推理的教學思想，不斷地豐富教師的教學方法，從而使得學生更加熱愛數(shù)學學習.

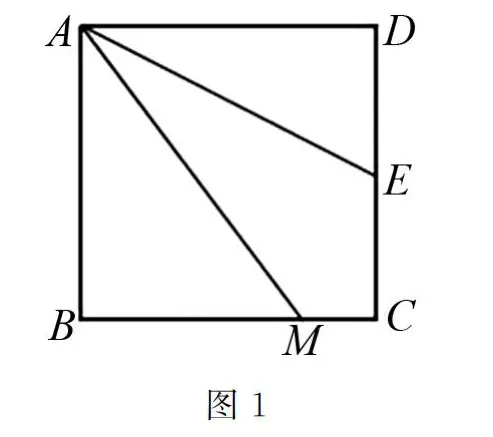
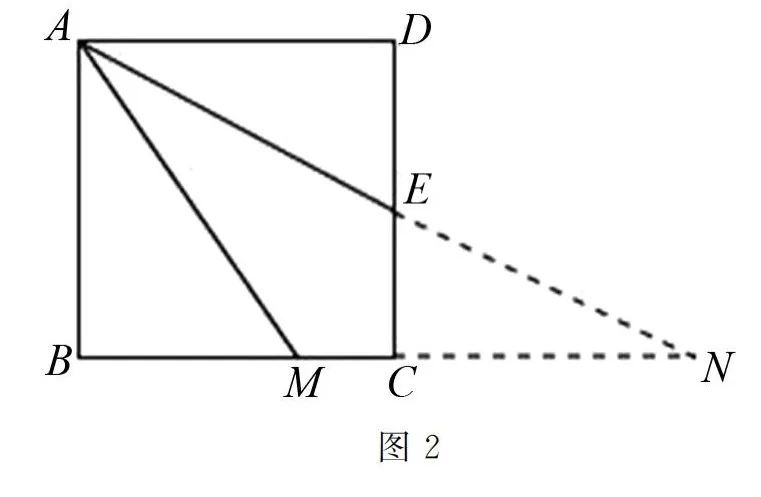
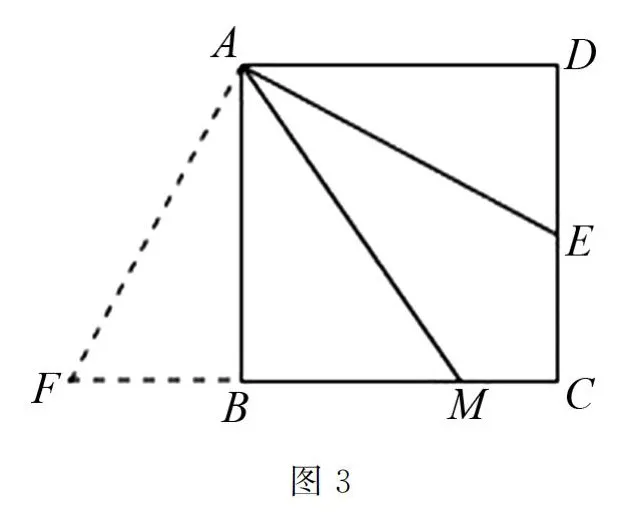
例2 已知有一個正方形ABCD，邊CD的中點為E，在邊BC上有一點M，且線段AE剛好是∠DAM的角平分線.證明：AM=AD+MC，AM=DE+BM是否成立.若ABCD為長寬不相等的矩形，則上述證明結果是否還成立.

解析 對于需要證明的AM=AD+MC、AM=DE+BM這兩個問題來說，在正方形ABCD當中可以進行輔助線考慮.要證明線段的關系，可以構造全等三角形，根據(jù)三角形中公共邊、對應角的條件，將標注出的線段進行等邊轉換，進而證明問題.如圖2構造出MN=MC+CN，只要MN=AM、CN=AD即可，通過△ADE和△NCE的全等來證明.如圖3則關鍵在△ABF和△ADE的全等上.通過類比推理，將矩形ABCD情況下的結論也可以得到驗證.

3.3 利用類比推理，優(yōu)化數(shù)學教學體系

高中教師在利用類比推理教學時，往往會為了類比推理教學而進行類比教學，這樣的想法是錯誤的.在高中數(shù)學教學利用類比推理教學時，應當首先完善數(shù)學教學體系，避免在利用新型的教學模式進行教學時造成本末倒置的情況，防止因為利用新型教育模式教學，使得高中數(shù)學的教學改革產(chǎn)生停滯的局面.因此應當不斷地優(yōu)化數(shù)學教學體系，這就需要學校方面的努力，首先在進行高中數(shù)學教師人才招聘時，應當選取創(chuàng)新理念較強并且接受能力較強的數(shù)學教師，這樣可以使得在為學生教學的過程當中，能夠不斷的創(chuàng)新教學方法，并且容易接受新型的教學模式.可以有效地貫徹落實類比推理思想的教學理念，使得學生能夠接受到更加優(yōu)質(zhì)的教學資源.加強高中數(shù)學的教學體系，使得教學結構不斷的優(yōu)化，更加有利于于類比推理教學的開展.

在優(yōu)化數(shù)學教學體系時，應當首先構建高中數(shù)學教學評價反饋機制.如果教師僅僅在課堂當中為學生進行技術理論知識的講解，而在課下不關注學生的實際學習情況以及生活狀況，這樣會使得教學進程緩慢.因為如果教師不了解學生的實際學習情況，這樣很可能會造成高中數(shù)學教師的教育方法與學生的實際學習情況并不相符，很有可能降低學生的學習興趣.因此應當定期開展教學評價，使得數(shù)學教師了解學生近期的學習情況，然后根據(jù)學生的學習情況制定自身的教學方法，并且對成績優(yōu)異的學生進行鼓勵，使得他們能夠更加自信地進行高中數(shù)學學習.同時也應當對成績欠佳的同學進行鞭策，使這些同學意識到必須努力才能夠獲得更好地成績.也應當構建家校合作機制，讓家長們也參與到高中數(shù)學的教學過程當中，這樣通過家校之間的共同努力，才能夠更好的培養(yǎng)學生的綜合素養(yǎng).

例如 在平面幾何中，三角形任兩邊之和大于第三邊，得出空間相應的結論為三棱錐任意三個面的面積之和大于第4個面的面積.

綜上所述，在對高中生們進行數(shù)學教學時，應當利用類比推理教學理念為學生進行高中數(shù)學教學，使得學生的數(shù)學解題思維得到培養(yǎng)，這樣學生在進行數(shù)學解題時才能夠更具有邏輯思維性，避免在解題時產(chǎn)生迷惑.教師也應當不斷利用類比推理教學理念，創(chuàng)新他們的教學方法，不斷的吸引學生的學習興趣，使得學生能夠更加積極主動地投入到數(shù)學學習過程當中.