鋼筋混凝土柱-鋼梁盒式節點抗剪機理及抗剪承載力計算

劉立平， 肖 閑， 鄭歆耀， 王志軍， 李英民， 李瑞鋒， 鄧 飛

(1. 重慶大學 土木工程學院，重慶 400045； 2. 重慶大學 工程結構抗震防災重慶市重點實驗室，重慶 400045；3. 重慶保利房地產開發有限公司，重慶 401147)

鋼筋混凝土柱-鋼梁(reinforced concrete columns and steel beam，RCS)混合結構綜合了鋼材與混凝土各自的優勢，是一種經濟高效的結構體系。對比鋼結構，鋼筋混凝土柱具有更強的耐久性、耐火性和穩定性；而與鋼筋混凝土結構相比，鋼梁自體質量輕、強度高，提高了空間的利用率，更有利于實現結構的大跨度[1]。對于RCS混合結構，梁柱節點的有效性是保障結構整體性的關鍵。現階段，主要的節點形式有梁貫通型和柱貫通型，國內外學者進行了大量的試驗研究與理論分析。Parra-Montesinos等[2]對9個3/4比例的梁貫通型外部節點進行了低周反復荷載試驗，研究了節點抗彎、抗剪承載力及傳力機理，結果表明RCS節點同樣適用于抗震設防烈度較高的地區，且剛度無明顯削弱。Nishiyama等[3]提出了強柱弱梁作為RCS節點在強地震作用下的設計依據，并建立了12個可應用的柱貫通型梁柱節點模型。傳統RCS節點在性能與施工方面存在一定局限性，許多新型節點從而被提出。Alizadeh等[4]結合有限元模型研究了柱端承板與鋼梁法蘭附加板對于梁貫通型RCS節點位移響應與承載力性能的改良性能。針對梁貫通型節點混凝土澆筑困難的局限性，曹暉等[5]提出新型鋼套箍鋼筋混凝土梁柱節點，避免梁縱筋貫通節點，降低了施工難度。

同時，馬輝等[6-10]對新型RCS混合節點的構造形式、抗震性能和計算方法進行了深入探討，通過試驗得到節點的破壞模式、滯回曲線、位移延性等性能參數并建立了有效的承載力計算公式，對于此類節點的研究具有一定的參考價值。在汲取和消化了國內外學者相關研究的成果和經驗后，本課題組提出了一種如圖1所示的RCS盒式節點，該類節點由鋼梁端板、內部鋼腹板、外部鋼側板焊接成為一個整體，對節點區混凝土形成有效約束，鋼梁與端板通過焊接連接；腹板開孔增強了與混凝土的黏結和剪力傳遞，同時方便混凝土澆筑；混凝土柱的縱向鋼筋可穿越節點，節點內無需配置箍筋。試驗已驗證了該類節點的有效性[11]，但其傳力機理及節點承載力計算方法還有待研究。本文在試驗研究成果的基礎上，通過理論分析和數值模擬相結合的方法，對該節點受力機理及抗剪計算方法進行了研究，以期對RCS混合結構的推廣與應用提供有益參考。

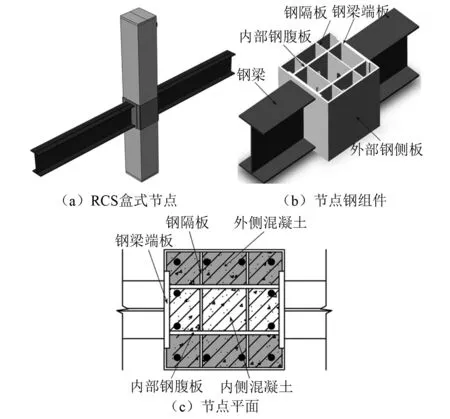
圖1 RCS盒式節點構造Fig.1 Construction of RCS box-type joints

在傳統RCS混合結構節點受力的理論模型中，節點抗剪承載力主要是由鋼梁腹板及混凝土斜壓桿提供[12]，由盒式節點試驗中組件應變分布的特點可類比的認為此類節點抗剪承載力主要由如圖2所示兩部分提供：其一是由內部鋼腹板、外部鋼側板以及鋼梁端板共同構成的鋼組件；其二是節點區外部鋼側板包裹的內、外側混凝土組件。為驗證以上抗剪機理的有效性，本文基于試驗中鋼組件的應變分布及變化趨勢、數值模擬結果對節點抗剪性能及承載力貢獻深入探究，并推導了節點抗剪承載力計算公式。

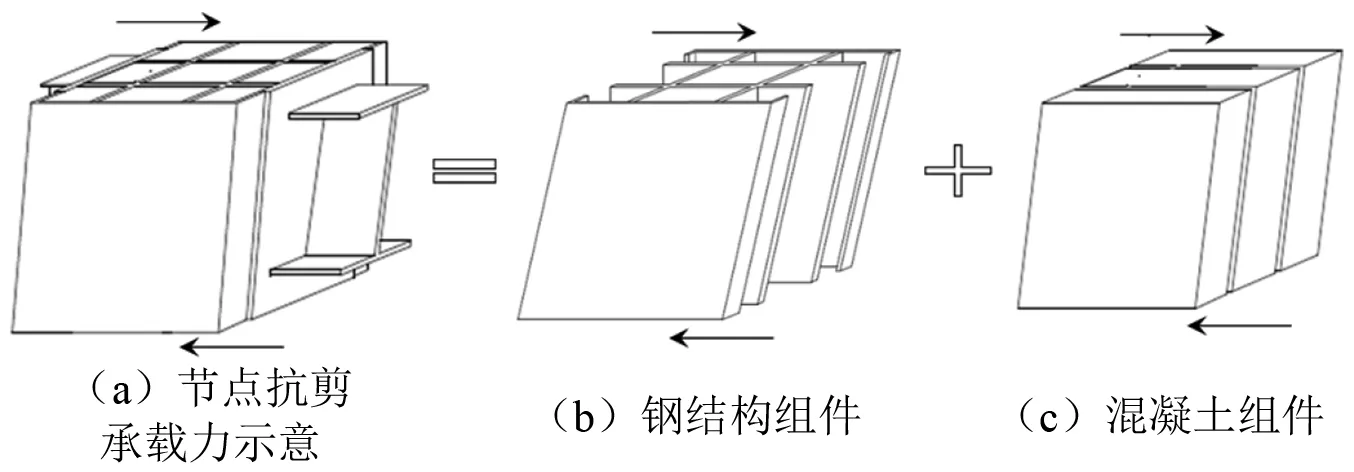
圖2 節點抗剪承載力組成Fig.2 Components of shear bearing capacity of joints

1 節點抗剪機理分析

1.1 基于試驗結果的抗剪機理分析

試驗以RCS 混合框架結構在水平荷載作用下相鄰梁柱反彎點之間的典型單元作為研究對象，考慮內部鋼腹板厚度、間距以及梁端是否附加蓋板加強等主要影響因素制作了4個足尺節點試件RCSJ-1～RCSJ-4，通過對4個試件進行擬靜力試驗，研究了此類節點的受力特點、破壞特征和滯回性能。試驗時位移角幅值分別為1/200(11.6 mm)，1/150(15.5 mm)和1/100(23.3 mm)時4個試件各組件測點的最大應變，如表1所示。由表1可知：在位移角幅值為1/200(11.6 mm)時RCSJ-4鋼梁翼緣屈服；在1/150(15.5 mm)時RCSJ-2內部鋼腹板接近屈服；在1/100(23.3 mm)時所有試件的內部鋼腹板都接近或已屈服。4個試件最大應變均出現在鋼梁翼緣處，其次為內部鋼腹板，可見內部鋼腹板是節點承載力的主要貢獻者。由循環位移為±15.5 mm 時內部鋼腹板的主拉應變和方位角可知，試件RCSJ-1和RCSJ-3的內部鋼腹板均體現為斜向軸線上受力，表明內部鋼腹板主要受剪力作用。

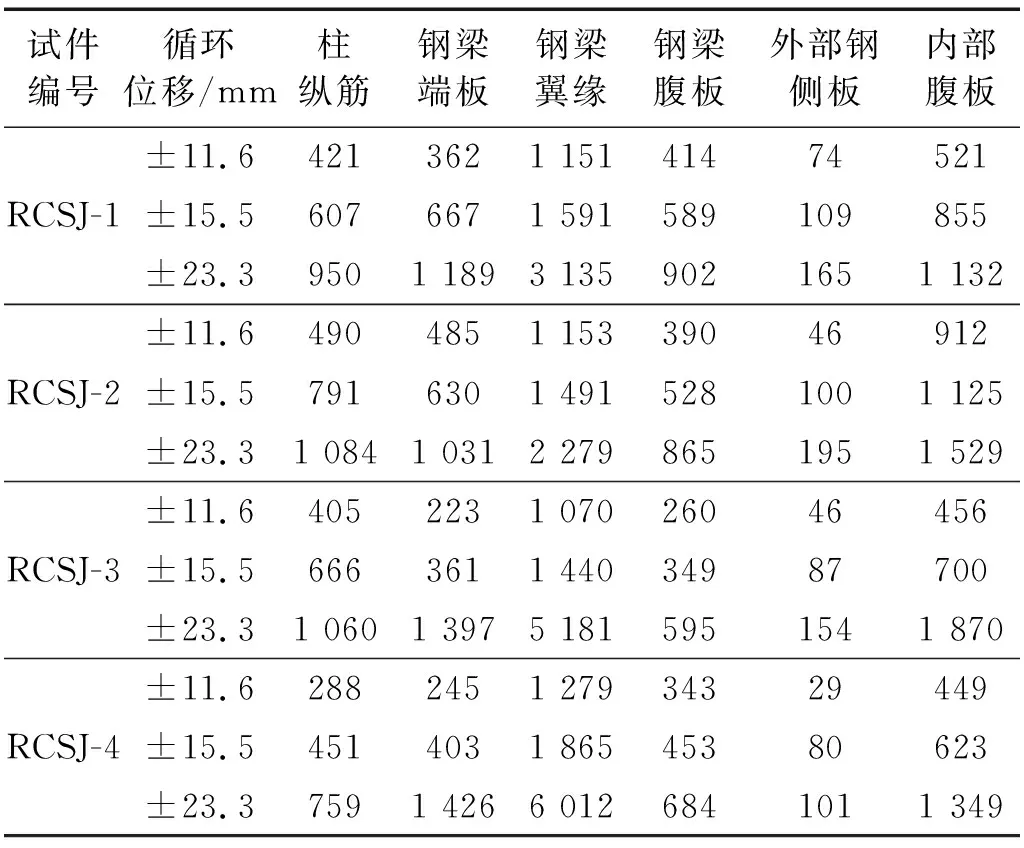
表1 試件鋼組件各測點應變最大值Tab.1 Maximum strain values at each measuring point of specimen assembly 單位：με

試件在加載初期處于彈性狀態，內部鋼腹板和外部鋼側板應變較小，均未達到屈服應變，此時鋼組件承擔很小一部分剪力，如圖3(a)、圖3(b)所示。圖3中：ε為鋼材應變；Δ為位移幅值。隨著位移角幅值增大，節點區內部鋼腹板應變開始加快增長，承擔剪力比重逐漸增大，起到主要抗剪作用。當位移角幅值到達1/50(±46.6 mm)時，內部鋼腹板基本處于屈服狀態，外部鋼側板應變增長迅速但未達到屈服狀態，說明外部鋼側板主要是起約束作用和部分抗剪作用。參考表1與圖3(c)，外部鋼側板應變為內部腹板的0.05～0.20 左右，說明其所受應力作用相對于內部腹板來說處于較低水平。

圖3 不同位移幅值下試件外部鋼側板和內部鋼腹板最大應變及兩者應變比Fig.3 The maximum strain and strain ratio of outer steel side plates and inner steel webs under different displacement amplitudes

1.2 基于數值模擬的抗剪機理分析

為進一步研究RCS盒式節點的傳力途徑和抗剪機理，本節在試驗的基礎上，通過數值模擬研究各組件的受力機理，為抗剪公式的建立提供依據。

1.2.1 模型及驗證

本文選用ABAQUS有限元軟件，基于適用低圍壓下反復加載的塑性損傷混凝土本構模型[13]和GB 50010—2010《混凝土結構設計規范》[14]中建議的混凝土單軸受拉和單軸受壓應力-應變關系建立有限元模型，其中流動法則中混凝土的膨脹角對混凝土受力表現的影響較為明顯，取30°[15]，黏滯系數對結構的剛度影響較大，此處取0.000 5[16]。型鋼及鋼筋均采用雙線性強化模型，本模型考慮了內部鋼腹板、鋼梁端板以及外部鋼側板與節點區混凝土之間的相互作用，由界面法線方向的接觸和切線方向的黏結滑移構成，法線方向的接觸采用硬接觸，切線方向采用庫倫摩擦模型。

下面對產生典型節點區剪切破壞的構件RCSJ-1進行有限元模擬分析，以驗證該模型對于此類節點的適用性。參考蔣麗忠等[17-19]對RCS節點的有限元驗證方法，將模擬所得的滯回曲線、骨架曲線與試驗結果進行對比，如圖4所示。圖4中，P為荷載幅值。整體而言，ABAQUS軟件模擬結果與試驗結果吻合良好。驗證模型的有效性后，結合數值模擬結果探討RCS混合節點各部件對于抗剪承載力的貢獻，并構建了考慮鋼組件及混凝土組件共同工作的RCS混合節點抗剪機理。

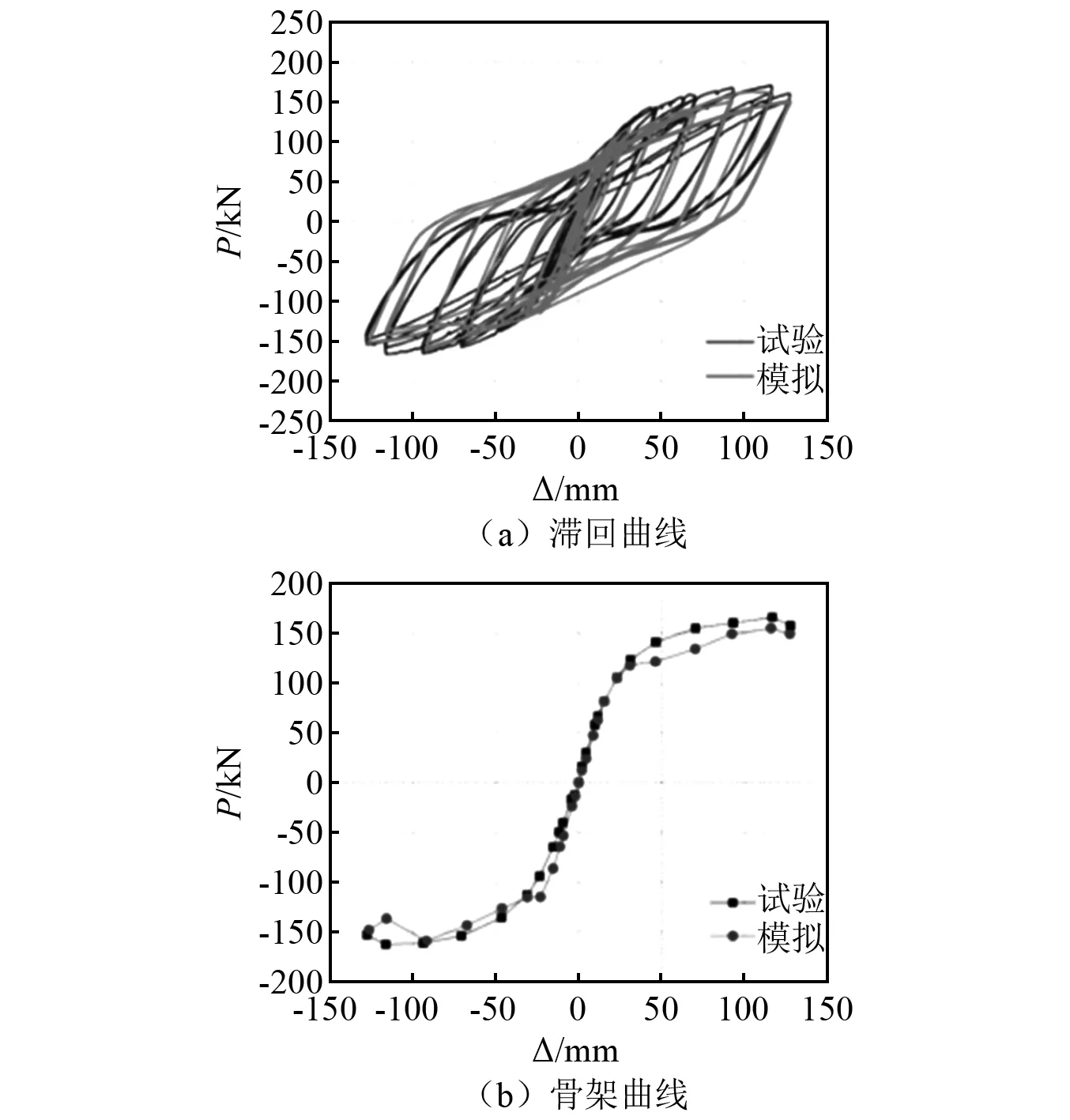
圖4 構件RCSJ-1模擬與試驗結果對比Fig.4 Comparison between simulation and test results of RCSJ-1

1.2.2 節點區鋼組件受力

為研究節點鋼組件的受力機理，提取有限元分析中該部分承載力極限狀態下的應力分布，如圖5所示。由圖5可知，鋼梁端板與非受力方向的鋼隔板的應力水平遠小于受力方向的內部鋼腹板，從鋼梁翼緣傳來的剪力主要由內部鋼腹板與兩側的外部鋼側板共同承擔，鋼梁端板及鋼隔板對抗剪承載力的貢獻可以忽略不計。在柱軸壓力作用下，內部鋼腹板與外部鋼側板均處于剪應力與壓應力共同作用狀態。鋼梁端板的主要作用是將兩端鋼梁傳來的內力傳遞到節點區；鋼隔板主要作用在于將腹板與兩側外部鋼側板相連，使之形成空間整體；同時與內部鋼腹板圍合使節點區混凝土處于三向受壓狀態，從而提高混凝土的抗壓強度。

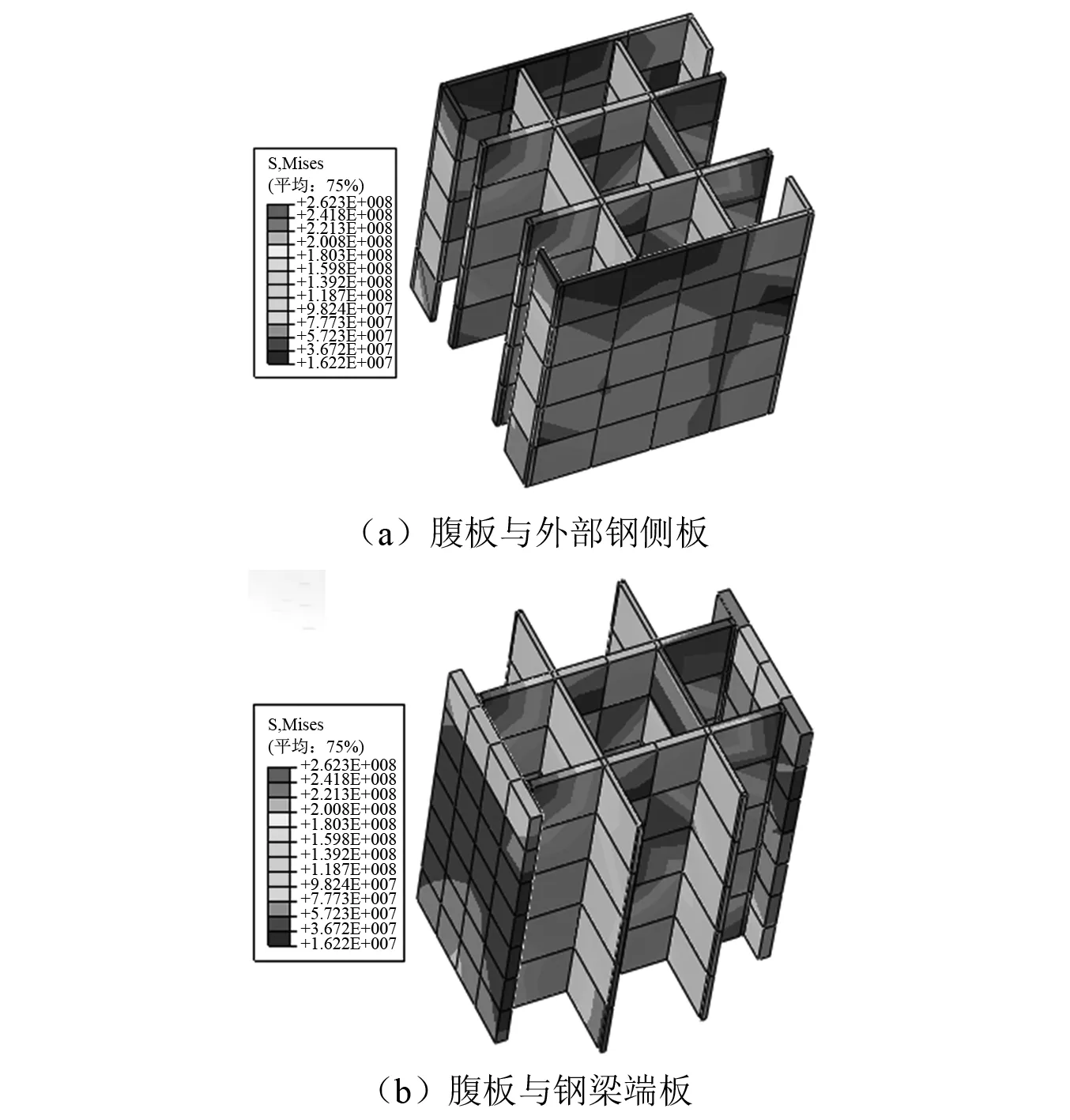
圖5 RCS節點區鋼組件應力云圖Fig.5 The distribution of steel structure part of RCS joints

1.2.3 節點區混凝土組件受力

節點區混凝土屈服點與峰值點的塑性損傷，如圖6所示。由圖6可知，在屈服點時刻，腹板之間的內側混凝土塑性損傷明顯高于其他部位的塑性損傷。隨著位移角幅值的不斷增大，節點區腹板剪切變形加大，在鋼隔板的帶動下，兩側的混凝土也逐漸出現塑性損傷，內部鋼腹板間的內側混凝土塑性損傷最為嚴重，外側混凝土次之。因此，除了內側混凝土起主要的抗剪作用外，外側混凝土的作用也不可忽略。由數值模擬結果圖7可知，外側混凝土應力分布并不均勻，呈現中間大兩邊小的趨勢，且混凝土的抗壓強度未完全發揮，各個模型外側混凝土中間平均主壓應力如表2所示，中間平均主壓應力僅有15 MPa左右，而兩邊壓應力僅有5～9 MPa左右。

圖6 混凝土塑性損傷分布Fig.6 Plastic damage distribution of concrete

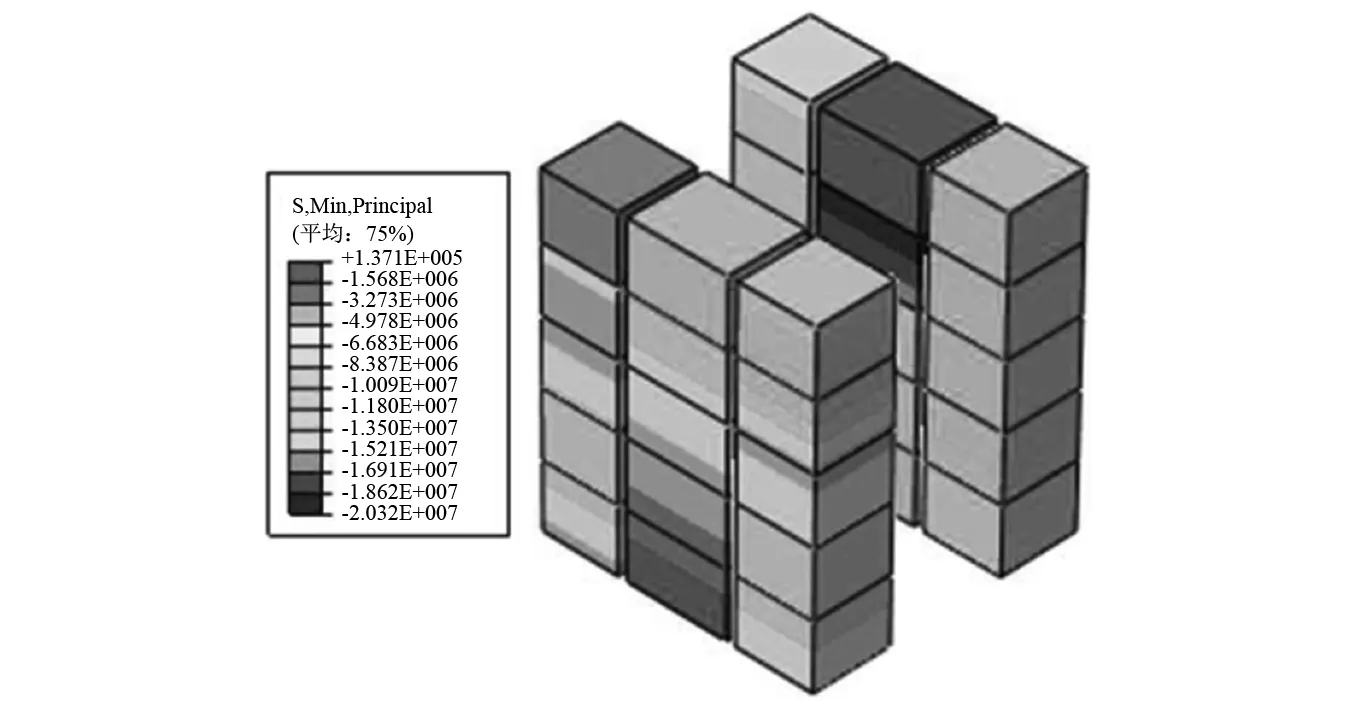
圖7 節點區外側混凝土主壓應力分布圖Fig.7 Distribution diagram of main compressive stress of concrete outside joint area

表2 各模型外側混凝土中間平均主壓應力Tab.2 Average principal pressure stress of concrete in the middle of each component 單位：MPa

在承載力極限狀態時節點區內側和外側混凝土主壓應力矢量圖，如圖8所示。由圖8可知，節點區內、外側混凝土處于明顯的斜向受壓狀態，因此本文考慮采用“斜壓桿”理論對混凝土組件進行分析。鋼梁兩端翼緣的壓應力通過梁端板的擴散作用，將這部分壓應力傳至節點區混凝土的角部區域，與此同時，相鄰柱端受壓區混凝土的豎向壓應力，在抵消了部分梁端剪力之后，傳導至混凝土的角部區域。兩個垂直方向的壓應力合成后，沿節點區對角線方向傳遞，左上角的合力與右下角的合力在斜壓桿內相互平衡，從而形成斜壓桿機構。

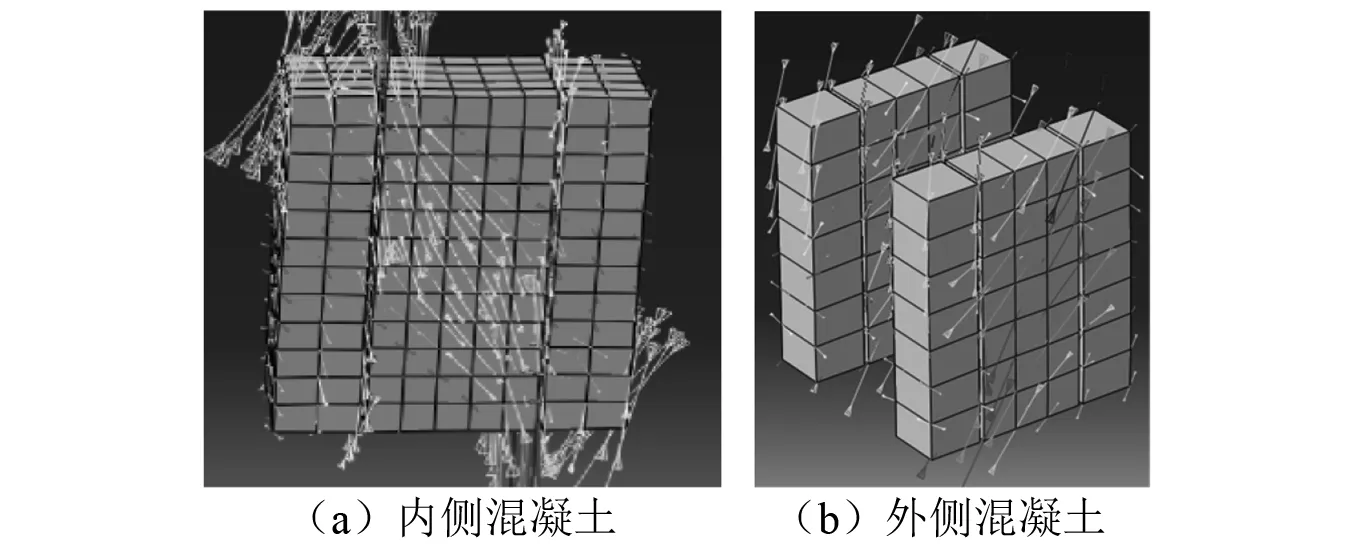
圖8 混凝土主壓應力矢量圖Fig.8 Main pressure stress vectordiagram of concrete

至此，總結以上分析可以認為，RCS混合節點的抗剪承載力主要由節點區鋼組件部分和內、外側混凝土斜壓桿機構兩部分共同構成，如圖9所示。

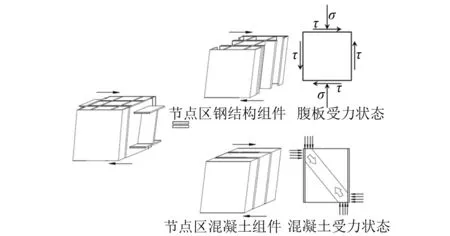
圖9 RCS混合節點抗剪機理Fig.9 Mechanism of shear resistance of RCS joints

2 節點抗剪承載力計算

目前RCS混合節點的抗剪承載力公式主要有美國土木工程師協會(American Society of Civil Engineers,ASCE)RCS混合框架節點設計指南建議公式[20]、我國型鋼混凝土混合結構技術規程(JGJ 138—2016《組合結構設計規范》)計算公式[21]和日本建筑學會(Architectural Institute of Japan,AIJ)RCS節點設計準則推薦公式[22]，其中ASCE公式分別考慮了鋼梁腹板項、內側混凝土斜壓桿項、外側混凝土項以及箍筋項對節點抗剪承載力的貢獻，并采用直接疊加的方法將幾部分組合起來；我國與日本公式則把節點區混凝土作為一個整體，認為節點剪力由混凝土、鋼梁腹板和箍筋三部分承擔[23]。由于很難做到將各個受力部分在不同受力階段所貢獻的節點剪力份額進行篩分，故本文參考國內外學者常用手段，基于試驗與數值模擬結果，建立半經驗半理論的RCS混合節點抗剪承載力計算公式。

2.1 節點區鋼組件抗剪承載力

由試驗數據及有限元分析可知，當節點達到峰值狀態時，內部鋼腹板基本進入全面屈服狀態，而外部鋼側板此時還處于較低的應力水平，因此，需分開考慮兩部分對節點區的抗剪貢獻。

2.1.1 內部鋼腹板抗剪承載力

對于內部鋼腹板，由于軸壓力的存在，使其處于壓應力和剪應力共同作用的狀態，其受力情況如圖10(a)所示。其中，σ為柱傳來的軸壓應力。

內部鋼腹板處于彈性狀態時，其主拉應力σ1和主壓應力σ3如式(1)所示(此時主壓應力σ2=0)，達到極限狀態前適用式(2)所示的Mises屈服條件

(1)

(2)

式中：σy為內部鋼腹板抗拉屈服強度；τ為剪應力。將式(1)代入式(2)，可得內部鋼腹板剪切屈服應力τy為

(3)

由式(3)可知，軸壓應力將降低內部鋼腹板的抗剪承載能力，因此引入軸壓應力不利影響系數φ，參考易勇[24]的研究成果，偏安全考慮取φ=0.8。同時根據Parra-Montesinos等[25]相關研究，在靠近腹板邊緣區域存在一定的應力下降，應力分布如圖10(b)所示，其中hc為節點水平截面高度。

綜合以上因素，可得內部鋼腹板所貢獻的抗剪承載力表達式(4)

(4)

式中：τweb為內部鋼腹板應力；σy采用腹板抗拉強度設計值fy；tw為內部鋼腹板厚度。

2.1.2 外部鋼側板

通過1.2.2節對于外部鋼側板的分析可知，外部鋼側板在受力過程中直接承擔了一部分節點剪力，但其應力水平較低，對節點區抗剪承載力的貢獻難以直接計算。試驗過程中RCSJ-1～RCSJ-4試件外部鋼側板中部與內部鋼腹板中部在試件開裂、屈服與承載力極限狀態下的平均應力比，如圖11所示。從構件開裂到構件屈服階段，外部鋼側板處于較低的應力水平，內部鋼腹板起主要抗剪作用，外部鋼側板與內部鋼腹板的應力比處于0.25～0.30；構件屈服之后，外部鋼側板逐漸發揮抗剪作用，因此應力比增加到0.33～0.37。可以看出，內部鋼腹板與外部鋼側板的應力比處于一個相對穩定的區間，因此參考Deierlein等[26]對混合節點試件中擴展式面承板的研究方法，擬分析不同節點中二者貢獻剪力的相對比例，根據規律總結外部鋼側板對于節點抗剪承載力的貢獻份額，引入放大系數β來反映外部鋼側板對于節點抗剪承載力的貢獻。

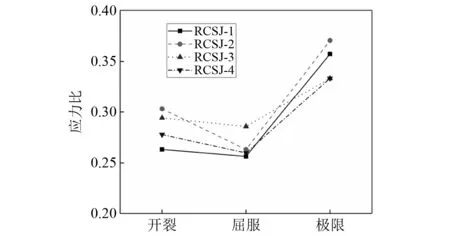
圖11 各試件外部鋼側板與內部鋼腹板平均應力比Fig.11 Average stress ratio of external steel side plate and internal steel web of each test piece

外部鋼側板厚度分別為2 mm，4 mm和6 mm的有限元模型在極限狀態下內部鋼腹板中部與外部鋼側板中部的平均應力及其承擔的剪力，如表3所示。其中外部鋼側板考慮采用與內部鋼腹板相同的受力分析思路。

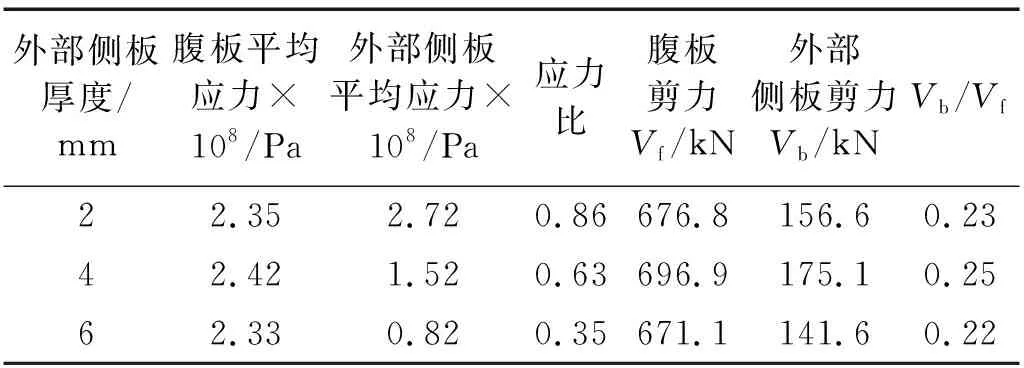
表3 不同外部側板厚度下外部側板與腹板平均應力及其承擔的剪力Tab.3 Average stress and shear force of external side plate and web under different external side plate thickness

由表3可知，當外部鋼側板厚度不同時，其為節點區貢獻的抗剪承載力與腹板為節點區貢獻的抗剪承載力之比維持在0.22～0.25，因此，可以認為引入一個考慮外部鋼側板作用的抗剪承載能力放大系數β是合理可行的，偏安全考慮取該比例的下限0.2，故盒式節點放大系數取為β=1.2。

綜上所述，內部鋼腹板及外部鋼側板對節點區貢獻的抗剪承載力表達式可表示為

(5)

式中，fy為抗拉強度設計值。

2.2 節點區混凝土

2.2.1 內側混凝土

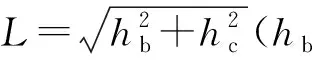
Vc1=fcH(d-tw)cosθ=0.3fchc(d-tw)

(6)

式中：d為內部鋼腹板間距；fc為混凝土抗壓強度。

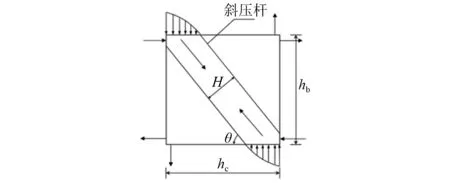
圖12 混凝土斜壓桿模型示意圖Fig.12 Schematic diagram of concrete diagonal strut model

2.2.2 外側混凝土

外側混凝土也采用與內側混凝土相同的分析方法，將其考慮成兩個斜壓桿。由機理分析可知外側混凝土應力呈現中間大兩邊小的分布特點，且混凝土的抗壓強度未完全發揮，將外側混凝土的應力分布近似考慮為圖13所示的分布規律，其中則由外側混凝土貢獻的節點區剪力為

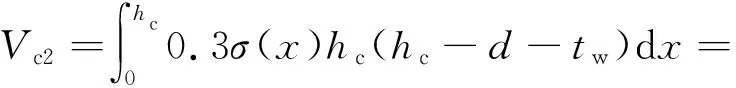
(7)

式中，σ(x)為混凝土壓應力。

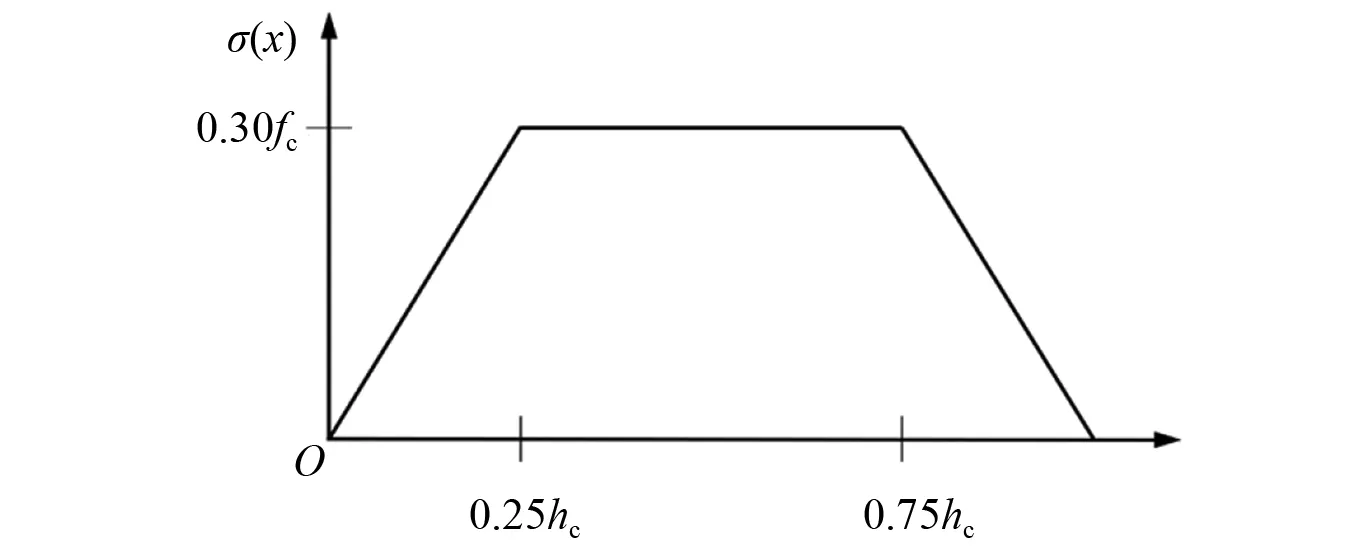
圖13 外側混凝土壓應力近似分布Fig.13 Approximate distribution of compressive stress in outer concrete

將處于承載力極限狀態的內部鋼腹板、內側混凝土與尚未屈服的外側混凝土進行疊加即可得到RCS盒式節點的抗剪承載力計算公式

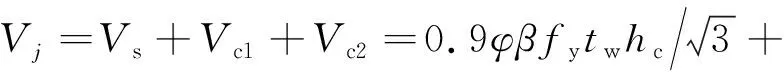
(8)

式中，Vs為內部鋼腹板貢獻的抗剪承載力。

3 公式驗證

分別應用第2章提到的常用公式以及本文推導式(8)進行試件RCSJ-1～RCSJ-4抗剪承載力計算，試件抗剪承載力試驗值Vt與計算值Vj對比如表4、表5所示，其中材料強度采用實測均值。從表4、表5可知，美國ASCE、日本AIJ和我國JGJ 138—2016《組合結構設計規范》給出公式的計算值與試驗值相比均偏大，主要原因在于美國ASCE計算公式認為整個內部鋼腹板為純剪狀態而未考慮軸壓力對抗剪承載力的削弱；我國JGJ 138—2016《組合結構設計規范》與日本AIJ公式未區分節點區內側混凝土與外側混凝土而高估了節點區混凝土的抗剪承載力。本文推導公式的計算結果與試件的實際抗剪承載力對比，見表5。表5中：RCSJ-1與RCSJ-2由于節點區發生破壞，因此所得試驗值與計算值非常接近，僅有5%左右的誤差；而RCSJ-3與RCSJ-4由于節點區未發生破壞，所得節點的抗剪承載力試驗值失真，故試驗值小于理論計算值。又由表5可知，內部鋼腹板與內側混凝土對整個節點抗剪承載力貢獻最大，約占總承載力的80%左右。綜上可認為，采用現階段常用的RCS混合節點抗剪承載力公式計算RCS盒式節點偏于不安全；而采用本文推導公式的計算值與試驗值吻合良好，且具有較高的精度。

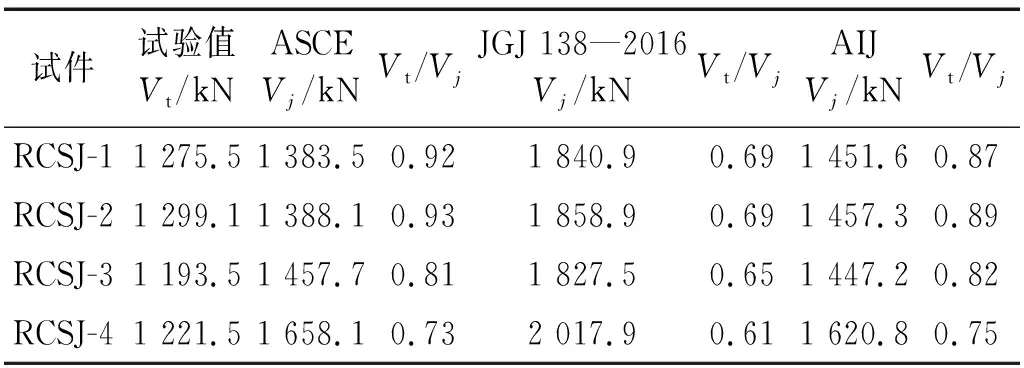
表4 現行RCS節點抗剪承載力公式計算結果Tab.4 Calculation results of current shear capacity formula for RCS joints

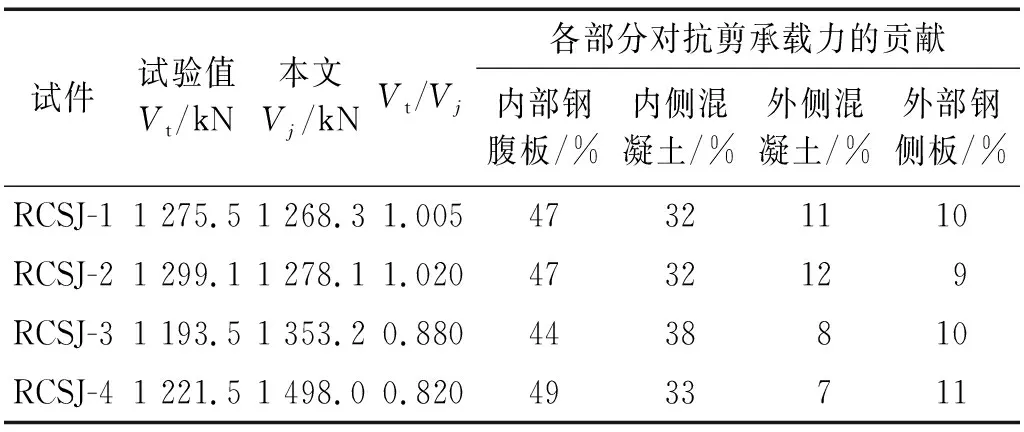
表5 本文RCS節點抗剪承載力公式計算結果Tab.5 Calculation results of shear capacity formula for RCS joints in this paper

為進一步驗證RCS盒式節點抗剪公式的有效性，不同參數條件下有限元模型的抗剪承載力模擬值Vs與公式計算值Vj對比，如表6所示。且當外部側板厚度為0時(取消外部鋼側板)，計算公式中不考慮側板放大系數，即β=1，其中材料強度采用設計值。由表6可知，針對不同的參數條件，有限元模型得到的節點區最大抗剪承載力與按公式計算所得的計算值非常接近，誤差均在4%以內，可認為所提計算公式能較為準確地預測該類RCS盒式節點的抗剪承載力。

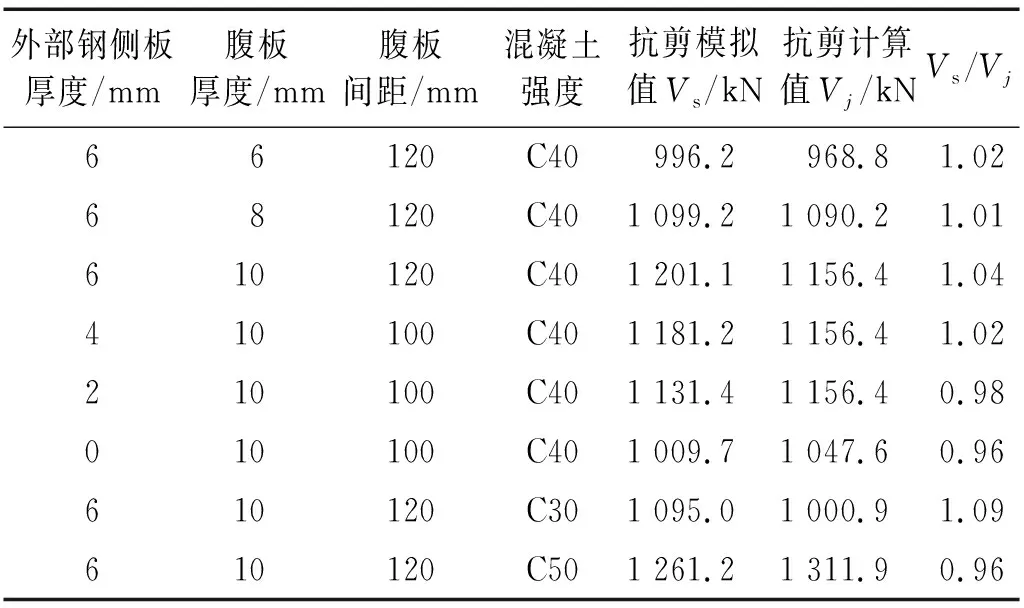
表6 抗剪承載力計算值與有限元模擬值比較Tab.6 Comparison of shear strength between calculation and finite element method

4 結 論

本文基于RCS盒式節點的低周反復荷載試驗結果，利用有限元軟件ABAQUS分析了節點的抗剪機理，建立了該類節點的抗剪承載力計算公式，主要得到以下結論：

(1) 節點剪力由內部鋼腹板、外部鋼側板及內、外側混凝土共同承擔，其中內部鋼腹板和內側混凝土為主要受力部分，其對節點抗剪承載力的貢獻分別占比為50%，30%左右；內部鋼腹板和外部鋼側板表現為剪壓破壞，內、外側混凝土為斜壓破壞。

(2) 在提出的抗剪機理的基礎上，建立了分別考慮內部鋼腹板、外部鋼側板與內外側混凝土抗剪機構貢獻的RCS混合節點抗剪承載力計算公式，對比發現計算值與試驗值吻合良好。同時，利用有限元軟件，通過改變不同的節點區構造參數得到的節點區抗剪承載力與按本文建議公式的計算值有較高的吻合度，說明該公式具有一定的適用性和有效性。