化難為易過(guò)“三關(guān)”

文／曹小龍

二次函數(shù)內(nèi)容豐富，難點(diǎn)頗多，綜合性強(qiáng)，令很多同學(xué)望而卻步。本文列舉三個(gè)方面簡(jiǎn)述突破之法。

一、圖像與性質(zhì)

例1在平面直角坐標(biāo)系中，已知二次函數(shù)y=ax2+bx+c（a≠0）的圖像如圖1所示，有下列5個(gè)結(jié)論：①abc＞0；②2a-b=0；③9a+3b+c＞0；④b2＞4ac；⑤a+c＜b。其中正確的有（ ）。

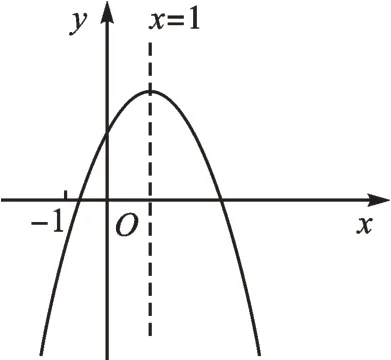
圖1

A.1個(gè) B.2個(gè) C.3個(gè) D.4個(gè)

【分析】由拋物線(xiàn)開(kāi)口方向判斷a與0的關(guān)系，由拋物線(xiàn)與y軸的交點(diǎn)判斷c與0的關(guān)系，然后根據(jù)拋物線(xiàn)對(duì)稱(chēng)性推理判斷。

解：∵圖像開(kāi)口向下，∴a＜0。

∵對(duì)稱(chēng)軸為直線(xiàn)

∴b=-2a＞0。

∵圖像與y軸的交點(diǎn)在x軸的上方，

∴c＞0。∴abc＜0，①錯(cuò)誤。

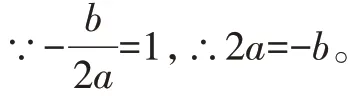
∴2a-b=-2b＜0，所以②錯(cuò)誤。

由圖像可知點(diǎn)（-1，0）關(guān)于x=1的對(duì)稱(chēng)點(diǎn)為（3，0）。

∵當(dāng)x=-1時(shí)，y＜0，

∴當(dāng)x=3時(shí)，y＜0。

∴9a+3b+c＜0，③錯(cuò)誤。

∵拋物線(xiàn)與x軸有兩個(gè)交點(diǎn)，

∴b2-4ac＞0。∴b2＞4ac，④正確。

當(dāng)x=-1時(shí)，y＜0，

∴a-b+c＜0。∴a+c＜b，⑤正確。

∴正確的為④⑤，故選B。

二、模型與應(yīng)用

例2某商品有線(xiàn)上、線(xiàn)下兩種銷(xiāo)售方式。

線(xiàn)上銷(xiāo)售：?jiǎn)渭麧?rùn)定為600元時(shí)，銷(xiāo)售量為0件，單件利潤(rùn)每減少1元銷(xiāo)售量增加1件。另需支付其他成本5000元。

線(xiàn)下銷(xiāo)售：?jiǎn)渭麧?rùn)500元。另需支付其他成本12500元。

注：凈利潤(rùn)=銷(xiāo)售商品的利潤(rùn)-其他成本。

（1）線(xiàn)上銷(xiāo)售100件的凈利潤(rùn)為_(kāi)__元；線(xiàn)下銷(xiāo)售100件的凈利潤(rùn)為_(kāi)__元；

（2）若銷(xiāo)售量為x件，當(dāng)0＜x≤600時(shí)，比較兩種銷(xiāo)售方式的凈利潤(rùn)；

（3）現(xiàn)有該商品400件，若線(xiàn)上、線(xiàn)下同時(shí)銷(xiāo)售，售完后的最大凈利潤(rùn)是多少元？此時(shí)線(xiàn)上、線(xiàn)下各銷(xiāo)售多少件？

【分析】第（2）問(wèn)，先分別求出兩種銷(xiāo)售方式的凈利潤(rùn)的函數(shù)表達(dá)式，再分三種情況討論，可解方程、不等式；也可作差后根據(jù)圖像觀(guān)察求解。第（3）問(wèn)，需建立關(guān)聯(lián)兩種銷(xiāo)售方式的新函數(shù)表達(dá)式，再求最值。

解：（1）45000，37500。

（2）設(shè)銷(xiāo)售量為x件時(shí)，線(xiàn)上銷(xiāo)售的凈利潤(rùn)為y1元，線(xiàn)下銷(xiāo)售的凈利潤(rùn)為y2元，線(xiàn)上線(xiàn)下銷(xiāo)售的凈利潤(rùn)差為w元。則

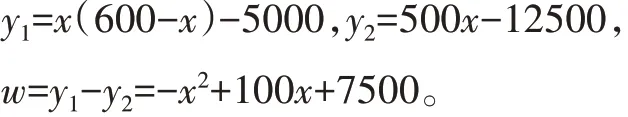
結(jié)合二次函數(shù)w=-x2+100x+7500的圖像可知：

當(dāng)0＜x＜150時(shí)，w＞0，即線(xiàn)上銷(xiāo)售的凈利潤(rùn)大于線(xiàn)下銷(xiāo)售的凈利潤(rùn)；

當(dāng)x=150時(shí)，w=0，即線(xiàn)上銷(xiāo)售的凈利潤(rùn)等于線(xiàn)下銷(xiāo)售的凈利潤(rùn)；

當(dāng)150＜x≤600時(shí)，w＜0，即線(xiàn)上銷(xiāo)售的凈利潤(rùn)小于線(xiàn)下銷(xiāo)售的凈利潤(rùn)。

（3）設(shè)線(xiàn)上銷(xiāo)售a件時(shí)，售完400件商品的凈利潤(rùn)為m元。則

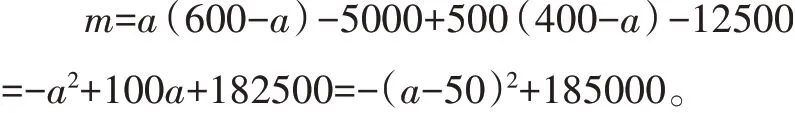
∵m的函數(shù)圖像是拋物線(xiàn)且開(kāi)口向下，∴當(dāng)a=50時(shí)，m有最大值185000，即當(dāng)線(xiàn)上銷(xiāo)售50件，線(xiàn)下銷(xiāo)售350件時(shí)，最大凈利潤(rùn)為185000元。

三、含參與綜合

例3已知函數(shù)y1=x+1和y2=x2+3x+c（c為常數(shù)）。

（1）若兩個(gè)函數(shù)圖像只有一個(gè)公共點(diǎn)，求c的值；

（2）點(diǎn)A在函數(shù)y1的圖像上，點(diǎn)B在函數(shù)y2的圖像上，A、B兩點(diǎn)的橫坐標(biāo)都為m。若A、B兩點(diǎn)的距離為3，直接寫(xiě)出滿(mǎn)足條件的m值的個(gè)數(shù)及其對(duì)應(yīng)的c的取值范圍。

【分析】（1）聯(lián)立方程，通過(guò)判別式Δ=0求解。（2）方法一：分別令y1-y2=3，y1-y2=-3，根據(jù)關(guān)于m的一元二次方程中Δ的取值范圍與c的關(guān)系列方程或不等式求解。方法二：由（1）結(jié)合圖像的平移，尋找臨界位置，數(shù)形結(jié)合定范圍。

解：（1）兩個(gè)函數(shù)圖像只有一個(gè)公共點(diǎn)，則方程x2+3x+c=x+1有兩個(gè)相等的實(shí)數(shù)根，∴Δ=0，即22-4（c-1）=0。∴c=2。

（2）如圖2，當(dāng)c＞5時(shí)，0個(gè)；當(dāng)c=5時(shí)，1個(gè)；當(dāng)-1＜c＜5時(shí)，2個(gè)；當(dāng)c=-1時(shí)，3個(gè)；當(dāng)c＜-1時(shí)，4個(gè)。

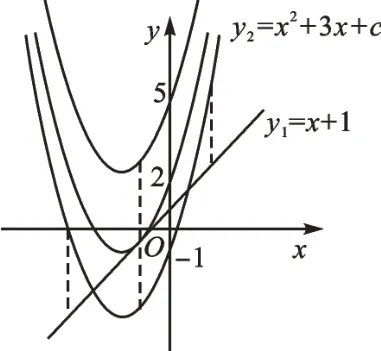
圖2

二次函數(shù)含參問(wèn)題中，我們要思考圖像的對(duì)稱(chēng)軸、與x軸交點(diǎn)及經(jīng)過(guò)的定點(diǎn)能否求出，多畫(huà)幾個(gè)草圖分析臨界位置（如頂點(diǎn)在x軸上時(shí)，經(jīng)過(guò)特殊點(diǎn)——原點(diǎn)、定點(diǎn)或其他已知點(diǎn)），觀(guān)察圖像變化，確定參數(shù)的取值范圍。如a決定形狀、開(kāi)口大小，a的絕對(duì)值越大（小），開(kāi)口就越小（大）等。