把握本質　類比關聯　生成路徑

佘丹 王平

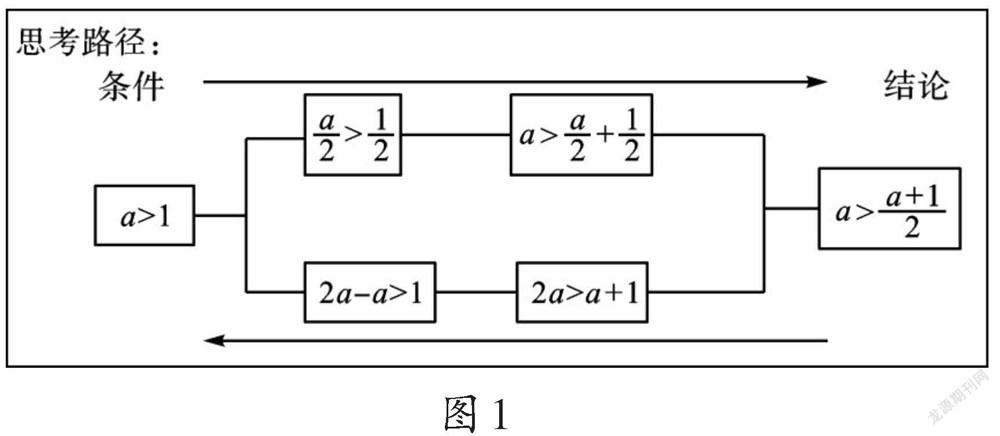
推理能力一直以來都是數學教育的重點關注對象。從推理類型來看，初中推理有幾何推理和代數推理。幾何推理以圖形為載體，形象直觀；代數推理側重數和式的變形和轉換，相對比較抽象，是學生數學思維向更高層次發展的必備能力。《義務教育數學課程標準（2022年版）》指出：要關注基于代數的邏輯推理，讓學生在邏輯論證的過程中，逐漸形成推理能力，培養科學精神。因此，教師在初中數學教學過程中，有必要進行點面結合、系統推進，逐步滲透代數推理。下面，本教學案例立足于代數內容的自身特點，把握代數推理的本質，類比幾何推理的思維方式，在發展學生代數推理能力的路徑與策略上做出了一些探索，現與讀者分享。

一、教學過程

1.類比探究

師：生活中除了有相等關系，還有許多的不等關系。從相等關系中我們抽象出了等式的概念，從不等關系中我們抽象出了不等式的概念。那么，等式有等式的性質，不等式有哪些性質呢？

師追問1：我們先回顧一下，等式有哪些性質？它的符號語言是什么？

師追問2：類比等式的基本性質，你覺得不等式的基本性質可能是什么？

師追問3：這些都是大家的猜想，請舉例來證明。

［設計意圖］在學生回顧等式的基本性質的符號語言時，教師從命題的角度引出用“條件……，結論……”的形式，幫助學生明確性質中的條件和結論，為不等式的基本性質的條件和結論作鋪墊。類比等式的基本性質，猜想不等式的基本性質，這樣的類比猜想是對知識的遷移與拓展，是研究新問題的重要思想方法。