基于數學文化的數學閱讀教學策略研究
——以“一元二次方程配方法”為例

鄭麗生

（仙游第一中學，福建 仙游 351200）

數學閱讀是指圍繞數學問題或相關材料，以數學思維為基礎和紐帶，用數學的方法，觀念來認知、理解、汲取知識和感受數學文化的學習活動。數學閱讀教學以學生為主體，以培養學生數學閱讀能力為目標，聚焦核心素養，進而提高課堂效率［1］。然而，許多學生在進行數學閱讀時，經常會出現閱讀偏差或無法讀懂數學材料的現象。其根本癥結在于在欠缺數學閱讀方法和閱讀中的思考能力。本文以“一元二次方程配方法”為例，談談在初中數學課堂中基于數學文化的數學閱讀教學的一些思考。

一、拓展數學教材內容，創建數學文化關聯閱讀

數學閱讀教學首先要立足于教材，通過對教材基礎知識內容進行適當的拓展，創建關聯數學文化閱讀，進而建立新知與舊知間的聯系。同時，依據同化理論，構建主題內容的知識體系，促進新知識的學習。

如人教版九年級數學教科書中的“配方法”，既是一元二次方程的解法基礎，也是求根公式的依據。以往“配方法”的教學往往只注重配方法的基本步驟，對“配方法”的推導證明關注較少，且推導多采用數的結構特征，很少體現數形結合的數學思想，以及數學閱讀和數學語言的轉化。按照“配方法”的基本步驟解題雖然容易理解，但存在不符合數學知識發生、發展的歷史序；不利于理解圖形語言和符號語言的相通性;不利于學生知識與思想的銜接發展等問題。因此，在一元二次方程配方法教學中，可設計“古巴比倫的祭司給出的配方法幾何證明方法”“趙爽的配方法幾何證明方法”“婆什迦羅用配方法解二次項系數不為1 的一元二次方程”等相關歷史溯源閱讀。

如可編寫“古巴比倫的祭司給出的配方法幾何證明方法”課前閱讀探究性學案，通過挖掘關聯的數學文化閱讀資料，設計生動有趣、揭示知識本質的探究性問題，并把數學思想方法融入情境之中（見表1）。

表1

課后可布置學生用不同方法搜集整理數學文化閱讀資料以及閱讀策略。這樣，學生不僅可了解更多的證明方法，而且對各種方法進行相互比較，進而領會不同證明方法背后的數學思想。閱讀材料中可設置開放性問題，啟導學生將知識延伸拓展，完善思維認知結構。

二、發展數學符號意識，提升數學閱讀感悟力

《義務教育數學課程標準（2022 年版）》提出“會用數學的語言表達現實世界”的要求。因此，發展數學符號意識是數學閱讀的前提保障。數學閱讀教學的主要難點在于學生對數學語言的抽象性、簡約性、概括性的理解與掌握。基于數學文化的數學閱讀教學中，可以先讓學生對數學文化閱讀材料進行歸納總結，并用數學符號表達出其中的數形關系、變化規律等。教師通過多媒體圖像展示，降低數學語言的抽象程度，增加直觀性、生動性，發展數學符號意識，提升數學閱讀感悟力。

如，以下圖形解法形象地展示一元二次方程的配方過程。請同學借助矩形紙片操作觀察，用符號語言解釋圖形的解法，對幾何圖形的解方程進行解釋（如圖1）。為什么要割出邊長為3 的長方形？通過填空，你發現了什么？（小組合作交流反饋）

圖1

這一設計一方面遵循了歷史發展順序，有助于學生認清問題的實質、明確解題的思路，另一方面用直觀的圖形語言，從形的方面演示了配方的過程，并用簡潔的符號語言，從數的方面解釋了轉化的過程，從而拓寬了學生的數學思維。

三、重新經歷數學文化實驗操作，促進數學閱讀再創造

數學實驗操作是連接思維與動作之間的橋梁，可有效啟發解決同類問題的思路和方法，對思維再創造起著重要的推動作用，從而促進學生關聯性思考，培養發散思維。

如在一元二次方程的配方法教學中，教師可作如下設置：首先，讓學生重新經歷數學古巴比倫的數學實驗操作的過程，把長方形通過割、補、拼，接成一個大的正方形。以一元二次方程求面積為例，把它看作是長為（x+6）、寬為x、面積為55 的矩形。其次，設計啟發性問題，讓學生動手操作，并用數學符號語言描述幾何變形過程，觀察數與形的變化規律。然后，引導學生描述幾何圖形的變化與符號語言表達的形式變化和規律，整個圖形變形的過程就是配方過程的幾何化。接著，探討配方法的規律。即對二次項系數為1 的一元二次方程配方時，一般在方程兩邊各加上一次項系數一半的平方。體會從特殊到一般、數形結合思想在數學學習中的重要作用。最后，設置數學文化應用探究性問題：

問題1：用不同的拼圖方法描述配方法解一元二次方程（如圖2、3）。

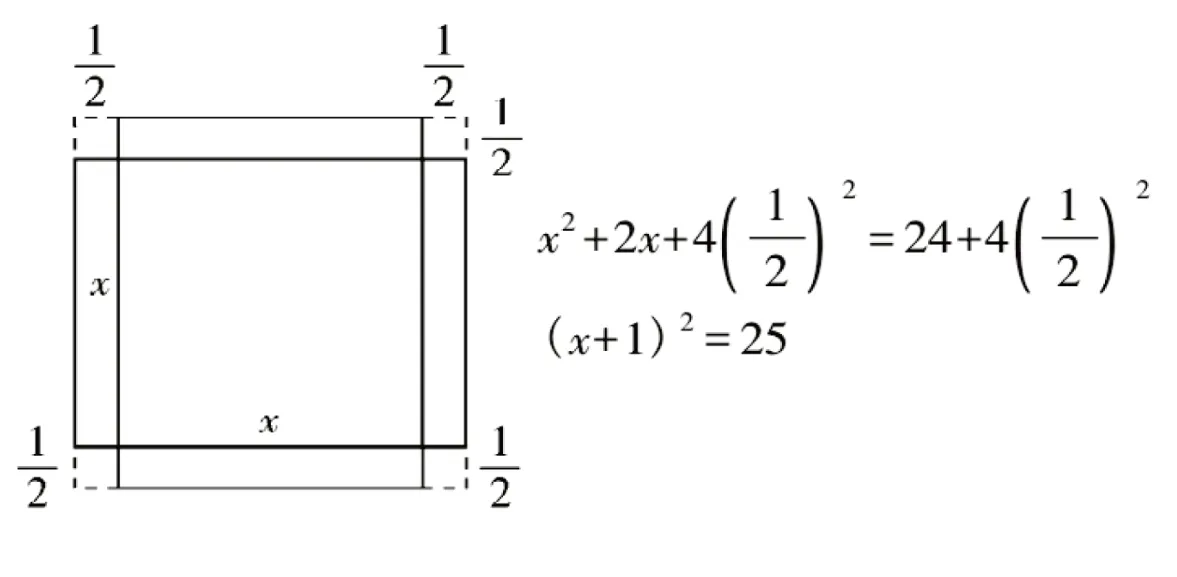
圖2

問題2：用拼圖的方法描述配方法解二次項系數不為1 一元二次方程（如圖4）。

圖4

至此，學生的數學文化閱讀學習從單純接受、模仿熟練轉變為自主閱讀、探究發現、創新應用。師師、師生、生生合作被有效激發，從而達到教學相長。

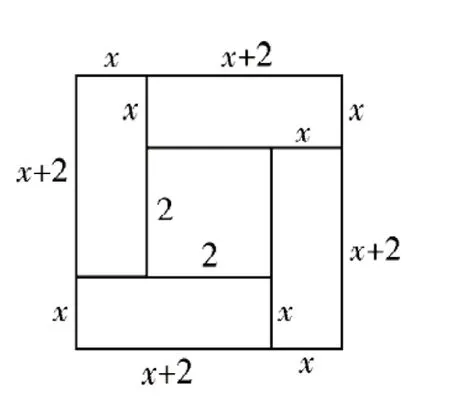
圖3

數學閱讀教學要求教師在學生前面“領跑”，要善于開發相關閱讀資料、創新科學有效的閱讀方法，要積極引導學生的數學閱讀學習從單純接受、模仿熟練轉變為自主閱讀、探究發現、創新應用。基于數學文化的數學閱讀能力培養是一個循序漸進的過程，需要師師、師生、生生合作激發，以達到教學相長。