基于神經網絡和散射中心模型的目標參數提取

羅宇航, 陳彥錫, 郭琨毅, 盛新慶, 馬 靜

(1. 北京理工大學信息與電子學院應用電磁研究所, 北京 100081; 2. 北京仿真中心, 北京 100854)

0 引 言

散射中心建模目前是目標散射特性研究領域的熱門方向之一。采用少量帶屬性的散射中心散射場的疊加可以精確仿真擴展目標的散射特性,因此基于散射中心模型的散射仿真非常高效。同時，散射中心特征與雷達圖像特征直接對應,因此該方法在雷達成像仿真、目標特征提取、自動目標識別等領域具有較高的實用價值[1-3]。散射中心建模方法可以分為正向方法和逆向方法兩種,正向方法依據電磁計算方法以及散射貢獻分離的方法,直接獲得各散射中心的散射場,進而建立參數化模型[4];逆向方法先利用參數化模型表示目標上各散射中心的散射場,然后采用參數估計方法從目標散射場或成像結果通過估計或提取得到模型的參數[5]。逆向方法不需要電磁計算過程,利用通用的參數估計工具即可實現。

散射中心研究一直伴隨著雷達技術的發展,在以低分辨率雷達為主流的時期主要用點目標來模擬目標散射波。而近些年來，由于高分辨雷達的出現，點目標模型已經不能滿足目標特征識別的需求。因此,為了精確描述雷達高分辨圖像呈現的特征,出現了帶有頻率、方位依賴性描述的散射中心模型。這些帶有屬性的散射中心模型可以描述目標強散射源的位置分布、散射幅度起伏等。散射中心的參數提取是如今散射中心的重要研究內容之一,遺傳算法、粒子群方法等雖然在散射中心參數估計中被廣泛應用[6-8],但其往往計算復雜，耗時量大,而神經網絡可以有效地解決類似的逆向問題。

卷積神經網絡(convolutional neural network,CNN)是在深度學習中應用最為廣泛的一類網絡,眾多CNN模型在圖像分類、目標檢測等領域取得了突破性的成果。如采用單層卷積神經網絡對高分辨一維距離像、合成孔徑雷達(synthetic aperture radar,SAR)圖像進行特征自動識別[9-10],利用雙向卷積-循環網絡來提取目標特征[11]。采用預訓練的CNN模型到其他數據集做遷移學習,并重新學習目標集特征[12-13]。目標識別傳統方法需要大量的己標注訓練樣本數據,需要不同尺寸目標的全方位散射數據,而采用數值法計算目標的散射非常耗時,可見充足的訓練樣本非常難以獲得。為此,本文利用已知幾何結構目標的散射中心模型快速生成訓練樣本。以彈頭目標為例,由散射中心模型模擬得到的散射場時頻像與全波法結果相比,相關系數可以達到90%以上。因此，將可替代數值計算結果用作訓練樣本,可極大地節約獲得訓練樣本所需的計算資源和時間。

對于雷達目標的幾何參數提取,傳統方法多是利用目標的SAR圖像或逆合成孔徑雷達(inverse SAR, ISAR)圖像來獲取,目標的幾何參數獲取較為困難[14-15]。前饋神經網絡(back propagation neural network, BPNN)是一種按誤差逆傳播算法訓練的多層前饋網絡,其網絡結構相對簡單,可以逼近非線性函數,可用于多種情景下的參數預測[16-18]。利用散射中心模型快速生成的訓練數據作為輸入,通過改變網絡的具體結構來訓練得到目標幾何參數。

本文利用神經網絡以及散射中心模型,快速實現自動目標類型識別,以及從目標散射中自動逆向提取目標幾何參數。以常見的錐-柱-臺結構彈頭目標為例,通過改變散射中心的參數,快速得到多種結構、不同尺寸的目標的大量訓練數據,利用CNN識別出目標類型,再用BPNN預測輸出目標的幾何參數。經數值實驗,驗證了網絡具有較高的識別率,而且預測輸出的幾何參數結果與實際幾何尺寸具有較高的一致性。該方法可以推廣至其他結構相似、尺寸不同的目標類型,具有較高的應用價值。

1 彈頭類目標的散射中心模型及其時頻像特征

屬性散射中心模型是目前應用最為廣泛的散射中心模型。它的提出為描述復雜目標電磁散射特性提供了簡明、有效的技術手段。散射中心的屬性參數包括幅度、位置以及其對方位、頻率、極化的依賴性等。依據散射中心的位置分布特征，散射中心可以分為分布型散射中心(distributed scattering center,DSC)(如位于平面、單曲面、長直棱邊)、局部性散射中心(local scattering center,LSC)(如位于尖頂、小圓頂等)和滑動型散射中心(sliding scattering center, SSC)(如位于雙曲面、曲邊等)。散射中心模型的部分參數與目標的幾何結構直接相關,如DSC的分布長度為平面或單曲面、長直棱邊的長度,SSC的位置軌跡為目標的幾何輪廓。因此,通過提取散射中心的參數可以在一定程度上反演出目標的幾何尺寸[3]。

時頻像在散射中心特征分析中被廣泛采用。由于時頻像僅需要單頻回波就可以分析散射中心的空間位置分布,因此相比于高分辨成像方法,其所需要的散射數據更少。不同類型散射中心的時頻像特征也不同[19]。基于目標勻速轉動的假定條件,在雷達連續觀測獲得回波的時頻像特征中,DSC呈現為豎直亮線,局部型散射中心呈現為正弦曲線(有遮擋時曲線不連續),SSC呈現為非正弦曲線的亮線。這些時頻像特征的差異為散射中心類別以及目標幾何特征的識別提供了理論基礎[20-21]。

本文以錐-柱-臺結構彈頭為例,給出了詳細的散射中心類型以及時頻像特征分析。幾何模型和散射中心分布如圖1(a)所示。彈頭頂部半徑為b0,底座底面半徑為b1,圓柱半徑為b2,尖頂、柱身、底座的高分別為h1、h2、h3,θ為觀測角度。彈頭目標的散射中心包括DSC和LSC兩大類。由于球頂半徑較小,可將該處散射中心視為LSC。底部曲邊緣的散射中心在雷達俯仰觀測面內位置固定,因此這里也可視為LSC。依據幾何結構和散射中心的形成機理可預估出,可能形成的散射中心如圖1(b)所示。

圖1 烈火1幾何結構和散射中心分布Fig.1 Geometry and scattering center distribution of Agni-1

經實際計算發現,LCS2、LSC3幅度很弱,在時頻像中幾乎無顯示,因此在散射中心建模中不予考慮。其他散射中心的數學模型及參數說明如表1所示。

表1 烈火1散射中心的類型、成因和模型表述

表1中,LSC1、LSC4、LSC5的數學模型為

DSC1、DSC2、DSC3、DSC4的數學模型為

式中:L為分布型散射中心的長度參數。

假設目標在XOZ面內勻速轉動,雷達頻率f為3 GHz,觀測角度為θ，θ=0°～180°,極化方式為VV極化。已知彈頭頂部半徑、底座底面半徑、尖頂底面半徑分別為0.15 m、0.5 m、0.4 m,錐體、柱體、錐臺的高分別為1.986 m、1.8 m、0.275 m。基于全波計算的上述頻率、連續觀測下的散射場數據,再采用遺傳算法估計得到散射中心的未知參數[3],全波法與模型仿真結果時頻像的相似度最高為遺傳算法所使用的目標函數。

由全波法計算散射場的時頻像和散射中心模型模擬得到的時頻像如圖2(a)和圖2(b)所示。本文采用的時頻變換方法為重排平滑偽魏格納維爾分布(reassigned smoothed pseudo Wigner-Ville distribution, RSPWVD)法[22]。各類散射中心也在圖2中進行了標注。兩時頻像的相似度為92%,表明散射中心模型仿真精度較高。

時頻曲線的特征由目標的幾何結構決定。對于上述彈頭而言,DSC1所呈現的豎直亮線長度由錐面的母線長度決定;DSC2的豎直亮線長度由柱面的高度決定;DSC3所呈現的豎直亮線長度由錐臺側面的母線長度決定;DSC4所呈現的豎直亮線長度由底面的直徑決定;DSC1和DSC2分布型散射中心出現的角度間隔由錐體的半錐角決定;DSC2和DSC3分布型散射中心出現的角度間隔由錐臺的半錐角決定。基于這些信息，可以構建出彈頭目標的主要幾何外形。

圖2 全波法結果與模型仿真結果對比Fig.2 Comparison of full wave method results and model simulation results

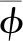
圖3 改變散射中心模型參數后時頻圖像Fig.3 Time frequency image after changing parameters of scattering center model

2 基于CNN的目標識別

在傳統CNN結構中,隨著網絡層的深入,會出現網絡退化的問題,導致訓練集準確率下降[23-24]。在以往的目標屬性分類過程中,特征之間的相關性容易被忽略,降低模型的工作效率,而殘差網絡的優勢正好解決了目標的多屬性識別問題[25-26]。本文選用CNN中的殘差神經網絡(residual neural network, ResNet),該模型網絡深度為18層,其網絡結構設置情況如表2所示。

表2 ResNet結構設置

通過改變散射中心模型參數,獲得2 000幅彈頭目標的時頻圖像。當雷達俯仰角θ相對目標的變化范圍為0°～180°時,結果表明，通過十幾次迭代，就可以獲得很好的識別精度。為了驗證CNN的識別有效性,在3種非理想情況下進行測試,分別為:改變雷達頻率、加入白噪聲、減少觀測角范圍。當改變雷達頻率和加入白噪聲時,彈頭目標的識別效果統計如表3所示。

從表3中的數據可知,在頻率不同的情況下,目標的識別效果幾乎不受影響,因為改變頻率對時頻像特征而言僅為尺度縮放,圖像特征并沒有明顯改變;在散射場數據中加入的白噪聲,在時頻像中體現為斑點噪聲,但信噪比大于10 dB時,并不改變時頻像特征中豎直亮線的長度分布,因此雖然CNN的識別效果會有1%～3%的降低,但就整體而言不會對神經網絡的識別造成過大的干擾。此外,經測試,在測試樣本中加入其他類型目標的時頻像時,網絡的穩定性不受影響。

表3 改變頻率并加入白噪聲后的識別效果

對于上述彈頭目標,完整的時頻像特征需要觀測角度掃描范圍為0°～180°(俯仰角),CNN中卷積運算的目的是提取輸入的不同特征,低層次的卷積層可能只能提取一些低級的特征(如邊緣、線條),深層的網絡才能從低級特征中迭代提取更復雜的特征。因此,本文測試了在不同觀測角度范圍下的識別效果。俯仰角θ從0°～30°到0°～180°依次增大角度范圍,測試識別率結果如圖4所示。在圖4中，數據點從左到右分別代表觀測角度范圍為0°～30°、0°～60°、0°～90°、0°～120°、0°～150°、0°～180°。隨著角度范圍的增大,各目標的識別率均逐步增加,證明CNN的識別有很好的泛用性。

圖4 不同俯仰角角度范圍下的識別率Fig.4 Recognition rate in different pitch angle range of θ

3 基于BPNN的目標幾何參數提取

BPNN預測模型一般采用3層結構,根據網絡的效果來調整輸入層節點、隱含層節點和輸出層節點的個數[27-28]。BPNN算法由數據的前向傳播和誤差的反向傳播兩個部分組成。前向傳播是將輸入層傳入的數據輸送到隱含層進行處理，再傳向輸出層,如果輸出的參數值與實際的參數有偏差,則將偏差沿著網絡進行反向傳播，直至網絡輸出的誤差減少到可以接受的程度,或者進行到預先設定的學習次數[29-30]。

本文預測模型采用的結構如圖5所示。以烈火彈頭目標的時頻像作為網絡輸入,wij為輸入層結點與隱含層結點之間的網絡連接權值,wjk為后兩層結點之間的網絡連接權值,輸出為彈頭目標高度參數h1、h2、h3，以及半徑參數b1、b2。

本文中訓練樣本占總體樣本的90%,剩下的為測試樣本。訓練樣本在網絡經歷不斷的迭代更新,當預測準確率達到設定的精度或學習次數之后停止訓練。最后，將訓練出符合要求的BPNN用于彈頭的幾何參數的預測。本文中目標時頻像的個數即為網絡中的輸入層節點數,幾何參數個數即為網絡中的輸出層節點數。參數預測誤差統計平均結果如表4所示。隨機抽取10個測試樣本,將測試樣本的實際幾何參數與預測參數進行對比,如表5所示。由表5可以看出，預測得出的參數與幾何體實際參數具有很高的一致性。

圖5 BPNN拓撲圖Fig.5 BPNN topology

表4 幾何參數預測誤差統計結果

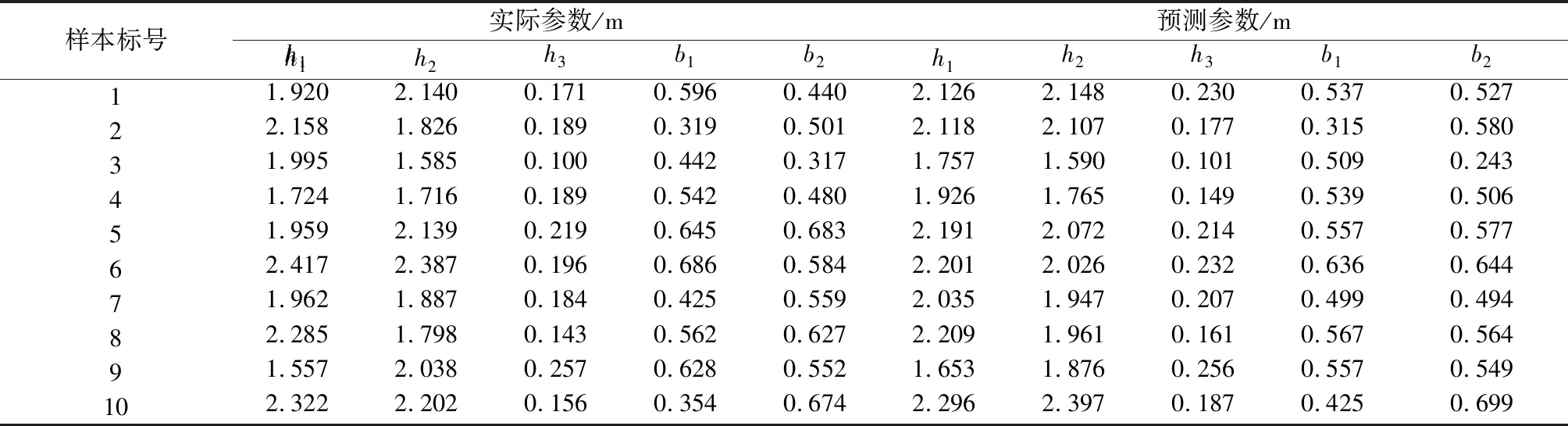
表5 樣本的實際參數與預測參數對比

4 結 論

本文提出了一種基于CNN+BPNN、依據散射中心時頻像特征快速自動識別目標、提取目標幾何參數的方法。在該方法中,采用CNN網絡提取時頻圖像特征用于識別目標類型,之后用BPNN預測得到目標的幾何參數。建立該網絡首先需要大樣本散射場數據庫,然而目標的散射數據庫計算非常耗時,為此提出了利用神經網絡以及散射中心模型快速生成大樣本時頻像的方法。以錐-柱-臺彈頭目標為例,通過數值仿真驗證了該網絡的泛用性,以及幾何參數提取精度。與傳統方法相比,本網絡可實現少量散射數據下的彈頭類的自動化識別和幾何參數提取。該方法也可以推廣應用于幾何結構相似、尺度不同的其他類型目標。