基于Masreliez-Martin的魯棒分數階容積卡爾曼濾波算法及應用

穆 靜, 嚴東升, 蔡遠利, 王長元

(1. 西安工業大學計算機科學與工程學院, 陜西 西安 710021; 2. 北京航天長征飛行器研究所,北京 100076; 3. 西安交通大學電子與信息學部, 陜西 西安 710049)

0 引 言

國內外學者研究了許多非線性系統的免微分濾波算法,如無跡卡爾曼濾波(unscented Kalman filter, UKF)采用了一組確定Sigma點的Unscented變換[1]、離差差分卡爾曼濾波算法(divided difference Kalman filter, DDKF)利用斯特林插值公式計算均值和協方差[2]、容積卡爾曼濾波(cubature Kalman filter, CKF)利用球面徑向容積準則逼近狀態后驗分布[3]。CKF克服了UKF和DDKF在高維非線性狀態估計中的缺點,同時能夠具有更高的濾波精度,獲得了廣泛的應用[4-5]。

在實際應用中,被估計系統的函數模型和噪聲統計特性常常不能夠準確獲得, 直接采用上述的免微分濾波算法會導致估計精度大幅度降低。為了提高估計精度,許多學者提出了魯棒濾波算法。文獻[6]提出了基于非高斯量測噪聲下的Huber自適應UKF算法,并討論了關鍵參數對算法的影響。文獻[7]提出了基于Huber方法的高階容積卡爾曼跟蹤算法,使用統計線性回歸模型近似非線性量測模型的基礎上, 利用Huber M估計算法實現狀態的量測更新,結合高階容積準則構成了所提的算法,同時分析了Huber代價函數的調節因子對算法跟蹤性能的影響。文獻[8]研究了基于魯棒CKF的自適應目標跟蹤算法,借鑒Huber等價權函數的思想, 構造了基于平方根平滑逼近函數的修正因子以抑制觀測野值的影響, 并結合CKF器求解框架推導出該算法。文獻[9]討論了基于Huber的魯棒廣義高階CKF算法,采用 Huber方法處理觀測量,進行標準的廣義CKF量測更新,從而實現算法的魯棒化,充分利用了容積變換的優勢,無需通過統計線性回歸模型對系統的非線性量測模型進行近似。文獻[10]提出了非高斯噪聲下的非線性隨機系統的基于Masreliez-Martin(M-M)方法的魯棒擴展卡爾曼濾波算法。進一步的,文獻[11]提出了一種基于M-M方法的自適應和魯棒UKF算法,可以在存在未知過程噪聲和測量噪聲協方差矩陣的情況下提供可靠的狀態估計。

另一方面,實際應用中對有些系統的建模本身需要用分數階來描述,而有些系統使用分數階模型可以更好建模所研究的系統,因此分數階系統成為了越來越多學者的研究熱點。針對高斯環境下的離散分數階隨機系統,文獻[12]提出了分數階(擴展)卡爾曼濾波并應用到目標的狀態估計。文獻[13]以概率論為基礎,從分數階的非線性動態系統模型出發,推導了分數階UKF(fractional UKF, FUKF),并應用于再入飛行器的狀態估計上。文獻[14]使用統計線性方法和容積變換,提出了分數階CKF(fractional CKF, FCKF)算法,相比于分數階擴展卡爾曼濾波算法,仿真實驗證明了該算法的有效性和優越性。文獻[15]提出了分數階插值CKF(fractional interpolatory CKF, FICKF)算法,并討論了FUKF和FCKF是FICKF算法的兩種特殊形式。文獻[16]提出了未知先驗信息狀態下的分數階中心差分濾波算法,并且,從貝葉斯濾波的視角分析了分數階非線性系統的狀態估計問題[17]。而文獻[18-19]分別提出了基于新息的自適應分數階卡爾曼濾波算法和基于模糊邏輯方法的FUKF算法。在高斯分布噪聲環境下,上述方法都獲得了有益的結果。進一步的,一些學者研究了某些特殊噪聲下分數階系統的狀態估計問題[20-21]。

針對連續分數階系統的狀態估計問題,文獻[22-23]討論了基于Tustin 生成函數的分數階卡爾曼濾波器設計方法, 解決了相互關聯的分數階有色過程噪聲和分數階有色測量噪聲下的連續時間線性分數階系統的狀態估計問題。文獻[24]討論了連續分數階系統的FUKF算法,相比于擴展卡爾曼濾波算法,提出的算法具有較準確的估計效果。文獻[25-26]討論了使用Tustin生成函數和分數階導數平均值方法,提出了針對具有相關和非相關過程噪聲和量測噪聲的連續分數階系統下的分數階擴展卡爾曼濾波算法和FUKF算法。進一步,文獻[27-28]研究了針對非線性連續時間系統的CKF算法的初始參數問題和未知參數和分數階問題。

本文針對具有非高斯量測噪聲的分數階非線性系統的狀態估計問題進行研究,以分數階動態隨機系統為模型,結合三階容積原則和M-M方法,改變其量測更新過程,建立基于M-M方法的魯棒分數階CKF算法(M-M based robust factional CKF, MMFCKF)。由于分數階微積分的固有特性,FCKF器具有“記憶”特性,其下一時刻的估計值不僅與系統當前時刻的狀態有關,還依賴于當前時刻之前的系統的運行情況。在觀測噪聲污染率較高的情況下能夠有效地抑制污染噪聲的影響, 具有較強抗差能力。最后,將MMFCKF算法應用到再入目標的狀態估計中,同時分析不同程度的污染噪聲對算法性能的影響。仿真實驗表明,MMFCKF優于FUKF和FCKF,同時驗證了新算法的有效性和魯棒性。

1 分數階非線性系統和容積原則

1.1 分數階非線性隨機系統

分數階微積分是非整數階微積分或者是任意階微積分,是整數階微積分的推廣[29]。自從萊布尼茲等人提出后,數學家們從不同角度給出了分數階微積分不同的定義, 每個定義的合理性和科學性在實踐中得到了廣泛檢驗。為了易于處理狀態估計問題,本文使用Grünwald-Letnikov定義[12]:

(1)

(2)

使用式(1),非高斯量測噪聲的分數階非線性離散隨機系統[12,15]可表示為

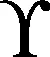
(3)

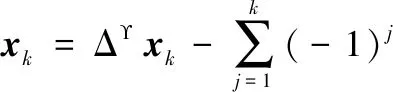
(4)

zk=h(xk)+ek

(5)

(6)

式中:xk∈Rnx為狀態向量;f(·)和h(·)為非線性狀態方程和量測方程。式(4)計算機實現時需要使用有限個過去狀態(L),即xk-L+1,xk-L+2,…,xk。zk∈Rm是量測值,α1,α2,…,αn,i∈{1,2,…,n}是系統的分數階;wk是均值為零和方差為Qk的高斯白噪聲;ek是非高斯的量測噪聲,其概率分布函數如下:

p(ek)=(1-)pN(ek)+q(ek)

(7)

式中:pN(ek)服從高斯分布函數N(ek,0,R1,k),稱為標稱量測噪聲,q(ek)服從N(ek,0,R2,k)是污染噪聲,參數∈(0,1)代表了污染噪聲對系統的污染度。記是k時刻的量測集合。

1.2 三階容積原則

在貝葉斯框架下,非線性濾波問題可歸結為以高斯概率分布為權值的非線性函數的積分問題[3]。首先考慮如下標準正態分布的積分問題:

(8)

式中:Integral(g)為所求積分;x為濾波估計狀態向量,x∈Rnx,Rnx為積分域;g(x)為非線性函數; N(x;0,I)為標準正態分布,I為單位矩陣。使用基于三階容積原則的數值積分方法可得式(8)的近似解[3]:

(9)

式中:ξi為基本容積點;ωi為容積點對應的權值。ξi和ωi的取值分別為

(10)

實際應用中,需要求解權值為非標準正態分布的非線性函數的積分。對于一個非標準正態分布函數N(x;μ,Σ),μ為均值,Σ為協方差矩陣,那么:

(11)

(12)

利用式(9),可得到式(12)的近似解:

(13)

2 MMFCKF方法

本文提出的算法使用文獻[12]中的兩個假設,其合理性是顯然的[15-16]。

2.1 時間更新

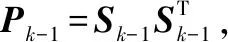
(14)

(15)

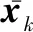
(16)

(17)

已知噪聲wk是均值為零的白噪聲,在假設1下,可得式(16)的第2項和第3項:

(18)

(19)

將式(17)～式(19)代入式(16),可得狀態預測為

(20)

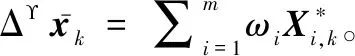
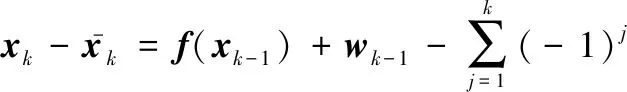
(21)

(22)

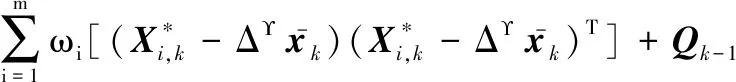
(23)

(24)

(25)

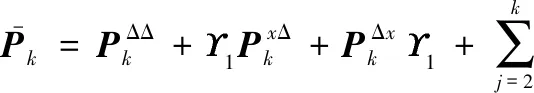
(26)

2.2 量測更新

(1) 計算容積點

(27)

(2) 計算通過非線性量測方程傳播的容積點

γj,k=h(Xj,k)

(28)

(3) 計算量測預測、新息方差和協方差估計

(29)

(30)

(31)

(4) 使用M-M方法,計算狀態估計和協方差

(32)

(33)

其中,增益Kk和vk定義如下:

(34)

(35)

(36)

(37)

(38)

式中:L為常數。

3 仿真實驗

為了驗證本文所提的MMFCKF的有效性,將算法應用到再入彈道目標(re-entry ballistic target, RBT)跟蹤問題[30-31]中的狀態估計,并與FUKF和FCKF算法對比,進一步分析量測污染噪聲因子對算法的性能影響。

3.1 再入目標跟蹤模型

圖1描繪了再入彈道目標在一維坐標系下雷達對再入彈道目標的跟蹤過程。彈體垂直下落,雷達跟蹤彈體并測量了彈體和雷達之間的距離。

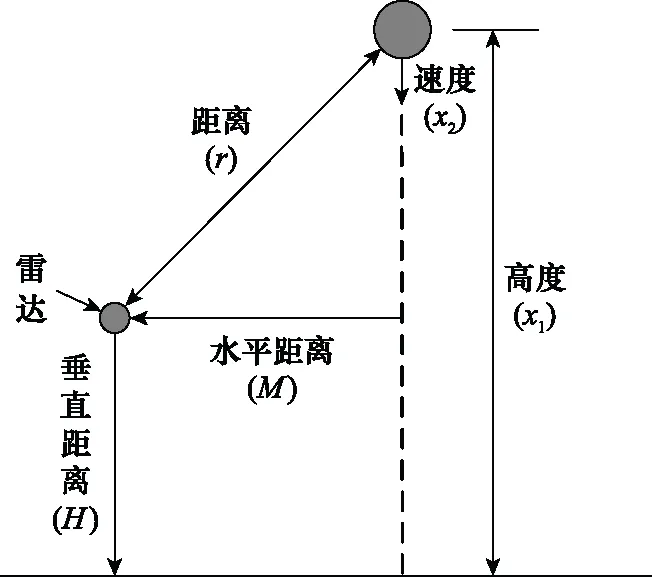
圖1 RBT和雷達的幾何關系Fig.1 Geometry of RBT and radar

根據內大氣階段的阻力,RBT的狀態方程[30-31]可以建模為

(39)

式中:狀態值x=[x1(t),x2(t),x3(t)]T分別表示垂直落體的高度、向下速度和彈道系數,這里取彈道系數為β=5×10-5。式(39)是連續時間模型,對應采樣時間T的離散化模型f(xk-1)為

x1(k)=x1(k-1)-tx2(k-1)+w1,k-1

(40)

x2(k)=x2(k-1)-te-βx1(k-1)x2(k-1)2x3(k-1)+w2,k-1

(41)

x3(k)=x3(k-1)+w3,k-1

(42)

這里假設wk=[w1,k,w2,k,w3,k]T是均值為零和協方差為Qk的高斯噪聲。使用式(40)～式(42)直接表示彈道目標的運動模型時,會損失掉有用的狀態信息,使用分數階系統描述系統能獲得更為豐富的信息[32]。定義f(xk)=[x1(k),x2(k),x3(k)]T,再入目標的分數階狀態方程可表示為式(4)的形式。

根據RBT與雷達的幾何關系,雷達以采樣時間間隔t測量與再入目標的距離r,再入目標在k時刻相對雷達的距離rk由測量方程給出:

(43)

在實際應用中,ek為非高斯噪聲,往往伴隨高尾分布而出現,獨立于狀態噪聲wk,表達式如式(7)所示。M為雷達到落體路徑的最短水平距離,H為雷達距離地面的高度。本文取M=100 000 ft,H=100 000 ft[30-31]。

蒙特卡羅仿真實驗中,使用均方根誤差(root mean square error, RMSE)驗證算法的有效性。k時刻的位置RMSE定義為

(44)

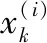
為了進一步分析算法的有效性,本文使用累加RMSE(accumulated RMSE, ARMSE),位置ARMSE定義為

(45)

式中:N為測量數據點個數。用類似的方法定義速度和彈道系數公式的ARMSE。仿真實驗中蒙特卡羅次數為100次,使用式(44)和式(45)計算RMSE和ARMSE。為了更清晰地顯示各種算法的結果,后文仿真結果圖中y軸上使用對數坐標。

3.2 仿真實驗分析

3.2.1 MMFCKF與FUKF, FCKF算法性能比較

標稱測量噪聲協方差選擇R1,k=1002ft2,污染測量噪聲協方差選取R2,k=5002ft2。圖2～圖4分別給出了污染噪聲因子=0.5的MMFEKF,FUKF和FCKF算法的位置、速度和彈道系數的均方根誤差。

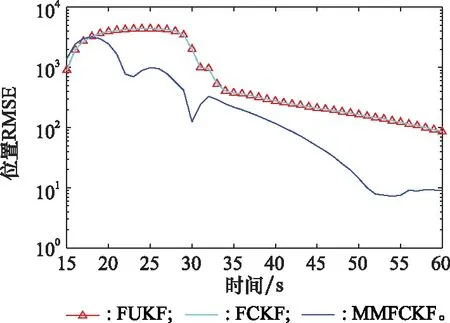
圖2 目標位置估計的RMSEFig.2 RMSE of target position estimation

從圖2中可以看出,相比于FUKF和FCKF,MMFCKF的位置狀態估計RMSE大幅度下降,濾波器收斂速度較快。圖3和圖4顯示了MMFCKF的速度和彈道系數的RMSE從32 s時開始大幅下降,說明MMFCKF對于狀態突變具有較強的跟蹤能力,這是由于當存在目標狀態突變時,雖然系統模型失準,M-M方法能根據測量殘差的變化修正一步預測協方差陣,進而在線實時調整增益矩陣Kk,這樣就能充分提取殘差序列中的有效信息,使跟蹤精度有了明顯提高。同時,濾波收斂速度較快,說明MMFCKF對于狀態突變具有較強的跟蹤能力。

圖3 目標速度估計的RMSEFig.3 RMSEs of target velocity estimation

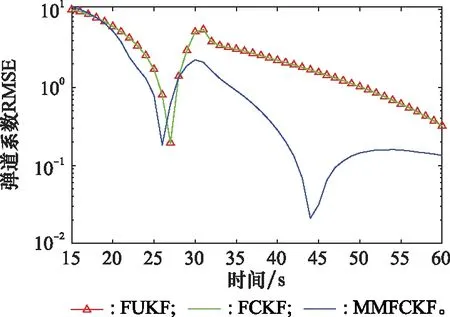
圖4 目標彈道系數估計的RMSEFig.4 RMSEs of target ballistic coefficient

使用ARMSE進一步對提出的算法進行性能分析,3種算法的ARMSE的柱狀圖如圖5所示。圖5顯示,相比于FUKF和FCKF算法,MMFCKF算法的位置、速度和彈道系數的ARMSE大幅度減小。相比于FUKF 和FCKF 算法,MMFCKF算法的位置ARMSE分別降低了35.47%和35.22%,速度ARMSE分別降低了20.98%和20.93%,彈道系數ARMSE分別降低了6.23%和6.06%,再次表明了MMFCKF 具有很強的跟蹤能力。從圖2～圖5也表明了FUKF 和FCKF 算法對目標的跟蹤性能相似。

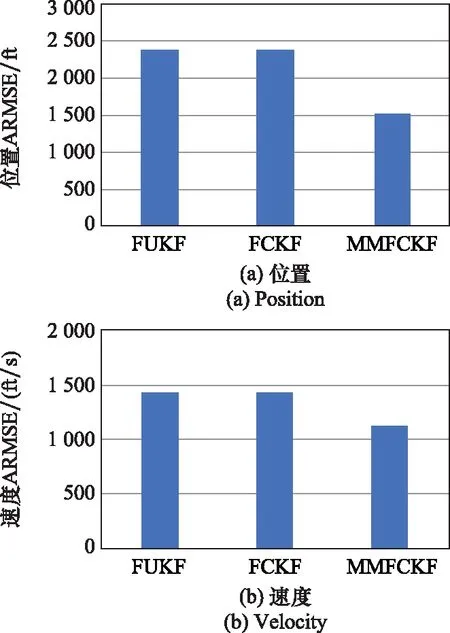
圖5 不同算法的目標ARMSEFig.5 Target ARMSEs of different algorithms

3.2.2 噪聲污染因子對算法性能的影響

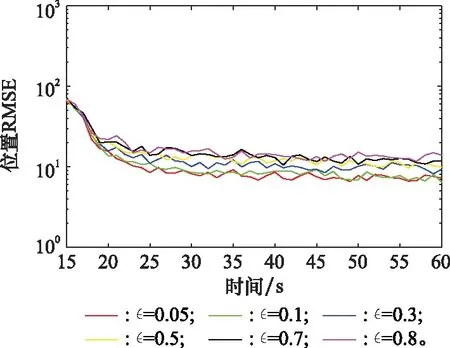
圖6 不同的MMFCKF的目標位置RMSEFig.6 Target position RMSEs for MMFCKF with various

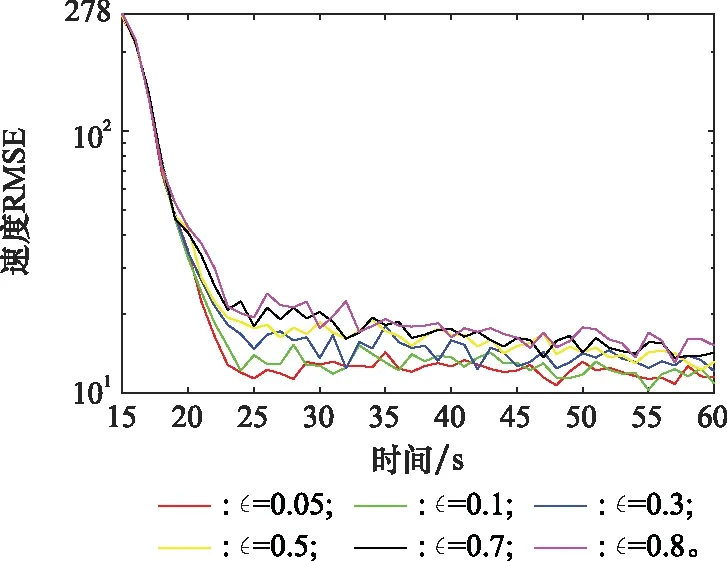
圖7 不同的MMFCKF的目標速度RMSEFig.7 Target velocity RMSEs for MMFCKF with various

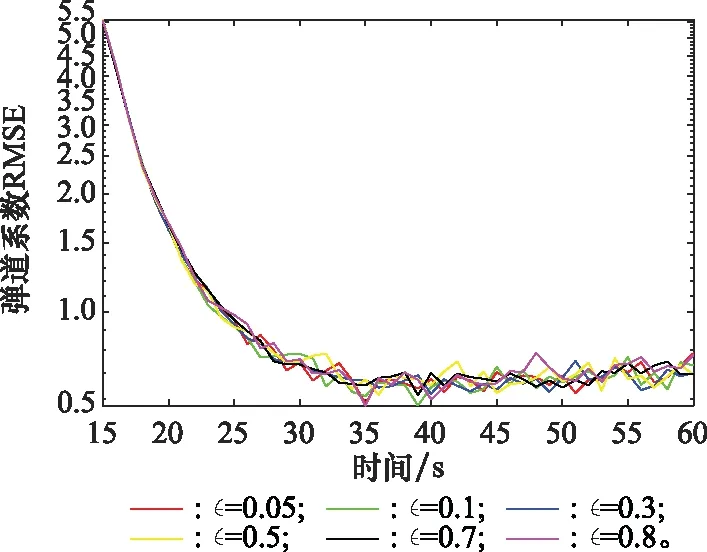
圖8 不同的MMFCKF的目標彈道系數RMSEFig.8 Target ballistic coefficient RMSEs for MMFCKF with various

從圖6和圖7可以看出,隨著污染噪聲因子增加,MMFCKF算法的位置和速度RMSE稍微在增加,但增加時相對穩定,對于彈道系數的RMSE并沒有隨著污染噪聲因子的增加出現明顯的增加,意味著MMFCKF算法可以有效抑制污染的測量噪聲,M-M方法可以有效抑制污染噪聲,大大的提高了估計精度,體現了MMFCKF算法在污染噪聲環境下對目標跟蹤的優越性。

4 結 論

本文研究了分數階離散非線性系統狀態估計問題,利用M-M方法對量測更新過程進行改進,構造了基于M-M方法的魯棒FCKF器。該算法充分使用了量測數據的有用信息,抑制了量測噪聲中的污染噪聲對算法性能的影響,具有很好的穩定性。大量仿真結果表明,與FUKF算法、FCKF算法相比,MMFCKF算法能夠很好地抑制污染噪聲,具有更好的性能。最后,分析了不同程度的量測污染噪聲對算法的性能影響,進一步驗證了算法具有較高的魯棒性。