基于隨機森林權重補償的無人機高精度定位算法

方 坤, 李曉輝, 樊 韜

(1. 西安電子科技大學綜合業務網國家重點實驗室, 陜西 西安 710071;2. 國家計算機網絡與信息安全管理中心河南分中心, 河南 鄭州 450000)

0 引 言

無人機(unmanned aerial vehicle, UAV)憑借其運動靈活、可操作性大、體積小等特性在戶外環境中(警務、交通管制和農場管理)有了廣泛的應用,但對UAV的監管也越來越困難,因此UAV定位成為近年來的熱門研究課題[1-2]。在利用移動通信基站對UAV進行定位時,由于UAV體反射信號微弱、地面障礙物所引起的多徑噪聲干擾以及移動通信基站設備信號功率較低等因素導致了難以對UAV進行實時無源定位[3-4]。

對UAV進行無源定位主要分為基于到達角度、圖像識別和到達時間差三個方向[4-12]。Liu等[4]和Kim等[5]分別提出了非線性卡爾曼濾波算法對UAV反射信號進行載波相位處理,得到位置信息。但是在估計UAV的到達角度時,對于UAV過小所導致的角度信息誤差較大問題都沒有很好的解決辦法。Stojcsics等[6]提出了一種熱成像視覺定位算法。通過熱成像檢測UAV與環境的溫度差,利用圖像識別對目標進行定位。這種圖像識別算法具有很高的UAV定位精度,但對硬件設備要求過高。Koivisto等[7]、Carrillo等[8]和Chen等[9]分別提出了改進的三邊定位算法,通過獲取多個基站與UAV的距離信息,建立球體,以球體交點作為目標坐標。但是,對于三邊定位算法魯棒性較差的問題都沒有很好地進行解決,均需要多次平滑誤差。Su等[10]提出了一種基于非線性補償的Pilsbon算法,針對UAV信號淹沒在噪聲中的問題,通過改變迭代最小二乘法的線性度,將UAV定位信號的非線性共振峰效應轉化為線性,進而估計目標坐標。然而,該模型只適用于特殊的環境空間,對接收基站的位置選擇有較高的要求。文獻[11]提出一種基于信號相似度和空間位置的K近鄰(K-nearest neighbor, KNN)算法。通過平衡信道狀態信息差和信號傳播距離來獲得UAV定位信息,但其僅適用于距離較小的場景下對于UAV信號進行重構。文獻[12]提出一種基于支持向量機(support vector machine, SVM)的UAV定位算法。通過UAV定位信號的功率與相位信息映射高維空間定位,但其對UAV定位數據要求過高,且計算復雜度較高。文獻[13,14]提出了基于Chan-Taylor算法的UAV定位算法,將定位結果作為泰勒算法迭代的初值,停止迭代,直到誤差低于閾值,最后輸出定位結果。

本文提出了一種基于隨機森林權重補償的高精度定位算法,用于對三維空間中單一UAV進行高精度定位。根據Chan-Taylor算法的誤差變換和隨機森林模型特征提取,推導了距離權重補償的數值表達式。該算法主要解決了UAV定位過程中多徑噪聲所導致的定位誤差較大問題。在多個定位接收基站的情況下,該模型利用機器學習中計算復雜度較低的隨機森林對UAV反射信號數據進行特征提取,結合Chan-Taylor方法,將定位信號多徑噪聲轉化為高斯分布并進行距離誤差補償。在得到定位結果后,對定位結果進行誤差標定并校正設備誤差,提高定位精度。該算法實現了對UAV的高精度定位且具有實時性和魯棒性。

1 UAV無源定位系統

在室外較為空曠的環境下,三維定位利用現有移動通信基站廣播信號對UAV進行無源定位[15]，系統模型如圖1所示。UAV本身不與基站進行信號交互,僅利用移動通信廣播信號作為定位信號經UAV反射到接收基站,通過提取信號特征,實現UAV定位。接收信號主要由UAV反射波和噪聲組成。

(1)

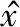
在對UAV定位信號傳播過程中的信號時延與相位偏移分析后,式(1)可以細化為

(2)

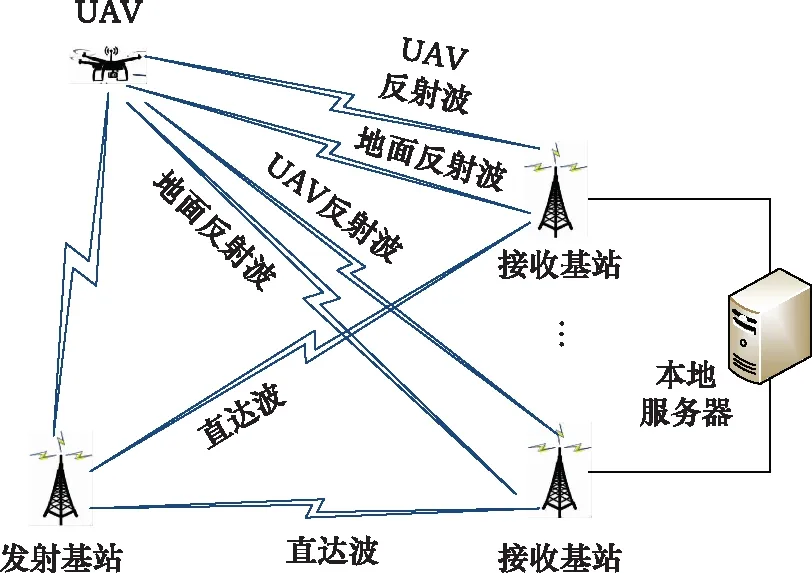
圖1 系統模型Fig.1 System model

隨機森林模型通過對大量的UAV定位數據進行分析和處理,提取出UAV信號x(t)的微弱特征并進行定位。在對UAV信號進行時差估計后得到UAV距離信息xd,因此隨機森林模型[16]可建立為

h(xd,θk)=θ0+θ1x1,d+θ2x2,d+θ3x3,d+…+θkxk,d
s.t.k=1,2,…,Ndata;d=1,2,…,Ndata

(3)

式中：θk表示從UAV反射信號特征中提取的第k組數據的分類因子,Ndata為數據集的個數。θk的選擇基于Gi(Di):

(4)

式中：pi表示第i種定位數據樣本特征區間占整個定位信號數據集該類特征區間的比例；m表示從定位數據中提取的UAV信號特征值，即均值、方差、最小值、最大值、偏度、峰均比、均方根延遲擴展和中位數。通過這些特征的細微變化和大量數據的驗證,建立隨機森林模型,得到距離誤差補償參數,從而獲取UAV的坐標信息。

(5)

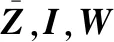
本文的創新之處在于采用隨機森林算法提取定位信息中的數據特征,并對定位數據進行分類,實現多徑噪聲情況下對UAV反射的微小信號提取。根據分類結果定義權重矩陣W,對UAV高度數據進行有效修正。此外,利用誤差標定來校正設備誤差,提高定位精度。

2 隨機森林權重補償定位算法

在多個定位接收基站對檢測空間范圍內的單一UAV進行定位時,隨機森林權值補償算法通過將隨機噪聲誤差轉化為高斯分布并進行去噪后,構建隨機森林模型進行定位數據特征提取,獲取定位權重矩陣。此外,利用標定UAV對定位結果進行誤差標定,降低設備誤差,提高定位精度。

2.1 隨機森林定位

隨機森林算法具有集成度高、建模速度與數據處理快等優點,對于UAV反射信號特征的提取具有良好的適用性。在建立隨機森林模型時,通過KNN來解決如何在短時間內獲取大量數據用以模型構建,保證模型實時性。此外,Chan-Taylor算法被用于將隨機信號噪聲轉化為高斯分布,降低數據噪聲,提高最終定位精度。

KNN算法定義如下:

(6)

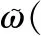
在獲得大量初始定位數據后,為了解決UAV定位數據中信號噪聲過大問題,便于后續特征提取,采用Chan-Taylor算法將隨機信號多徑噪聲轉化為高斯分布[19]。

(7)

式中：Φl是Chan-Taylor算法中用于估計第l組訓練數據組距離的權重(Φl取單位矩陣)；yl是第l組距離估計的輸出；xl是第l組的輸入數據；β是該組數據的特征系數,一般取1；nl是該組數據中UAV信號噪聲。

對定位數據中的噪聲進行處理后,根據定位數據的最小二乘誤差,選擇與數據特征(均值、方差、最小值、最大值、偏度、峰均比、均方根延遲擴展和中位數)相關的最優閾值,并對決策樹節點(單棵決策數特征閾值)進行剪枝,去掉部分決策樹的無用閾值分類數值,提高模型的泛化能力。此外,對決策樹節點進行剪枝后,可以避免無用數據處理,降低計算復雜度[20,21]。

(8)

式中：V(k)表示所選決策樹參數評價得分；Mu表示使用第u個參數后得到的定位結果精度；kc表示數據集的個數。

在選擇決策樹節點的過程中,Gl(S)用來表示當前定位數據與所需要分類的數據集閾值特征不一致的概率,定義如下：

(9)

式中：Gisplit(S)表示節點的劃分依據,通過對Gisplit(S)交叉驗證可以自適應地選擇θk;Sl表示數據特征中大于訓練集所選數據特征θk的數據集個數(這里認為均值、偏度、峰均比、均方根延遲擴展、極值5個數據特征中有3個大于訓練集所選數據特征即可);S為數據集總數;Gl為隨機森林訓練過程中所使用的基尼指數[22],初始值取0.2,由小樣本數據實際測試得到,在數據樣本增大后,依據式(10)確定最優值。

(10)

式中：pl,f表示位置估計值定位誤差小于期望精度(初始期望精度為小樣本數據可以得到的最優UAV定位精度,當后續連續定位時,以訓練集能達到的最優精度與當前期望精度的中間值作為新的期望精度進行更替)的位置數據樣本占總數據集的比例；Dl是第l組數據集；m代表從定位數據中提取的UAV信號特征數量。

隨機森林建立過程如圖2所示。

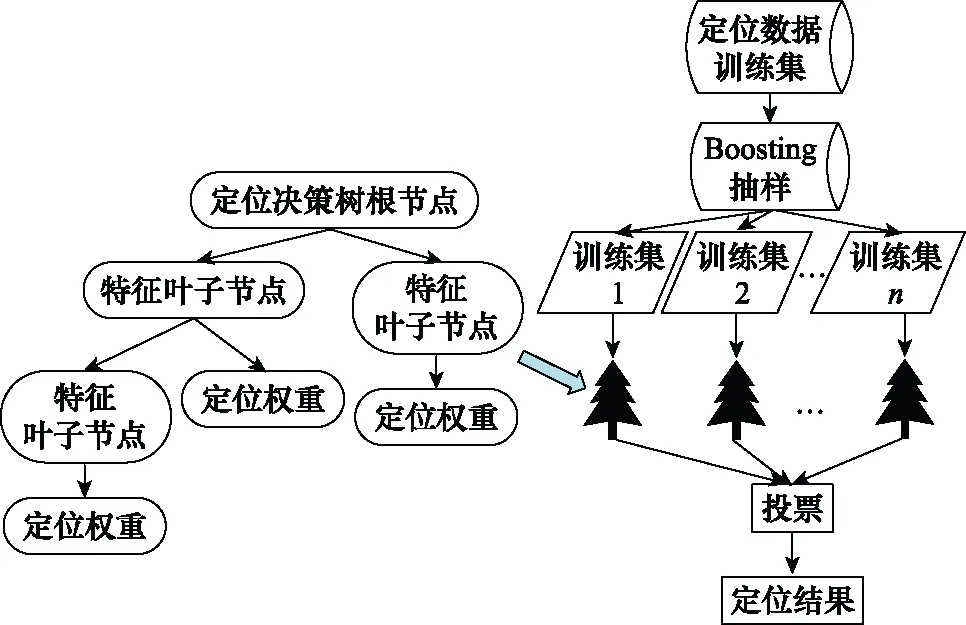
圖2 隨機森林建立過程Fig.2 Random forest establishment process

在對隨機森林進行估計后,利用二元混淆矩陣對模型進行評價[16]，如表1所示。

表1 二元混淆矩陣

表1中TP、FN、FP、TN分別表示正確分類且被正確判斷、正確分類但被錯誤判斷、錯誤分類但被正確判斷、錯誤分類且被錯誤判斷。

相對比傳統的評價矩陣只以l個數據集的TP作為評價矩陣的主對角線,本文通過分別加入FP和FN作為次對角線,使得第i組訓練數據和第(N-l)組訓練數據同時對結果進行修正。評價矩陣如下：

(11)

使用權重補償矩陣P與xd相乘后,得到校正的距離Rl,進一步得到Fvalue作為對UAV隨機森林定位模型的評價

(12)

Si代表第i種特征下的正確率與召回率值矩陣。

在對模型進行權值補償后,進行目標位置信息獲取。首先得到距離校正參數

fi, j=1-μ(ri, j-Ri)

(13)

式中：fi, j是距離修正系數。在定位精度為Facc的情況下,設置位置誤差的迭代參數μ為Facc/2,便于歸一化處理,降低計算復雜度。ri, j是第i個接收基站和第j個中心基站之間的距離。Ri是利用隨機森林模型對目標到接收基站的距離校正后的數據。距離校正后的權重矩陣W′定義為

(14)

將更新后的迭代矩陣W′代入式(5),估計出目標UAV的三維坐標。

2.2 誤差標定

在檢測空間設置一個已知UAV位置的標定目標,獲取UAV與各個基站之間的距離(the distance between the UAV and each base station, BSD)和UAV運動速度(the calibration UAV moving rate, CUV)測量值來估計在定位過程中由發射基站和接收基站引起的微小定位誤差[23]。

當檢測到UAV進入監控區域后,校準UAV開始在檢測區域飛行,通過BSD和CUV信息定位待測UAV。對已知坐標UAV進行定位,得到當前設備的定位誤差[24](基站坐標誤差和距離估計中的小數時延估計誤差)。如圖3所示。

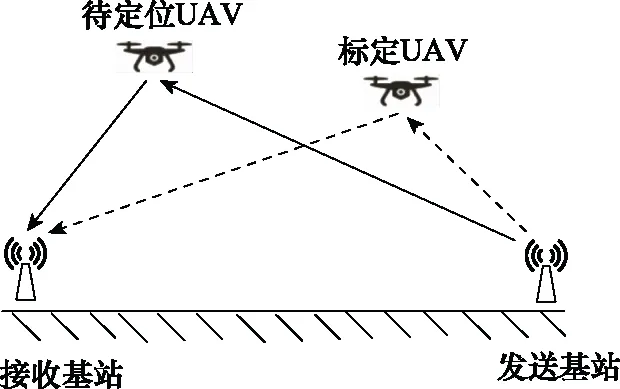
圖3 誤差標定Fig.3 Error calibration

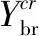
(15)

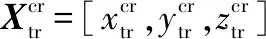
(16)

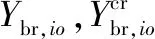
(17)

(18)

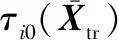
Hα=B+E

(19)

式中:H是時差估計梯度矩陣;α是UAV距離差分矩陣;B是UAV時差矩陣;E是UAV時差估計誤差。

(20)

式(21)可由式(17)得

(21)

將式(20)與式(21)結合,得到

(22)

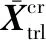
3 系統仿真

在仿真中,6個信號接收基站均勻分布在半徑1 000 m的圓周上,一個發射站分布在圓中心。待定位目標是反射面小于0.02 m2的小型UAV,并依據UAV反射信號模型,增加與反射面大小相對應的反射信號功率衰減[27-30]。信號發射基站坐標為(0,0,10)。本文所提算法在Win10系統上,利用Python3.7.9進行仿真。仿真參數見表2。

表2 仿真參數

在表2中所示參數下建立隨機森林模型。得到了隨機森林定位模型的評價結果，如表3所示。

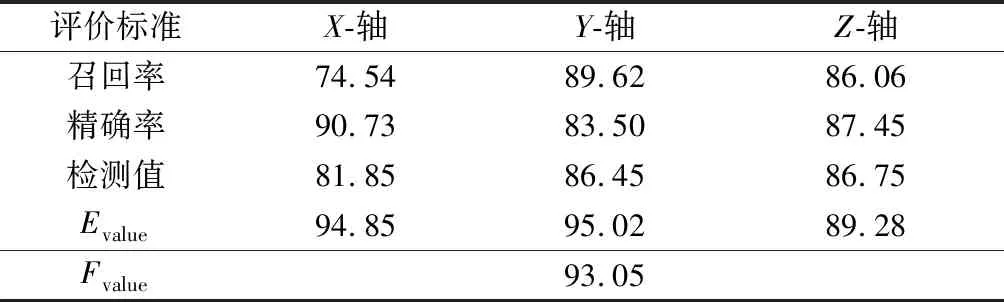
表3 目標坐標定位決策樹的精度分析

其中召回率是正確檢索到的結果占所有結果的比例,精確率是正確檢索到的結果與所有實際檢索到的結果的比例。檢驗值代表隨機森林模型在各坐標軸上的評價得分,用來衡量模型是否與實際相符。Evalue代表隨機森林模型在每個坐標軸上的位置估計的準確率。根據表3中的結果,模型最終的評價結果Fvalue可以達到93.05%。

考慮到UAV本身具有的移動速度慢的特點,仿真將對同一位置固定點進行多次重復定位,而單次定位所花費的時間具有偶然性且數值過小,并且該定位時間內,由于定位過程中UAV運動造成的誤差轉化為UAV運動的距離時,數值過小,故而本文通過對同一個點(200,200,200)處固定位置不變的UAV進行相同參數情況下的多次重復定位后,得到程序的不同算法,同樣多次定位累計運行時間,并進行對比,對本文所提算法與其他算法進行復雜度對比。結果如表4所示。

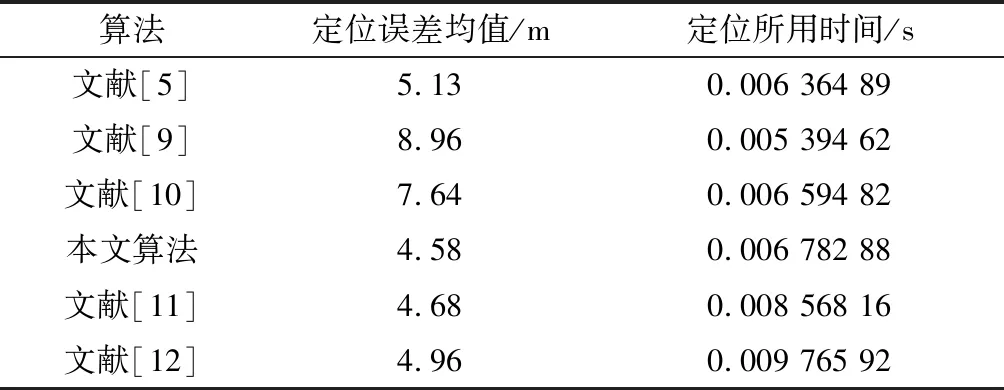
表4 算法運行時間比較

在表4中的定位算法結果數據里,UAV定位時的誤差分為兩部分:UAV固定位置時,算法定位產生的誤差;算法定位時間花費過程中,UAV在此期間運動的距離所導致的誤差。而其中,由于定位時間短以及UAV運動緩慢,定位誤差主要是由UAV固定位置時,算法定位產生的誤差這部分構成。定位誤差均值不同是由算法差異所導致的,而定位所用時間只表示不同算法對同一坐標處的UAV進行同樣次數的定位所用時間。由表4可知,本文算法與文獻[5]、文獻[9]和文獻[10]等非機器學習算法相對比,定位誤差有明顯降低,并且定位所用時間相差較小。本文算法與文獻[11]中KNN算法與文獻[12]中SVM算法這兩種常用的機器學習算法進行計算復雜度對比,機器學習定位誤差相近,但本文所提算法的計算復雜度有明顯優勢,這一點在對運動UAV進行連續定位時,可以明顯降低最終定位誤差。

通過Fvalue對距離數據誤差進行了補償。比較了隨機森林模型在視距(line of sight, LOS)條件下和非LOS(non-LOS, NLOS)條件下與現有的其他定位算法進行了比較。

如圖4所示,本文的算法在LOS和NLOS下與現有的一些算法進行了仿真比較。隨著距離的增加,相應地增加了噪聲誤差。從總體趨勢來看,該方法和其他方法的定位誤差隨著噪聲的增大而增大。但與無跡卡爾曼濾波算法[5]、三邊定位方法[9]和非線性補償Pilsbon算法[10]相比,模型的定位精度有所提高。定位的均方根誤差(root mean square error, RMSE)明顯優于其他算法。

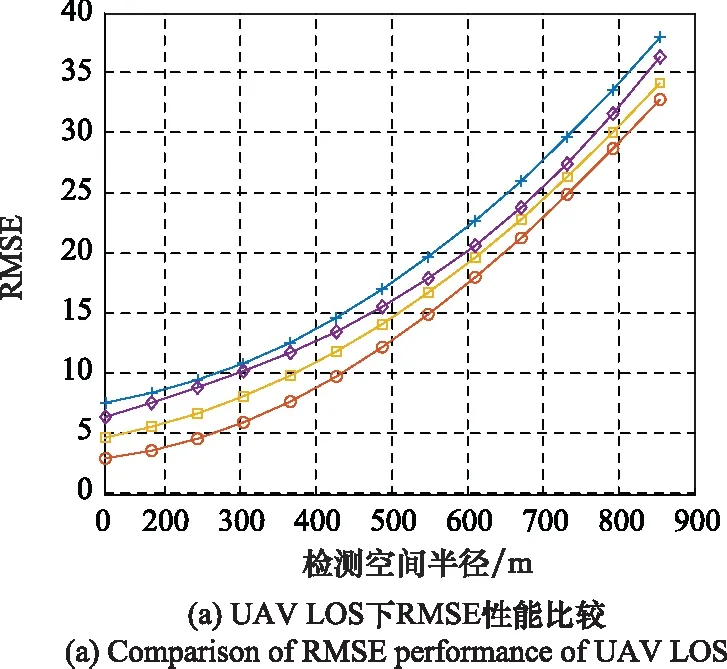
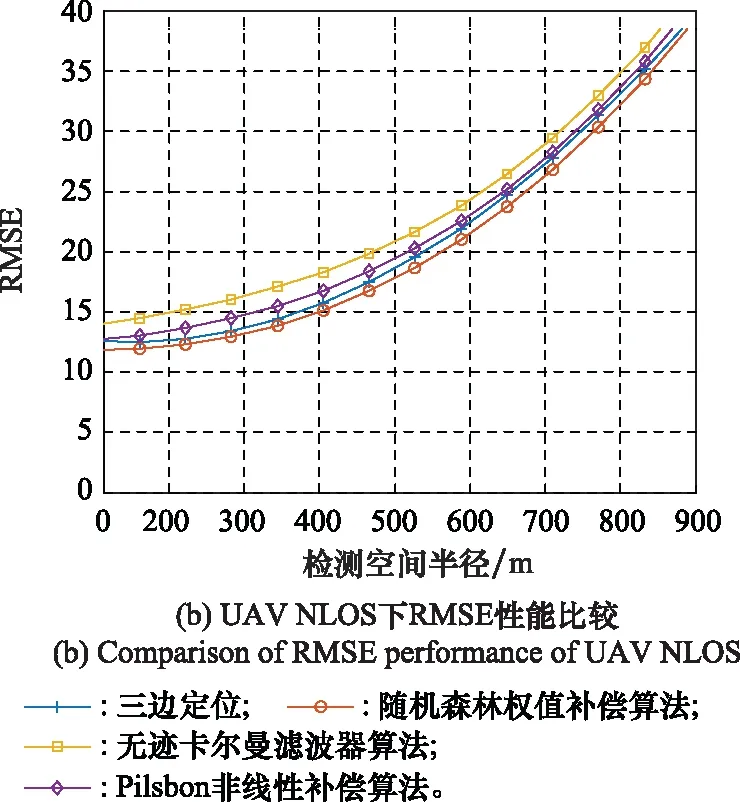
圖4 UAV定位性能比較Fig.4 Comparison of UAV positioning performance

對不同運動速度的UAV進行定位,定位結果如圖5所示。

圖5 UAV速度變化對定位結果影響Fig.5 Influence of UAV speed change on positioning result

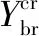
在直徑300 m的探測空間內,隨機生成41個目標點并進行定位，如圖6所示。

在300 m的探測空間范圍內,隨機生成并定位了41個目標點。藍色方形是實際的目標點,紅色圓形是估計的坐標點。從仿真結果可以得出,該定位算法可以有效地定位目標。

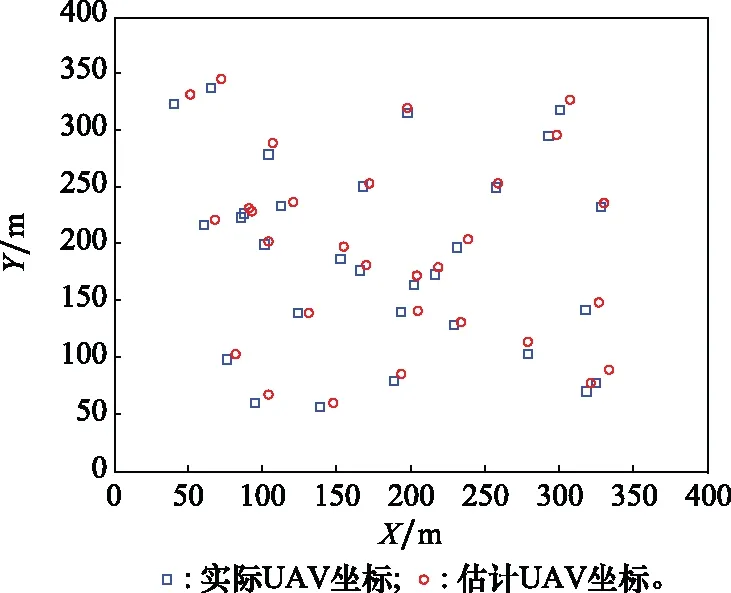
圖6 空間隨機目標定位檢測Fig.6 Spatial random target location and detection

通過改變高度和水平坐標來估計檢測空間中的小目標,并獲得圖7所示的仿真結果。部分估計結果數據如表5所示。

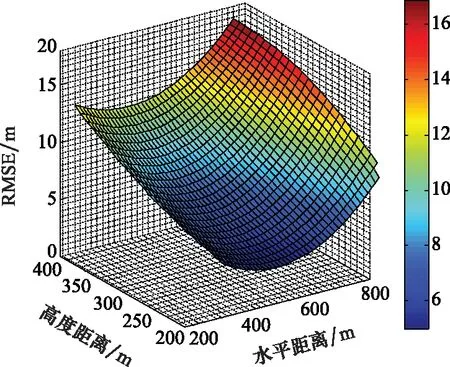
圖7 UAV在三維空間中的定位效果Fig.7 Positioning effect of UAV in three-dimensional space

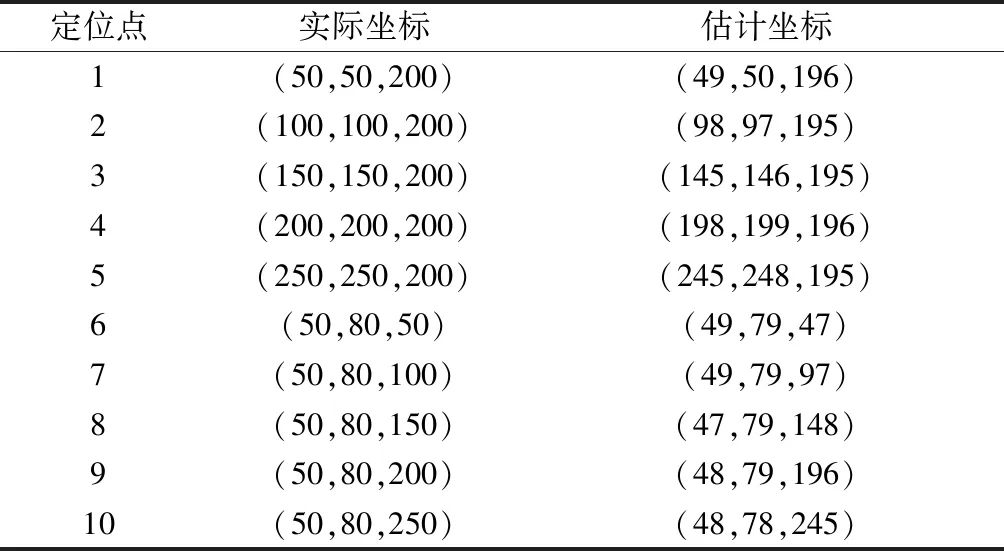
表5 定位結果

由圖7分析可以得到,在UAV高度以及水平距離變化時,定位結果的高度誤差變化相對較大。隨著高度增加,UAV定位誤差也隨著增大,分析這是由于接收基站的實際高度為0到10 m,因此在算法的定位過程中,由于Z軸值太小,導致定位結果在Z軸方向上具有較大的誤差。但是仍然在可接受的誤差范圍內。當UAV水平距離變化時,UAV定位誤差先減小后增大,這是由于UAV過于接近發射基站或離接收基站過近時,UAV與基站之間的距離和基站與基站之間的距離過于接近,導致UAV反射信號與基站之間的直接通信信號到達時間差過小,UAV反射信號淹沒在基站與基站之間直接通信的信號當中,定位精度因此降低。在以大量定位結果與實際UAV坐標進行對比后,以估計的UAV坐標點為中心,計算出半徑為2.6 m的球體內需要定位的實際坐標點,得到2.6 m-CEP(circular error probable)為92.4%,即代表實際UAV定位在以估計目標為圓心,半徑為2.6 m的球內的概率為92.4%。該定位結果明顯優于其他基于移動通信基站對UAV進行定位的算法。仿真結果表明,該定位算法能夠對UAV實現高精度定位。

4 結 論

針對UAV定位中多徑噪聲與高度誤差較大的問題,提出了一種基于隨機森林權重補償的小目標高精度定位算法,利用UAV對移動通信基站信號的反射進行特征提取,并使用標定UAV校正機器誤差,實現對UAV的高精度定位。在距離誤差矩陣中,我們提出了定位距離的權重校正矩陣。根據定位信號的特點,通過交叉驗證得到隨機森林位置模型的決策樹參數。我們通過混淆矩陣和泛化誤差來校正定位數據,并分配相應的權重以最終獲得目標的三維坐標,在此基礎上,使用標定UAV來估計設備誤差,進而得到待估計UAV的坐標信息。結果表明,隨機森林算法比現有的三維空間定位算法定位精度更高,滿足了隨機森林模型與實際的一致性。