基于A3C的多功能雷達認知干擾決策方法

鄒瑋琦, 牛朝陽, 劉 偉, 高歐陽, 張浩波

(信息工程大學數據與目標工程學院, 河南 鄭州 450000)

0 引 言

電子對抗是作戰雙方為保障己方優勢,削弱對方實力而采取的各種電子措施和行動。在現代戰場中,針對雷達的電子對抗扮演著越來越重要的角色,而干擾決策是雷達電子對抗領域的關鍵技術,其任務是對偵察環節所獲取的威脅數據進行分析,快速準確地確定干擾決策,并通過評估環節不斷調整干擾決策,有效完成干擾任務,極大減少對方雷達的威脅。

隨著雷達發展趨于多功能與智能化[1-2],抗干擾能力增強,依賴于“匹配”以及“人為試錯”思想的傳統干擾決策方法[3-4]決策效率低、準確率不高的缺點愈發明顯。為了滿足雷達電子對抗的需求,進行具有認知能力的干擾決策方法研究具有重要意義。為此,文獻[5]將強化學習[6]中的Q-learning方法引入到雷達干擾決策中,使干擾系統能夠通過自主學習確定最佳的干擾策略,但該方案僅適用于雷達工作模式數目已知的情況。因此，文獻[7]針對雷達工作模式數目未知條件完成了智能雷達對抗設計過程,提高了雷達干擾系統的實時性與自適應性。在此基礎上,文獻[8]通過分析多功能雷達工作狀態及對應干擾樣式構建雷達狀態轉移圖,仿真分析了各參數對干擾決策性能的影響,以及在新狀態加入下的決策過程、轉移概率對決策路徑的影響。由于文獻[7]和文獻[8]所提方法隨著多功能雷達可執行任務個數增多而時間效率逐漸下降,文獻[9]將深度Q網絡(deep Q network, DQN)引入到多功能雷達干擾決策中,DQN是Q-learning算法與深度學習的結合,直接使用神經網絡替代傳統表格生成 Q 值,在處理大量狀態空間和動作空間時具有明顯優勢,從而提高了多功能雷達認知干擾決策的時間效率。在干擾決策整體過程中偵察環節、決策環節以及評估環節都需要時間,然而目標方雷達執行任務時間是有限的,雙方的對抗稍縱即逝,因此提高時間效率依舊是認知干擾決策的關鍵。文獻[9]在雷達任務數量為25的條件下循環200次的決策完成時間約為40 s,仍然難以滿足雷達對抗決策的高實時性要求。針對此問題,在充分研究多功能雷達工作模式和任務轉換關系的基礎上,本文提出了一種基于異步優勢行動者-評論家(asynchronous advantage actor-critic, A3C)的認知干擾決策方法,設計了包括干擾機模型、環境模型(目標方多功能雷達)及其交互機制的認知干擾決策整體框架,制定了干擾決策流程。

1 A3C基本原理

A3C算法[10]是Mnih等在異步強化學習(asynchronous reinforcement learning, ARL)理論基礎上提出的一種輕量級深度強化學習算法。該算法引入多線程的概念,使得多個智能體同時進行訓練,極大加快了訓練速度,同時利用異步的方式,確保每個線程的初始狀態和探索方向不同,使得各個線程中樣本相關性降低,從而穩定算法,使得該算法在一些領域有著較好表現[11-12]。

A3C算法在各個線程中延用行動者-評論家[13](actor-critic, AC)算法與深度神經網絡相結合構成的AC網絡(AC network, ACN),利用深度神經網絡的優勢使其有利于處理大規模狀態空間和動作空間的任務,具體結構圖如圖1所示。

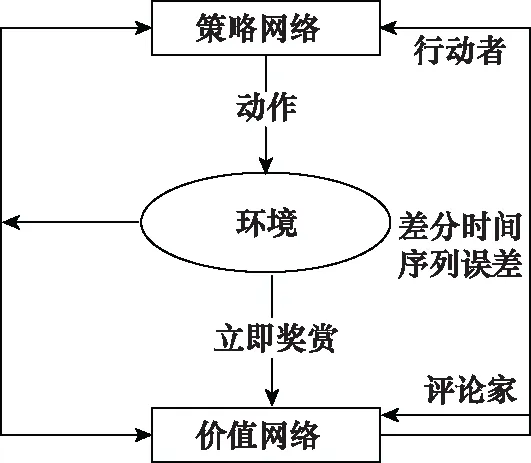
圖1 ACN結構圖Fig.1 ACN structure diagram

ACN利用策略網絡和價值網絡分別表示策略函數和值函數:

(1) 策略網絡π(at|st;θ)是用來更新學習模型的策略,計算在狀態st所采取動作的概率分布,即行動者部分。其中，θ為策略網絡參數。

(2) 價值網絡V(st;θv)用來評價在狀態st執行動作at的優劣,即評論家部分。其中，θv為價值網絡參數。

ACN在進行策略更新的時候,平等對待每一個狀態動作對,然而在訓練過程中,每一個狀態動作對的重要性是不一樣的。針對此問題,A3C算法在ACN結構基礎上引入優勢函數用于評價當前狀態動作對的優勢。優勢函數公式如下:

(1)

式中:rt+i表示即時獎賞;γ∈[0,1]為折扣因子,代表未來獎賞對于累計獎賞的重要程度,當n=1時,其為1步回報優勢函數,當n=k時,其為k步回報優勢函數。該算法策略網絡和價值網絡的損失函數如下所示:

(2)

(3)

式中:R表示智能體在當前狀態下依據策略選擇動作所獲得的回報值;V(st;θv)表示該狀態下的值函數。

為防止過早收斂到局部最優,A3C算法將策略交叉熵加入到策略網絡損失函數aloss中,保證策略進行廣泛搜索。

(4)

式中:H(π(st,θ)),為策略交叉熵;c為熵系數,用于控制熵的正則化強度。

2 基于A3C的認知干擾決策方法

由于A3C算法有利于處理大規模狀態空間的任務,并且具有多線程處理能力,計算速度快。本文將A3C強化學習算法應用于認知干擾決策領域,設計了認知干擾決策整體框架,具體如圖2所示。其主要包括全局網絡以及多個干擾線程。全局網絡相當于是一個中央大腦,將各個干擾線程網絡參數進行匯總分發。干擾線程包括干擾機模型、環境模型(目標方多功能雷達)以及交互機制,干擾機模型通過干擾樣式選取、雷達任務狀態描述以及干擾樣式有效性評估3個途徑與環境進行交互訓練。

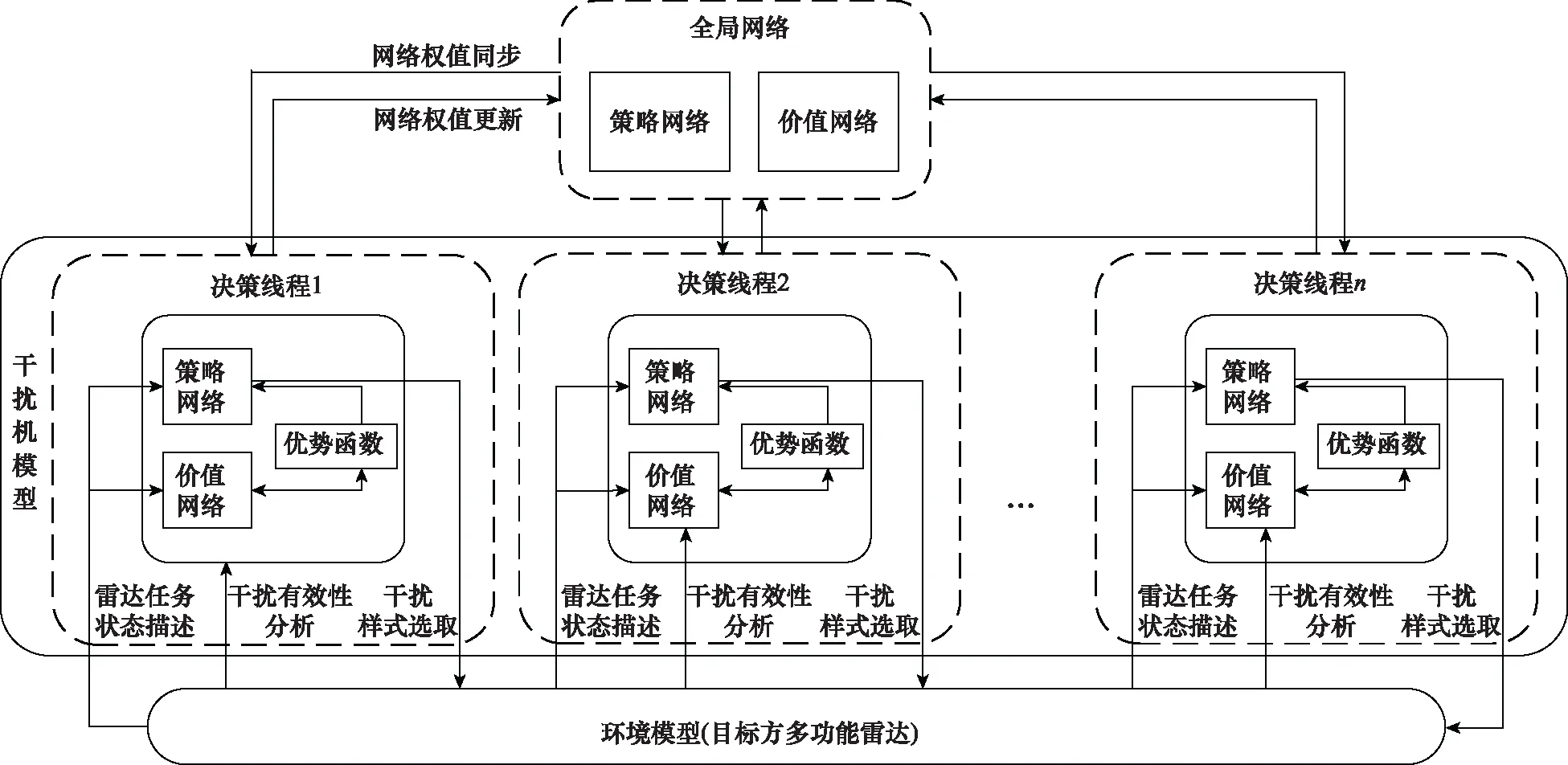
圖2 認知干擾決策整體框架Fig.2 Cognitive jamming decision-making overall framework

2.1 全局網絡

全局網絡由兩部分組成,一是策略網絡,其功能是在當前雷達任務狀態st下,計算所采取的干擾樣式at;二是價值網絡,其功能是對當前雷達任務狀態st下所采取的干擾樣式at進行評估。全局網絡與各線程網絡具有相同結構,但全局網絡自身不進行訓練,依托于各個線程中的干擾機模型獨立與環境交互進行訓練,其僅存儲各個線程中干擾機模型策略網絡和價值網絡的網絡參數,同時將自身的網絡參數同步至各個線程中的干擾機模型。

2.2 干擾線程

如圖2所示,干擾線程主要包括干擾機模型、環境模型(目標方多功能雷達)及其交互機制。

2.2.1 干擾機模型

干擾機模型包括價值網絡和策略網絡。價值網絡的輸入為雷達任務狀態,輸出為采取干擾樣式的值函數,并依據值函數與對應回報值得到優勢函數。策略網絡的輸入為多功能雷達某時刻所執行的雷達任務狀態以及優勢函數,輸出為干擾機所采取的干擾樣式。策略網絡基于概率采取相應干擾樣式,然后價值網絡判斷策略網絡采取干擾樣式的好壞,策略網絡再依據評價值調整網絡參數。

2.2.2 環境模型(目標方多功能雷達)

環境模型描述目標方多功能雷達被策略網絡輸出的干擾樣式干擾后，雷達任務的變化情況。當干擾機模型實施選定的干擾樣式后,雷達任務狀態便發生了相應的變化,為更有效表明干擾前后雷達任務狀態的變化情況,本文采用文獻[9]中雷達任務關系轉換表的方式建立環境模型。

2.2.3 干擾機模型與環境交互機制

各個線程內干擾機模型與環境之間的交互機制主要包括干擾樣式選取、雷達任務狀態描述和干擾樣式有效性評估3個途徑。

(1) 干擾樣式選取

干擾機所采取的干擾樣式來源于干擾信息庫,其基本結構如圖3所示。干擾信息庫主要包括雷達威脅數據以及干擾機干擾數據,其中雷達威脅數據部分主要依據多功能雷達信號層級模型[14-15],包括雷達功能層、雷達任務層以及相應波形單元特征向量,負責提供目標多功能雷達的威脅信息。由于當雷達處于不同功能不同任務時,其波形單元不相同,干擾機所采取的干擾樣式不盡相同,因此干擾數據部分為雷達的具體功能和任務下對應的有效干擾樣式集合。

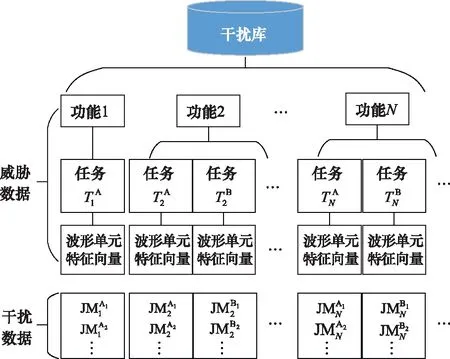
圖3 干擾信息庫基本結構Fig.3 Basic structure of jamming information library

(2) 雷達任務狀態描述

依據多功能雷達信號層級模型構建雷達任務關系表,如表1所示。

表1 雷達任務關系表

當偵測到多功能雷達某時刻執行雷達任務狀態,獲取該狀態下功能層對應的數值(即x值)以及任務層對應的數值(即y值),得到其當前狀態坐標值(x,y),并利用當前狀態坐標值與目標狀態(雷達威脅等級最低)坐標值的差值描述雷達任務狀態st。

(3) 干擾樣式有效性評估

文獻[9]利用雷達任務的轉換關系來對干擾樣式進行有效性分析。對于多功能雷達而言,其雷達任務有著一定的優先級排序,雷達任務的優先級越高,則意味著其對乙方的威脅等級越高。如果干擾機實施選定的干擾樣式后雷達任務的優先級(即威脅等級)降低,則選定的干擾樣式有效;如果雷達任務的威脅等級未發生變化或者升高,則選定的干擾樣式無效。

文獻[9]獎勵函數僅將雷達威脅等級變化設置為上升和下降兩種狀態,未考慮威脅等級數變化不同的情況,因此本文對獎勵函數進行修正,將變化的威脅等級數與對應的獎賞值相對應,使得獎勵函數的設置更加準確,能夠更有效體現采取干擾樣式的有效程度。具體設置如下:

(5)

式中:Tn→Tend表示雷達威脅等級轉變至最低的狀態;Tn→Tn表示雷達威脅等級維持不變;Tn→Tn-i表示雷達威脅等級升高i個等級;Tn→Tn+i則表示雷達威脅等級降低i個等級。

(4) 交互機制

綜合上述3個途徑,任意干擾線程內干擾機模型與環境交互機制具體如下所示。

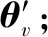
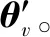
算法 1 基于A3C的認知干擾決策輸入 干擾樣式合集J,全局共享的迭代次數T,全局最大迭代次數Tmax, 干擾線程內迭代次數t,干擾線程內迭代最大次數tmax,學習率η,衰減因子γ,熵系數c步驟 1 t←1,T←0;步驟 2 重置策略網絡和價值網絡的梯度更新量:dθ←0、dθv←0,并將全局網絡同步參數到本線程干擾機模型的神經網絡:θ′=θ,θ′v=θv;步驟 3 初始化雷達任務狀態st,即雷達威脅等級最高狀態,并記錄該狀態下線程內迭代次數tstart=t;步驟 4 基于策略π(at|st;θ′)得到干擾樣式概率分布,選取干擾樣式at;步驟 5 針對目標方雷達采取干擾樣式at,并獲取新雷達任務狀態st+1;步驟 6 獎賞rt依據變化前后雷達任務狀態st,st+1,對照式(5)獎勵函數得到即時獎勵rt;步驟 7 t←t+1,T←T+1;步驟 8 如果st+1對應雷達威脅等級最低狀態,或者t-tstart,則進入步驟9,否則回到步驟5;步驟 9 對照步驟8中進入步驟9的兩個條件計算最后一次迭代狀態st的對應的R:R=0, 終止狀態 stV(st,θv), 非終止狀態 st {步驟 10 for i∈{t-1,t-2,…,tstart}: (1) 計算每個時刻的R:R←ri+γR (2) 累計策略網絡的本地梯度更新:dθ←dθ+Δθ′ln π (ai|si;θ′)(R-V(si;θ′v))+Δθ′H(π (si,θ′)) (3) 累計價值網絡的本地梯度更新: dθv←dθv+?(R-V(si;θ′v))2?θ′v步驟 11 更新全局神經網絡的模型參數:θ=θ-ηdθ, θv=θv-ηdθv步驟 12 如果T>Tmax,則算法結束,否則進入步驟2。

上述基于A3C的認知干擾決策方法能夠形成一個實時的閉環結構,干擾機模型能夠與環境模型進行自主交互并形成有效干擾決策,表明該方法具有可靠性。同時，該方法為提升時間效率采用了異步的思想,每個干擾線程中干擾機模型的初始狀態和探索方向不同,通過共同探索并行計算策略梯度,對參數進行更新,能夠最大化探索多樣性,確保該方法的穩定性。

3 仿真實驗

本文仿真實驗環境在個人計算機上搭建,其處理器為Inter(R)Core(TM) i7-10875H CPU@2.30 GHz,擁有8個內核以及16個邏輯處理器;GPU為NVIDIA GeForce RTX 2080,算法采用Python語言和PyTorch深度學習框架進行編寫。

本文基于A3C的認知干擾決策方法采用自適應矩估計(adaptive moment estimation, Adam)梯度下降法來進行網絡參數更新,具體參數設置如下:學習率η=0.01、一階矩估計衰減率β1=0.9,二階矩估計衰減率β2=0.99、超參數ε=10-8,折扣因子γ=0.9。該方法的異步更新方式如下:實驗利用16個線程加速訓練,每10步或者當前回合結束更新一次網絡參數。基于DQN的認知干擾決策方法設置學習率為η=0.01,折扣因子γ=0.9,記憶庫總量為2 000,每隔200步估計值網絡的參數并傳遞至真實值網絡。Double DQN和Prioritized Replay DQN是DQN的兩種改進算法,依據文獻[9]的思路將其應用至多功能雷達對抗的認知干擾決策中,作為本文新方法的對比對象,參數設置與基于DQN的認知干擾決策方法一致。

為討論本文所提方法在雷達任務復雜情況下的決策性能,將文獻[9]的雷達任務轉換關系表的雷達威脅等級由11個擴充至15個,如表2所示。依據該表進行10次獨立實驗,每次實驗模擬5 000個回合,并對比分析本文所提方法和基于DQN的認知干擾決策系列方法(DQN、Double DQN和Prioritized Replay DQN)的模型訓練時間和移動平均獎賞相對值。

表2 雷達任務轉換關系表

3.1 模型訓練時間

表3數據為不同方法的平均每回合所用時間,圖4為不同方法的5 000回合模型訓練時間對比圖,其中圖4(a)為平均每回合時間,圖4(b)為累計時間。

表3 平均每回合所用時間比較

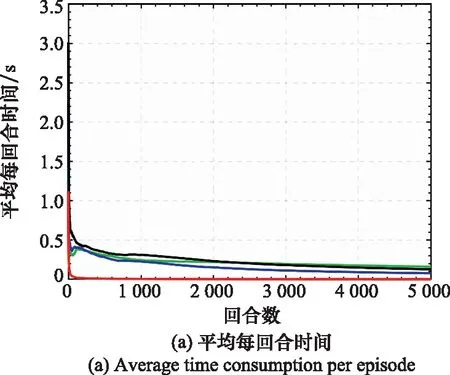
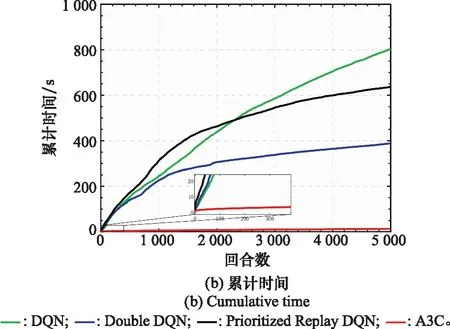
圖4 模型訓練時間對比圖Fig.4 Comparison diagram of model training time

從表3中可以看出,相較于基于DQN的認知干擾決策方法,其他3種認知干擾決策方法的平均每回合所用時間均有一定的降低,其中本文所提方法優勢最明顯,將平均每回合所用時間降低約40%。

從圖4(a)可以看出,基于A3C的認知干擾決策方法從一開始平均每回合時間便大幅度低于基于DQN的認知干擾決策系列方法,并在整個階段保持明顯優勢。分析原因,基于A3C的認知干擾決策方法具有多線程處理能力,相當于多個干擾機模型并行工作,相較于單線程方法而言優勢更加明顯,能極大提高時間效率。并由圖4(b)局部放大的小圖可以看出,該時間曲線并不是線性的,與基于DQN的認知干擾決策系列方法相似,都是類似對數的變化趨勢,干擾機模型在工作過程中隨著回合數的增加,所獲得經驗不斷積累,每回合所采取的有效干擾樣式逐漸減少,相應每回合所用時間不斷降低。

綜上所述,本文所提方法在雷達任務復雜情況下極大提高了時間效率,更能夠滿足雷達對抗高實時性要求。

3.2 移動平均獎賞相對值

定義移動平均獎賞如下:

Ri=βRi-1+(1-β)ri

(6)

式中:Ri為當前回合移動平均獎賞;Ri-1為上一回合移動平均獎賞;ri為當前回合獎賞值;β為權重因子,此處取0.99。為使移動平均獎賞能夠更直觀呈現,本文采取移動平均獎賞相對值,其定義如下:

Rrv-i=Ri/Rmax

(7)

其中，Rrv-i為當前回合移動平均獎賞相對值；Rmax表示單次回合獎賞的理論最大值。移動平均獎賞相對值越高,表示干擾機模型每回合在進行決策的過程中有效干擾樣式更多,表示其決策準確度更高。

由于在訓練的過程中,網絡參數不斷更新,非常小的變化都可能導致下一階段的決策產生大的變動,導致移動平均獎賞相對值在不同回合階段會出現不同程度的波動,因此本文采取進行10次單獨實驗最后取平均的方式來反映總體趨勢。

圖5為不同方法的移動平均獎賞相對值曲線圖。由圖5可得,在1 500回合之內,本文所提方法相較于其他方法而言有著大幅度的優勢,在1 500回合之后,兩種改進的DQN認知干擾決策方法逐漸靠近本文所提方法,但基于DQN的認知干擾決策方法效果依舊不理想。分析原因,由于DQN算法存在訓練效率低、過估計以及記憶能力有限等缺陷,導致相應方法在雷達任務復雜情況下效果不理想。Double DQN和Prioritized Replay DQN在DQN算法的基礎上進行改進,效果有著一定的提升,本文所提方法則在引入優勢函數以及策略交叉熵的同時,利用異步的方式確保每個線程的初始狀態和探索方向不同,最大化干擾機模型探索環境的多樣性,并且能夠降低數據的相關性,提升該方法的穩定性,使得決策準確度有明顯提高。

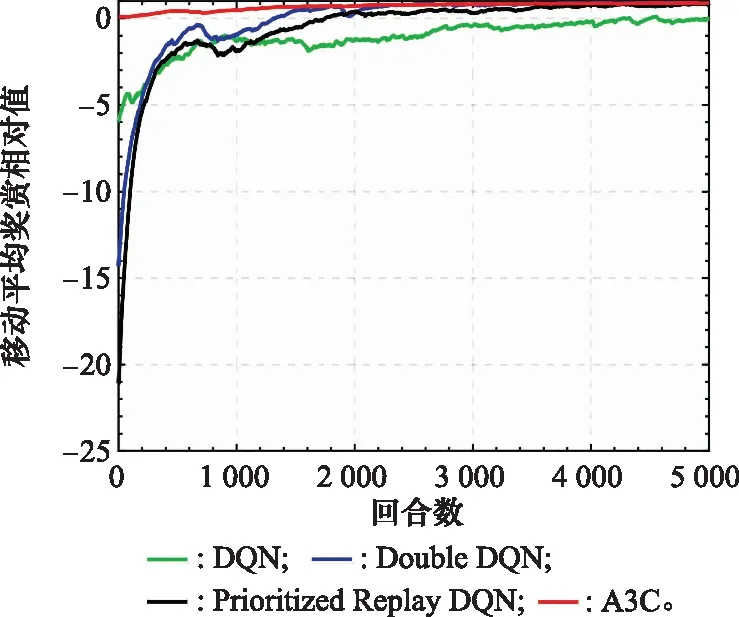
圖5 移動平均獎賞相對值對比圖Fig.5 Comparison diagram of moving average reward relative value

綜上所述,在雷達任務復雜情況下,本文所提方法有著更好的決策準確度。

從綜合模型訓練時間以及移動平均獎賞相對值的對比可以看出,在雷達任務轉換關系表擴充條件下,本文方法與基于DQN的認知干擾決策系列方法相比,極大地提高了時間效率,平均決策時間降低30倍以上,同時在移動平均獎賞相對值中所展現的決策準確度上也有明顯優勢。由此可以看出,在雷達發展趨于多功能化以及雷達對抗趨于智能化的背景下,本文所提方法更能夠適應高實時性的復雜雷達對抗環境。

4 結束語

在雷達對抗領域,雷達越來越趨于多功能化和智能化,對認知干擾決策的時間效率和決策準確度要求更高。對此,本文提出一種基于A3C的認知干擾決策方法。研究表明,該方法能夠在雷達任務數量更為復雜的情況下,極大地提高時間效率,并在決策準確度上有著明顯優勢。

在認知干擾決策領域,進一步提高實時性、縮短對抗時間是關鍵所在,同時針對雷達態勢識別和干擾效能評估也是下一步的研究重點。