基于SINS/GBAS組合導航的高精度進近著陸導航技術

高利春, 高銘陽, 陳曉芳, 饒建兵, 費澤松, 倪少杰

(1. 中國航天科工集團空間工程總體部, 北京 100854; 2.武漢理工大學管理學院, 湖北 武漢 430070;3. 北京理工大學信息與電子學院, 北京 100081; 4. 國防科技大學電子科學學院, 湖南 長沙 410003)

0 引 言

可重復使用運載器通過重復使用有效地降低了單次發射費用,從而降低了發射成本,因此成為了近代航空航天發展的重點研究對象。進近著陸飛行段作為運載飛行器著陸的最后階段,對于飛行器的導航和控制系統提出了更高的要求。為了滿足可重復使用運載器的著陸要求,發展一種高精度、高可靠性、可應對各種復雜外界環境影響的導航系統至關重要[1-2]。

陸基增強系統(ground based augmentation system,GBAS)[3]是一套廣泛應用于民用航空客機進場的導航系統,例如可對航空客機以及小型無人機控制進場進行準確導航[4]。相比常規使用的儀器降落系統(instrument landing system, ILS),GBAS有更高的精確度、完整性、可用性以及連續性。除最早發展的美國區域增強系統(local area augmentation system, LAAS)外,中國[5]、日本[6]、韓國[7]、德國[8]等國家均開發建立了獨立的GBAS。相比差分全球定位系統(differential global position systems, DGPS), GBAS通過地面基站的差分信息修正傳統GPS定位中的偽距偏差,從而有效地提高了可重復使用運載器在進近著陸段的導航精度。張羽成等[9]利用GBAS為傳統的位置觀測方法提供了差分修正,解決了大型無人機傳統單點定位精度低、可靠性差的問題。然而極端氣象環境,例如太陽耀斑、熱帶風暴對于對流層、電離層等的外界影響[10],使得單一導航方法難以滿足航天航空運載器精確導航的需求[11-12]。Wang等[13]通過對在廣州的65個基準基站的GBAS的數據分析,發現在太陽耀斑影響下，垂直方向的導航標準偏差從正常的0.8 m升高至約5 m。

為了滿足當前航天航空對于導航系統的高精度、高可靠性、自主隱蔽、全球全天候的導航保障能力的要求[14],組合導航是未來航天航空導航技術發展的必然趨勢[15]。GBAS作為全球衛星導航系統下的子系統[16-17],可有效與其他導航方式組合,從而滿足高精度和高可靠性要求。例如,通過GPS結合GBAS導航系統[18-19],實現了全天候、在全球范圍內對導航載體提供即時三維位置、速度與姿態等詳細的導航信息。此外，王勛等[20]在2016年提出了捷聯慣導系統(strap-down inertial navigation system, SINS)結合GBAS,實現了SINS/陸基單站組合導航模塊,通過對松組合導航系統和緊組合導航系統進行建模與仿真性能驗證，發現對于緊組合系統，“東-北-天”位置誤差均值約為0.27 m,誤差標準差約為2 m,而松組合系統的導航誤差波動幅度較大,標準差為4.0 m。其誤差尚不滿足運載器對高精確導航的要求,并且外界環境(例如對流層以及電離層)的影響未考慮在內。相比現有的衛星導航系統[21],GBAS具有較高精度的接收信號以及更強的抗噪聲干擾能力,因此基于GBAS的組合導航方式依然是衛星導航系統重要的輔助以及備份方法[22-23]。然而,現有的GBAS組合導航方式尚處于發展初期,極端環境、導航精度以及誤差時間漂移對于基于GBAS組合導航的影響尚不明確。

因此,本文提出了基于SINS/GBAS組合導航的高精度進近著陸導航方法,利用SINS的連續性與高可靠性,提高了在GBAS故障時系統的魯棒性,解決進近著陸系統的連續可用性問題。通過引入電離層誤差以及對流層誤差,計算了在極端條件下不同衛星的仰角隨時間變化的曲線,從而實現了對于運載器定位誤差在厘米級尺度的精確定位。此外,我們運用擴展卡爾曼濾波技術有效地抑制了SINS誤差隨時間漂移的問題。我們提出的SINS/GBAS組合導航為現今可重復使用運載器的高精度進近著陸導航設計提供了新思路。

1 慣性導航系統建模

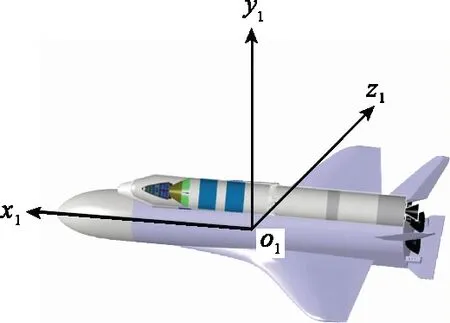
圖1 運載器本體系定義Fig.1 Body coordinate system

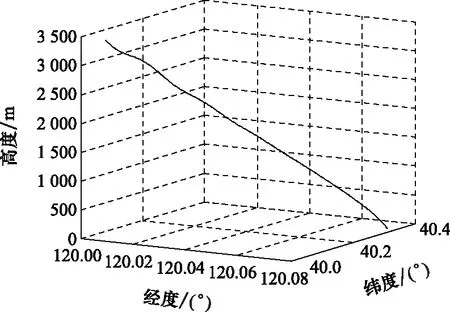
圖2 三維標稱軌跡曲線Fig.2 Three dimensional nominal trajectory curve

我們采取“光纖陀螺儀+石英加速度計”作為慣性導航模型的敏感器，并在表1中列出慣性導航的相關技術指標。圖3～圖8為通過數值仿真,慣性導航系統在三維坐標系中視加速度以及角速度的變化曲線。

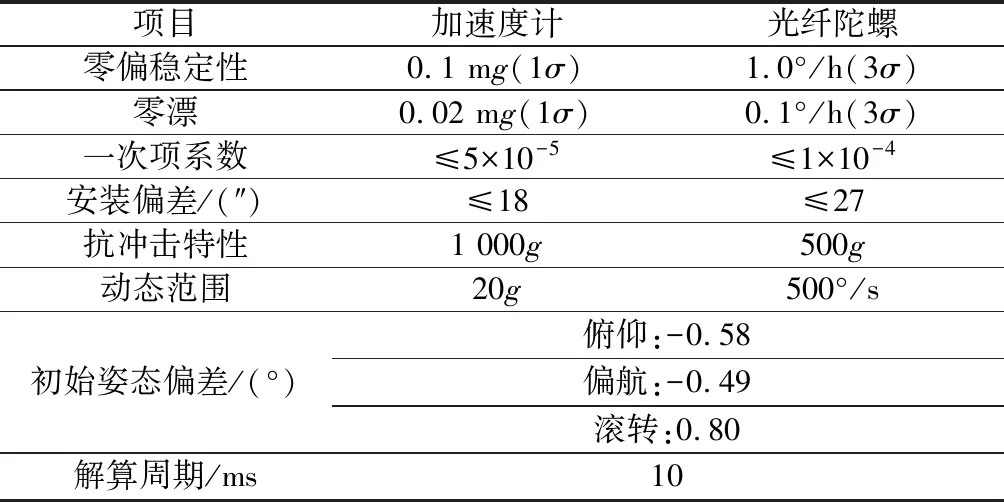
表1 加速度計與光纖陀螺指標參數

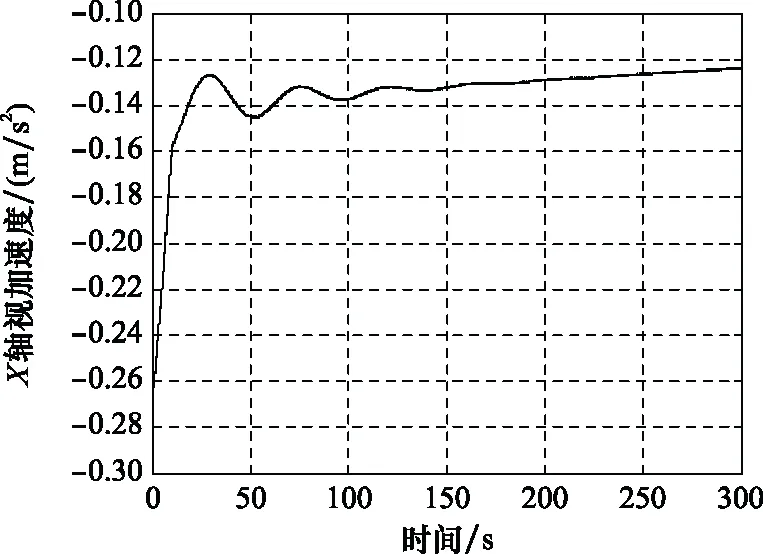
圖3 X軸視加速度變化曲線Fig.3 X axis apparent acceleration curve

圖4 Y軸視加速度變化曲線Fig.4 Y axis apparent acceleration curve

圖5 Z軸視加速度變化曲線Fig.5 Z axis apparent acceleration curve

圖6 X軸角速度變化曲線Fig.6 X axis angular velocity curve

圖7 Y軸角速度變化曲線Fig.7 Y axis angular velocity curve

圖8 Z軸角速度變化曲線Fig.8 Z axis angular velocity curve

2 衛星導航GBAS

本節首先討論GBAS的解算方法以及仿真實驗,并對現有常見的3種導航方法,包括之前提到的傳統衛星導航GPS、衛星增強系統GBAS,以及DGPS進行仿真實驗,并比較了3種導航定位方法的定位誤差曲線。最后,討論外界因素對于GBAS的誤差影響以及修正算法。

2.1 GBAS誤差分析及修正算法

由于可重復使用運載器的機載導航系統可自主完成運載器多用戶效應所產生的接收器誤差的修正,我們主要討論地面接收機誤差、電離層延遲以及對流層延遲對于GBAS地面設施的相關修正參數的影響。

2.1.1 地面接收機誤差

假設地面基準接收機的數量為4,GBAS地面接收機的精度等級為B級,則接收機誤差的計算公式[24]為

(1)

式中:θ為地面基準接收機與衛星間的仰角。

根據式(1)計算地面接收器誤差隨衛星仰角在1°～90°的變化趨勢。如圖9所示,地面接收機觀測誤差隨著衛星仰角的增加而減少,其誤差范圍為0.1～0.6 m。當仰角為90°時誤差最小,為0.1 m。

圖9 地面接收機誤差隨衛星仰角變化曲線Fig.9 Ground receiver error change curves with the satellite elevation angle

2.1.2 電離層誤差

電離層誤差修正的計算公式[24]為

(2)

式中:h1為電離層高度;Re為地球半徑;xair為可重復使用運載器與地面基準接收機的斜距;vair為可重復使用運載器在水平方向的速度。

首先模擬計算運載器與地面接收機的斜距xair(見圖10)以及運載器在水平方向上的速度vair(見圖11)。在分別建立xair和vair與時間的關系時利用式(2)進行仿真,從而計算出如圖12所示的不同衛星仰角下電離層誤差隨時間的變化曲線。

如圖10和圖11所示,在運載器的進近著陸段,運載器的高度隨著時間的增加而減小,因此運載器與接收器的斜率以及水平方向上的速度隨著高度的降低而減小。此外,我們建立了在不同衛星仰角下電離層誤差與時間之間的關系。如圖12 所示,當衛星仰角一定時,電離層誤差隨著時間的增加而減小。對于相同的運載器高度,即相同的時間,電離層的誤差隨著衛星仰角的增加而減小。

圖10 運載器與基準接收機的斜距變化曲線Fig.10 Slope distance change curves between vehicle and ground receiver

圖11 運載器在水平方向上的速度變化曲線Fig.11 Horizontal velocity curve of vehicle

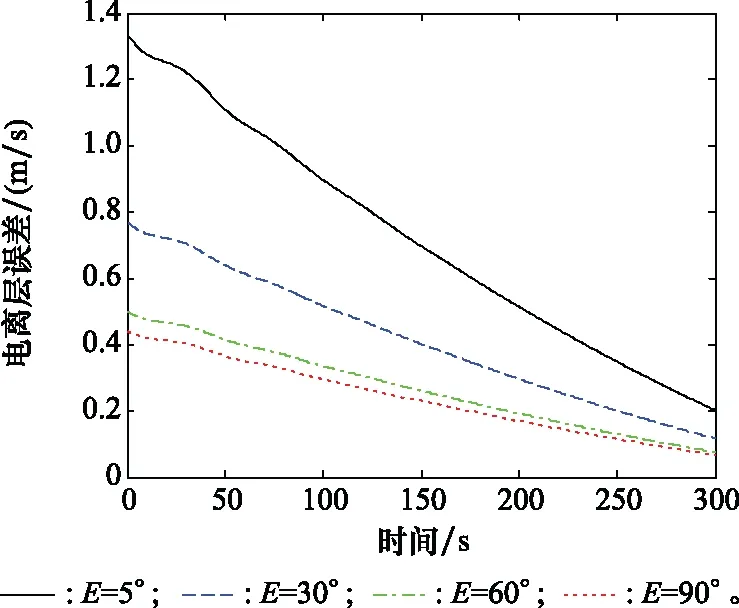
圖12 不同衛星仰角下電離層誤差隨時間變化曲線Fig.12 Ionospheric error curve with the different satellite elevation angles

2.1.3 對流層誤差

計算對流層延時(TC)以及修正誤差(σtropo)與運載器高度之間的關系,其計算方法[25]為

(3)

(4)

式中:NR為對流層折射指數;h0為均值大氣高度;σN為折射不確定度;h為運載器相對于地面基準接收站的高度。

2.1.4 仿真算例

根據酒泉某氣象站的2019年全年的日平均溫度、濕度以及氣壓,計算了年平均的大氣層高度為16 698.1 m以及年折射不確定度為11.3。此外,我們選取了發射日當天的對流層的折射高度,并代入式(3)和式(4)計算對流層延時誤差以及修正誤差,從而仿真模擬兩種誤差與衛星仰角的關系。

當運載器相對于地面基準站的高度為定值時,TC和σtropo隨著衛星仰角的增加而減小,對于相同的衛星仰角而言,TC和σtropo隨著相對高度的降低而逐漸降低。

圖13與圖14為對流層延時誤差以及修正誤差隨著衛星仰角的變化曲線。

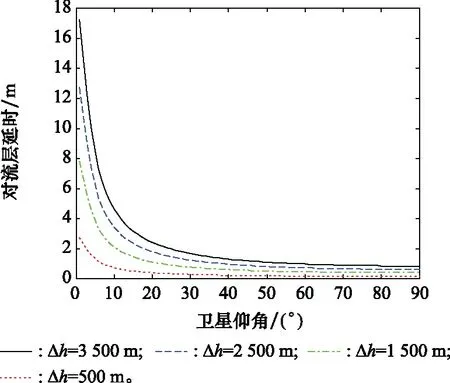
圖13 對流層延時誤差隨衛星仰角變化曲線Fig.13 Tropospheric delay correction change curves with the satellite elevation angles

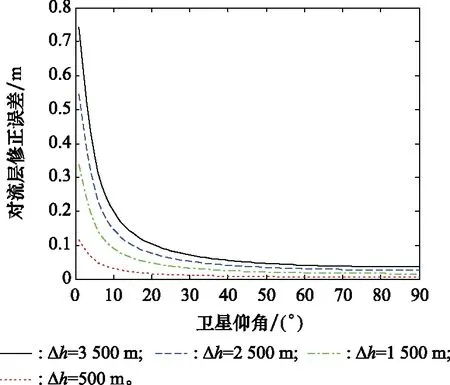
圖14 修正誤差隨衛星仰角變化曲線Fig.14 Error correction change curves with the satellite elevation angles

在相同的衛星仰角下,隨著可重復使用運載器與地面基準站相對高度的減小,兩種誤差,即對流層延時誤差與修正誤差均逐漸減小,當相對距離為500 m時,對流層延時誤差小于2 m,對流層修正誤差小于0.2 m。當相對距離一定時,對流層延時誤差與修正誤差隨著衛星仰角的減小呈指數型降低。在相同的衛星仰角以及相對高度下,對流層延時誤差高于對流層修正誤差一個數量級。因此，在可重復使用運載器的進近著陸段,高衛星仰角的對流層延時誤差為影響運載器精確定位的主要因素。

2.2 GBAS仿真實驗

為了驗證GBAS增強慣性導航的性能，與其他的組合導航方式進行比較,在本節我們設置了3種不同的仿真條件(即GPS、DGPS以及GBAS與SINS組合導航)進行仿真模擬。本節所采用的軌跡數據與圖2的標稱軌跡相同。相比GPS[26-27]與DGPS[28]并未對運載器測量所得的偽距數據進行差分處理或僅對偽距修正量和偽距修正變化量進行修正,GBAS導航方法還引入了如前文所討論的對于對流層以及電離層延時的修正,從而有效地提高了導航的精度。

圖15～圖17為3種不同組合導航方法下X、Y、Z方向的定位誤差曲線。傳統衛星GPS導航的定位精度較差,在X、Y、Z3個方向上均存在較大的波動,其波動誤差范圍為±6 m,難以滿足近代運載器在進近著陸段的導航要求。采用DGPS方法,即引入偽距修正量以及偽距修正變化率之后,在X、Y、Z3個方向的定位誤差均有明顯的降低。但當運載器距離地面接收器距離較遠,即處于進近著陸初段時,由于未考慮對流層厚度對于導航的影響,在著陸的初始段，導航定位誤差較大,在Y和Z方向導航誤差約為±1 m。隨著高度的逐漸降低,定位誤差也逐步減小。這也與我們之前所討論的由對流層延時誤差所造成的定位誤差相吻合。而本文中采取的GBAS方法,引入了外界條件影響,特別是引入了由對流層厚度所產生的對流層延時誤差補償之后,在進近著陸全部階段中,定位誤差明顯減小,達到了厘米級別，有效地滿足可重復使用運載器的進近著陸段的導航要求。

4.1 主管部門的關注是武術對外教材沖破困境的主要動力 國際武術聯合會、中國武術協會等相關部門應該重視目前武術對外教材面臨的主要問題，在政策上給予支持。首先，主管部門應該建立長效機制，將教學出版物“走出去”作為中國武術“走出去”戰略規劃的主要內容。其次，制定詳細的發展規劃，在一定時間內完成相關出版物的編寫與出版。然后，政府部門應投入科研基金，加大該項目科研實施力度，鼓勵相關專業領域學者積極從事相關科研工作，在教材編寫、影像錄制工作中重視成果的產出與轉化，積極推動出版物“走出去”。最后是提升相關出版單位的把控力與版權運作能力，為出版物走向海外鋪平道路，讓武術對外教材“走出去”更加順利。

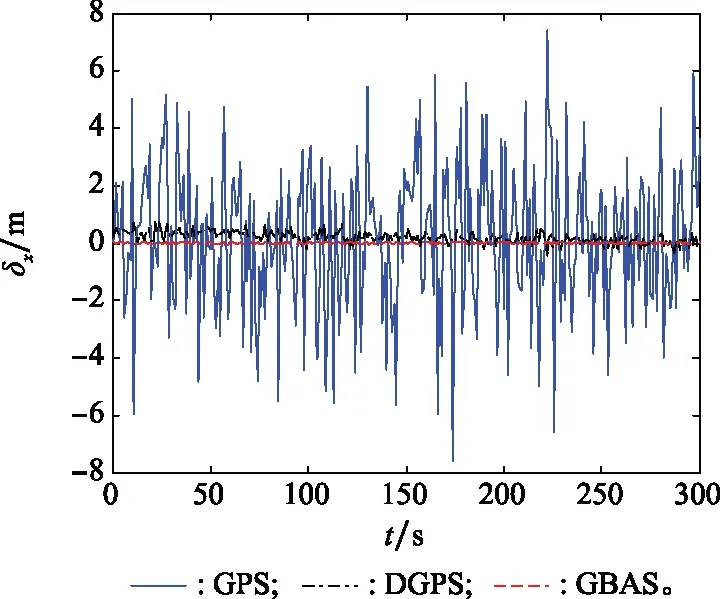
圖15 GPS、DGPS和GBAS在X方向的誤差曲線Fig.15 X axis position error curve among GPS、DGPS and GBAS

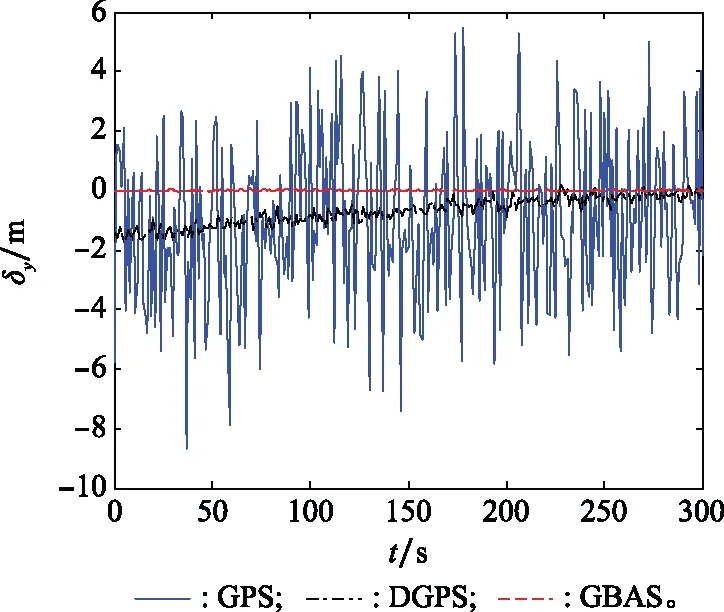
圖16 GPS、DGPS和GBAS在Y方向的誤差曲線Fig.16 Y axis position error curve among GPS、DGPS and GBAS

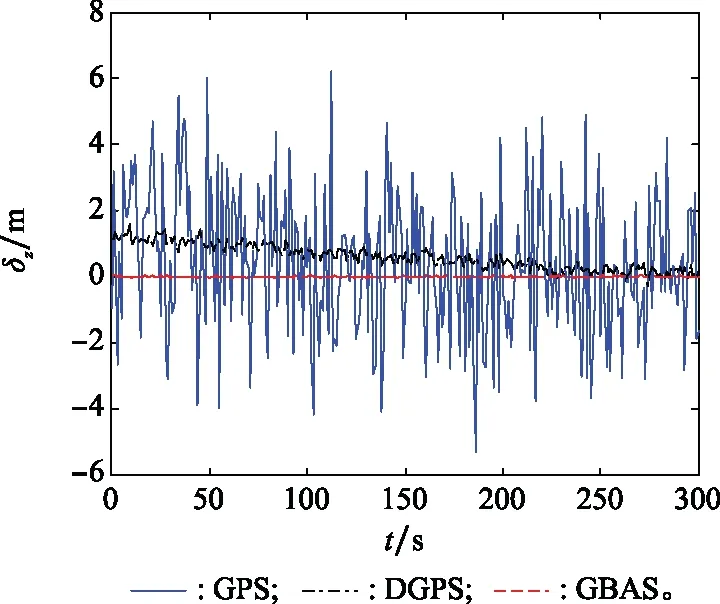
圖17 GPS、DGPS和GBAS在Z方向的誤差曲線Fig.17 Z axis position error curve among GPS、DGPS and GBAS

3 SINS/GBAS組合導航系統建模

運載器在進近著陸過程中,不僅需要高精度的飛行器位置信息,對于飛行器的姿態與速度信息也提出了較高的精度要求。這種高精度的飛行器姿態參數在傳統的組合導航系統中一般是采用卡爾曼濾波算法實現的。

然而，這種組合導航卡爾曼濾波器主要基于線性化慣性導航系統模型,在長時間著陸段的導航過程中，系統中存在著非線性誤差的積累,從而導致間接觀測通道的濾波方法精度下降。因此,我們采用了擴展開爾曼濾波算法作為SINS/GBAS組合導航系統的核心算法,有效地提高了組合導航的精度,并可提供高精度飛行器姿態與速度的信息。我們對導航器件的誤差特性以及來源進行了詳細分析并通過“輸出+反饋”的方法對組合導航系統中的非線性誤差進行抑制,從而有效地提高了物理導航器件以及組合導航濾波器的匹配程度。

3.1 SINS/GBAS組合導航擴展卡爾曼濾波器設計

3.1.1 SINS/GBAS組合導航狀態模型

首先，我們引入了擴展卡爾曼濾波器，對慣性器件以及衛星導航設備的白噪聲進行矯正,運載器在進近著陸過程中,姿態運動較為平穩,綜合考慮計算復雜度與模型精度,選取15維狀態向量x為

x=

[δL,δλ,δh,δVE,δVN,δVU,φN,φU,φE,υx,υy,υz,εx,εy,εz]T

(5)

狀態方程為

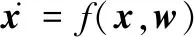
(6)

式中:f(·)表示非線性狀態傳遞過程;w為系統過程噪聲。

一般而言,SINS/GBAS組合導航利用地面接收器測量飛行器的高精度位置信息,并以GBAS所輸出的位置信息作為基準,從而測量SINS的位置偏差,這里的位置偏差又稱為組合導航的觀測值:

Zk=[δL,δλ,δh]T

(7)

其中,觀測方程為

Zk=HkXk

(8)

式中:Hk為3×15維的觀測矩陣,其非零元素為

(9)

3.2 GBAS輔助慣性導航修正策略

在本文中，我們采用了“輸出+反饋”的復合校正結構,有效地提高了系統的魯棒性。其基本示意圖如圖18所示。根據慣性器件的指標參數計算了組合導航系統姿態估計所需的時間,并在反饋周期到來前,通過組合導航濾波器的估計值,對組合導航輸出進行修正并對慣性導航的積分初始值進行修正，從而有效地抑制了慣性導航中的慣導偏移。此外,該組合導航模型可以保證在GBAS失效時進入純慣性導航模式,進一步提高了系統的魯棒性。

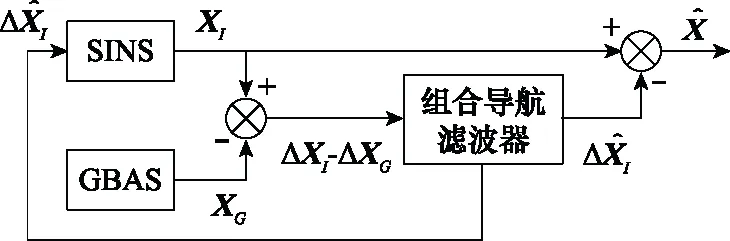
圖18 “輸出+反饋”復合校正組合導航結構圖Fig.18 “Output+feedback”composite correction integrated navigation organization chart

3.3 GBAS組合導航系統仿真分析

為了驗證SINS/GBAS組合導航算法的可行性以及精度,建立了SINS/GBAS組合導航的仿真模塊,并采用表1中SINS的初始仿真條件,對SINS/GBAS組合導航方案的可行性進行了論證。此外,為了對比不同導航方式下的導航精度的差異,我們同時對比了相同標稱軌跡下的兩種組合導航方式,即SINS/GBAS與SINS/GPS組合導航的精度,其仿真初始條件如表2和表3所示。

表2 SINS/GBAS組合導航仿真初始條件

表3 SINS/GPS組合導航仿真初始條件

3.3.1 進近著陸段SINS/GPS組合導航仿真結果

在長時間導航過程中，慣性導航的定位誤差隨著時間的延長也會逐漸積累,通過結合GPS可減小長期導航誤差,從而彌補慣性導航長期導航的劣勢,因此SINS/GPS組合導航在飛行器以及跑車中被廣泛應用[26-27]。與SINS/GBAS組合導航相類似,SINS/GPS組合導航通過引入卡爾曼濾波算法,可以有效地提高飛行器的導航位置與速度精度,位置精度達到5 m,速度精度達到0.1 m/s[29],SINS/GPS組合導航位置誤差是純慣導誤差的1/20,速度誤差是純慣導誤差的1/6[30]。因此,在本文中我們選用SINS/GPS組合導航作為對照組,對比SINS/GPS與SINS/GBAS組合導航的導航精度。數值仿真得到SINS/GPS組合導航的導航參數誤差曲線如圖19～圖26所示。

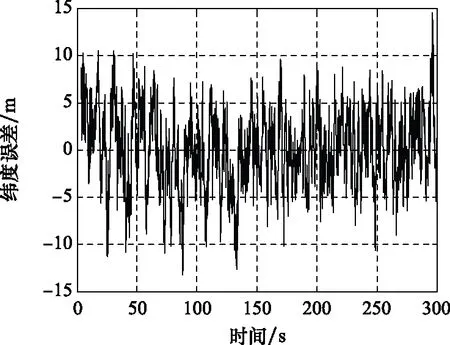
圖19 SINS/GPS組合導航緯度誤差曲線Fig.19 SINS/GPS integrated navigation latitude error curve

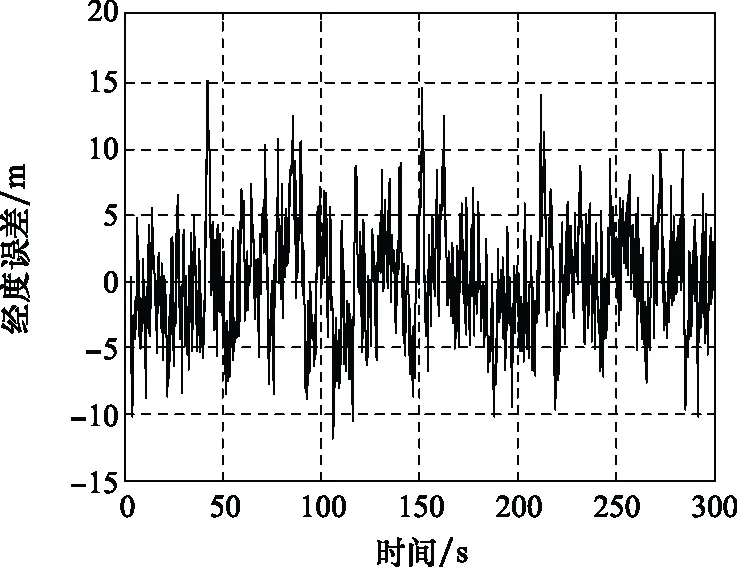
圖20 SINS/GPS組合導航經度誤差曲線Fig.20 SINS/GPS integrated navigation longitude error curve

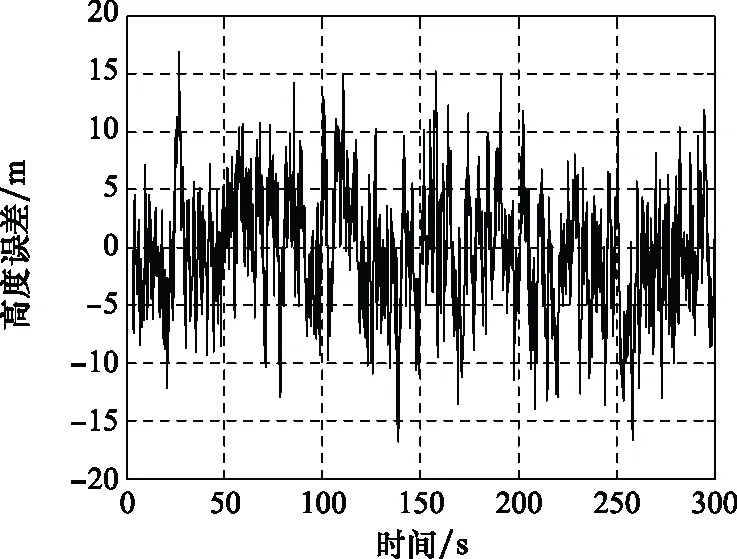
圖21 SINS/GPS組合導航高度誤差曲線Fig.21 SINS/GPS integrated navigation height error curve

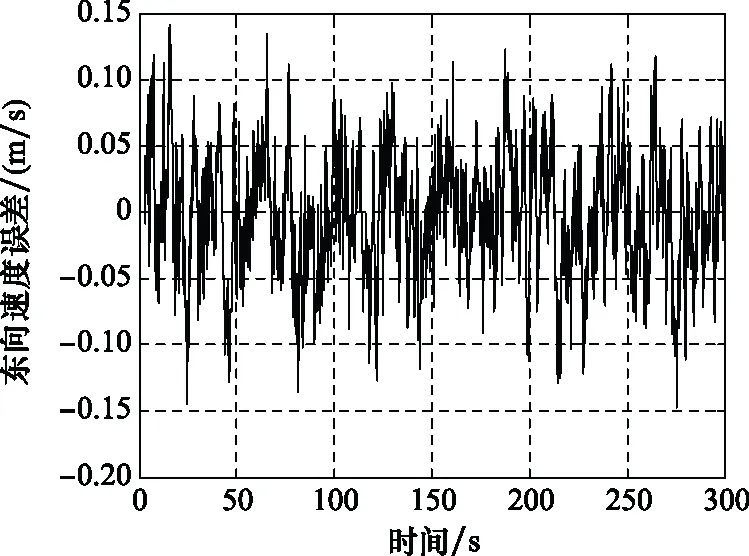
圖22 SINS/GPS組合導航東向速度誤差曲線Fig.22 SINS/GPS integrated navigation east velocity error curve

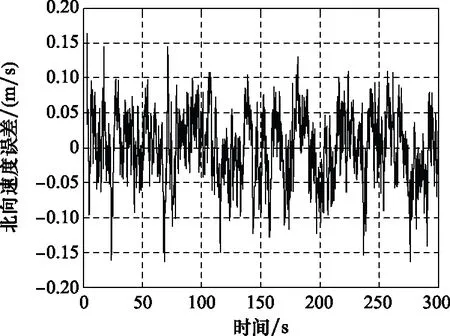
圖23 SINS/GPS組合導航北向速度誤差曲線Fig.23 SINS/GPS integrated navigation north velocity error curve

我們統計了SINS/GPS組合導航進入穩定狀態后的組合導航誤差,如表4所示。

表4 SINS/GPS組合導航精度指標

如表4所示,SINS/GPS組合導航在水平方向以及高度方向的定位誤差均不大于6 m,其雙向測速精度可達到 0.2 m/s以內,俯仰以及滾轉精度均小于 0.8′,其角度以及位置誤差已基本滿足運載器在進近著陸段的定位要求。但相比于單一GPS導航精度(即小于0.1 m)定位導航的要求,SINS/GPS組合導航精度依然存在較大的提高空間。

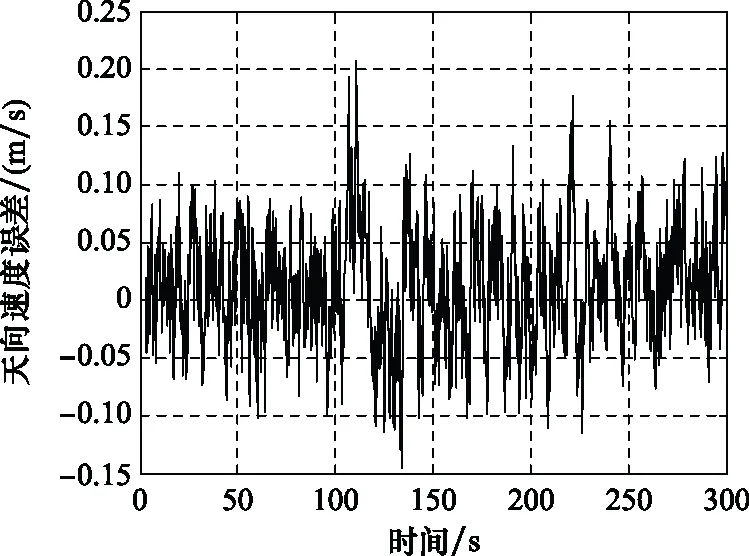
圖24 SINS/GPS組合導航天向速度誤差曲線Fig.24 SINS/GPS integrated navigation up velocity error curve

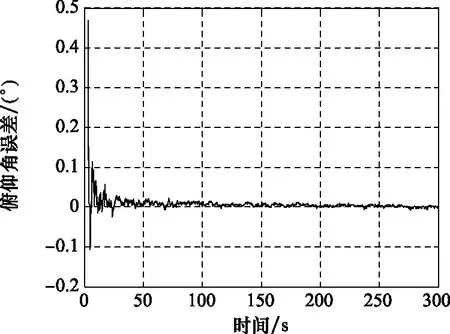
圖25 SINS/GPS組合導航俯仰角誤差曲線Fig.25 SINS/GPS integrated navigation pitch angle error curve

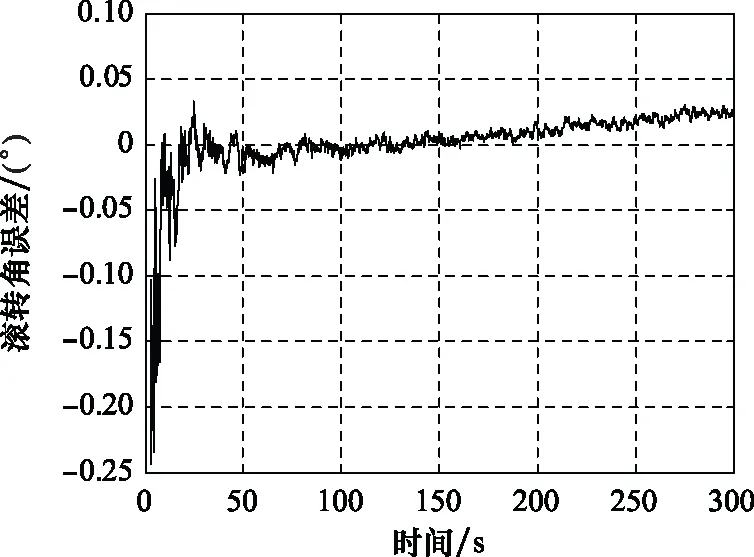
圖26 SINS/GPS組合導航滾轉角誤差曲線Fig.26 SINS/GPS integrated navigation roll angle error curve

3.3.2 進近著陸段SINS/GBAS組合導航仿真結果

通過第3.2節建立的“輸出+反饋”SINS/GBAS組合導航方法,對可重復使用運載器的進著陸段進行數值模擬,計算的導航參數誤差曲線如圖27～圖34所示,并與第3.3.1節的SINS/GPS組合導航的精度指標進行對比。

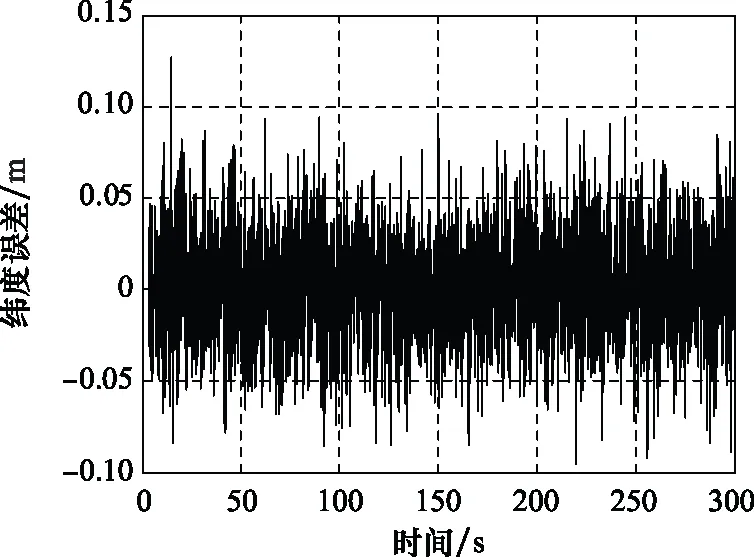
圖27 SINS/GBAS組合導航緯度誤差曲線Fig.27 SINS/GBAS integrated navigation latitude error curve

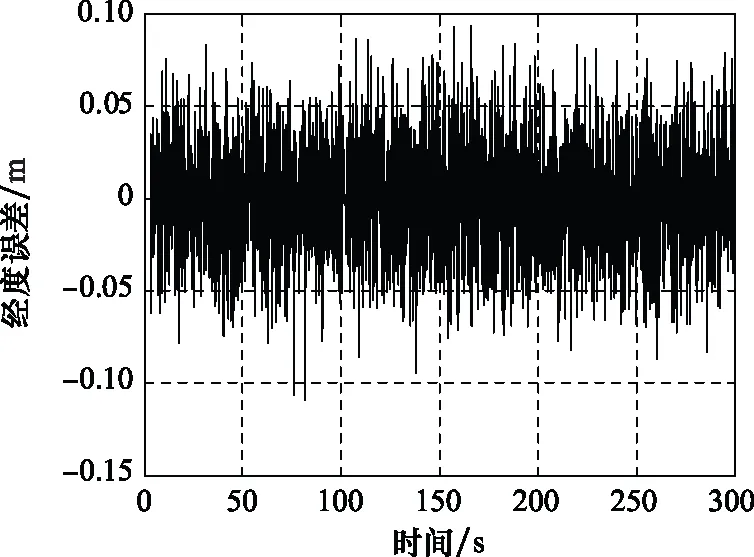
圖28 SINS/GBAS組合導航經度誤差曲線Fig.28 SINS/GBAS integrated navigation longitude error curve

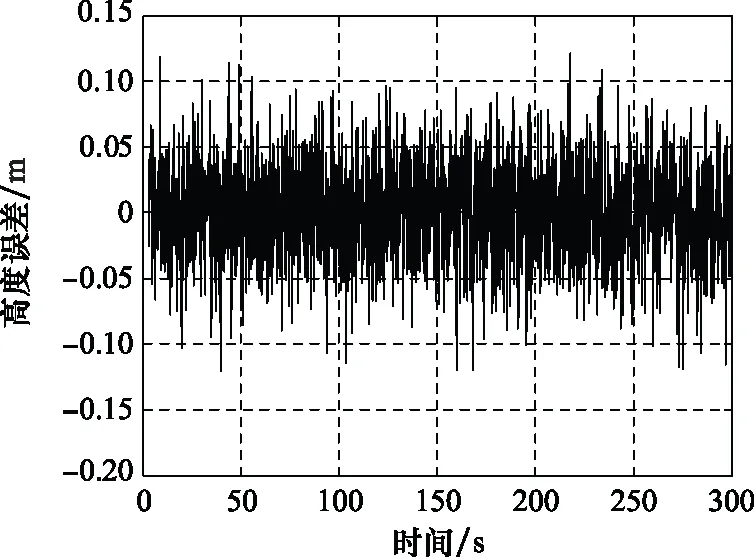
圖29 SINS/GBAS組合導航高度誤差曲線Fig.29 SINS/GBAS integrated navigation height error curve

表5 SINS/GBAS組合導航精度指標

為了與SINS/GPS組合導航精度指標相對比,我們統計了在SINS/GBAS組合導航進入穩定狀態下的3種精度指標,即定位精度、測速精度以及測姿精度。相比SINS/GPS組合導航,SINS/GBAS組合導航的定位以及測速精度明顯有所提高,其水平與高程定位精度小于 0.05 m,測速誤差小于0.04 m/s,均高于SINS/GPS一個數量級。而測姿精度優于3′,與SINS/GPS組合導航相比較差。造成這一現象的主要原因是在進著陸階段航向通道不可觀測,難以對飛行器的測姿精度進行反饋修正。但由于運載器在進近著陸段對測姿精度要求不高,而對定位以及測速精度要求較高,因此相比于SINS/GPS組合導航系統，SINS/GBAS組合導航系統更適用于運載器高精度進近著陸的導航要求。

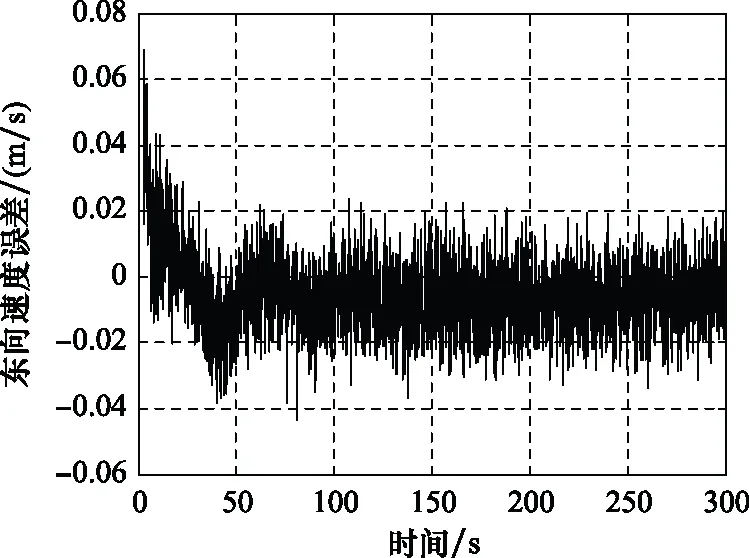
圖30 SINS/GBAS組合導航東向速度誤差曲線Fig.30 SINS/GBAS integrated navigation east velocity error curve

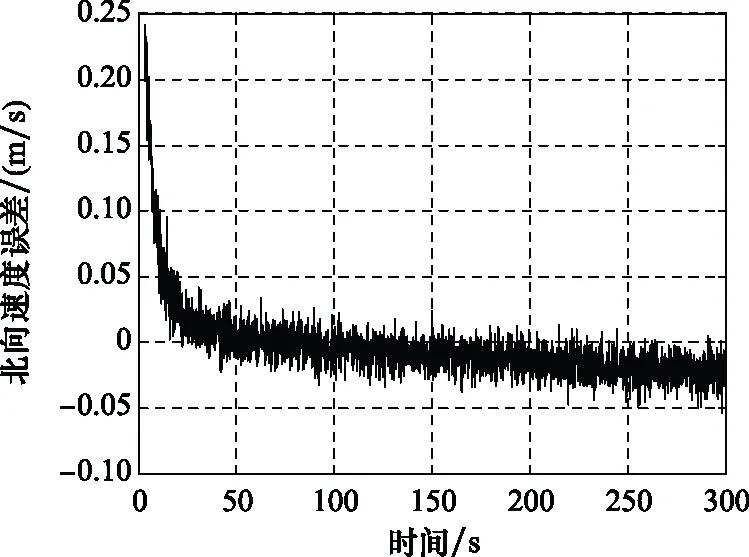
圖31 SINS/GBAS組合導航北向速度誤差曲線Fig.31 SINS/GBAS integrated navigation north velocity error curve

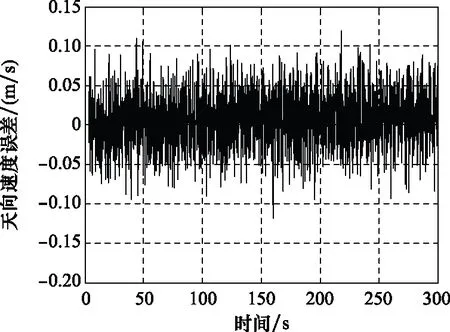
圖32 SINS/GBAS組合導航天向速度誤差曲線Fig.32 SINS/GBAS integrated navigation up velocity error curve

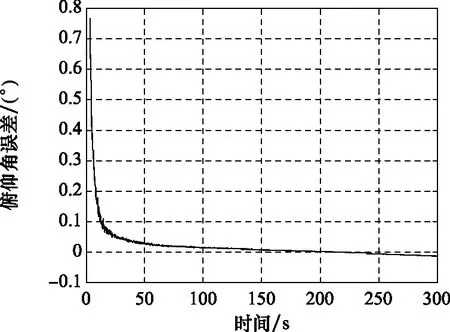
圖33 SINS/GBAS組合導航俯仰角誤差曲線Fig.33 SINS/GBAS integrated navigation pitch angle error curve

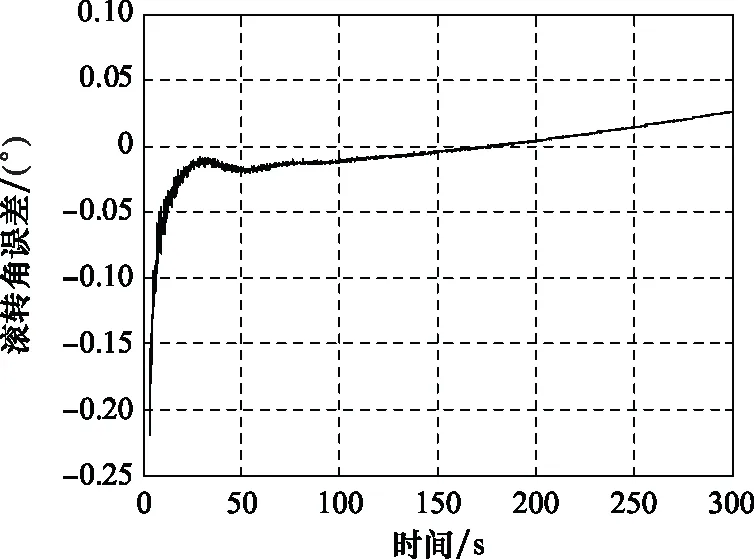
圖34 SINS/GBAS組合導航滾轉角誤差曲線Fig.34 SINS/GBAS integrated navigation roll angle error curve

4 結 論

本文主要研究了SINS/GBAS組合導航方法對于可重復使用運載器在進近著陸段的導航精度以及可行性。相比傳統的衛星導航技術,GBAS通過引入外界條件的影響,特別是對流層誤差的影響,有效地提高了運載器的定位精度，其定位誤差小于0.05 m。此外，通過在系統中加入“輸出+反饋”的輔助導航修正策略,有效地抑制了系統中隨著導航時間延長所引入的非線性誤差,并有效地提高了系統的魯棒性。我們的數值模擬對比了在相同標稱軌跡下,兩種不同的組合導航方式(SINS/GPS與SINS/GBAS)的導航精度,證明了SINS/GBAS組合導航在運載器定位精度、測速精度的優勢所在。為進一步提高可重復使用運載器的可靠性,我們將進一步完善改進GBAS檢測手段,并進一步提高GBAS的故障檢測以及可靠性保證。此外,在某些特殊導航條件下,特別是對于飛行器測姿精度要求較高時,建議采用SINS/GPS和SINS/GBAS組合導航相協作的方法,可有效地提高可重復使用運載器在著陸段的定位精度。