高通量計算二維材料界面摩擦*

崔子純 楊莫涵 阮曉鵬 范曉麗? 周峰3) 劉維民3)

1) (西北工業大學材料學院,先進潤滑與密封材料中心,西安 710072)

2) (西北工業大學,倫敦瑪麗女王大學工程學院,西安 710072)

3) (中國科學院蘭州化學物理研究所,固體潤滑國家重點實驗室,蘭州 730000)

建立了基于第一性原理方法研究二維材料界面摩擦的高通量計算程序,該程序實現了自動化批量建模、批量提交任務、多任務并發計算,以及計算結果自動收集、處理和圖像繪制,使用該程序可以節省時間.采用此程序計算了不同層間距離下雙層氮化硼和雙層石墨烯的滑移勢能面,及層間界面摩擦力和摩擦系數.研究發現,隨著層間距離減小,雙層氮化硼界面的平均摩擦力近似線性增大,摩擦系數為0.11—0.17,雙層石墨烯界面摩擦力先增大后減小再增大,其摩擦系數在12 nN 載荷下達到最小值(0.014),這些結果與已有研究結果一致,驗證了該計算程序的可靠性.此外還研究了表面氫化和氟化對雙層氮化硼界面摩擦的影響,發現氟化氮化硼/氮化硼界面的摩擦系數更低.

1 引言

摩擦一般發生在相對運動或具有相對運動趨勢的接觸界面,阻礙相對運動,同時產生能量損耗.Holmberg 等[1]調查發現卡車等重型交通工具有1/3 的燃料用于克服發動機、變速器的摩擦.為了避免不必要的能源消耗和機器故障,控制摩擦力、黏附力和磨損力以減小摩擦磨損一直是科研工作者密切關注的問題[2].納米尺度下,以黏附和摩擦為代表的表面力成為制約納米機電系統性能和壽命的關鍵因素[3],因此,了解納米級甚至原子尺度下的摩擦行為必要且重要.

因為層間作用力弱、層內共價鍵強、剪切應力較低的特點,層狀二維材料的潤滑性能往往優于其他納米材料[4,5].特別是石墨烯[6]、氮化硼[7]、二硫化鉬[8]等典型二維層狀材料,通常以微米級薄膜的形式被用作固體潤滑劑.已有研究表明,二維材料界面處的原子尺度摩擦行為受到多種因素影響,包括溫度[9?11]、滑動速度[12]以及載荷[12?14]等.研究者采用實驗技術和理論計算方法研究了二維材料界面的原子尺度摩擦行為[15?17].溫度變化會影響表面原子熱振動的幅度以及頻率,從而影響摩擦行為,已有研究顯示摩擦系數隨溫度變化呈現非單調變化的特點[18].摩擦力與滑動速度的關系較為復雜,當滑動速度較小時,摩擦力幾乎不隨速度變化,能量耗散主要來自于黏滑運動,當滑動速度增大到一定程度時,摩擦力與速度呈現線性關系,黏滑運動消失,能耗主要為阻尼能耗[18?20].

依照宏觀摩擦定律,摩擦力與載荷的關系符合阿蒙頓定律,原子尺度上摩擦力與載荷的關系則較為復雜.Mate 等[21]利用鎢探針研究了石墨表面的微觀黏滑現象,發現界面間的平均摩擦力隨法向載荷的增大而近似線性增大;Mo 等[22]采用分子動力學方法模擬了碳尖端在金剛石表面的滑動行為,當接觸界面的范德瓦耳斯吸附力較強時,摩擦力和載荷呈現非線性關系,隨著范德瓦耳斯吸附力的減弱,摩擦力與載荷的關系趨于線性.An 等[23]基于第一性原理方法計算了氮化硼層間摩擦,發現摩擦力隨載荷的增大而增大;Sun 等[24]發現石墨烯層間平均滑移摩擦力隨著載荷增大,先增大后減小再增大的有趣現象.此外,多項研究表明[25?30],層數、表面吸附、面內應變等對石墨烯和氮化硼的層間摩擦有著顯著影響,歸因于層間電子分布的變化.鑒于原子尺度摩擦學的復雜性和重要性,從原子水平上掌握摩擦機制[31],預測和控制摩擦行為緊迫且關鍵.

原子力顯微鏡(atomic force microscope,AFM)研究掃描探針與材料表面之間的摩擦特性,是研究納米尺度摩擦學應用最廣泛的工具.然而,受限于可用作探針尖端的材料種類,AFM 測量任意二維材料界面間摩擦仍然是一個挑戰.先進的計算模擬技術是研究二維材料層間摩擦的有力工具.研究摩擦現象的常用計算模擬方法包括分子動力學模擬(molecular dynamics,MD)方法和基于密度泛函理論(density functional theory,DFT)的第一性原理方法.分子動力學依據牛頓力學定律模擬接觸界面的相對運動,根據公式(U代表原子間相互作用勢,r代表原子的所在位置)求出每個原子的受力,然后分別對所有原子的法向力和與滑動方向相反的橫向力進行求和,得到總的法向力和摩擦力,進而運用阿蒙頓定律求得摩擦系數.分子動力學模擬已被廣泛應用于計算二維材料摩擦學性能[32?35],其模擬的可靠性強烈依賴于選取的勢函數描述層間/內相互作用的準確性.第一性原理計算方法通過計算摩擦界面相對滑動時的能量變化,得到滑動能壘和平均摩擦力,通過改變層間距離模擬外界施加載荷,獲得不同載荷下的勢能面以及摩擦力,再根據阿蒙頓定律求得摩擦系數.該方法可以精確地處理電子結構,并從界面電荷分布探索原子尺度摩擦行為[36?38].

勢能面(potential energy surface,PES)是研究原子尺度摩擦行為的主要途徑[39].特定載荷下的PES 由足夠密集的勢能點組成,對應相應滑移位置處的勢能.構建PES 一般需要建立近700 個滑移位置的界面結構并計算其能量,涉及大量建模、計算、數據處理.本文建立了基于第一性原理方法研究二維材料層間摩擦的高通量計算程序(homogenous/heterogenous junction construction and frictional properties calculation software,HJC2S),該程序自動化建立滑移界面的原子結構,批量建立構建勢能面所需計算的界面構型,高通量計算系列載荷下勢能面上的所有界面結構,自動收集能量并輸出摩擦性能相關數據和圖像.基于該程序計算了雙層氮化硼和雙層石墨烯的界面層間滑移摩擦性能,研究了表面功能化對于氮化硼層間滑移摩擦力的調控.

2 二維材料層間摩擦的高通量計算程序

程序HJC2S 基于Linux 操作系統,所有計算通過基于密度泛函理論[40]的VASP (viennaabinitiosimulation package)軟件包[41?43]完成.程序功能包含了自動化建模、批量產生并提交計算任務、數據提取與存儲(提取并保存數據、繪制并保存圖像) 3 個模塊.如圖1 所示,程序首先基于用戶提供的二維材料結構建立同、異質結界面結構,并對界面結構進行優化;將界面一側的材料沿著z方向按照一定間距移動,模擬系列載荷;特定界面間距下,沿著x,y方向按照一定間距移動界面一側的材料,模擬特定載荷下沿xy平面相對滑移位置;提交對所有界面結構進行自洽計算的任務,通過作業調度系統實現計算資源的有效利用和多任務并發計算,實現二維材料界面摩擦性能的高通量計算;計算完成后,程序智能化處理并輸出計算結果,用戶分析數據以獲得界面的納米摩擦學性能,以下部分介紹具體的計算流程.

圖1 二維材料界面摩擦學特性高通量計算流程示意圖Fig.1.The schematic diagram showing the procedure of high-throughput calculation of the tribological property at the interface of two-dimensional materials.

2.1 構建界面結構

對于異質界面,HJC2S 程序會對提供的兩種二維材料的晶胞矢量進行匹配(本文設置晶格常數失配率不超過5%,失配角不大于3°),構建異質界面結構.程序會提供各種可能晶格矢量的界面結構及該結構中界面兩側的原子數和總原子數,以供用戶挑選合適的界面模型.

2.2 模擬外加載荷

HJC2S 程序通過改變界面間距模擬外加載荷,平衡間距對應零載荷.首先以平衡間距的界面結構為初始結構,設定步長并逐步減小間距,生成系列間距界面結構并對每個間距界面結構建立文件夾.然后批量提交計算系列間距界面結構的任務,并計算系列間距下界面結合能Eb.計算完成后,程序會自動提取并保存結合能以及界面間距的數據,進行數據處理并獲得界面結合能隨界面距離z變化的關系,通過公式求解外加載荷和界面間距之間的對應關系,自動繪制結合能隨界面間距、載荷隨界面間距變化的曲線圖.

2.3 計算不同層間距離的勢能面

HJC2S 程序通過固定界面一側材料,使另一側材料在xy平面做相對橫向滑移來模擬界面相對滑動過程.界面被劃分為M×N的網格(網格點數根據x,y方向長度設定),每一個格點位置對應相對滑移中的一個界面結構.格點劃分的致密程度決定著勢能面計算的精度.為了獲得系列層間距下的勢能面,對每一個層間距離建立文件夾,每個文件夾下有M×N個子文件夾,對應不同的滑移位置.計算完成后,程序會提取每個結構對應的滑移位置坐標和能量數據,保存并以此繪制系列層間距離下的勢能面.

2.4 尋找最小能量路徑

HJC2S 程序依據計算得到的勢能面和最小能量路徑起點和終點,采用String 方法[44]在勢能面上尋找最小能量路徑.String 方法是一種優秀的過渡態搜索算法,該方法以提供的起點和終點為初始值,確定兩個勢能極小值,然后采樣多條連接兩個能量極小值的曲線,通過構造曲線微分方程,使曲線逐漸逼近最小能量路徑.確定最小能量路徑后提取并輸出路徑位置坐標及能量,繪制最小能量路徑及其上的靜橫向力曲線.

2.5 計算平均摩擦力

HJC2S 程序將篩出特定載荷下勢能面上的極值點,選取鄰近的最大值點和最小值點,通過兩點的坐標以及能量,根據公式計算得到界面平均摩擦力,其中 ?V=Vmax?Vmin(Vmax為勢能極大值,Vmin是勢能極小值),?x是Vmax和Vmin所在位置之間的距離.程序自動計算系列外加載荷下的界面平均摩擦力〈Ff〉,輸出外加載荷-平均摩擦力的對應數據并繪制外加載荷與界面平均摩擦力關系曲線.

3 計算方法

3.1 程序中涉及物理量的計算

HJC2S 程序采用如下公式計算界面結合能Eb:

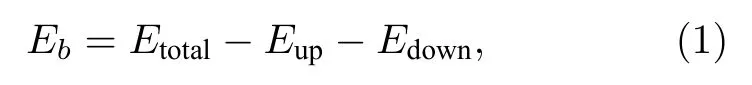
其中,Etotal是特定層間距下滑移界面的總能量,Eup,Edown分別是界面兩側材料的能量.外加載荷Fn與結合能Eb之間滿足關系[45]:

程序由(1)式計算系列間距下界面結合能,由(2)式得到法向載荷與層間距的關系.

勢能的計算公式如下:

其中V(x,y,Fn)和Eb(x,y,Fn)為Fn載荷下、(x,y)位置處的勢能和界面結合能,z(x,y,Fn)為Fn載荷對應的界面間距,Fnz(x,y,Fn)為抵抗外加載荷Fn所做的功,V0(Fn)是Fn載荷下勢能面上的最小勢能點,其計算公式如下:

Eb(x0,y0,z(x0,y0,Fn))為零勢能位置滑移體系的界面結合能,Fnz(x0,y0,Fn) 為零勢能位置處抵抗外加載荷Fn的層間作用能,(x0,y0)為Fn載荷下零勢能位置坐標.

特定載荷下界面平均摩擦力〈Ff〉由如下公式[45]計算:

其中?V表示該載荷下最大滑移能壘,由勢能最大值與最小值決定

?x表示勢能最大值點與最小值點之間的距離.摩擦系數μ與平均摩擦力和載荷之間的關系為

3.2 本文采用的計算方法和設置

文章所有計算均采用基于密度泛函理論[40]的VASP 程序包[41?43]進行.采用廣義梯度近似(general gradient approximate,GGA)的Perdew-Burke-Ernzerhof(PBE)[46]方法計算電子交換關聯能,采用平面投影綴加波贗勢(projector augmented wave,PAW)方法[47]描述電子和離子之間相互作用,采用范德瓦耳斯色散修正方法(density functional dispersion correction)DFT-D3 描述相鄰層之間的范德瓦耳斯弱相互作用.在倒易空間中,電子波函數通過平面波基組擴展,平面波基組截斷能設定為550 eV,能量和力的收斂精度分別設置為10–5eV和0.02 eV/?.在總能計算過程中,不弛豫原子位置.布里淵區K點網格取樣采用Gamma 方法,K網格大小根據具體模型由Vaspkit[48]生成.為了消除z方向上周期性結構之間的相互作用,沿垂直方向添加了20 ?厚度的真空層.

4 結果與討論

本文采用HJC2S 程序計算了雙層氮化硼(BN/BN)、雙層石墨烯(Gr/Gr)、氫化氮化硼/氮化硼(H-BN/BN)和氟化氮化硼/氮化硼(F-BN/BN)的層間滑移摩擦行為.為了模擬不同載荷下的層間滑移摩擦行為,將兩層之間層間距以步長0.1 ?逐步壓縮,研究了層間距離為4.0—1.5 ?的Gr/Gr 和層間距離為4.0—2.5 ?的BN/BN,H-BN/BN 和F-BN/BN 的勢能面、界面摩擦力和摩擦系數.

4.1 不同載荷下雙層氮化硼界面摩擦力

首先研究了BN/BN 的界面摩擦行為,測試HJC2S 程序的可靠性.圖2(a),(b)分別為BN/BN處于Top(T)位置和Hollow(H)位置的俯視圖和側視圖.Top 位置結合能為29 meV/atom,層間距為3.39 ?,與Marom 等[49]采用PBE+Vdw 方法計算得到的BN/BN 界面層間距(3.37 ?)吻合.采用2×2 超胞模擬BN/BN 界面層間相對滑移,將Top 位置設置為初始位置,沿著xy平面滑動距離設置為5 ? × 5 ?,用于構建勢能面的網格大小為0.2 ? × 0.2 ?,第一布里淵區K網格大小設為7 × 7 × 1.

圖2 BN/BN,H-BN/BN 和 F-BN/BN 雙層體系原子結構的俯視圖和側視圖 (a) Top 和(b) Hollow 位置BN/BN 的俯視圖和側視圖;(c) H-BN/BN 和(d) F-BN/BN 在Hollow 位置的俯視圖和側視圖Fig.2.Top and side views for atomic structures of BN/BN,H-BN/BN,and F-BN/BN bilayer.Top and side views of BN/BN bilayer in (a) Top and (b) Hollow positions.Top and side views of (c) H-BN/BN and (d) F-BN/BN bilayers in Hollow position.

界面結合能與層間距的關系是計算中最重要的一部分,該曲線擬合的精確度決定著計算結果的準確度.圖3(a)展示了Top 位置的BN/BN 界面結合能隨層間距的變化.隨著層間距縮小,界面結合能逐漸變小,當層間引力達到最大值時,界面結合能達到最小值;之后,界面結合能開始增大,當界面結合能為0 eV 時,引力和斥力達到平衡;之后,斥力在層間作用中起主導作用.通過改變BN/BN 層間距來模擬載荷,根據 (2)式得到載荷與層間距的關系.如圖3(b)所示,隨著BN/BN 層間距減小,載荷不斷增大.

圖3 BN/BN 位于Top 位置的界面結合能和載荷隨層間距的變化 (a) 結合能;(b) 載荷Fig.3.The variation of interlayer binding energy (Eb) and load with interlayer distance for BN/BN bilayer at Top position: (a) Eb and (b) load.

圖4(a)—(i)為0—8 nN 載荷下BN/BN 沿著xy平面分布的勢能.由于BN/BN 結構本身的周期性,所以勢能也呈現周期性分布.如圖4 所示,0 nN 載荷下,BN/BN 的勢能面比較平滑,Top 位置處勢能最大,Hollow 位置處勢能最小.這是因為,相較于Hollow 位置,Top 位置的正對原子更多,層間相互作用更強.隨著載荷增大,抵抗負載的層間作用增大,勢能面起伏逐漸增大,能壘也逐漸增大,勢能最大值和最小值對應的位置并未發生變化.高勢能起伏增大了滑移阻力及因摩擦耗散的能量,根據(5)式,平均摩擦力也在逐漸增大.

圖4 顯示了各載荷下的最小能量路徑(勢能面上連接勢能最小值點的路徑中勢能起伏最小的路徑),圖5 為0—8 nN 載荷下最小能量路徑上的能量變化曲線.從圖5 可以看出,由于結構的對稱性,能量隨位移變化也具有周期性.沿最小能量路徑進行滑移時,勢能先增大后減小,然后再重復此過程.另外,隨著載荷的增大,最小能量路徑上的能壘逐漸增大,即界面滑移的阻力增大,從而導致更高的摩擦.

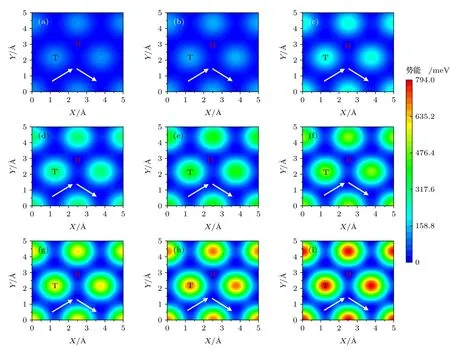
圖4 不 同載 荷下BN/BN 的勢 能面 (a) 0 nN;(b) 1 nN;(c) 2 nN;(d) 3 nN;(e) 4 nN;(f) 5 nN;(g) 6 nN;(h) 7 nN;(i) 8 nN.T 和H 分別表示Top 和Hollow 位置,白色帶箭頭線代表最小能量路徑Fig.4.Potential energy surface of BN/BN bilayer under normal load of (a) 0 nN,(b) 1 nN,(c) 2 nN,(d) 3 nN,(e) 4 nN,(f) 5 nN,(g) 6 nN,(h) 7 nN and (i) 8 nN.T and H present the Top and Hollow positions,respectively.The white lines with arrow represent the minimum energy path.

圖5 0—8 nN 載荷下BN/BN 最小能量路徑上勢能的變化Fig.5.The variation of potential energy along the minimum energy path of BN/BN bilayer under 0–8 nN loads.

從圖6(a)可以看出,隨著載荷增大,BN/BN界面的平均摩擦力近似線性增大,表現出類阿蒙頓定律的特征,表明宏觀摩擦力與載荷之間的關系擴展到了納米尺度的BN/BN 滑移界面.從圖6(b)可以看出,當載荷從1 nN 增大到8 nN 時,BN/BN滑移界面的摩擦系數從0.17 降至0.11.因表面結構、環境、計算方法等不同,測得的六方氮化硼界面的摩擦系數為0.025—0.7.Martin 等[50]發現超高真空下h-BN 與h-BN 界面的摩擦系數為0.7,而在潮濕空氣中的摩擦系數為0.1.Wang 等[51]指出h-BN 固體潤滑劑的適用溫度范圍為–184—538 ℃,相應的摩擦系數為0.1—0.2.An 等[23]采用DFTLDA 泛函描述BN/BN 界面的相互作用,研究了BN/BN 界面摩擦系數與載荷的變化關系,他們指出,當載荷從1 nN 增大到5 nN 時,沿著x方向滑移摩擦系數從0.1 下降至0.025,在5—10 nN 載荷下,摩擦系數從0.025 上升到0.13.本文研究了不同載荷下BN/BN 的勢能面與摩擦力,摩擦系數計算結果與已有研究結果一致.

圖6 BN/BN,F-BN/BN,H-BN/BN 的平均界面摩擦力(Ff)和摩擦系數(μ)隨載荷的變化 (a)平均摩擦力;(b)摩擦系數Fig.6.The variation of friction force at the interface of BN/BN,F-BN/BN,and H-BN/BN bilayers with respect to the normal load: (a) Averaged interfacial friction (Ff);(b) friction coefficient (μ).

4.2 不同載荷下雙層石墨烯界面摩擦力

以0.1 ?步長將層間距離從4 ?壓縮到1.5 ?,計算了系列層間距下雙層石墨烯(上下層均為2 個原子)之間的結合能,得到結合能隨層間距變化的關系,根據(2)式得到載荷與層間距的關系,以此模擬0—13.5 nN 外加載荷.將沿xy平面滑動距離設置為2.6 ? × 2.6 ?,網格大小設為0.2 ? × 0.2 ?,第一布里淵區K網格設為12 × 12 × 1.計算了1—13.5 nN 外加載荷下Gr/Gr 的勢能面,結果如圖7 所示.從圖7 可以發現,當外加載荷為1 nN時,勢能面較為平坦,Top 位置勢能最高,Hollow位置勢能最低.隨著載荷升高,勢能最大值先增大后減小.當載荷達到12 nN 時,勢能面發生了反轉,即原來高勢能點(Top 位置)變為低勢能點,低勢能點(Hollow 位置)變為高勢能點,勢能面趨于平坦,能壘很低.隨著載荷的進一步增大,勢能起伏再次逐漸增大.

圖7 不同載荷下Gr/Gr 的勢能面 (a) 1 nN;(b) 4 nN;(c) 7 nN;(d) 10 nN;(e) 12 nN;(f) 13.5 nN.(a)—(d)中的H/T 對應最小/最大勢能,而(e),(f)中的H/T 對應最大/最小勢能Fig.7.Potential energy surface of graphene/graphene (Gr/Gr) bilayer under normal load of (a) 1 nN,(b) 4 nN,(c) 7 nN,(d) 10 nN,(e) 12 nN,and (f) 13.5 nN.T and H present the top and hollow positions,respectively.H/T in (a)–(d) is the position of minimum/maximum potential energy,whereas,T/H in (e),(f) is the position of minimum/maximum potential energy.

在勢能計算的基礎上,計算了1.0—13.5 nN外加載荷下Gr/Gr 界面的平均摩擦力和摩擦系數.圖8(a)所示為平均摩擦力隨載荷的變化曲線.如圖所示,隨著載荷升高,Gr/Gr 界面的平均摩擦力逐漸增大;當載荷增大到10 nN 時,平均摩擦力開始下降,直到載荷為12 nN 時,平均摩擦力達到極小值;之后,平均摩擦力隨著載荷的增大再次逐漸增高.圖8(b)所示為1.0—13.5 nN 外加載荷下Gr/Gr 的界面摩擦系數.從圖中可以看出,隨著載荷的升高,摩擦系數先減小后增大.當載荷為12 nN 時,摩擦系數最小(0.014),這是因為12 nN 下的勢能面最平坦,界面滑移需要克服的能壘最低,表現出極低的摩擦系數.

圖8 Gr/Gr 界面平均摩擦力和摩擦系數隨載荷的變化 (a)平均摩擦力;(b)摩擦系數Fig.8.The variation of friction force at the interface of graphene/graphene (Gr/Gr) bilayers with respect to the normal load:(a) Averaged interfacial friction and (b) friction coefficient.

本文計算的摩擦力隨載荷變化的趨勢成功復現了Sun 等[24]的研究結果.此外,最小摩擦系數出現的層間距為1.75 ?,與Zhang 等[52]得出的極低摩擦現象發生的層間距(1.78 ?)相近,與Sun 等[24]得出的極低摩擦現象發生的層間距(1.825 ?)略有差距,這是因為Sun 等[24]是通過固定部分原子方法計算總能,而本文采用了固定所有原子的方法計算總能,本文計算方法可以節省計算資源并減少計算時間.Fan 等[53]在實驗中測得的石墨烯的摩擦系數為0.1—0.2,Wang 等[27]計算結果顯示,載荷為1—9 nN 時石墨烯界面的摩擦系數為0.05—0.225.本文計算顯示石墨烯界面摩擦系數為0.014—0.14,與文獻[53]計算結果一致.這些均證明了HJC2S 程序和其采用算法研究界面摩擦行為的可靠性.

4.3 表面改性調控BN/BN 界面摩擦力

圖2(c),(d)分別為H—BN/BN 和F—BN/BN的俯視圖與側視圖.H—BN 和F—BN 中B—H,N—H,B—F,N—F 鍵長分別為1.20,1.03,1.36,1.44 ?.H—BN/BN 和F—BN/BN 位于Top 位置平衡結構的層間距分別為2.91 ?和3.20 ?,xy平面晶格常數為2.54 ? 和 2.57 ?.采用HJC2S程序,構建了勢能面網格,大小均為5 ? × 5 ?,網格尺寸為0.2 ? × 0.2 ?,計算了0—8 nN 載荷下H—BN/BN 和F—BN/BN 的勢能面及界面平均摩擦力和摩擦系數.

圖6(a)為BN/BN,F—BN/BN 和H—BN/BN滑移界面平均摩擦力隨載荷變化的曲線,如圖所示,1—8 nN 載荷下,3 種滑移界面平均摩擦力均隨載荷增大而增大.圖6(b)所示為3 種滑移界面摩擦系數隨載荷變化的曲線.隨著載荷增大,H—BN/BN 界面摩擦系數增大,F—BN/BN 界面摩擦系數先減小后緩慢升高,摩擦系數值為0.08—0.10.當載荷小于6 nN 時,H—BN/BN 滑移界面的摩擦系數小于BN/BN 滑移界面的摩擦系數;當載荷大于6 nN 時,H—BN/BN 滑移界面的摩擦系數大于BN/BN 滑移界面的摩擦系數.可以明顯地看出F—BN/BN 滑移界面的平均摩擦力和摩擦系數均小于BN/BN 和H—BN/BN,表明表面氟化顯著降低了摩擦.

電荷轉移是影響摩擦力的主要因素[54?56],為了探析氟化降低BN 界面摩擦的內在原因,計算了BN/BN 以及F-BN/BN 的電荷分布.圖9為0 nN和8 nN載荷下BN/BN 和F-BN/BN在勢能最高位置和最低位置處的差分電荷密度圖.由于F 原子的電負性較強,F-BN/BN 層間電子聚集在F 原子附近,層間電荷轉移較小;BN/BN 層內電子結合能力較弱,層間電荷轉移較為明顯.從圖9可以看出,0 nN 和8 nN 載荷下,BN/BN 由Top位置(勢能最大值點)滑移到Hollow 位置(勢能最小值點)時,電荷分布變化顯著.氟化后BN 界面從高勢能點滑移到低勢能點位置時,電荷分布無明顯變化,所以滑移過程中的能壘較低,層間摩擦小,因此降低了BN 界面摩擦.

圖9 BN/BN 和F-BN/BN 的最高和最低勢能態在0 nN 和8 nN 載荷下的差分電荷密度 (a) BN/BN,0 nN;(b) BN/BN,8 nN;(c) F-BN/BN,0 nN;(d) F-BN/BN,8 nN.黃色代表電子聚集,藍色代表電子損失;左邊和右邊的圖分別對應最高和最低勢能態;圖(a)和(c)中的等值面設置為0.00006e/Bohr3;圖 (b) 和 (d) 中的等值面設置為0.0003e/Bohr3Fig.9.Differential charge density of BN/BN and F-BN/BN bilayer at the highest and lowest potential energy state under 0 nN and 8 nN loads.BN/BN bilayer under (a) 0 nN and (b) 8 nN load,F-BN/BN bilayer under (c) 0 nN and (d) 8 nN loads.The yellow color represents electron aggregation,and the blue color represents electron dissipation.The isosurface value in figure (a) and (c) is set to 0.00006e/Bohr3;the isosurface value in figure (b) and (d) is set to 0.0003e/Bohr3.

4.4 方法的適用性與局限性

DFT 方法可以深入到量子尺度,從電子分布的角度解釋摩擦現象.盡管該方法已經被廣泛的用來預測層間滑移的摩擦系數,但該方法仍存在一些局限性.首先,在層間相對滑動的過程中,本文將上下層均設為剛性,并未考慮層間彎曲的影響.其次,本文通過改變計算體系的堆疊構型以模擬層間滑動,因此計算得到的實際結果本質是靜摩擦,而非動摩擦.另外,DFT 計算本身具有局限性,如在計算過程中無法直接引入溫度,因此該方法并未考慮溫度的影響;計算通常是對數十個原子進行,無法對幾百個原子進行計算.

5 結論

報道了一個基于第一性原理方法計算二維材料層間滑移摩擦行為的高通量、自動化計算程序.該程序實現了同、異質結界面自動化建模、計算任務自動生成及提交、智能提取并存儲計算結果、自動處理數據并計算摩擦力和摩擦系數,極大地縮短了建模和處理數據的時間.采用此程序模擬計算了外加載荷下雙層氮化硼層間滑移的摩擦,得到的摩擦系數與實驗和已有計算結果一致,同時研究了雙層石墨烯層間滑移的摩擦力和摩擦系數,計算結果與文獻結果相吻合,證明了該程序計算結果的可靠性.此外,我們研究了表面改性對雙層氮化硼層間滑移摩擦的影響,結果表明表面氟化可以很好地降低摩擦,提供了降低六方氮化硼界面摩擦的表面改性方法.